正负序电流环对柔直系统交流阻抗波动特性影响机理分析

尹太元，王 跃，王晓雷，刘 普，李风漠，孙 杰

（1. 电力设备电气绝缘国家重点实验室（西安交通大学）,陕西省西安市 710049；2. 中原工学院电子信息学院,河南省郑州市 450007；3. 郑州轻工业大学电气信息工程学院,河南省郑州市 450002）

0 引言

近年来,基于模块化多电平换流器的柔性直流输 电（modular multilevel converter based high voltage direct current transmission,MMC-HVDC）系统在直流输电领域得到了广泛应用［1-6］。目前,在柔性直流（简称柔直）输电领域,中国已建成上海南汇工程、舟山工程、渝鄂背靠背柔直工程,以及张北柔直电网等多个工程,无论是在工程数量方面还是电压等级方面,中国均达到了国际一流水平。为了稳步实现“碳中和”这一宏伟目标,中国将会进一步加强海上风电等绿色能源的应用,MMC-HVDC 系统也将迎来更加广阔的应用前景。

随着柔直输电工程的增多,在工程调试阶段以及实际运行期间,发生了多起柔直系统振荡失稳现象,如鲁西柔直工程以及渝鄂柔直工程在调试阶段均发生过系统振荡现象［7-8］,这一现象引起了工业界和学界的广泛关注。振荡现象不仅降低了系统运行的可靠性,而且增加了电气设备损坏的风险。针对柔直工程的振荡现象,其振荡机理、相关影响因素以及振荡抑制策略均成为柔直工程领域的研究热点。

基于端口阻抗的稳定性分析方法在多个实际工程中得到了应用［9-12］,其在柔直工程振荡现象分析中的有效性得到了实际验证,其中模块化多电平换流器（modular multilevel converter,MMC）的端口阻抗模型是应用该分析方法的基础。目前,在MMC的阻抗模型建模方面已经取得了一些研究成果。文献［13］考虑MMC 内部谐波动态,基于多谐波线性化方法建立了MMC 的交流侧序阻抗模型。文献［14］将谐波状态空间理论应用于MMC,考虑了MMC 的内部动态特性,建立了高精度的MMC 阻抗模型。随着柔直系统振荡现象的增多,关于MMC阻抗模型的研究也越来越细化,更多影响阻抗特性的因素被深入研究。文献［15-16］指出,系统的链路延时将会导致MMC 阻抗在中高频段存在负阻尼区域,存在引发系统高频振荡的风险。文献［17］在MMC 阻抗建模过程中考虑了电压前馈环节,指出电压前馈对不同控制模式下的MMC 阻抗均会有影响,存在恶化系统稳定性的风险。

在实际的柔直工程中,正负序电流控制环和正负序分离算法是MMC 控制系统中必不可少的一部分,主要功能是实现电气量的正负序分离,对于短路故障穿越等场景具有重要意义［18］。目前,工程现场对MMC 换流站的阻抗扫描结果显示,当考虑正负序电流控制环和序分离环节时,MMC 的阻抗存在周期性波动现象,该阻抗波动现象在忽略正负序分离环节和负序电流控制后消失,降低了柔直系统稳定性,增加了系统振荡风险,有必要进一步深入研究。但是,目前很少有文献在阻抗建模过程中充分考虑正负序电流控制环和正负序分离环节,详细分析正负序电流控制环和序分离环节对MMC 阻抗特性以及系统稳定性的影响。文献［19］在建模过程中考虑了序分离环节的影响,但没有给出序分离环节传递函数的详细推导过程,也没有进一步分析序分离环节对系统稳定性的影响。文献［20］建立了包含正负序电流控制环和序分离环节的MMC 阻抗模型,并且指出当正负序电流环控制器参数不一致时,MMC 交流阻抗的波动会加剧,但其没有进一步从理论上解释这一现象。

鉴于此,本文在文献［20］的基础上,在对称电网系统下,基于多谐波线性化方法,在考虑正负序分离算法环节以及正负序电流控制环的前提下,建立了MMC 的交流端口详细阻抗模型。在详细阻抗模型的基础上,推导了交流阻抗的简化模型,验证了该简化模型足以分析阻抗波动现象的合理性,并利用该简化模型从理论上分析了交流阻抗波动现象的产生机理。针对交流阻抗波动现象会随着正负序电流环控制器参数的不一致性增加而波动进一步加剧这一现象,基于该阻抗简化模型,从理论上阐述了该现象的影响机制。最后,实验验证了上述理论分析的正确性。

相较于文献［20］,本文的贡献主要集中在以下几点:1）建立了适用于分析MMC 交流阻抗波动现象的简化模型,有利于从理论上分析考虑正负序电流控制环和正负序分离算法时的MMC 阻抗波动的产生机理；2）从理论上阐述了交流阻抗波动的产生机理,以及阻抗波动会随着正负序电流环控制器参数不一致性的增加而进一步加剧的机理。

1 正负序分离环节的数学模型

MMC 的子模块数量众多且控制结构较为复杂,其控制系统一般包含极控部分和阀控部分,其控制系统的整体框图如附录A 图A1 所示,主要包括正负序分离环节、控制外环、正序电流内环、负序电流内环、环流抑制环节以及锁相环等。本文的研究重点之一是正负序分离环节。目前的正负序分离算法有多种,其中延时对消法是一种较为常用的正负序分离算法［21］,本文主要针对该方法进行研究,其他种类的序分离算法将会在后续工作中进一步研究。基于延时对消法的正负序分离算法的控制结构如附录A 图A2 所示。该结构由正序通道和负序通道共同组成,将包含正负序分量的电流进行abc/αβ坐标变换,坐标变换后进行1/4 个工频周期延时（5 ms）,在完成相应变量的求和运算后,进行坐标反变换,从而获取相应的正负序变量［22］。这种基于延时对消法的序分离算法对基频分量有着较好的序分离作用,如果输入的是基频电流,则正序分量将通过正序通道流出、负序分量将通过负序通道流出,但当电流分量中包含除基频以外的分量时,该分量将同时通过正序通道和负序通道,正负序分量无法完全分离。

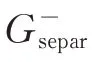
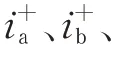
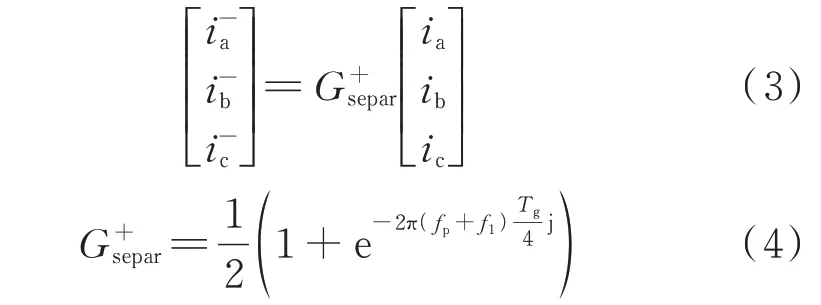
当序分离环节的输入为负序谐波电流时,正序通道和负序通道的输出与序分离环节输入的关系分别为［20］:

上述序分离环节的数学模型［20］为MMC 阻抗模型的推导奠定了理论基础。

2 MMC 的详细阻抗模型

基于多谐波线性化,在考虑正负序电流控制环和正负序分离环节的基础上,建立MMC 阻抗模型［20］。

2.1 MMC 电气部分小信号模型

MMC 的结构如附录A 图A3 所示。图中,MMC包含6 个桥臂,每个桥臂包含n个子模块和1 个桥臂电感,SMi（i=1,2,…,n）表示各桥臂第i个子模块；每个电气变量包含2 个下标,分别代表各相（a、b、c）和上下桥臂（u 代表上桥臂、l 代表下桥臂）,L代表桥臂电感,桥臂电感的寄生电阻为rL,Cm代表子模块电容值。

利用谐波线性化方法,得到MMC 的结构框图如附录A 图A3 所示。首先,在MMC 交流端口注入频率为fp的正弦扰动电压［13-14］,MMC 的a 相端口电压表示为:

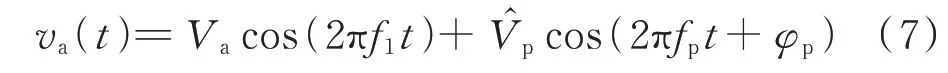
式中:Va为a 相电网电压的幅值；和φp分别为所注入扰动电压的幅值和相位。根据注入扰动电压的正负序特性相位,b 相和c 相分别滞后或超前2π/3。

根据MMC 的三相对称性,以a 相为例,基于多谐波线性化理论,其电气部分的小信号模型为［23-24］:

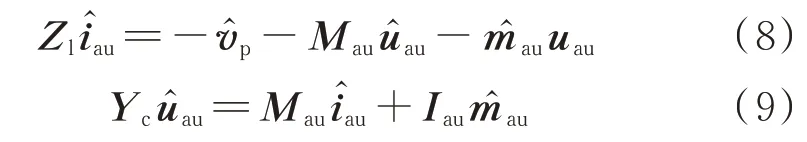
综合考虑建模的精度要求以及数学运算的复杂性,本文中MMC 谐波取到3 次［26］。各谐波的正负序关系以及差模共模关系如附录A 表A1 所示［13］。

2.2 MMC 控制系统小信号模型

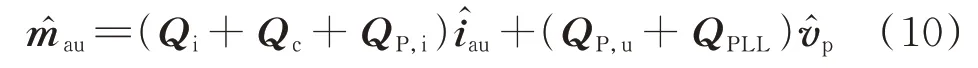
式中:Qi、Qc、QP,i、QP,u和QPLL分别为电流内环控制、环流抑制环路、功率外环的电流控制、功率外环的电压控制和锁相环部分的系数矩阵。本文谐波频率取到3 次谐波,故上述控制环路系数矩阵均为7 阶矩阵。

当MMC 端口注入正序谐波电压扰动时,各控制环路的系数矩阵的具体推导过程如下文所示。当注入的电压扰动为负序时与该推导过程类似,本文不再赘述。

2.2.1 考虑序分离环节的电流内环控制

当考虑序分离环节时,电流内环的系数矩阵Qi可以表示为:

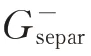
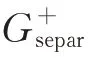
2.2.2 环流抑制环路

环流抑制环路的系数矩阵已在文献［27］中推导,其结果为:

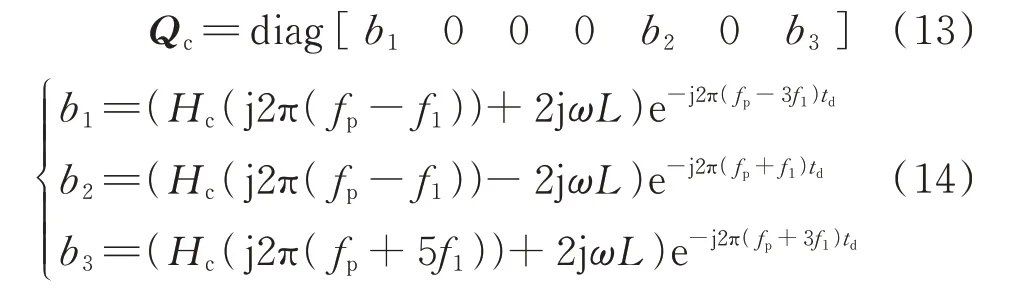
式中:b1、b2和b3分别为对应谐波频率fp-3f1、fp+f1和fp+3f1的控制系数；Hc（·）为环流抑制控制器的传递函数。

2.2.3 功率外环控制

功率外环的电流控制部分也会受到序分离环节的影响。充分考虑序分离环节的影响,功率外环的电流控制部分的系数矩阵可以表示为:

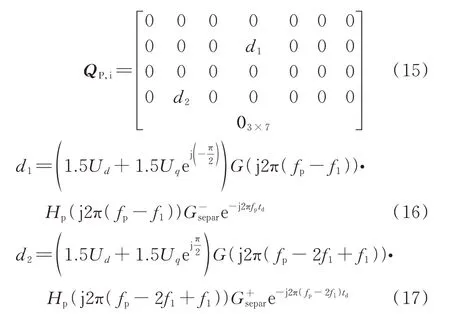
式中:Ud和Uq为MMC 交流侧电压稳态值在dq轴下的形式；d1为频率为fp的差模正序电流在功率外环中对调制波的影响；d2为频率为fp-2f1的差模负序电流在功率外环中对调制波的影响；G（·）为功率外环的传递函数。

功率外环中的电压控制部分的系数矩阵可以表示为:

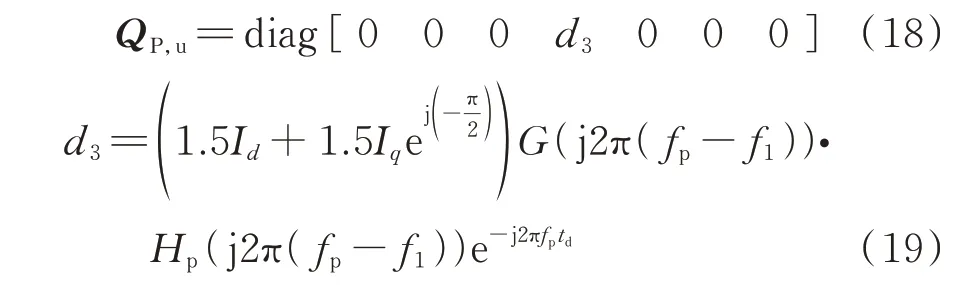
式中:Id和Iq为MMC 稳态电流在dq轴下的形式。

2.2.4 锁相环

在考虑序分离环节的影响后,锁相环的系数矩阵可以表示为［20,27］:

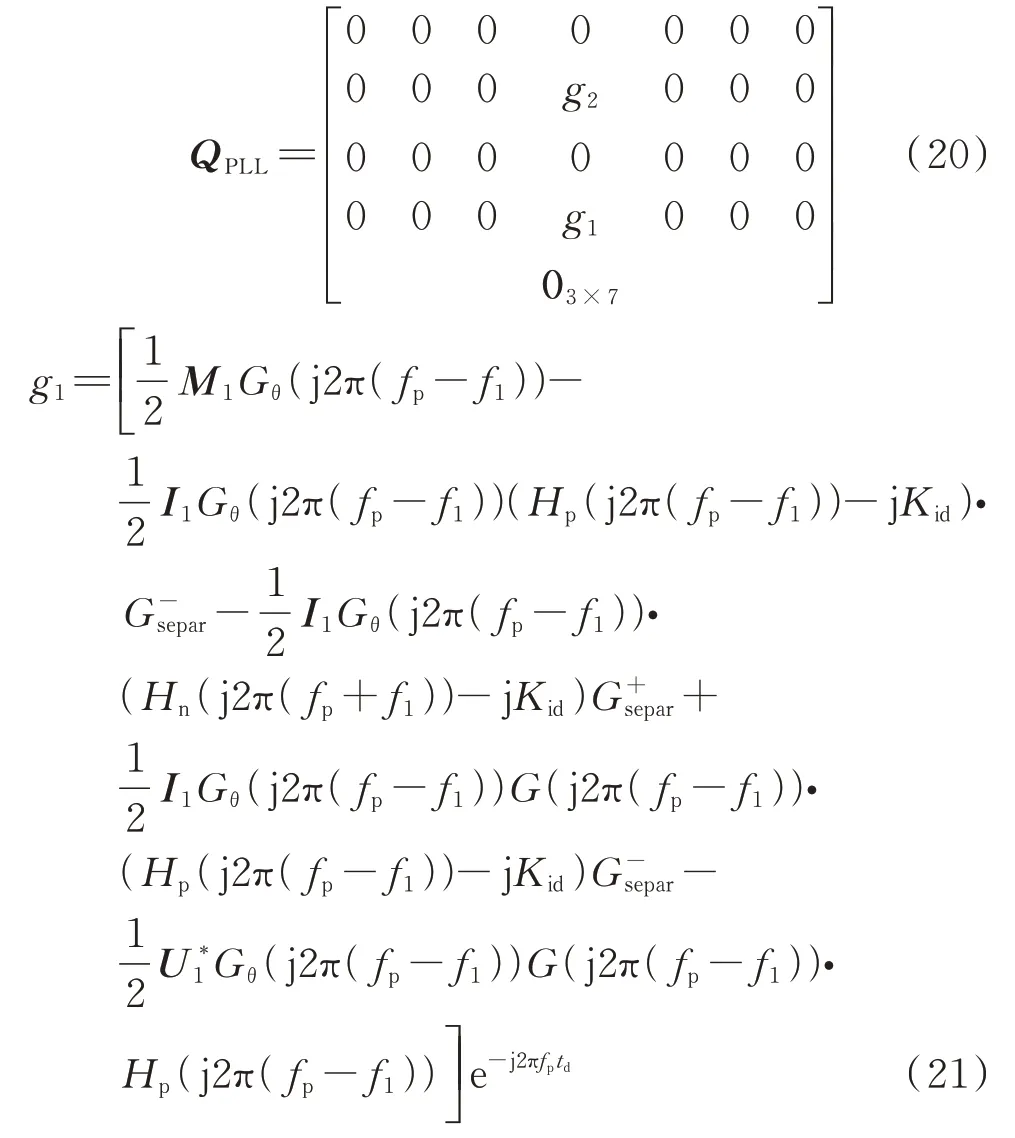
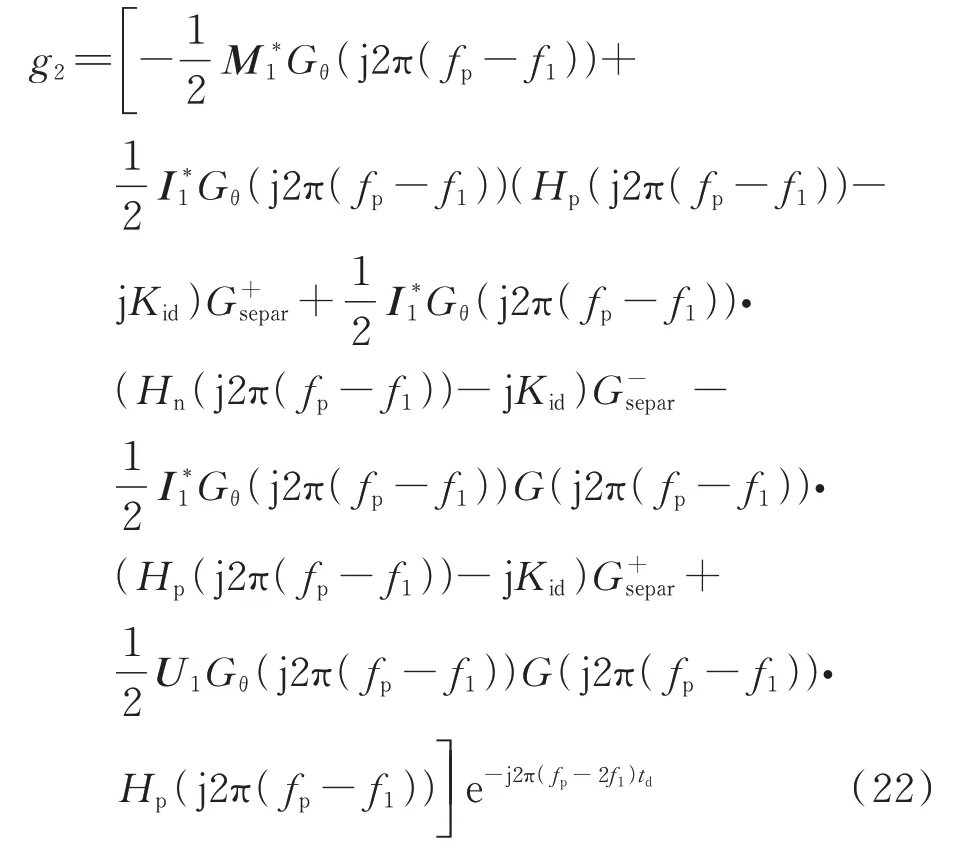
式中:M1、I1和U1分别为MMC 的调制波、桥臂电流和桥臂电容电压之和的稳态变量；*代表变量的共轭；Gθ（·）为锁相环的闭环传递函数；Kid为解耦系数。

2.3 MMC 阻抗模型的仿真验证

通过上述MMC 控制系统的小信号模型推导,可以获得式（10）中各控制环路的系数矩阵。将式（10）代入MMC 电气部分小信号模型的式（8）和式（9）中,可获得扰动电压与桥臂小信号电流的关系表达式。

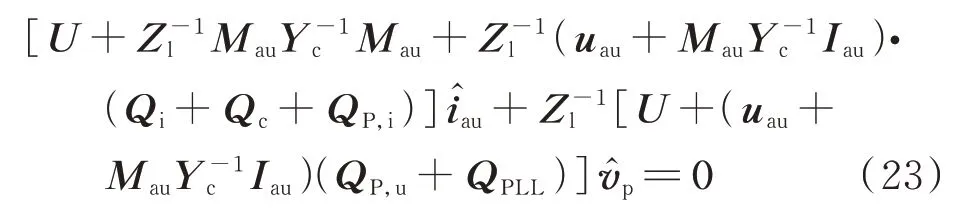
式中:U为7 阶单位矩阵。

由此,可得桥臂小信号电流与小扰动电压的7 阶导纳矩阵为:

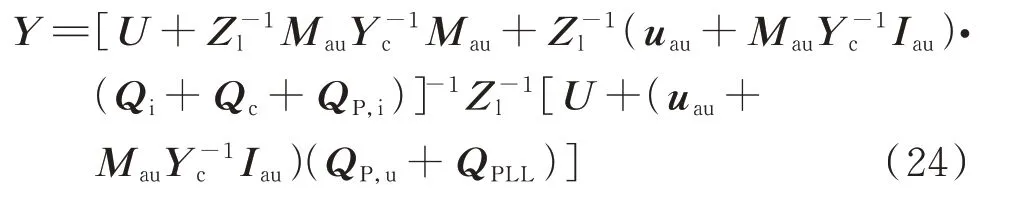
由于MMC 交流端口电流为桥臂电流的2 倍,MMC 的fp频次小信号详细阻抗模型为:

式中:Y4,4为导纳矩阵Y的第4 行、第4 列元素。

为了验证上述MMC 详细阻抗模型的正确性,在MATLAB/Simulink 平台搭建MMC 仿真模型,具体参数如附录A 表A2 所示。利用扫频法获得MMC 的阻抗,再与上述推导的阻抗模型的解析值进行对比验证。

MMC 的详细阻抗模型的解析值与仿真扫频值的对比结果如图1 所示。正负序阻抗的解析值与扫频值吻合,验证了上文所建立的考虑正负序电流控制环和序分离环节的MMC 的详细阻抗模型的正确性。

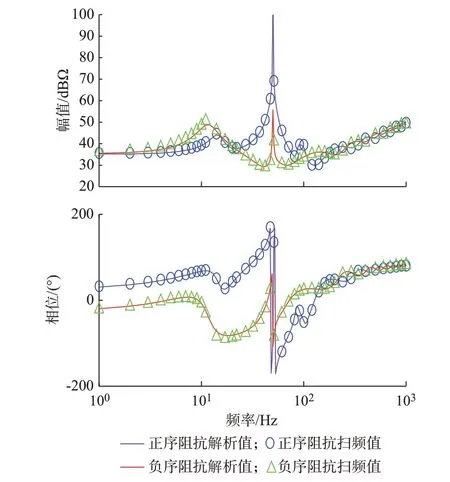
图1 MMC 阻抗扫频值与详细阻抗模型解析值对比结果Fig.1 Comparison results between frequency sweep values of MMC impedance and analytical values of detailed impedance model

3 MMC 的交流阻抗波动特性分析

3.1 序分离环节以及正负序电流控制环对MMC阻抗特性的影响

3.1.1 序分离环节对MMC 阻抗特性的影响

基于所建立的MMC 阻抗模型,分析序分离环节对阻抗特性的影响。有无序分离环节时的MMC阻抗波形对比如附录A 图A4 所示。图A4（a）中,有无序分离环节时的MMC 正序阻抗波形在低频段时趋势类似,但在中高频段差异较大。在中高频段,含有序分离环节的MMC 阻抗存在周期性波动,波动周期与基于延时对消法的序分离环节中的5 ms 延时有对应关系,虽然幅相的波动幅度随着频率的增加而衰减,但这一波动情况明显增大了MMC 阻抗的相位,使其跨越90°进入负阻尼区间,极大地降低了系统的稳定性。图A4（b）展示了有无序分离环节时的MMC 负序阻抗波形对比结果,与图A4（a）中正序阻抗的结论类似,当考虑序分离环节时阻抗出现了波动现象,而当不考虑序分离环节时阻抗则没有波动现象。

可见,有无序分离环节是阻抗波动的关键因素。为了提高系统稳定性分析的精确度,在MMC阻抗建模的过程中,有必要根据实际系统的控制结构充分考虑序分离环节。

3.1.2 正负序电流控制环对MMC 阻抗特性的影响

保持正序电流控制环比例系数kinnerP不变,仅改变负序电流控制环比例系数kinnerN,此时正负序电流环控制器参数的一致性发生改变,其对阻抗的影响展示于图2。

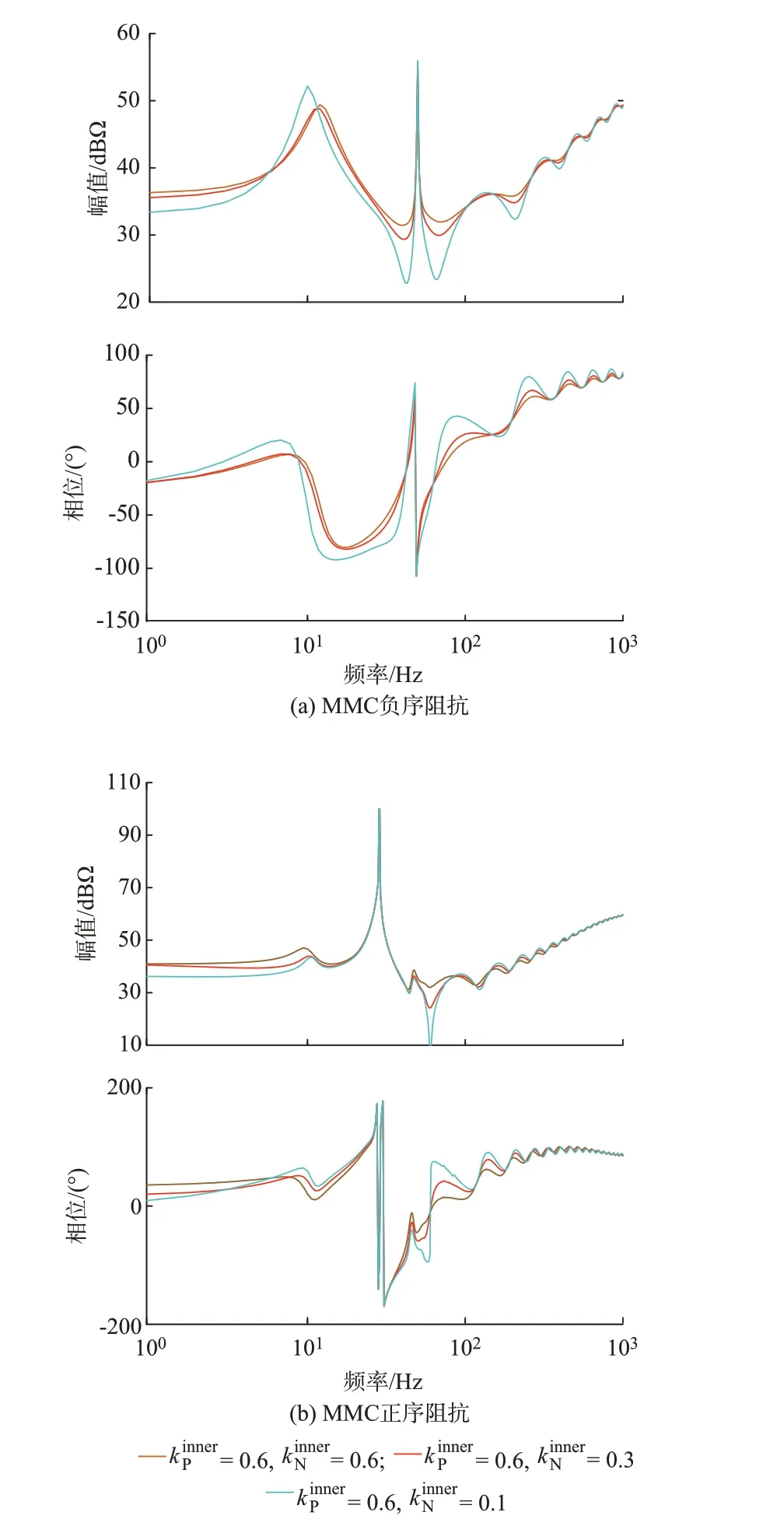
图2 正负序电流环控制器参数一致性变化时的MMC 交流阻抗Fig.2 AC impedance of MMC with changing consistency of controller parameters of positive-negative sequence current loop

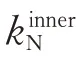
因此,需要注意的是,正负序电流环控制器参数的一致性对阻抗特性有较大影响。随着正负序电流环控制器参数不一致性的增加,阻抗的波动将进一步加剧,这会进而削弱系统的稳定性。

3.2 阻抗波动现象的机理分析

基于上文推导的MMC 详细阻抗模型,3.1 节通过改变控制系统的参数,体现当考虑正负序电流控制环和序分离环节时MMC 阻抗存在规律性波动这一特性,同时也发现了MMC 阻抗的波动性不仅与序分离环节密切相关,而且与正负序电流控制环的控制器参数的一致性有关。

虽然MMC 的详细阻抗模型可以展现精确的阻抗特性,具有数学上的严密性,有利于体现MMC 阻抗的所有细节特性,但由于MMC 的详细阻抗模型中包含所有的控制环路和3 次谐波,这势必导致MMC 的详细模型非常复杂,难以直观、简练地体现出所关心的核心阻抗特性的影响因素。因此,以往通常通过调节相关参数或控制环节来获取多组对应的阻抗波形,再通过对比所得的多组阻抗波形的差异性来分析相关参数或控制环节对阻抗的影响,这种“图形法”比较直观易懂,但不能从数学理论上阐明某些阻抗特性的机理,尤其是当多个因素共同影响某些频段阻抗特性时,“图形法”往往就显得力不从心。

鉴于此,本文在MMC 的详细阻抗模型的基础上,推导出MMC 的简化阻抗模型,并尝试利用简化阻抗模型着重关注核心要素,从理论上阐述MMC阻抗波动特性的相关机理。

为了获取MMC 的简化阻抗模型,在前文所建立的详细阻抗模型的基础上,忽略外环影响将相关控制环节的系数矩阵置零,忽略高次谐波影响及系统延时,基于式（24）和式（25）,MMC 的简化阻抗模型可以表达为:

式中:Zl为桥臂电感在fp频次下的感抗值；Yc为桥臂等 效 电 容 在fp频 次 下 的 导 纳；Mau、uau和Iau分 别 为 系统稳态时调制波、上桥臂电压之和以及上桥臂电流中的直流分量,在稳态下均为定值,所以MMC 的阻抗Z的规律性波动主要受a2影响,a2的数学特性是需要重点挖掘的关键点。可见,该简化模型除了包含MMC 系统的相关硬件参数外,还包含了电流环的控制特性。

对比以往阻抗建模的研究成果,本文的研究重点是MMC 交流阻抗的波动性这一特殊现象。因此,只有在上文推导的MMC 简化模型能够体现本文所关注的阻抗波动现象的情况下,简化模型在本文中才具有应用价值。

MMC 的简化阻抗模型和详细模型的对比结果如图3 所示。

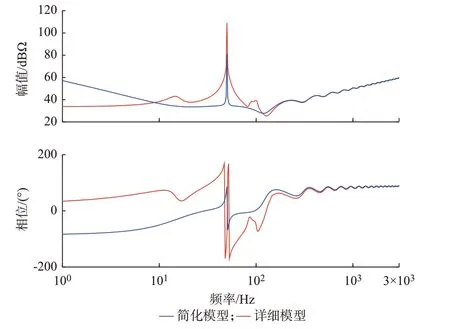
图3 MMC 阻抗的简化模型与详细模型对比Fig.3 Comparison between simplified model and detailed model of MMC impedance

由图3 所展示的MMC 详细阻抗模型和简化阻抗模型的对比结果可见,简化模型由于忽略了fp频次以外的谐波和外环等环路,其在低频段与详细模型存在较大差异,但在中高频段与详细模型基本保持一致,尤其是在阻抗波动的频段简化模型与详细模型具有较好的一致性。这充分表明,简化模型能够表征阻抗波动这一特性,用简化模型来有针对性地分析阻抗波动这一问题是合理的。

MMC 阻抗的简化模型（式（26））中的a2为电流内环系数矩阵中的fp频次元素,在式（12）中已有详细表达,在此关注核心问题。忽略系统延时及解耦环节,其表达式详细列写如下:

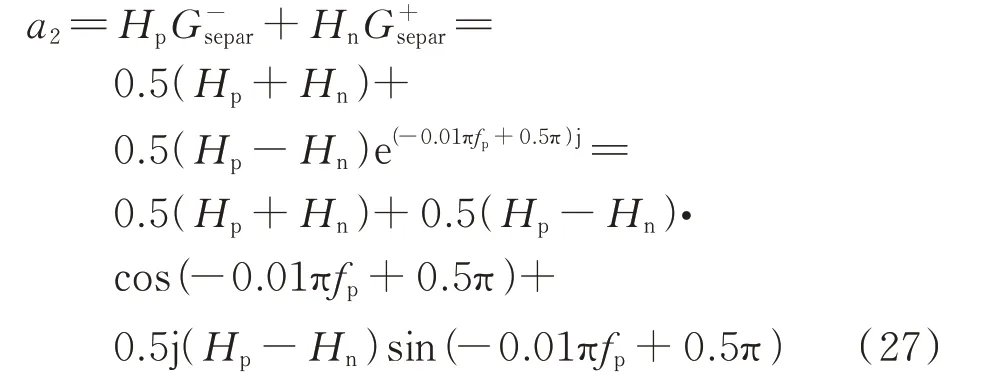
可见,a2中含有关键的正弦、余弦函数,这会导致其呈现出周期性波动现象。

以a2的模值为例分析其波动性:

式（28）中的Hp和Hn分别表示正序电流环控制器传递函数和负序电流环控制器传递函数（本文中均使用比例-积分（PI）控制器）。

由式（28）可见,当Hp和Hn为确定值时,a2的模值表达式包含余弦函数,将呈现出周期性波动的特性,a2的模值的确是随着fp频次的改变而规律性改变的。

MMC 的简化阻抗模型（式（26））中,a2是其中的关键部分。虽然,式（26）中的桥臂电感的感抗值Zl和桥臂等效电容的导纳值Yc也会随着fp频次的变化而发生改变,但由于式（26）中的各部分为叠加关系,并不会影响式（26）中的a2所体现的余弦函数的周期性波动特性,这就是MMC 阻抗幅值所体现出的周期性波动的机理。

MMC 的简化阻抗模型（式（26））中的B部分与a2是相乘关系,因而B部分对波动量a2有缩放作用,a2B共同体现出波动量的剧烈程度,B部分随着fp频次的增加而逐渐减小,最终趋于稳定值uau,这就解释了随着频率的增加MMC 阻抗的波动幅度逐步减小的原因；而式（26）中的A部分中的桥臂电感的感抗值Zl随着fp频次的增加而逐渐增大,同时桥臂等效电容的导纳值Yc则逐步减小,故在高频段,A部分主要体现的是感抗的特性,而B部分随着fp频次的增加而逐渐减小。因此,在高频段MMC 的阻抗主要是以A部分的特性为主,体现的是A部分中以MMC 桥臂电感Zl为核心的电感特性。

3.3 正负序电流环控制器参数的不一致性影响阻抗波动特性的机理分析

下文利用上述MMC 阻抗简化模型从理论上推导正负序电流环控制器参数的不一致性会增加MMC 阻抗在相应频段的波动性这一结论。

在MMC 阻抗波动的一个变化周期内,通过阻抗的波峰值与波谷值之差可以体现MMC 阻抗的波动剧烈程度。下文求解MMC 阻抗在一个波动周期内的阻抗波峰值与波谷值之差。

在3.2 节中,已经得到a2B共同体现出阻抗波动量的剧烈程度这一结论,但在中高频段B部分趋于稳定值uau,受频率变化影响较小,因而此处重点分析a2模值的波峰值与波谷值之差。在MMC 阻抗的一个波动周期内,当|a2|中的余弦函数为1 时,a2的模值|a2|取得最大值:

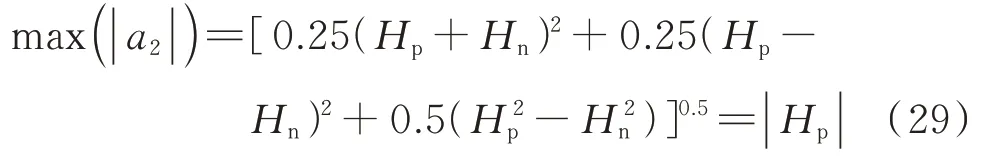
当|a2|中 的 余 弦 函 数 为-1 时,a2的 模 值|a2|取得最小值:

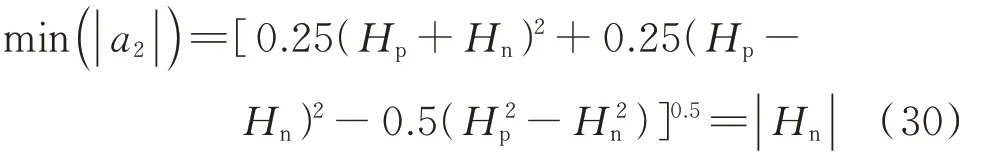
因此,a2的模值在一个变化周期内,表征波动幅度大小的表达式为:

以最常见的PI 控制器为例进行分析。正序电流环控制器传递函数Hp和负序电流环控制器传递函数Hn的控制参数差异越大,则a2的模值波动越大。进而,根据MMC 的简化阻抗模型（式（26））可知,a2的模值波动越大则MMC 的阻抗波动越大。这就是MMC 交流阻抗波动会随着正负序电流环控制器参数不一致性的增加而进一步加剧的影响机理。

4 正负序电流环控制器参数的不一致性对MMC-HVDC 系统稳定性的影响分析

MMC-HVDC 系统的整体结构框图如附录A 图A5 所示。MMC 经变压器交流并网,此处定义变压器的阻抗及交流线路阻抗统一包含在电网阻抗中。模型的具体参数与附录A 表A2 保持一致。

本文在3.3 节中详细分析了正负序电流环控制器参数不一致性的增加会加剧MMC 端口阻抗的波动,进而恶化MMC-HVDC 系统的稳定性。下文利用阻抗稳定判据,通过理论分析和实验进一步验证上述结论的正确性。

根据阻抗稳定判据［9］,MMC 并网系统的稳定性取决于MMC 阻抗与电网阻抗的幅值交点处的相位裕度。MMC 与电网的阻抗波特图如图4 所示。

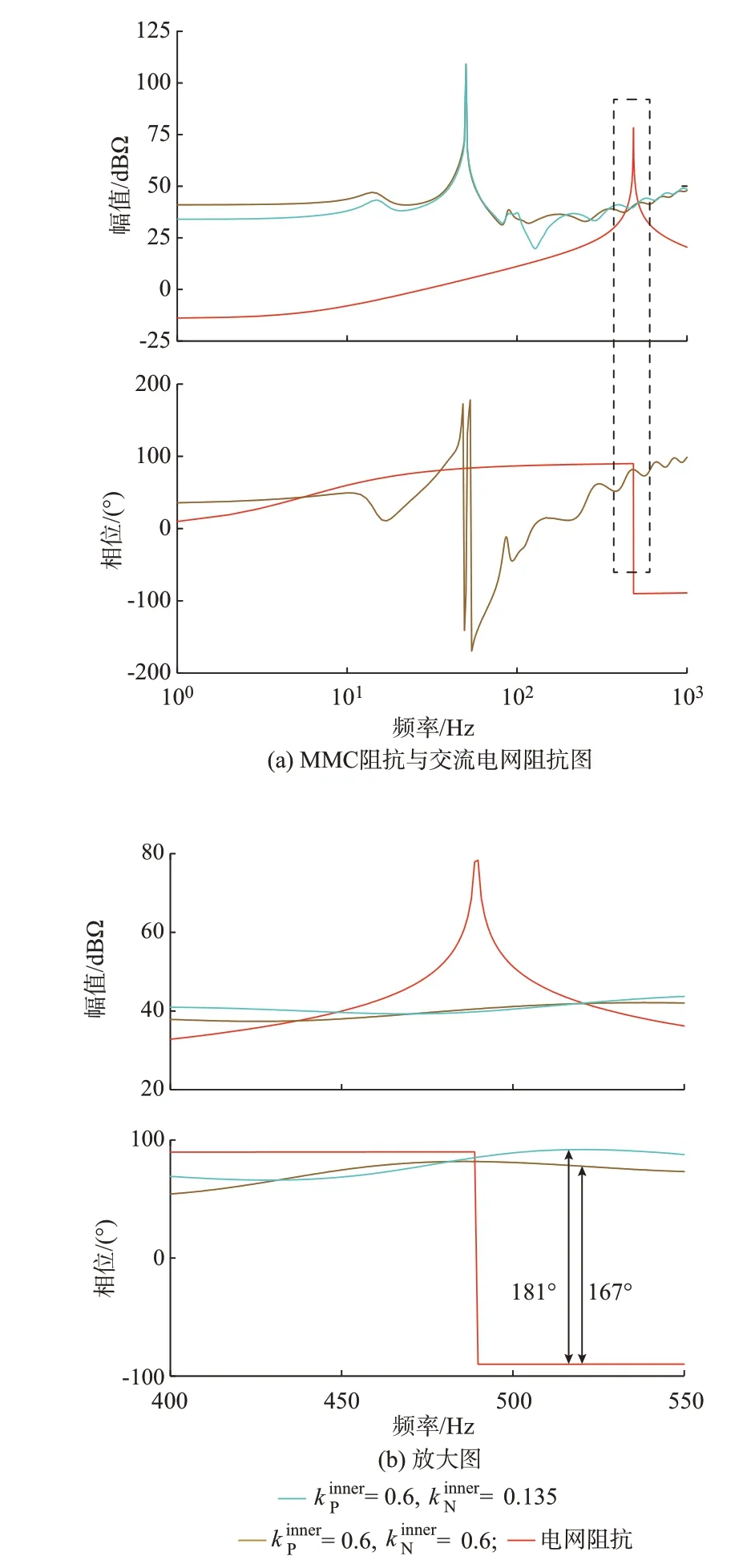
图4 正负序电流环控制器参数的不一致性对MMC 并网系统阻抗的影响Fig.4 Influence of inconsistency of controller parameters of positive-negative sequence current loop on impedance of MMC grid connected system

可见,电网阻抗与这两种情况下的MMC 阻抗的幅频曲线在517 Hz 附近均存在交点。但是,当正负序电流环控制器参数一致时,MMC 阻抗与电网阻抗幅频曲线在517 Hz 处交点相位差是167°,有足够的相位裕度；但当正负序电流环控制器参数不一致时,MMC 阻抗与电网阻抗幅频曲线在517 Hz 处交点相位差为181°,说明系统稳定裕度不足,系统不稳定。上述分析再次证明,正负序电流环控制器参数的不一致性会加剧由正负序分离带来的MMC 阻抗波动现象,从而进一步降低系统的稳定性,甚至存在引发系统失稳的风险。

为了验证上述关于MMC-HVDC 系统稳定性理论分析的正确性,本文利用硬件在环平台进行实验验证［28］,实验平台如附录A 图A6 所示,模型的具体参数与附录A 表A2 保持一致。

实验验证了柔直输电系统正负序电流环控制器参数变化前后的系统状态变化,公共耦合点（PCC）处a 相电压和电流变化的实验录波如附录A 图A7所示。当正负序电流环控制器参数由一致切换到不一致时,发现PCC 处a 相电压和电流逐步发生振荡,电压和电流中出现了高频谐波。

对系统失稳后的PCC 处电压和电流进行快速傅里叶变换（FFT）分析,PCC 处电流的总谐波畸变率（THD）为54.41%。可见,其谐波含量非常高,远远超出了系统稳定运行的额定要求。同时,其谐波的频率主要集中在517 Hz 附近,这与图4 中基于阻抗法的分析结果保持一致,证明了上述基于阻抗法的MMC-HVDC 系统稳定性分析结果的正确性。可见,正负序分离带来了MMC 阻抗的波动,降低了系统的稳定性,而正负序电流环控制器参数的不一致性会进一步降低系统的稳定性,验证了上述理论分析结果的正确性。

5 结语

在MMC 采用基于延时对消法的序分离算法和正负序电流控制环的情况下,本文基于MMC 的详细阻抗模型,深入研究了柔直系统交流阻抗波动这一特殊现象。基于MMC 的简化阻抗模型,从理论层面阐述了交流阻抗波动现象的产生机理。同时,针对正负序电流环控制器参数的不一致性会加剧阻抗波动这一现象,开展了相应的数学推导,从理论上进行了机理分析。

综上所述,针对实际工程的柔直系统,在MMC阻抗建模过程中,有必要将其所采用的序分离算法和正负序电流控制环都考虑在内,从而得到更符合实际工程且能体现出某些特殊阻抗特性的阻抗模型。当序分离环节采用基于延时对消法的序分离算法时,会导致交流阻抗存在波动现象,而且正负序电流环控制器参数的不一致性会加剧阻抗波动,这些现象均会削弱柔直系统的稳定性。上述现象是柔直系统振荡的关键因素之一,在柔直系统稳定性分析中不能忽略甚至应被重点关注。

本文所研究的考虑正负序电流控制环和序分离算法的MMC 阻抗建模以及相关稳定性问题,是在对称三相系统前提下进行的研究,本文的研究成果是不对称系统以及其他更加复杂电网系统下的相关问题的研究基础。针对更加复杂的不对称系统、含有背景谐波的电网系统下的相关问题,仍有待进一步研究。