适应新型电力系统的高性能电磁暂态仿真技术及其应用

熊 卿，张路寅，张庆华，张东院，范圣韬，王 良

（1. 积成电子股份有限公司,山东省济南市 250100；2. Quark Power Inc.,萨里V3Z6P4, 加拿大）

0 引言

国家电网有限公司的“十三五”“十四五”规划明确提出,要进行大规模交直流电网电磁暂态仿真技术研究和平台建设,提升全电磁暂态仿真能力,实现对于电网特性的精准认知。基于瞬时波形表示的电磁暂态仿真技术成为公认的支撑技术之一［1-4］。

电磁暂态仿真技术早期侧重于输电线路过电压计算,逐步扩展到包含同步发电机动态特性的机电暂态过程研究［5-7］,发展至今已在交直流混联输电及大规模新能源接入等方面获得成功应用。在以新能源为主导的新型电力系统背景下,复杂大电网的全电磁暂态仿真已成为研究和应用的热点之一。

然而,由于电磁暂态仿真基于时域波形精确描述电磁暂态过程,其数学模型精细复杂、计算步长小、计算开销大,导致仿真速度较慢、模型规模较小,难以适应以大规模电网、高比例新能源和密集电力电子变换器为结构特点的新型电力系统［8-16］。因此,需要在提高万节点级大规模交流电网全电磁仿真效率的同时,兼顾深度电力电子化电网内不同时间尺度系统的计算精度。面临的主要挑战如下。

1）适应新型电力系统全电磁仿真的准确元件模型

新型电力系统包含复杂的交直流输电系统和密集的电力电子变换器,其各类基础元件模型不仅要求达到与当前主流电磁暂态技术相当或更好的精度水平,而且要能够以统一的模式适应传统小步长电磁暂态和新一代大步长电磁暂态算法［17-18］,以实现在较宽时间尺度范围内稳定精确的仿真计算。

2）大规模乃至超大规模交流电网的全电磁暂态仿真效率

新型电力系统构建于广泛互联的交流大电网网架基础,因而需要利用电磁暂态算法理论的新成果,并充分挖掘电磁暂态程序底层实现的潜力,力图在集约化通用硬件上大幅度提升交流电网全电磁暂态仿真的效率,达到数万节点级超大规模交流系统的实用化全电磁暂态仿真能力。

3）大电网背景下不同计算步长电力电子系统的混合速率仿真

新型电力系统具有以新能源为主体、多电力电子变换器密集接入的特征,电力电子设备与互联电网紧密耦合。需要实现交流大电网和不同计算步长电力电子小系统的多速率混合仿真,从而兼顾整体计算效率和不同时间尺度系统的仿真精度。

4）简化大规模复杂电网的全电磁暂态建模仿真和数据分析过程

新型电力系统全电磁暂态仿真面临着高效建模和有效分析等操作层面的问题。一方面,要能根据边界条件灵活方便地构建电磁暂态全网模型,快速平稳地启动并进入有效仿真时段；另一方面,需要全面观测大电网模型仿真的状态,以便批量化开展仿真数据的有效甑别和分析。

由积成电子股份有限公司自主开发的新一代高性能电磁暂态仿真平台（GTS）突破了关键电磁暂态模型的技术瓶颈,实现了具备良好计算精度和稳定性的基础模型；基于最新的IT 技术架构和高性能底层网络求解器,实现了时域变换大步长电磁暂态算法［17］和矩阵分网并行技术［19］,全面提升了大规模乃至超大规模电网的电磁暂态仿真效率；结合精确稳定的仿真接口,实现了复杂大电网空间多速率全电磁暂态仿真。

本文从研发角度,简要介绍新一代高性能电磁暂态仿真平台的研发思路、关键技术以及所达到的效果。

1 高精度电磁暂态模型

无论是实现诸如过电压计算、电力电子设备仿真等传统应用,还是解决新型电力系统仿真面临的算法稳定性和计算效率问题,电磁暂态仿真都建立在精确电力元件模型的基础之上。本文以有代表性的3 种关键难点模型（同步发电机模型、传输线模型和电力电子器件模型）为例说明已具备的精度水平。

1）同步发电机模型

同步发电机是电磁暂态仿真领域的重难点模型之一,尤其对于包含大量同步发电机的大规模新型电网,其精度水平直接影响到系统级仿真的准确性和稳定性。更重要的是,在实现大步长电磁暂态仿真算法时,对发电机模型精度的一致性和较大步长时的数值稳定性又提出了更高的要求。

传统基于接口型的发电机模型已不能很好地适应上述大电网系统级仿真的要求。由于发电机和网络部分采用独立交替求解的方式,接口部分的电气量存在一个步长时延,严重降低了发电机模型的数值稳定性,更无法适应毫秒级的大步长电磁暂态仿真［20-24］。

新一代高性能电磁暂态仿真平台采用电机-网络联立求解方法,显著提高了电机模型在宽时间尺度范围内的数值稳定性和仿真精度。附录A 中介绍了同步发电机模型的特性,并开展了详细的测试对比。结果表明,所开发模型在微秒至毫秒级范围内均能准确一致地仿真发电机的动态响应,具备较高的仿真精度,并在微秒级至毫秒级宽步长范围内保持良好的数值稳定性。

2）传输线模型

传输线模型作为电磁暂态仿真领域的核心模型,已成为反映电磁暂态产品技术水平的重要标志之一,也是自主化道路上难度较大的技术壁垒。对传输线特性的准确仿真需要精确地模拟传输线的分布参数效应以及由趋肤效应、大地返回阻抗等因素造成的参数频率相关特性［25-31］。

在新型电力系统的仿真应用中,准确的传输线模型的重要性则更为突出。一方面,对于广泛接入的各种直流输电系统以及分布式新能源场站,必须准确模拟内部各类线缆的宽频范围特性,才能正确仿真其动态响应和控保动作过程；另一方面,对于所面临的各类谐波及振荡问题,需要在强耦合系统内使用频率相关传输线模型,才能开展准确分析。

在新一代高性能电磁暂态仿真平台开发过程中,一直将自主化实现传输线模型作为研究重点,目前已开发了多种类型传输线模型。附录B 对新一代高性能电磁暂态仿真平台的传输线模型做了简要介绍,以架空线和管状地下电缆的频率相关模型为例分别进行了开路和短路测试［32-34］,并与频域仿真结果［32-36］和业界主流的电磁暂态工具的仿真结果进行了对比。结果表明,所开发的传输线模型具备良好的精度和数值稳定性。新一代高性能电磁暂态仿真平台也成为少数具有完备传输线模型的仿真工具之一。

3）电力电子器件模型

电力电子器件及控制系统建模仿真能力的发展,推动了电磁暂态仿真技术在直流输电系统和交直流相互影响等方面的成功应用,也成为当前新型电力系统仿真应用的重要基础。

电力电子器件的仿真关键在于如何精确高效地处理开关动作过程和抑制数值振荡等问题［37-39］。附录C 中介绍了新一代高性能电磁暂态仿真平台电力电子模型的技术特点,并以10 电平模块化多电平换流器（MMC）模型为例说明了所开发电力电子元件模型的仿真精度和效率。

2 大规模交流电网的高效全电磁暂态仿真技术

传统电磁暂态程序主要关注设备级小系统瞬态过程的仿真,对模型规模和计算效率要求不高。在新型电力系统背景下,则难以满足广泛互联大电网全电磁暂态仿真的性能需求。

随着高性能信息通信（IT）技术的发展和电磁暂态算法理论的突破,电磁暂态仿真技术已具备更先进的实现基础和巨大的提升空间。在新一代高性能电磁暂态仿真平台开发过程中,以仿真效率为优先目标,充分利用已有的技术和理论成果,突破了电磁暂态技术在规模和效率方面的瓶颈。为简化起见,以高效自动分网并行技术和时域大步长电磁暂态算法理论为例,简要说明其理论基础和实现效果。

2.1 电磁暂态自动并行仿真技术

利用现代计算机多核心多线程计算能力,对大电网进行分网并行仿真,是提高大规模电网全电磁暂态仿真效率的最为直接有效的方式之一。传统电磁暂态程序常利用分布式传输线的传播延时进行分网,需要手动划分子网区域,不但增加了使用上的困难,而且不易实现良好的计算负载平衡。

新一代高性能电磁暂态仿真平台利用了基于矩阵分网的并行技术［19,40-42］,实现不依赖于传输线传播延时的全自动分网和并行计算。仅须指定需要并行的线程数量,底层算法自动根据硬件资源情况实现多线程负载均衡的并行计算,更充分地发挥了现代计算机多核心计算资源优势,并提高了电磁暂态并行仿真的易用性。

典型的电磁暂态计算负荷可分为两部分,一是节点导纳方程的求解,二是各元件伴随电路的生成及状态更新,对于这两部分计算负荷可以分别采用不同的并行策略［19,25,37］。

对于节点导纳方程式（1）的求解,可以通过基于图的算法将系数矩阵Y变为如式（2）所示的对角加边形式。

式中:J为已知的右端电流向量；v为待求的节点电压；Yij为子块矩阵。

利用对角子块矩阵Yii(i=1,2,…,m）的独立性,在节点导纳方程求解过程中可以方便地实现LU 分解、前代和回代过程的并行计算［19,42］。

对于伴随网络的生成和状态更新部分,由于其计算所需要的量已知,计算本身不存在相互依赖性,因而可以方便地实现高效率的并行。将系统中所有同类型的元件（如变压器、发电机等）分为一组,再将这一组内每个元件的计算平均分配给各计算线程,可以达到优良的计算负载平衡［19］。

如图1 所示,对于一个万节点级实际电网,新一代高性能电磁暂态仿真平台可实现良好的并行效果。加速比α=t1/t2,其中t1为单线程计算耗时,t2为多线程计算耗时。

图1 中测试电网包含12 000 多个三相节点、7 000 多条支路和9 000 多台变压器,约1 700 台同步发电机；采用50 μs 计算步长仿真10 s,分别使用π线路模型和Bergeron 线路模型。单线程时π 线路模型耗时2 134 s（约36 min）、Bergeron 线路模型耗时2 256 s（约38 min）,在使用32 个线程仿真时计算耗时大约为2 min。

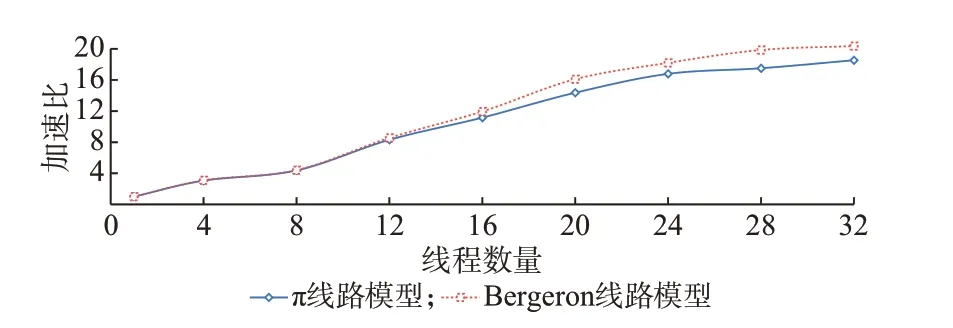
图1 多线程并行加速比统计曲线Fig.1 Statistical curves of multi-thread parallel speed-up ratio

可见,新一代高性能电磁暂态仿真平台的加速效果随着并行线程数量的增加呈现近似线性的增长趋势,表明所实现的并行仿真达到了较高的性能水平。

2.2 大步长电磁暂态仿真技术

基于时域变换的大步长仿真算法［17-18］,是利用电网中电气量的正弦波主导特征,通过将电气量变换为缓变信号,在保证计算精度的前提下增大电磁暂态仿真的计算步长［17,43-45］。

基本思路是首先为原系统的量x(t)构造一个近似正交的量y(t),然后通过一个如式（3）所示的旋转变换将正弦基波主导的信号变换为变化更为缓慢的信号u(t)和v(t)。

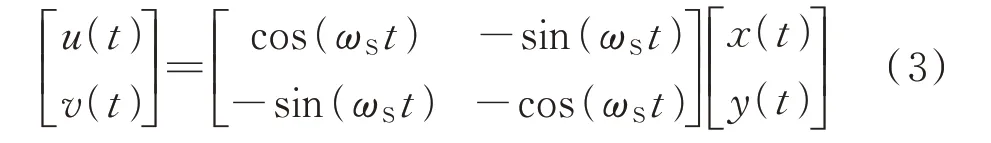
式中:ωS为新引入的仿真参数,常设置为交流系统基频。

当使用某种数值算法（如梯形法）在u-v坐标系下离散化后,进一步通过式（3）的变换关系可得到原始x-y坐标系下的新离散公式（式（4））。

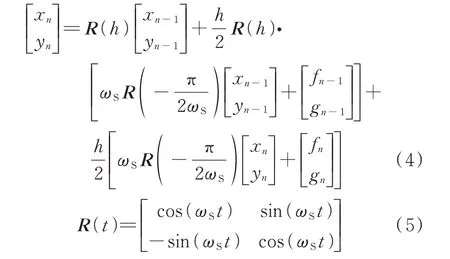
式中:h为离散化的步长；R为新引入的一个矩阵；f和g为变量x(t)和y(t)所满足的微分方程,如式（6）所示。

式（4）实质上是在缓变的u-v坐标系下进行离散化,因此可在保证良好数值精度的前提下增大计算步长,从而有效提高电磁暂态仿真的计算效率。

通过大步长电磁暂态与小步长电磁暂态仿真算法的有机融合,新一代高性能电磁暂态仿真平台统一了不同步长计算引擎的模型及参数,隐藏了不同引擎实现及应用的复杂性,实现了精确稳定的工业级大、小步长电磁暂态计算引擎和宽时间尺度（微秒级到毫秒级）的全电磁暂态高效稳定仿真。

为了进一步提升大规模交流系统的仿真速度,可以将并行仿真技术和大步长仿真方法结合起来,实现支持并行仿真的大步长电磁暂态仿真。传统的基于传输线分网的并行技术在应用于大步长电磁暂态仿真时,由于计算步长常常大于分布式传输线的传播延时,因此会受到诸多的应用限制；而2.1 节所介绍的基于矩阵分网的并行仿真技术,由于其实现不依赖传输线传播延时,非常适合于大步长电磁暂态的并行仿真。

通过将自动并行仿真与时域变换大步长仿真技术相结合,可以实现数千节点级大电网的超实时电磁暂态仿真。如某省级电网220 kV 以上主网架包含约3 200 个三相节点、约3 500 条支路和约120 台带调节系统的同步发电机,仿真30 s 时长。采用不同计算步长和并行线程数量时的仿真耗时统计如表1 所示。其中,h为仿真步长。

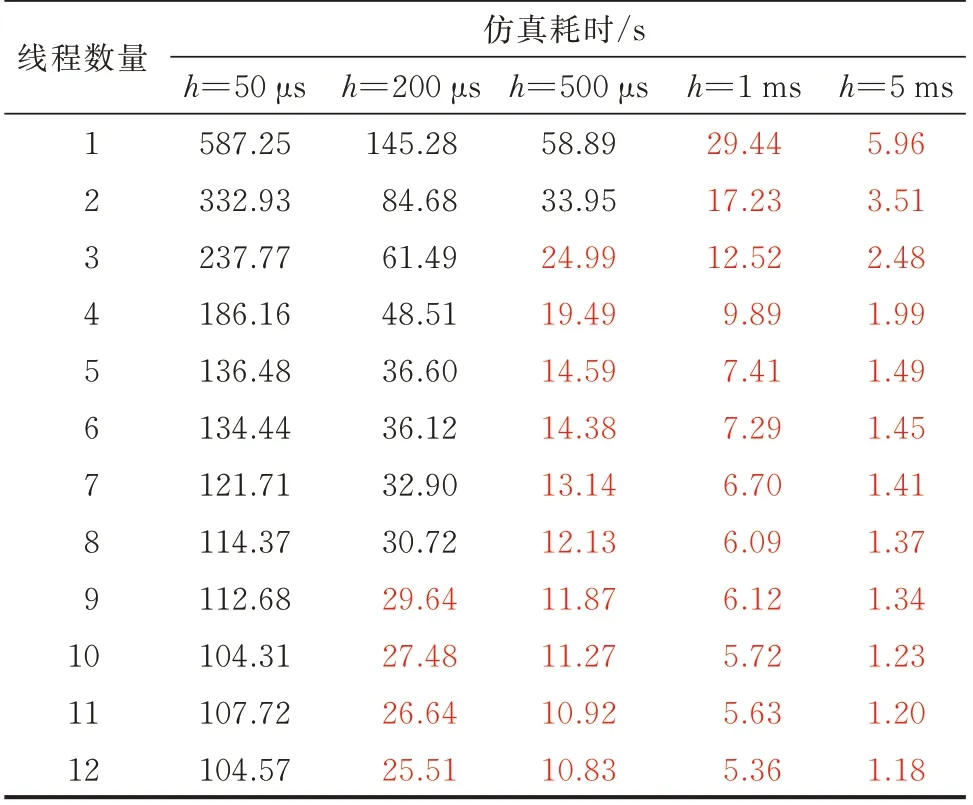
表1 不同计算步长和并行线程数量的仿真耗时统计Table 1 CPU time of simulations with different calculation steps and numbers of parallel thread

表中,红色数字表示实现了超实时仿真,最快可在1.18 s 内完成全网30 s 的电磁暂态仿真计算。该省级电网模型所采用的发电机及其调节系统仿真结果示例详见附录D。

3 多时间尺度复杂电网的混合速率仿真方法

新型电力系统具有深度电力电子化的特性,使得其全电磁暂态仿真面临着强耦合多时间尺度系统的准确仿真问题。

结合第2 章介绍的统一大、小步长的电磁暂态仿真技术,通过开发高性能多速率接口将复杂大电网划分为多个子网区域,各子网可分别采用不同的计算步长,进而实现全系统的电磁暂态空间多速率仿真,很好地解决上述多时间尺度系统的仿真问题。

3.1 复杂大电网混合速率仿真

图2 展示了复杂大电网多速率混合仿真的应用方式。图中通过传输线将大电网划分为若干子区域,各区域分别采用不同的计算步长（1 μs～1 ms）,各区域之间采用多速率或等速率的传输线接口连接。

图2 大电网全电磁暂态多速率仿真示意图Fig.2 Schematic diagram of multi-rate full electromagnetic transient simulation for large-scale power grid

由于不同步长区域都是采用电磁暂态仿真,因而各区域间的接口物理意义清晰、实现简单、接口精确度高且数值稳定性好。

通过混合多速率的全电磁暂态仿真方式,不需要全网按照暂态过程最快的子系统或区域使用很小的计算步长,可以为不同时间尺度的子系统独立选择合适的计算步长；同时,在包含大量电力电子设备的大规模新型电力系统中,为避免因电力电子设备动作事件在全网传播影响仿真效率,采用分布式传输线的等速率/多速率接口实现事件传播的有效隔离,使得插值和数值振荡抑制等操作仅作用于引起事件的局部系统；可以在保证计算精度的前提下大大提高多时间尺度大系统的整体仿真效率,满足在大电网背景下灵活有效地开展强耦合电力电子化系统的交互影响研究的需求。

3.2 多速率仿真接口设计

大电网的混合速率仿真依赖于连接不同仿真步长子系统的多速率接口,基于经典电磁暂态仿真算法的多速率接口已经有不少文献进行了深入的讨论［46-48］,在此不再赘述；而连接大步长电磁暂态仿真和传统小步长电磁暂态仿真的多速率接口则更有挑战性,本节主要讨论这类接口。

基于时域变换的大步长电磁仿真算法虽然在变换域u-v坐标系下离散化,但其实现却是在原始的x-y坐标系中,这为连接大步长电磁暂态仿真和传统小步长电磁暂态仿真提供了便利。类似于经典的电磁暂态仿真算法,基于时域变换的大步长电磁仿真在每个时步求解一个由电阻和电流源组成的线性网络,只是其所使用的计算步长较大；由于是线性电阻网络,因此其可以在接口母线处使用诺顿等值表示其在一个时步内的特性,不失一般性,在此假定诺顿等值为单端口网络。

基于时域变换的大步长仿真（大步长侧）与经典电磁暂态小步长仿真（小步长侧）的多速率接口如图3 所示。其中,H和h分别为大步长侧和小步长侧所使用的步长,并假设H=Nh。小步长侧包含原始子系统以及由原系统构建的近似正交子系统,小步长侧采用的是经典电磁暂态仿真常用的梯形法进行离散化。不同于大步长侧,原始子系统和正交子系统在离散化后并不会产生耦合。为了能够在每一个小步长求解,需要给出大步长侧诺顿等值在每个小步长的等值电流ix和iy,这可以通过在u-v坐标系进行插值并变换到x-y坐标系得到。假定采用线性插值,则第n个小步长的等值电流由式（7）给出:

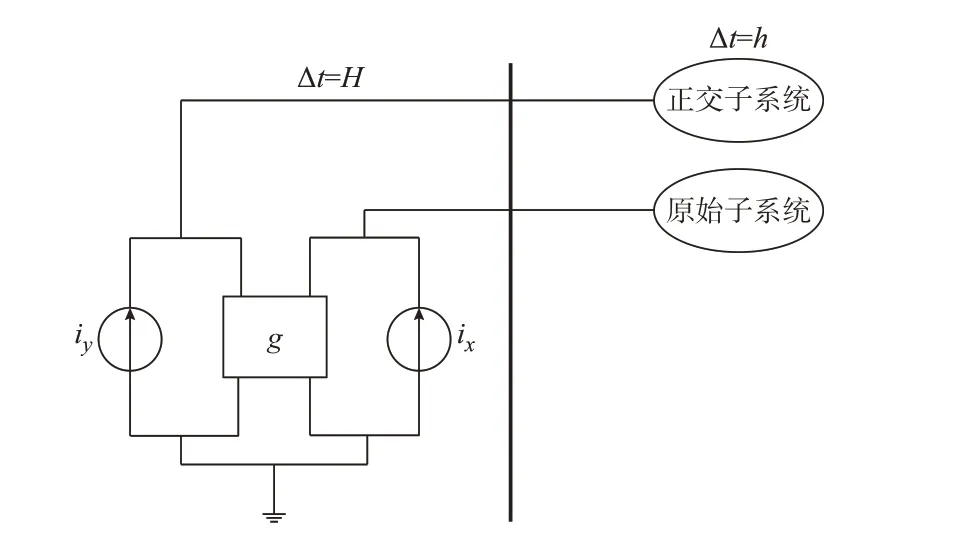
图3 多速率仿真接口Fig.3 Multi-rate simulation interface

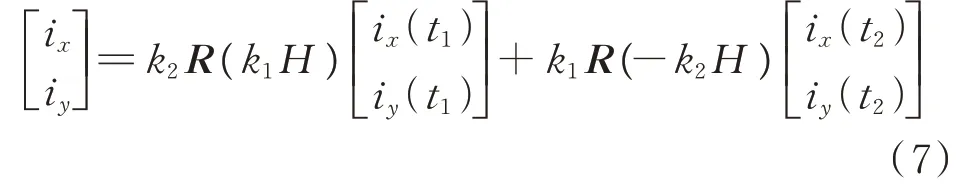
式 中:k1=n/N,k2=(N-n)/N,n=1,2,…,N；[ix(t1)iy(t1)]T和[ix(t2)iy(t2)]T分 别 为 上 一 个 大时步和当前时步计算的诺顿等值电流。

另一方面,小步长侧在最后一个小时步传给大步长侧的诺顿等值电流可以通过平滑方法防止高频分量可能造成的频率混叠现象,例如可以采用Savitzky-Golay 滤波［48］。

4 适应新型电力系统全电磁暂态仿真的实用化技术

新型电力系统的全电磁暂态仿真,不仅仅是规模和效率层面的“量变”,更是在实际应用层面引起“质变”,主要面临两方面的挑战:一是大电网全电磁暂态模型的快速灵活构建和准确初始化；二是仿真过程中全网状态的输出和观测。

4.1 电磁暂态模型的自动转换和初始化

新型电力系统的拓扑结构复杂、运行方式多变。实际应用中常希望能根据不同的系统运行方式,构建多个对应的全电磁暂态仿真模型,以便开展全面的仿真计算。

针对上述需求,新一代高性能电磁暂态仿真平台实现了基于大电网机电暂态数据的电磁暂态模型自动转换和高精度初始化。支持BPA、PSASP、PSSE 等机电数据格式,即使是万节点级规模的大规模电网,其转换过程也仅需数秒。以某省级电网为例,对比转换后电磁暂态模型的初始状态,如表2和表3 所示。

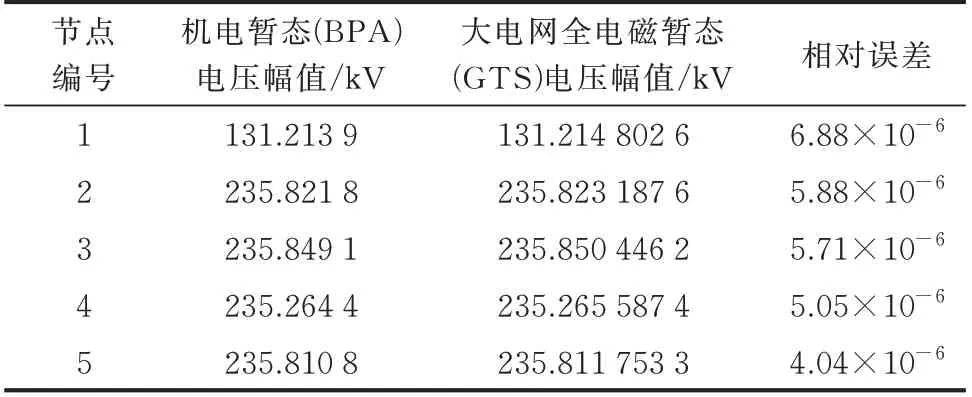
表2 全电磁暂态自动建模的节点电压精度对比Table 2 Comparison of bus voltage accuracy for full electromagnetic transient automatic modeling

表2 和表3 中对比所采用的大电网模型包含约3 200 个三相节点、约3 500 条支路和约120 台同步发电机。可见,自动构建的全电磁暂态模型初始化准确,旋转电机释放平稳,能够与初始潮流保持高度一致。

表3 全电磁暂态自动建模的节点相位精度对比Table 3 Comparison of bus phase accuracy for full electromagnetic transient automatic modeling

4.2 电磁暂态仿真的全量测输出及分析

由于新型电力系统的强控制和强耦合特性,在进行系统级仿真分析时,最好能够观测全系统的运行状态,才能明确扰动对全网运行稳定性和安全性的影响。这就要求大电网仿真时进行全量测输出,同时具备海量波形数据的查阅和处理能力。在此基础上,才可能进一步实现新型电力系统的态势感知等高级应用。

对此,研发新一代高性能电磁暂态仿真平台时充分利用底层实现的效率和大步长电磁暂态算法的特性,做到了大电网全电磁暂态仿真过程的全量测输出,即能够自动配置并输出每个交流节点的电压幅值和相位等信息。同时,还开发了海量数据的快速浏览和分析工具,可以实现几十万条密集数据波形的快速查阅和波形分析。

在第5 章超大规模交流电网的算例验证中,即对每个节点的电压都实现了全量测输出,量测规模达到模型节点规模的2 倍。

5 算例验证

为了测试新一代高性能电磁暂态仿真平台的仿真规模和效率,采用美国得克萨斯农工大学（TAMU）发布的虚拟超大规模交流电网算例［49-50］进行测试,选取了10 000、25 000 和70 000 节点系统数据（PSSE 格式）。自动转换为电磁暂态模型,系统中电源采用第1 章所述的同步发电机模型,线路采用Bergeron 线路模型,在每个三相节点均配置电压幅值和相位测量元件,实现大电网母线电压全量测输出。3 个算例中主要元件的数量统计如表4 所示。

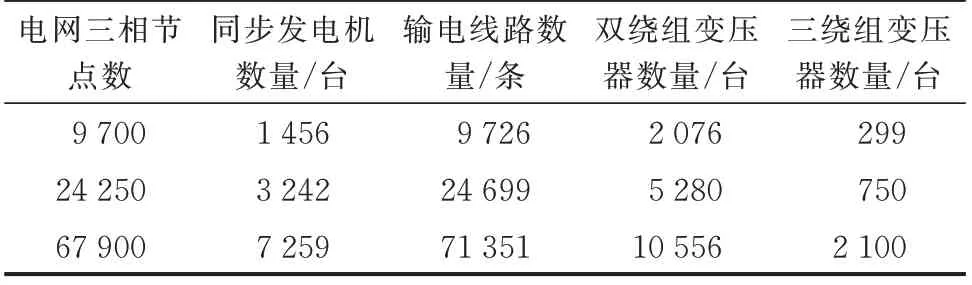
表4 大规模电网算例中主要元件数量统计Table 4 Statistics of major elements in large-scale power grid case

所有测试算例均采用50 μs 计算步长,仿真10 s。统计仿真耗时如表5 所示。其中,M为电网三相节点数。

表5 超大规模电网仿真耗时Table 5 Simulation time of super-large-scale power grid

不同线程的仿真耗时与电网规模（三相节点数）之间的关系如图4 所示。可见,随着电网规模的增大,仿真耗时基本保持线性增长,显示出新一代高性能电磁暂态仿真平台具有良好的可扩展性。

图4 超大规模交流电网仿真耗时-规模曲线Fig.4 Simulation time and scale curves of super large-scale AC power grid

对于规模最大的70 000 节点算例,采用50 μs 的步长最快仅需约15 min 即可完成10 s 的仿真。类似于2.2 节中的算例,当结合大步长仿真算法并采用更大的计算步长时,可以进一步显著地缩短计算耗时。从工程实用的角度看,对于实际电网的仿真经常还要考虑大量的电动机负荷和非线性负荷等动态元件（如:ZIP 模型中的恒功率负荷）,这可能导致仿真耗时的显著增加。附录E 以一个实际区域电网为例,详细评估了采用不同复杂度的模型对新一代高性能电磁暂态仿真平台仿真耗时的影响。结果表明,随着模型复杂度的增加,仿真耗时有所增大,但仍能够保持较高的计算效率。

利用新一代高性能电磁暂态仿真平台的大电网仿真能力,结合实际电网故障录波数据,还开展了大量的仿真对比校核工作。限于篇幅仅选取部分对比结果。

图5 所示为某省级10 kV 以上电网的故障仿真与现场故障录波对比,该电网包含约700 台发电机、9 500 个三相节点和约5 000 条线路。在220 kV 线路40.65% 处发生C 相接地故障。可见,整体上仿真波形能较好地吻合实际录波。在故障过程中,非故障相电压最大瞬时值差异约为7%（A 相）,电流最大瞬时值差异约为12%（C 相）,电流相位最大偏差约54°（A 相）。由于缺乏相关数据,目前故障点附近的输电线路仍采用较为基础的Bergeron 模型,在获得更完善的数据并采用更准确的频率相关线路模型后,预期可以获得与实测波形更为一致的仿真结果。

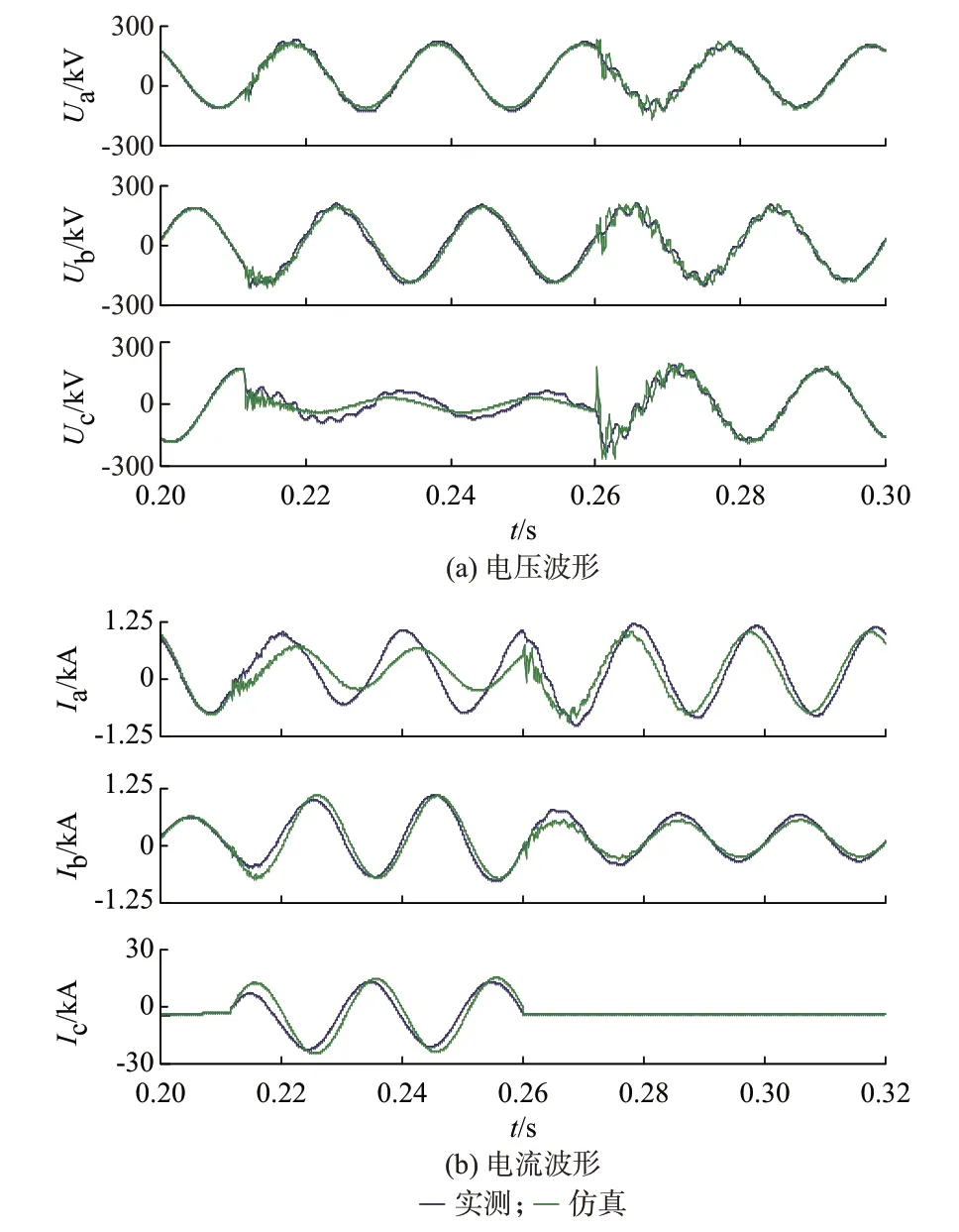
图5 某省级电网220 kV 线路C 相接地故障波形Fig.5 Waveforms of C-phase grounding fault on 220 kV transmission lines in a provincial power grid

附录F 图F1 所示为某交直流混联区域电网的换流母线近区两相短路故障录波波形与仿真结果对比。采用了跨平台联合仿真:交流大电网使用新一代高性能电磁暂态仿真平台,包含约1 700 台发电机、12 000 多个三相节点、7 000 条线路和9 000 台变压器；直流系统则采用了PSCAD/EMTDC［51］中建立的实际工程模型。通过波形对比可见,在故障暂态及故障恢复过程中仿真波形和实际录波的基本态势较为一致。

通过上述对比结果验证了采用新一代高性能电磁暂态仿真平台对大电网全电磁暂态进行仿真的准确性和实用性。

6 结语

对新型电力系统实现有效的全电磁暂态仿真,必须提高大规模交流电网的仿真效率,同时保证不同时间尺度电力电子小系统的计算精度。新一代高性能电磁暂态仿真平台通过核心模型的技术突破、时域变换大步长算法和底层自动并行技术的有效实现、空间多速率混合仿真方法的灵活应用,从多方面综合提升了电磁暂态仿真技术的性能,较好地解决了上述问题。本文简要介绍了具体的技术思路和实现效果。

在模型基础方面,解决了机网联立求解同步电机模型的仿真精度和稳定性问题,突破了包含地下电缆模型在内的各类频率相关传输线的技术瓶颈,实现了电力电子模型的高效精确仿真。在大规模交流电网仿真能力方面,实现了工业级应用的高效自动分网并行技术和基于时域变换的大步长电磁暂态算法,将省级主网架电磁暂态仿真效率提升至超实时水平,实测的最大仿真规模已达约70 000 个三相节点。在多时间尺度系统仿真精度方面,以精确稳定的多速率接口实现电力电子化大系统的电磁暂态多速率仿真,并兼顾不同时间尺度系统的计算精度。同时,解决了自动建模、高精度初始化、全状态观测等应用问题,推进大电网全电磁暂态仿真的实用化。

最后,通过超大规模电网算例的测试和实际电网录波与仿真结果的对比,验证了所采取技术路线的可行性和所开发产品性能的优越性。

新一代高性能电磁暂态仿真平台在集约化的硬件平台上全面提升了电磁暂态仿真的性能。随着计算机技术和电磁暂态理论的发展和完善,还有进一步的提升空间。未来可应用于基于在线监测数据的全电磁暂态超前预测,并能为数字孪生电网的实现提供技术支撑。

同时,在自主开发过程中还需要注意以下几点:一是高性能电磁暂态仿真产品的研发不只是对电磁暂态仿真理论和算法的简单实现,而是融合电力系统和计算机软硬件等多学科的系统性工程,对其研发周期和复杂度应有充分的认识和准备；二是面对国外成熟产品的压力,可着力提升产品的适应性和易用性,开发适应中国新型电力系统仿真需求的本地化功能；三是产品需具备更高的开放性,以满足灵活自定义模型的深层次需求,并能通过丰富的跨平台接口允许用户继续使用已有的模型数据资产和仿真设施,最大程度地发挥产品价值。