均质黄土坝变形计算参数全局敏感性分析
孙一清 黄 天 王桂智 薛宇阳 徐力群方卫华 冯亚新 黄章鑫 金洪杰 崔卫东
(1.河海大学 水利水电学院,南京 210098;2.江苏省水利勘测设计研究院有限公司,江苏 扬州 225127;3.上海市堤防泵闸建设运行中心,上海 200080;4.水利部南京水利水文自动化研究所,南京 210008;5.江苏省东台市自然资源和规划局土地整理中心,江苏 东台 224200)
大坝是水资源管理的重要基础设施,中国有9.8万多座大坝,其中土坝有8万多座.土坝具有对各类环境的高度适应性,并可以在坝址区就地取材,建造方便等优点,因而被广泛采用[1].实际建造过程中,随着坝体施工高度不断上升,土坝工程变形情况及其安全性会随之改变.虽然坝体多采用分层施工的方式,但完工后,大坝整体仍然会因为自重的原因产生相应的位移变化.蓄水期大坝的变形又会在自重与水荷载的共同作用下继续发展,因此对土坝变形分析是十分必要的.
土坝的主体部分多为当地土料,土料具有粒状非连续固体颗粒的特性,在受到自重和水压力作用下会产生变形,通常土体的变形分析采用非线性有限元法进行计算,其中邓肯-张E-B模型是最常用的材料本构模型之一[2-5].邓肯-张E-B模型参数通常可以根据已建造工程的经验类比得到,但这样得到的参数往往精度不够,随着施工技术的发展,后来逐步演变为由室内、室外三轴试验测得,但测得的参数多与实际岩体参数有较大的偏差[6-7].实践表明,不管使用何种非线性模型,都必须有足够精确的参数,否则无法达到理想的效果.可见,如何准确、便捷、合理地获得土料的邓肯-张E-B模型参数,减少大坝设计施工过程中的工作量是进行土坝变形分析时需要解决的关键问题[8].如今大坝参数大都需要通过算法将参数反演问题转化为一个优化问题来获取,但这需要大量的试验数据来为算法的训练集提供支撑.
近年来,正交试验法作为一种可代替全面试验的便捷、科学的试验方法被广泛运用于工程中[9-13],例如王瑞骏等[10]以公伯峡水电站面板堆石坝作为研究对象,利用正交试验设计对模型参数进行研究,为流变模型参数的选取提供支撑.张文兵等[11]针对大坝热-流耦合模型,运用正交试验设计研究各参数对温度场的影响,发现渗透率和土体比是模型中的重要参数.李炎隆等[12-13]基于正交试验法,分别研究了堆石料模型参数对堆石体变形和超高镶嵌面板堆石坝高模量区模型参数对坝体沉降、面板挠度及顺坡向应力的影响.目前,应用到大坝工程的正交试验法多是不考虑交互作用的,仍属于局部敏感性分析的范畴,而实际工作中,各因素之间的关联对于目的指标的影响是不能忽视的;除此之外,由于邓肯-张E-B模型中参数众多,标准正交表的列数无法同时容纳所有邓肯-张E-B模型中参数及参数之间的交互作用列,因此有必要对大坝变形影响不显著的邓肯-张E-B模型参数进行筛选.本文以某均质黄土坝为例,建立有限元模型对大坝变形进行模拟,并通过Plackett-Burman试验设计对邓肯-张E-B模型中参数进行显著性筛选,再用正交试验对筛选参数进行全局敏感性分析,研究参数及参数交互作用下对土坝变形的敏感性排序.以期为均质土坝邓肯-张E-B模型参数选取提供参考.
1 邓肯-张E-B模型原理
通常均质黄土在数值计算中的应力应变关系是非线性的,邓肯-张E-B模型即为其中之一[14].
根据变形模量的定义,可得切线模量Et为:

式中:Rf为破坏比;S为剪应力比;Ei为初始剪切模量.

式中:σ1为大主应力;σ3为小主应力.

式中:pa为标准大气压;K、n可由试验确定.
根据摩尔-库仑破坏准则有:

式中:c为黏聚力;φ为内摩擦角.
将S、Ei分别代入式(1),得切线模量表达式为
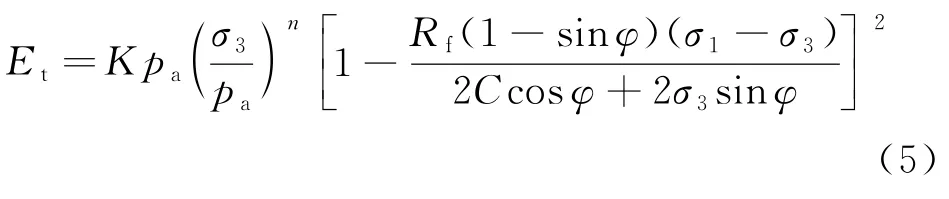
2 敏感性分析方法
邓肯-张E-B模型共有10个计算参数c、φ、Δφ、Rf、K、Kb、n、m、Kur、nur.实际研究中,并不会选择全部参数来研究其对大坝变形的敏感性分析,由于坝体处于压实状态且为散粒体,故Kur、nur、C不参与讨论,除此之外将坝料密度ρ纳入考虑范围.
实际研究中发现,各因素的变化不仅会对目的指标产生影响,而且其相互间的联动也会对目标指标产生影响,在试验设计中称这种联动为交互作用,有时不同因素相互间的联动对于目的指标的影响可能会超越因素本身.交互作用主要通过因素联动的数量来区分:一阶交互作用主要发生在任意两个因素之间,高阶交互作用通常发生在3个或者3个以上的因素之间.通常在考虑交互作用的全局敏感性分析中,高阶交互作用对于目的指标的显著性影响微乎其微,一般只研究少数因素的一阶交互作用.正交试验通常也只需考察两两因素之间的交互作用,而现有的标准正交表所考察的列数无法同时满足八个计算参数以及八个参数两两之间的交互作用,因此需要使用Plackett-Burman试验设计筛选出更为显著的参数,以科学合理地减少正交表所需要的列数,随后再进行考虑交互作用的正交试验.
由于极差分析法具有一定的局限性,不能区分试验结果的差异具体是由什么因素引起[15].本文使用的两种试验设计方法的结果均采用方差分析法,具体原理如下:

式中:ST为总离差平方和;Si为第i个因素的离差平方和;Se为误差的离差平方和;k为因素i在水平j下重要试验的次数为因素i在水平j下重复试验的第g次所对应的试验结果,{|i∈(1,m),j∈(1,r),g∈(1,k)}.其中
df为各因素自由度,dfT、dfi、dfe分别表示ST、Si、Se的自由度.
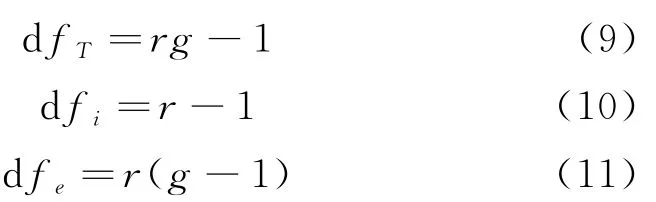
各因素的均方为:

误差的均方为:

检验敏感性统计量F值为:

若Fi≥F0.01,说明该因素非常显著,记为**;若F0.01>Fi>F0.05,说明该因素显著,记为*;若F0.05≥Fi≥F0.1,说明该因素有影响,记为⊙;若F0.1>Fi>F0.2,说明该因素有一定影响,记为Δ;若F0.2≥Fi,说明该因素无影响.
2.1 Plackett-Burman试验设计方法
Plackett-Burman试验设计主要被运用于多个因素的筛选,该方法旨在从多个未知其对于目的指标影响强弱的因素中,筛选出对目的指标影响显著的,以便后续的研究.在多个因素中,每个因素取高低两个水平,通过试验设计表格研究因素高低变动对于目的指标变动的影响.通过确定影响显著的因素,达到筛选因素的目的,相应地减少后续研究中的工作量,因此,Plackett-Burman试验设计被广泛应用于实际工作中,起到了很好的效果.
Plackett-Burman试验设计按规则生成,排列可具有不唯一性,对于N次实验至多可研究(N-1)个因子,但实际因子应该不多于(N-4)个,保留3个以上虚拟变量用以估计试验误差.其试验次数N为4的倍数,但N为2的幂的时候除外.常用的N为N=12、20、24、28、36等.
2.2 正交试验设计方法
正交试验设计属于试验设计方法的一种,根据是否考虑因素间的交互作用可划分为两类.不考虑交互作用的正交试验属于局部敏感性分析方法,而考虑交互作用的正交试验属于全局敏感性方法.不管是哪种正交试验设计,都需正交表的参与,正交表用Ln(rm)表示,试验的目标因素称为目标指标.标准正交表如图1所示.每张正交表都是通过正交原理设计出的标准化的试验安排表格,具有科学性和均匀分布的特点,可涵盖所有的试验情况,如L8(27)、L16(215)等.

图1 标准正交表
3 工程实例
3.1 位置描述
某水库位于黄土中山丘陵区,该库大坝全长575 m,坝顶高程1 557 m,最大坝高96 m,防浪墙顶高程1 558.2 m,水库正常蓄水位1 554 m.水库总库容为4587×104m3.大坝河床段典型横剖面图如图2所示.

图2 河床段典型横剖面图
3.2 水库大坝有限元模型
计算坐标系规定为:将河流走势方向定义为X轴,沿河流走势方向指为正向,取计算模型最左下为X轴零点;将坝轴线方向定义为Y轴,由大坝右岸指向左岸为正向,取右岸坝轴线端为Y轴零点;将垂直方向定义为Z轴,上方为正向,模型底部高程1 266 m为Z轴零点.
计算模型的边界范围:下边界从大坝建基面向下取200 m,即从大坝建基面高程1 466 m处再垂直向下取两倍坝高作为地基,地基厚度约为200 m;上游边界从大坝上游坝脚处向X轴负坐标方向取1.5倍坝高,约为150 m;下游边界从大坝下游坝脚处向X轴正坐标方向取1.5倍坝高,约为150 m.
底部约束有限元模型的地基下方,位移约束分别约束地基x方向两侧与y方向两侧.坝体典型断面有限元网格如图3所示.

图3 典型断面有限元网格
3.3 计算参数
坝体黄土与风化泥岩混合料、排水反滤层、开挖翻填料、开挖压重等各料区土料的本构模型采用邓肯-张E-B模型.坝体各料区的计算参数见表1.由于水库黄土均为湿陷性黄土,施工前会发生深厚覆盖层渗漏及不均匀变形问题,经处理后的坝址区具备建坝条件.

表1 坝体填筑材料计算参数(邓肯-张E-B模型)
3.4 分级加载
大坝建造全部共有18级加载完成坝体填筑和蓄水.分级加载及蓄水过程如图4所示.
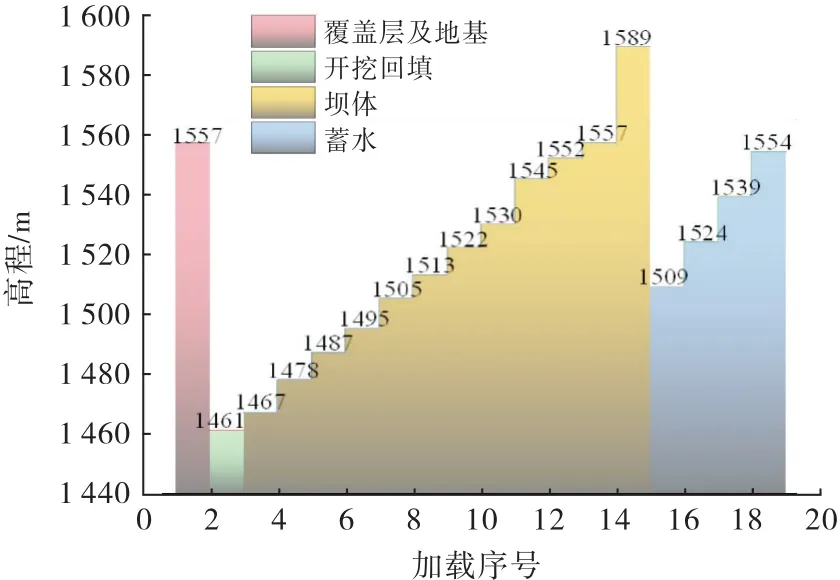
图4 有限元计算分级加载及蓄水过程
3.5 数值模拟结果
计算时,首先加载基岩和未清除的覆盖层,并在分级加载坝体之前将结点位移初始化为零,仅保留单元应力,从而获得地基初始应力场.下文所述的位移均是指开始施工填筑以后的位移.
通过数值模拟计算大坝竣工期及运行期坝体典型断面位移分布如图5所示.具体数值模拟计算成果见表2.

图5 典型断面位移分布

表2 堆石体位移二维计算分析结果汇总 (单位:mm)
整体来看,该坝的变形分布符合一般土石坝的分布特点,竣工期坝体水平位移呈对称分布,运行期坝体蓄水后,在上游水压力的缓慢作用下,水平位移分布规律由对称分布逐渐向下游变形,竖向位移呈现均匀下降趋势,最大值在坝体2/3处,运行期最大竖向位移略大于竣工期最大竖向位移.竣工期和蓄水期坝体竖向位移分别约占最大拔高的1.01%和1.03%,分析原因可能是当地黄土为湿陷性黄土所致.
4 敏感性分析
4.1 Plackett-Burman试验设计方法
对φ0、Δφ、Rf、K、Kb、n、m参数进行 Plackett-Burman试验设计,目的指标分别为竖向位移V、向下游水平位移H1和向上游水平位移H2.7个参数作为7个因素,每个因素考察低(-1)和高(+1)两个水平,其中低水平为设计参数的80%,高水平为设计参数的120%,见表3.

表3 Plackett-Burman试验因素水平
为保证筛选试验的准确性,实验设置一列误差列,同时保证足够的试验次数便于分析出7个参数的显著性程度,因此设计出一个需试验24次的Plackett-Burman试验方案,具体见表4.

表4 Plackett-Burman试验方案表
表格中试验顺序是随机的,目的是减少试验中由于先后不均匀带来的误差干扰,进一步确保筛选的准确性.将φ0、Δφ、Rf、K、Kb、n、m分别填入试验方案表的第2、3、4、5、6、7和8列;将竖向位移、向下游水平位移和向上游水平位移分别填入试验方案表的第10、11和12列,表中第9列作为误差列.
结果分析见表5.可以看出,各参数关于竖向位移V的敏感性程度由高到低依次为Rf>Kb>φ0>K>n>Δφ>m,其中对于竖向位移明显显著的是Rf、Kb和φ0,有一定影响的是参数K,而n、Δφ和m3个参数对于竖向位移均为无影响.各参数关于向下 游水平位移H1的敏感性程度由高到低依次为Rf>φ0>Kb>K>Δφ>n>m,其中对于向下游水平位移 明显显著的是Rf、φ0和Kb,而K、Δφ、n和m4个参 数对于向下游水平位移均为无影响.各参数关于向上 游水平位移H2的敏感性程度由高到低依次为Rf>φ0>Kb>K>n>Δφ>m,其中对于向上游水平位移 明显显著的是Rf、φ0、Kb,显著的是K,而n、Δφ和m3个参数对于向上游水平位移均为无影响.
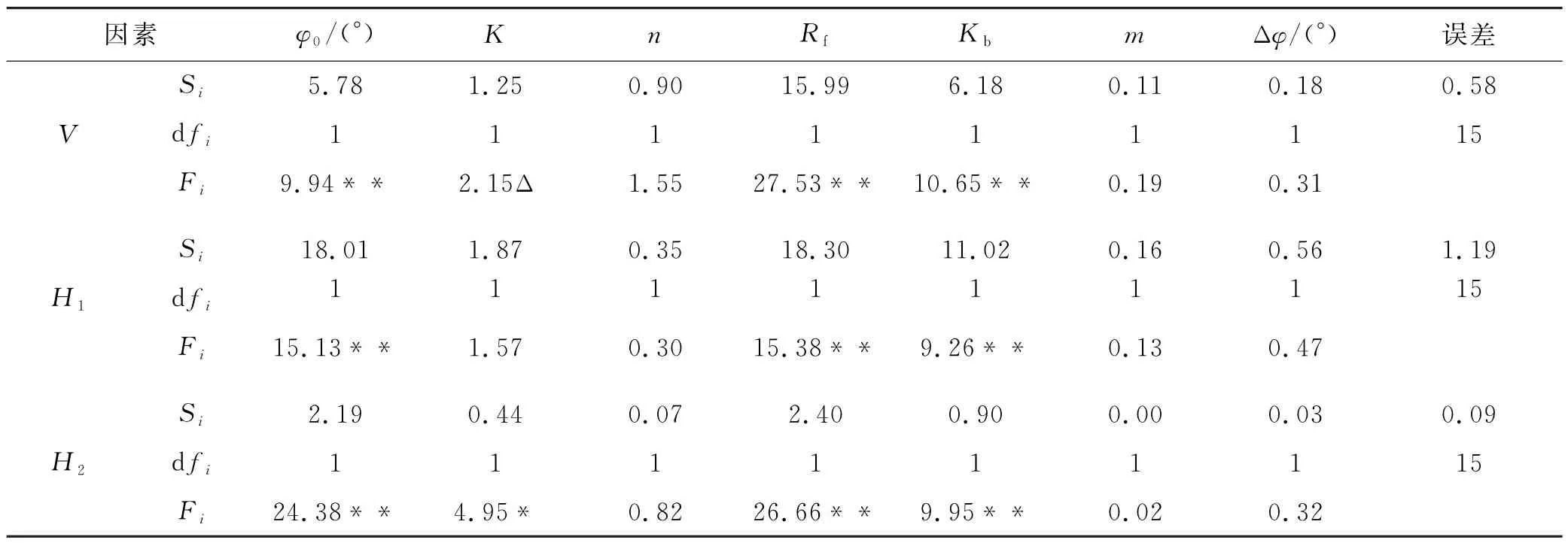
表5 Plackett-Burman试验分析结果
综合来看,Rf、φ0、Kb和K4个参数对于黄土均质坝变形的影响更加显著,这与文献[12]得到的结论一致,计算参数需要重点考虑的参数为Rf、φ0、Kb和K,而参数Δφ、n和m对于变形的影响基本可以忽略不计,因此在考虑一阶交互的正交试验中,只考察Rf、φ0、Kb和K的敏感性.
4.2 考虑交互作用的正交试验
在上述Plackett-Burman试验设计的基础上,对Rf、φ0、Kb和K4个参数进行考虑交互作用的正交试验.目的指标分别为竖向位移、向下游水平位移和向上游水平位移.Rf、φ0、Kb和K4个参数分别作为4个因素,每个参数考察低(-1)和高(+1)两个水平,其中低水平为设计参数的80%,高水平为设计参 数的120%.具体因素和各因素水平见表6.
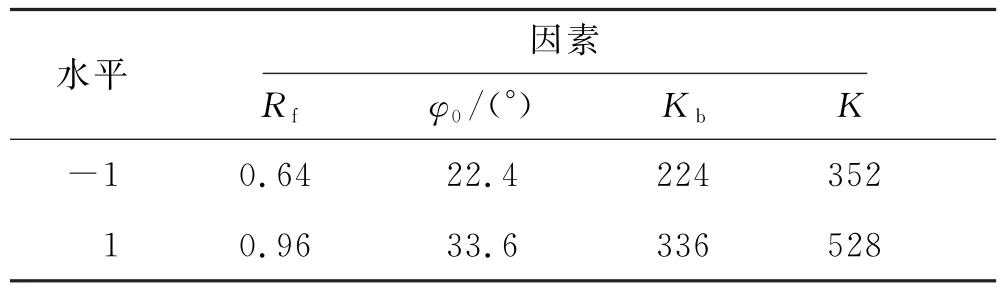
表6 正交试验因素水平参数取值
由于不仅要考虑上述4个参数的敏感性,还需要考虑Rf×φ0、Rf×Kb、Rf×K、φ0×Kb、φ0×K以及Kb×K的敏感性.因此选择能够容纳4因素及其交互作用的表头设计.L16(215)表的交互作用见表7.

表7 L 16(215)表头设计
选择正交表时,由于需考虑4个参数,选择4因子表头,将Rf、φ0、Kb和K分别填入表头中第1、2、4和8列,将Rf×φ0、Rf×Kb、φ0×Kb、Rf×K、φ0×K以及Kb×K分别填入表头中3、5、6、9、10和12列,因此选用能容纳12因素2水平的正交表,其中第7和11列可作为误差列.
除了考虑因素水平外,还需要保证对精度的要求,试验次数越多,试验精度越高.故本次考虑交互作用的正交试验选择L16(215)的正交表.具体试验方案 及有限元计算结果见表8.

表8 正交试验方案及变形结果
对上表中数据及结果进行方差分析,结果见表9.关于竖向位移V的敏感性程度由高到低依次为Rf>Kb>φ0>Rf×Kb>φ0×Kb>K>Rf×φ0>Rf×K>Kb×K>φ0×K,其中Rf、Kb和φ0明显显著,Rf×Kb、φ0×Kb、K、Rf×φ0和Rf×K显著;关于向下游水平位移H1的敏感性程度由高到低依次为Rf>φ0>Rf×φ0>Kb>Rf×Kb>φ0×Kb>K>Rf×K>φ0×K>Kb×K,其中Rf、φ0、Rf×φ0、Kb、Rf×Kb和φ0×Kb明显显著;关于向上游水平位移H2的敏感性程度由高到低依次为Rf>φ0>Rf×φ0>Kb>Rf×Kb>φ0×Kb>K>Rf×K>φ0×K>Kb×K,其中Rf、φ0、Rf×φ0、Kb、Rf×Kb、φ0×Kb和K明显显著.综合来看Rf、Kb和φ0是对大坝变形敏感性最强的3个参数,三者对于大坝变形的敏感性均强于参数K,考虑其交互作用时,Rf×φ0、Rf×Kb以及φ0×Kb之间的交互作用对于大坝变形的敏感性是不可忽视的.

表9 正交试验方差分析
5 结 论
为研究邓肯-张E-B模型参数对于大坝变形的影响,本文以某均质土坝作为研究对象,通过建立静力分析模型,分析大坝运行期和竣工期的基本变形规律,并借助Plackett-Burman试验设计和正交试验设计对邓肯-张E-B模型参数进行敏感性分析.得到如下主要结论:
1)由于坝址区主要存在黄土湿陷、深厚覆盖层渗漏及不均匀变形问题,经处理后的坝址区具备建坝条件.土坝的变形分布规律满足一般土石坝的分布特点.
2)通过Plackett-Burman试验设计对7个邓肯-张E-B模型参数进行研究,可以发现,从单个因素对于土坝变形的影响来看,7个计算参数中Rf、φ0、Kb和K4个参数是对于大坝变形明显显著的参数.
3)使用正交试验设计对Rf、φ0、Kb和K这4个参数以及4个参数之间的一阶交互作用进行全局敏感性分析,分析结果表明,Rf、Kb和φ0是对大坝变形敏感性最强的3个参数,三者对于大坝变形的敏感性均强于参数K,而Rf×φ0、Rf×Kb以及φ0×Kb之间的交互作用对于大坝变形的敏感性是不可忽视的,甚至其交互作用的敏感性大于单个参数的敏感性.
4)综上可知,对均质黄土土坝邓肯-张E-B模型参数的全局敏感性分析是十分必要的,本文研究内容可为土坝变形计算参数的选择提供一定的参考,但是否可以推广到其它级配及物理特性的土坝,需要进一步验证.

