基于MLPG无网格法的土石坝非稳态饱和渗流场分析

郑保敬 邹申威 雷 未 叶 永

(三峡大学 水利与环境学院，湖北 宜昌 443002)

渗流自由面作为渗流边界的一部分，它的位置事先是未知的，并且随着上游水位的变化而变化，因此该类问题属于动边界问题.解决此类问题的数值方法一般采用迭代法.渗流自由面的确定往往依赖于网格划分的有限元法，其中网格按动态性质分为固定网格和移动网格两大类[1].固定网格在系统迭代处理过程中，网格形状始终保持不变，根据研究内容的差异性，又衍生出不同固定网格法，如耦合单元法、虚位单元法、初位流量法和剩余流量法等.而移动网格法在渗流迭代计算过程中，通过不间断动态调整网格位置来自适应渗流自由面位置，直至满足最小二乘数的控制误差.该系统求解方法同样依赖移动网格的频数，每一次模型迭代都将重新划分网格，造成计算过程复杂冗长的问题.在解决动边界问题时，无网格法可摆脱网格的限制，只需通过一组离散节点来构造形函数，具有处理方便、布置灵活的特点，可有效摆脱有限元对网格过分依赖的局限性[2-4].

无网格法的研究始于上世纪七十年代光滑粒子流体动力学(SPH)方法的提出.随后许多学者对无网格法进行了研究，发展至今已经形成了很多种方法，包括再生核粒子法(RKPM)，无单元Galerkin法(EFG)，有限点法(FPM)，复变量无网格法以及基于边界积分方程的无网格法[5]等.1998年Atluri等[6]首次提出了无网格局部Petrov-Galerkin法(MLPG)，该方法在构造模型形函数和数值积分上均不需要网格作为求解基础，是真正意义上的无网格法.

近几年，有部分学者将无网格法运用至饱和土体的稳态渗流问题上.如李树忱等[7]对模型重心采用基于拉格朗日原理的配点插值无网格法，来模拟稳态下的渗流自由面问题;陈锐等[8]通过比较自适应节点与静态均匀节点在无网格法下的数值解和解析解误差，从而提出一种节点可自适应化无网格法;唐雄等[9]通过无网格法中的物质点法(MPM)探究了大变形岩土工程问题和多相流问题，发现模型计算所得的数值解和理论解吻合度很好，且多相物质配点法能够较为准确表述非饱和场的孔隙介质渗流特征和饱和场的孔隙介质水力特征;杨悦[10]提出将边界积分方程与最小二乘法相结合来求解定解问题的微分方程，通过编制Matlab程序求解变系数渗流问题，该方法不仅节点布置灵活，还能有效避免因奇异矩阵对模型精度的影响.目前无网格法在土石坝非稳态渗流问题的研究相对较少，本文采用基于滑动Kriging插值的无网格局部Petrov-Galerkin法[11]求解水位变化情况下土石坝的稳态和非稳态渗流问题.该方法利用滑动Kriging插值法构造近似函数，使算法具备Kronecker函数特性，并直接赋予本质边界条件，将Heaviside分段函数看作权函数，使得转化的积分方程只剩边界积分部分，从而减少计算量，最后采用数值算例对该方法的有效性进行验证.

1 二维土石坝非稳定饱和渗流问题

考虑一均质土石坝，如图1所示在渗流饱和区域Ω内任意一点A的水头h为

图1 土石坝非稳定渗流模型

式中:y为A点垂直坐标分量;p为孔隙水压力;γw为水的重度.

符合达西定律的二维非稳定饱和渗流问题的控制方程可以表示为

不规范处方主要包括：①处方超量，如普通处方超过7天量，急诊处方超过3天量，省特约处方超过7天量，无特殊治疗需要处方超过1个月用量等；②临床诊断书写不全、病人信息不全；③医生输入错误；④医师处方未签名（盖章）或与留样不一致；⑤处方上药品品种数量超过规定（5种）；⑥处方修改未签名盖章，也未注明修改日期；⑦处方用笺不规范，如门诊手写处方用的是住院处方或自费药房处方。

边界条件:

初始条件:

式中:kx和ky分别为沿x和y方向的渗透系数;Ss=ρg(α+nβ)为单位贮存率;ρ为水的密度;α为土料的体积压缩系数;n为孔隙率;β为水的压缩系数;μ为给水度，表示为饱和土体含水层自由面其单位截面积吸收或释放最大水量与土体总体积比率;θ为自由面外法线方向与竖直方向的夹角.

2 二维非稳定饱和渗流问题的MLPG无网格法

2.1 滑动Kriging插值形函数

Kriging插值方法采用无偏估计和线性回归模型，类似于移动最小二乘法(MLS)，该加权为近似可连续的移动，所以称为滑动Kriging插值法.定义在问题域Ω及其边界Γ上的场函数为h(x)，将系统求解域离散为N个场节点分布，且空间内任意点x的局部支持域又含n个场节点，若已知节点的场函数值为h(x1)，h(x2)，…，h(xn)，则点x处的场函数值可以通过已知节点的场函数值来逼近

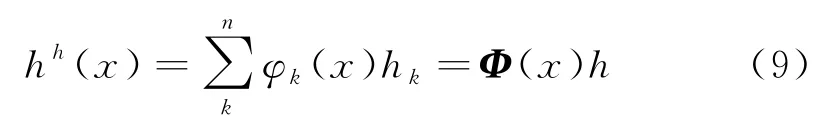
式中:Φ(x)=[φ1(x)，φ2(x)，…，φn(x)]为通过滑动Kriging插值法构造的形函数，表达式为

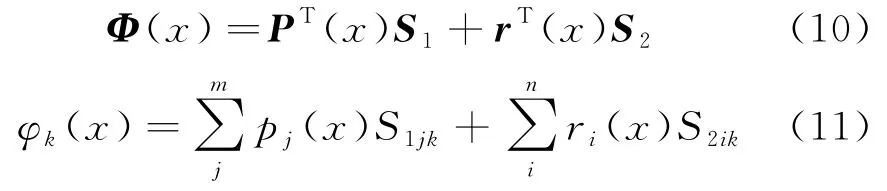
式(10)中S1和S2分别为

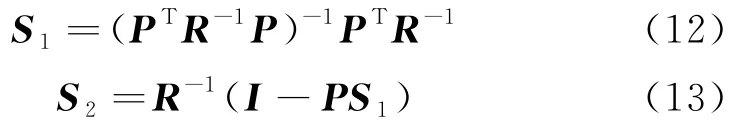
式(12)与(13)中PT和R分别为

式(14)～(16)中:PT(x)为多项式基函数;R[R(xi，xj)]为对角线为1的对称相关矩阵;R(xi，xj)为节点xi与xj之间的相关函数，通常取Gaussian型函数.

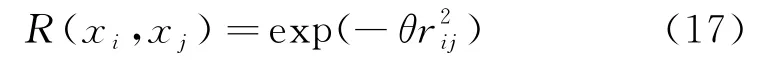
式中:θ＞0，为模型参数;rij为节点xi与xj之间的距离.

2.2 非稳态饱和渗流问题的MLPG法

采用N个场节点将整场渗流域Ω与边界域Γ进行离散化处理，局部支持域内的任意点I选择加权余量法近似求解，式(2)的积分弱形式为

式中:wI为与节点I对应的权函数;Ωq为与节点I对应的局部子域.

当考虑求解域Γ与局部积分域边界Γq重叠时，Γq(Γq=Γqi+Γqt+Γqu)由以下3部分构成:Γq与Γ不重叠，记为Γqi;Γq与自然边界重叠区域，记为Γqt;Γq与本质边界重叠区域，记为Γqu.对式(18)引入自然边界条件，并令Ss=0可得

在非稳态渗流问题中，系统内场节点的物理函数随空间域和时间域的改变而变化，其关系可近似为

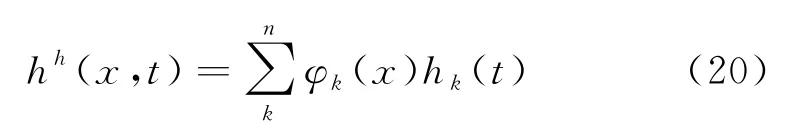
式中:φk为形函数;hk为给定的节点处的函数值.

将式(20)代入式(19)中得到节点I的离散系统方程为

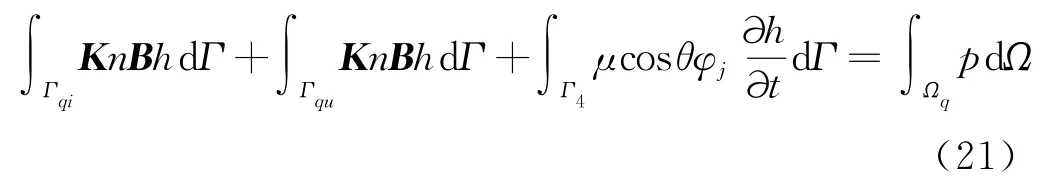
式(21)的矩阵形式为

式中:

将所有编号的各节点按顺序依次代入离散控制方程进行集合，从而得到总体控制方程式为

对于时间域的离散，本文采用向后差分格式

代入总体系统方程为

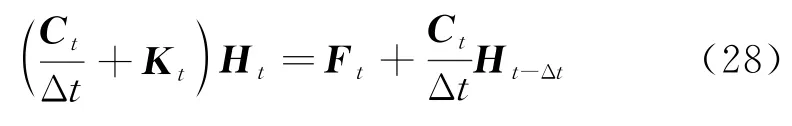
3 数值算例

3.1 稳定渗流

例1:考虑如图2所示的矩形均质土石坝，坝高为8 m，宽为4 m，上游水位6 m，下游水位1 m，土体渗透系数为k=0.016 m/d.假定第一类边界条件:HΓ1=6.0 m，HΓ2=1.0 m，Γ5为潜在溢出面边界.第二类边界条件:Γ3为不透水边界，Γ4无流量补给.

为了验证初始自由面对迭代计算结果的影响，分别假设3条初始自由面如图2所示，各初始自由面的求解域如图3所示.

图2 矩形土坝渗流模型(单位:m)

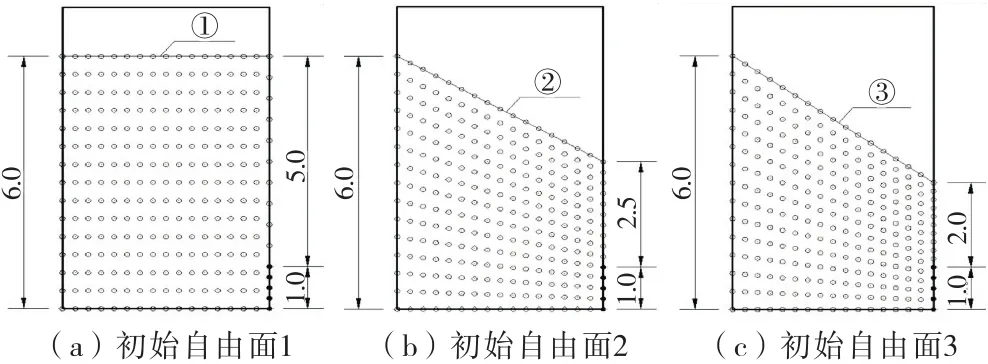
图3 场节点布置示意图(单位:m)

在每个区域内均布置255(17×15)个节点，计算结果的绝对误差取0.001 m.表1给出了不同数值方法所计算的自由面上的水头值，从表1中可以看出本文方法计算的结果和实验误差最小，而且本文方法对初始自由面的位置不敏感，通过迭代都能很快收敛到最终自由面的值.

表1 自由面上典型参考点在不同计算方法下水头值比较 (单位:m)

3.2 非稳定渗流

例2:文献[13]中介绍的均质土坝实验模型，将砂坝盛放在一个能调节两端水位的水槽中，对不同速度水位上升和水位下降工况下的实验结果与数值计算结果进行比较:下游水位稳定在10 cm，上游水位由10 cm 在不同时间段(30、60、120、240、600、4 800 s)均匀上升至30 cm变化情况，计算结果与实验结果如图4所示;上游水位稳定在30 cm，下游水位由30 cm在不同时间段(30、60、120、240、600、2 400 s)均匀下降至10 cm变化情况，计算结果与实验结果如图5所示.数值计算条件与模型试验相同，初始时刻求解区域内均匀布置5 151(101×51)个节点，时间步长取0.5 s.

图4 水位上升时数值与实验结果比较示意图

图5 水位下降时数值与实验结果比较示意图

由图4～5可知，在不同速度水位上升和水位下降工况下，本文方法计算的渗流自由面位置与实验结果均较为吻合，表明对非稳定渗流问题采用MLPG法是有效可行的，且满足精度要求.

例3:图6为质梯形坝示意图，坝高17 m，顶宽6 m，底宽91 m，假设上游初始水位H1=15 m，并以匀速下降至H′1=5 m，下游水位为H2=2 m.梯形坝的贮水率为Ss=0，饱和渗透系数为k=0.861 m/d，给水度为μ=0.006.梯形坝求解区域内均匀布置2 852(92×31)个节点，时间步长取0.01 d.图7为上游水位在不同高度时按稳态渗流问题计算得到的自由面位置，图8和图9分别为上游水位下降速度为0.1 m/d和1 m/d时的计算结果.

图6 均质梯形坝示意图

图7 不同水位下坝体稳定渗流自由面示意图

图8 v=0.1 m/d自由面变化示意图

图9 v=1 m/d自由面变化示意图

从图中可以看出，当上游水位下降速度很缓慢时瞬态结果和稳态结果非常接近;而当上游水位下降速度较大时自由面出现滞后现象，且后期水位在上游坡面的出渗点高于初始水位，从而造成涌水倒流现象，这种现象也符合工程实际情况.

4 结 论

本文采用MLPG无网格法求解均质土石坝的非稳态饱和渗流问题，该方法使用满足狄里克莱函数性质的滑动Kriging插值法构造形函数，对模型可直接施加本质边界条件;Heaviside分段函数作为权函数时，系统内刚度矩阵只需计算边界积分，不需计算区域积分，大幅提高了计算效率.数值算例结果表明本文方法计算的渗流自由面最终位置与初始自由面的设置无关，只在迭代次数上有差异，因此本文方法具有良好的稳定性，适用于求解动边界问题.