混凝土Ⅰ型裂缝失稳扩展时临界有效缝长的数值研究

郑 轶 王向东 刘庆辉

(河海大学 力学与材料学院，南京 211100)

混凝土是由水泥、砂、骨料、水等材料组成的复合材料，在实际工程中混凝土结构难免会出现宏观裂缝，而其损伤和断裂特性对工程安全起着关键作用.因此，准确把握混凝土的破坏机理，确定合理的混凝土断裂参数，对评价混凝土结构的稳定性和安全性具有重大意义，对此，国内外学者进行了大量研究工作[1-8].混凝土材料作为一种准脆性材料，其断裂特性区别于金属材料，在结构承受荷载作用后，宏观裂缝尖端存在一个微裂纹区，即断裂过程区，结构失稳断裂时，宏观裂缝已经有了一定的扩展，大量研究表明引入断裂过程区的影响[9-10]是必要的.

文献[11]对混凝土裂缝失稳扩展临界有效裂缝长度进行了研究，即通过实验和数值模拟的方法对测定的F-δ(荷载-位移)曲线，采用柔度改变法测得有效裂缝缝长，该方法得到的临界有效缝长，结果是合理的，但是断裂过程区的存在对裂缝扩展的影响必须从断裂和损伤力学理论的角度进行研究，一方面使研究结果更具科学理论依据支撑，另一方面考虑损伤对裂缝扩展的影响更符合实际情况.

本文在文献[11]的基础上，从断裂与损伤耦合的角度，推导出计算混凝土Ⅰ型裂缝失稳扩展临界有效裂缝长度的新方法，并通过数值模拟实验，对计算结果进行对比分析，进一步计算失稳断裂韧度，与传统计算方法和文献[11]计算方法进行对比，以验证推导方法的可行性并且说明考虑混凝土宏观裂缝前端微裂纹区的断裂与损伤对断裂韧度的影响是有必要的.

1 基于虚拟裂缝模型和最大拉应变断裂判据的有效缝长

1.1 虚拟裂缝模型概述

1976年，Hillerborg等[12]在塑性力学模型的基础上提出了虚拟裂缝模型(FCM).该模型认为宏观裂缝扩展前，在裂缝前端已出现微裂缝区.在此区域内，材料刚度降低，从而削弱了该区域传递应力的能力.但微裂缝区内仍有骨料相连或基体粘结，因此微裂缝区域内传递应力能力并未完全丧失，这部分传递的应力称为黏聚力.通过分离式裂缝的表征方法将微裂缝区定义为“虚拟裂缝区”，也叫断裂过程区(FPZ).

对于Ⅰ型裂缝，断裂过程区可表示为黏聚力σ与裂缝张开位移w之间的关系，图1即在断裂过程区内黏聚力随着位移逐渐张开而变化的软化本构关系.

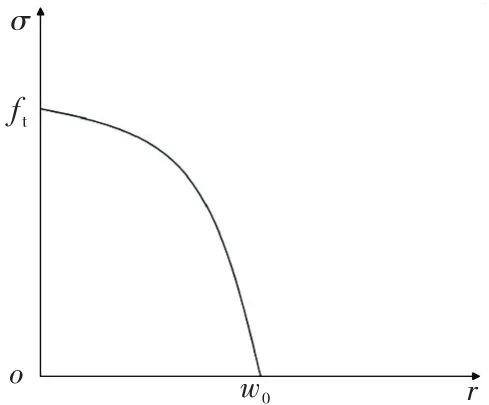
图1 应力软化曲线

由图1可知，当裂缝张开位移w为0时，相应微裂缝区域内的黏聚力等于混凝土抗拉强度;当裂缝张开位移w达到临界值w0时，对应微裂缝区的黏聚力降为0，此时裂缝区域的虚拟裂缝面不再传递应力.

1.2 有效裂缝缝长a c的计算

依据断裂力学，可得Ⅰ型裂缝尖端应力场公式:

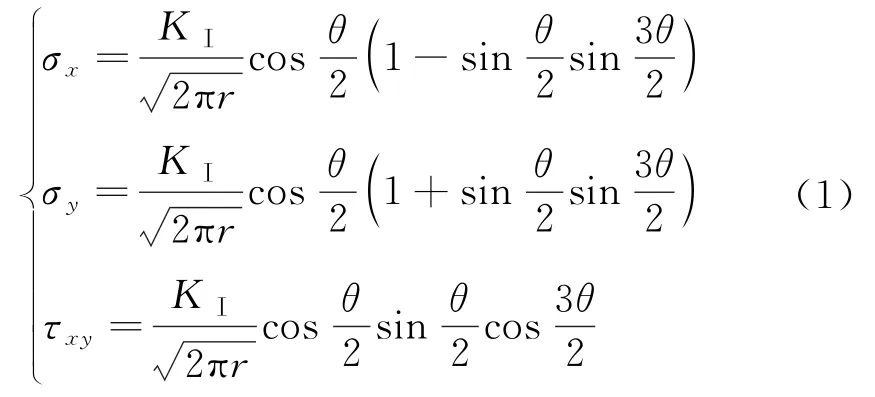
式中:σx、σy、σz为裂缝尖端区域的应力;KⅠ为应力强度因子;r、θ为极坐标.

当混凝土处于失稳扩展临界状态时，依据虚拟裂缝模型，在靠近裂缝端部区域内的混凝土沿着裂缝线方向，有一部分微裂缝区域内黏聚力为零，裂缝张开位移w≥w0，因此可将这一区域等效为混凝土的软化开裂区域，如图2所示，r0即为软化区域，该区域的长度即可等效为混凝土临界有效缝长的增加量Δac.

图2 裂缝尖端区域应力变化情况

由于混凝土是准脆性材料，依据最大拉应变断裂判据，当裂缝尖端最大拉应变达到极限应变时，裂缝将开始扩展，由胡克定律可得到相应的应力表达式:

式中:σr为相当应力;σb为极限应力，σ1、σ2、σ3为主应力;v是泊松比.

根据主应力公式，由式(1)可得缝端的主应力为:

在平面应力状态下，将式(3)代入式(2)，对于混凝土Ⅰ型裂缝，取混凝土的极限应力σb轴向抗拉强度为ft，并代入(2)，在裂缝线上(θ=0)，则有

式中:软化区域r0由于不再传递应力，因此可以将其等效成宏观裂缝有效扩展长度Δac，临界有效缝长为ac=a0+Δac=a0+r0.

2 基于Loland损伤模型和最大拉应变断裂判据的有效缝长

2.1 Loland损伤模型

Loland[13]在对混凝土试验进行研究时发现，当应力即将达到峰值应力前，应力-应变不再是直线关系，这表明当应变小于峰值应变εf时，材料的内部存在着损伤区，当应变大于εf时，材料已经发生严重劣化，应力迅速跌落，损伤不断增大，本文只考虑峰值之前的裂缝尖端混凝土的损伤演化.

常用的混凝土损伤演变方程为:

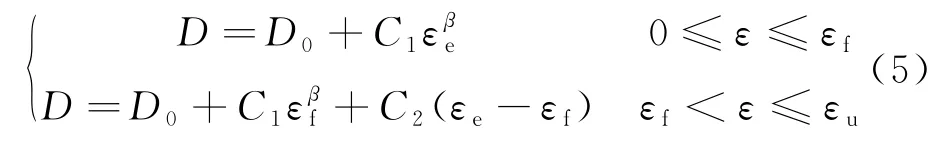
式中:D为损伤;D0为初始损伤;C1、C2和β为材料参数;εf为峰值应力对应的应变;εu为极限应变，ε=εf时，σ=σf，dσ/dε=0，考虑到ε=εu时D=1，得到:

根据文献[11]取混凝土材料的初始损伤变量D0为0.05，根据文献中数据计算得到材料参数β=4.4、C1=7×1016、C2=1935，将求出的材料常数代入损伤演化方程(5)可以得到:

由公式(6)可以得到在峰值前应变与损伤变量之间的关系曲线，如图3所示，随着应变的不断增大，损伤曲线是上升的.

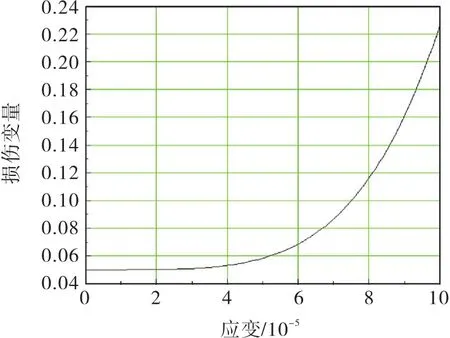
图3 峰值前的应变与损伤变量之间的关系曲线

2.2 双D损伤发展判据

文献[14]中提出了基于损伤和断裂力学耦合的双D发展判据:当裂缝尖端的损伤小于起裂损伤Dini时，缝端损伤处于产生阶段，微裂缝区形成;当裂缝尖端的损伤介于起裂损伤Dini和失稳损伤Dun之间时，缝端损伤处于稳定积累阶段，微裂缝区稳定发展;当裂缝尖端损伤大于Dun时，缝端损伤处于快速失稳发展阶段，微裂缝区发展为宏观裂缝.

描述裂缝尖端损伤发展的判据可以表示为:

当裂缝尖端损伤为Dini时，缝尖端损伤开始稳定积累，此时宏观裂缝处于起裂状态，当裂缝尖端损伤为Dun时，缝端损伤开始快速失稳发展，此时宏观裂缝已经有一定扩展长度Δac.因此，将裂缝尖端的损伤Dini，作为宏观裂缝起裂的标志，即沿着裂缝线扩展方向，缝尖端周围的损伤大于或等于起裂损伤Dini的区域，可以认为其为宏观裂缝区域.

2.3 混凝土Ⅰ型裂缝失稳扩展临界有效缝长

根据最大拉应变断裂判据，裂缝在尖端应变达到最大拉应变时裂缝开始扩展，所以微裂纹出现可以认为是由ε1引起的，微裂纹即为损伤，因此认为损伤也是由ε1引起的.

据胡克定律，由式(3)求得主应变ε1:

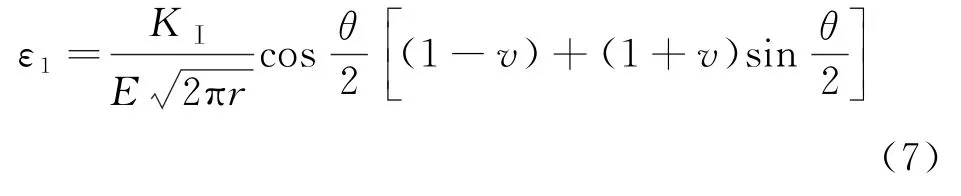
将式(7)中的ε1代入式(5)，可得:

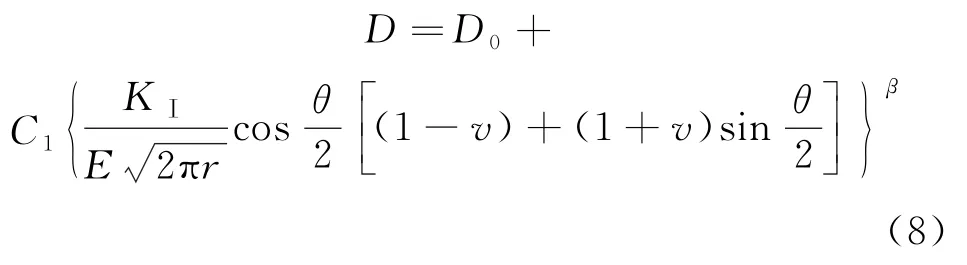
由此可得:

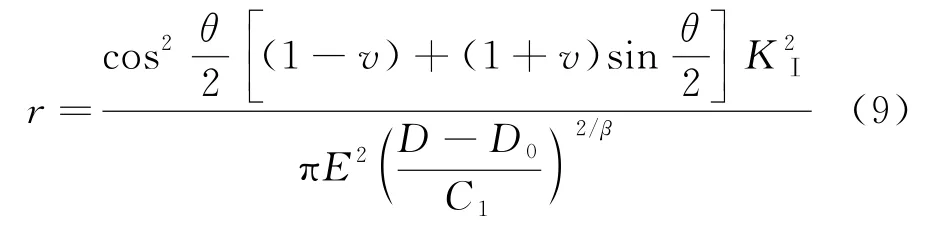
在式(8)中，可以发现，混凝土裂缝尖端的损伤随着r的减小而不断的增大.根据双D判据，当裂缝尖端损伤达到Dini时，混凝土宏观裂缝处于起裂的临界状态，因此，可将Dini作为裂缝起裂的标志，等价于此时宏观裂缝已经开始逐步扩展.而随着荷载的增加，当混凝土裂缝达到失稳扩展临界状态时，原有的宏观裂缝实际上有了一定的扩展，以前述Dini作为宏观裂缝起裂的标志，代入式(9)，可以得到损伤不小于Dini的长度范围，即:

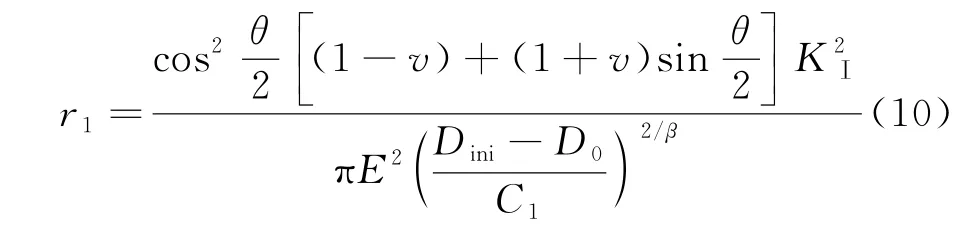
当裂缝失稳扩展时，式(8)反映了裂缝尖端区域沿着裂缝线方向的损伤变化规律.按照双D判据，此时缝尖端的损伤为Dun，在r≤r1范围内，始终有D≥Dini，也就代表这一区域可以等效成有效的宏观裂缝，当r＞r1时，按照式(8)损伤不断减小，且趋于稳定的值，即接近于混凝土初始损伤值D0.对于r＞r1的情况，依据能量守恒定律，损伤总量在等效前后始终保持不变，因此将大于初始损伤的部分损伤等效成某一区域内损伤恒定为Dini时的状态，这一区域长度，如图4所示，即为r2-r1.此时，整个缝尖段区域附近的损伤等效成两部分，一部分长度定义为r2，在这个区域内损伤变量有D≥Dini，在r＞r2区域内，损伤变量保持不变为D0，r2即为等效后的临界有效缝长增量Δac，如图5所示，有效裂缝缝长ac=a0+Δac.由于等效前式(8)函数图像与坐标轴围成面积与等效后函数图像围成面积始终保持不变，如图4所示，S1=S2，所以有:

图4 损伤等效原理图

等效后，混凝土Ⅰ型裂缝失稳扩展时缝尖端损伤示意图，如图5所示.

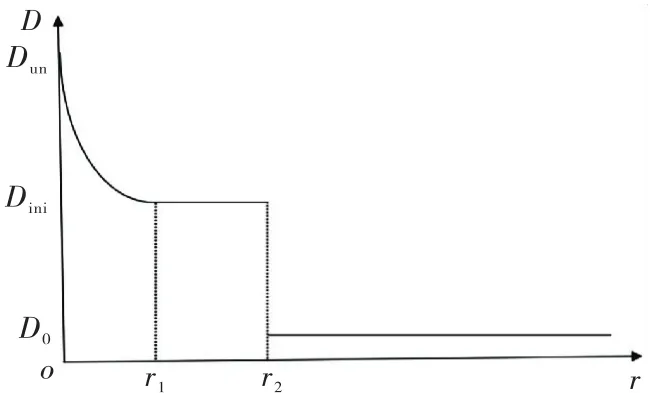
图5 失稳状态时等效损伤示意图

3 Ⅰ型裂缝失稳扩展临界有效缝长数值分析

3.1 试验数据

一般的三点弯曲梁试件跨高比为4，常用试件净尺寸有100 mm×100 mm×400 mm、150 mm×150 mm×600 mm、200 mm×200 mm×800 mm等.试验采用河海系列试验采用的试件[15]，试验试件混凝土基本力学性能参数见表1.

表1 混凝土基本力学性能参数表

Ⅰ型裂缝试件的结构及尺寸为图6所示，有关数据为:初始缝长a0=50 mm，试件宽度b=100 mm，试件高度h=100 mm，试件跨度S=400 mm.

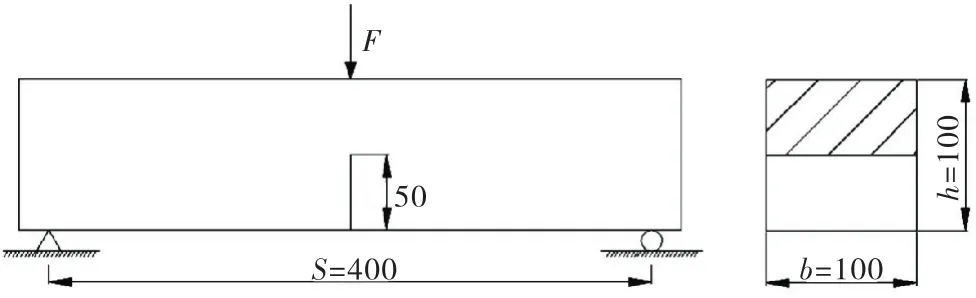
图6 三点弯曲梁示意图(单位:mm)

3.2 模拟计算

基于ANSYS软件平台，对三点弯曲梁试件进行模拟.试件采用的建模方式为先创建关键点，然后关键点连成面，在面上剖分成平面等参4节点单元(PLANE183).再沿着Z方向拉伸成8节点空间等参单元SOLID186，三点弯曲梁的有限元建模以及网格划分如图7所示.

图7 三点弯曲梁有限元网格划分

由文献[11]试验可知，Ⅰ型裂缝的起裂荷载Fini为1 732 N，失稳荷载Fmax为1 820 N.

在起裂荷载Fini作用下，通过有限元计算得到Ⅰ型裂缝试验构件裂缝尖端的应变最大值εini=1.261×10-4，根据式(8)计算得到起裂损伤值为Dini=0.226+1 935×(2.60×10-4-10-4)=0.537.

在失稳荷载Fmax作用下，通过有限元计算得到Ⅰ型裂缝试验构件裂缝尖端的应变最大值εun=1.382×10-4，根据式(8)计算得到失稳损伤值为Dun=0.226+1 935×(2.86×10-4)=0.779.

表2 三点弯曲梁的起裂与失稳情况比较

对于本试验中的Ⅰ型裂缝的损伤断裂行为用双D损伤发展判据可表述为:当混凝土材料的损伤值D≤0.537时，材料是处在材料损伤阶段;当材料的损伤值0.537＜D≤0.779时，材料处于损伤稳定发展阶段;当材料损伤值D＞0.779时，处于损伤失稳发展阶段.

ANSYS计算结果与试验结果比较:

根据试验结果得到外荷载着力点的位移，δ=3.34×10-5m.

将模型的计算结果进行后处理，观察损伤图，如图8～9所示.损伤区形状类似椭圆形，在裂缝两边具有较好对称性，沿裂缝面方向梯度最大，说明裂缝将沿着原方向扩展.

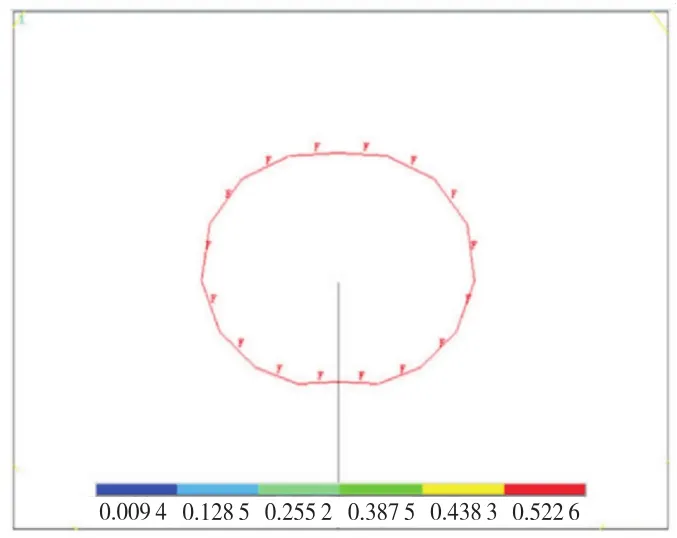
图8 Ⅰ型裂缝起裂荷载下损伤等值线

图9 Ⅰ型裂缝失稳荷载下损伤等值线

根据ANSYS计算得到模型y方向的位移云图，可以读出着力点的y方向的位移即为施加于横梁之上集中力的着力点的位移，节点64的位移δ′=3.14×10-5m.

则其有限元结果与试验结果的误差为:

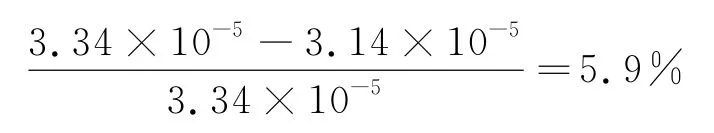
表明该模型的解析结果与实验结果吻合很好，进一步验证了该模型的适用性.

3.3 临界有效缝长及失稳断裂韧度

将试验数据代入式(4)中计算得出Ⅰ型裂缝在失稳临界状态考虑断裂过程区的临界有效缝长ac=a0+r0=56.850 mm.

将试验数据代入式(11)中计算得出Ⅰ型裂缝在失稳临界状态考虑断裂过程区和损伤影响的临界有效缝长ac=a0+r2=56.828 mm.

根据文献[11]中，即课题组之前采用的利用柔度改变法计算得到的考虑断裂过程区的有效裂缝长度ac=57.100 mm，与上述计算所得临界有效缝长结果对比(见表3)，结果基本吻合，验证了计算结果合理性.

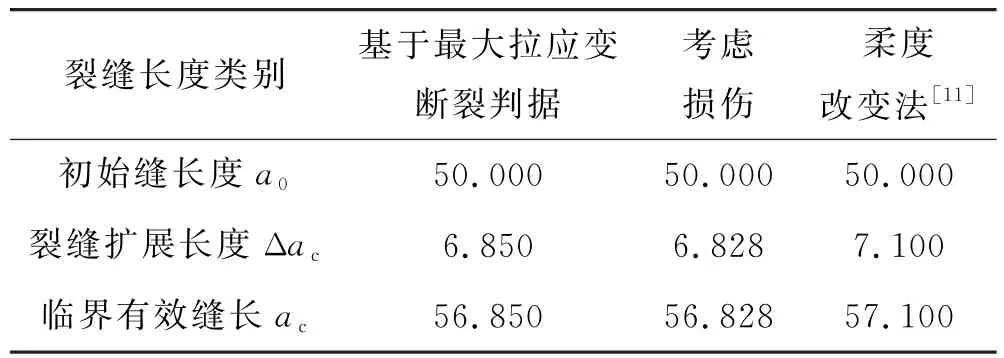
表3 裂缝长度计算结果对比(单位:mm)

根据Tada给出计算缝端应力强度因子公式[11]，

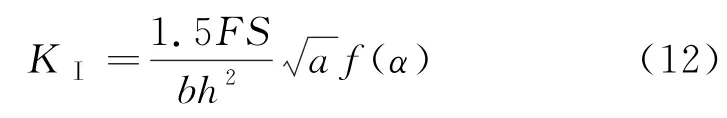
其中

式中:KⅠ为Ⅰ型裂缝应力强度因子(MPa·m1/2);F为荷载(k N);S为两支座间的跨度(m);h为试件高度(m);b为试件宽度(m);a为裂缝长度(m).

将上述计算所得有效裂缝长度代入式(12)计算，可得混凝土Ⅰ型裂缝临界失稳断裂韧度，见表4.

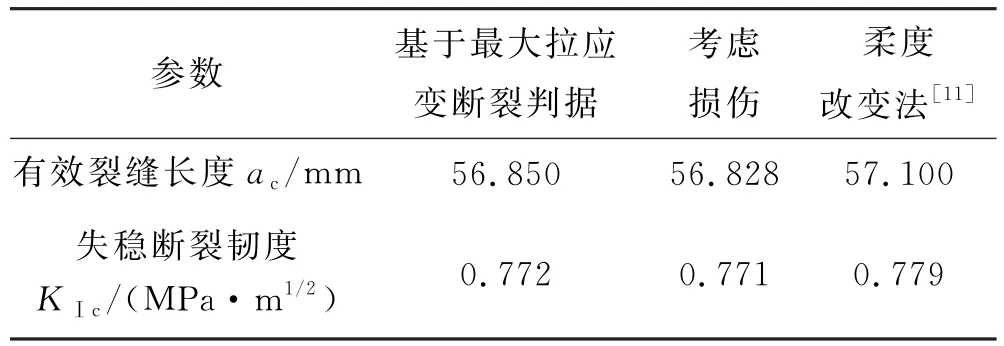
表4 失稳断裂韧度计算结果对比

根据公式(12)，将初始裂缝长度代入，计算结果为0.613 MPa·m1/2.此结果为传统计算断裂韧度方法的结果，并未考虑到在裂缝失稳扩展时，初始裂缝已经有一定长度的扩展，即断裂过程区对混凝土断裂韧度的影响.将表4计算结果与传统方法计算结果对比，可以发现，不管是文献[11]采用的柔度改变法，还是本文研究所采用的方法，最后计算所得失稳断裂韧度都比传统计算方法大，说明传统的判据偏于保守，对于工程材料的要求过于严格.而本文所采用的两种新方法计算所得断裂韧度大小介于传统计算结果和柔度改变法之间，说明混凝土宏观裂缝前端微裂缝区的断裂与损伤会使混凝土失稳断裂韧度有所降低，同时也说明本文方法的计算结果也是偏于安全的.

4 结 论

本文在文献[11]的基础上，从断裂和损伤两个不同的理论角度，对混凝土裂缝临界有效缝长的计算方法进行理论研究以及数值模拟实验计算.根据临界有效缝长的计算结果，进一步计算失稳断裂韧度，得到以下结论:

1)宏观裂缝前缘存在断裂过程区，从损伤和断裂的角度来计算临界有效缝长与文献[11]采用的基于F-δ(荷载-位移)曲线得到的临界有效缝长ac几乎一致，说明研究方法合理，为研究混凝土Ⅰ型裂缝临界有效缝长ac提供了两个新思路.

2)用不同计算方法所得ac计算失稳断裂韧度，结果表明传统计算方法偏于保守，而本文采用的方法，不仅保证了工程上使用混凝土结构的安全性问题，同时也说明宏观裂缝前缘区域微裂纹区损伤和断裂对混凝土力学性能是有影响的，即采用新方法所得ac计算断裂韧度的必要性.

3)本文Ⅰ型裂缝临界有效缝长的研究方法，可以推广到其他单一型裂缝以及各种复合型裂缝的临界有效缝长的研究中，进一步研究微裂纹区断裂和损伤对混凝土失稳断裂韧度的影响.