一类时间-空间Riesz 分数阶扩散方程的数值方法
2022-06-08 07:09邢艳元
长治学院学报 2022年2期
邢艳元
(长治学院 数学系,山西 长治 046011)
引言
分数阶微分方程能够精确刻画具有记忆与遗传特性的各类现象,常用于研究流体力学、等离子体物理、生物学、非线性电路中的流动、地震的非线性振荡、空气动力学、热力学的规则变化以及金融等领域中[1-4].分数阶微分方程是古典微分方程的推广,所以应用分数阶微分方程可以更好地刻画一些微观系统模型,并且具有广泛的理论和应用发展空间[5,6].
分数阶扩散方程常用于各种物理过程的建模当中,但只一般研究时间或空间的分数阶微分方程的各种边值问题[7-10].文章利用分数阶中心差分构造时间空间 Riesz 分数阶扩散方程的差分格式,分析其稳定性和收敛性,并提供数值算例验证理论分析的有效性.
文章考虑了带有齐次 Dirichlet 边界条件的时间空间 Riesz 分数阶扩散方程

其中,Riemann-Liouville 左、右导数分别是


1 差分格式的建立

接下来,利用 Diethlem 方法及 Riemann-Liouville 与 Caputo 导数的关系离散时间变量,并利用分数阶中心差分格式离散空间变量。令得到 Riesz 时间-空间分数阶扩散方程 (1) 的逼近格式:
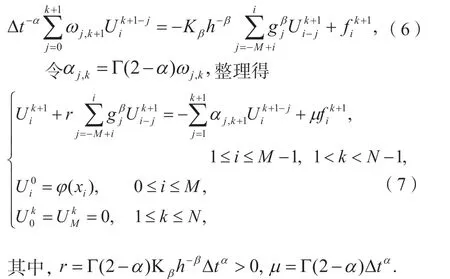
2 稳定性和收敛性

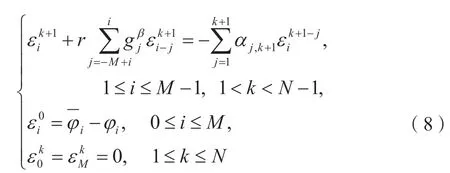
下面利用极大模技巧和数学归纳法证明稳定性.


在表1 中,通过数值实验,当 分别取1.8、1.6 和1.4 时,得到相应的收敛阶.虽然取不同的β,但收敛阶几乎是二阶精度,与理论结果一致.由表2 可见,时间收敛阶要略小于2-α.

表1 范数下的空间收敛阶

表2 范数下的时间收敛阶
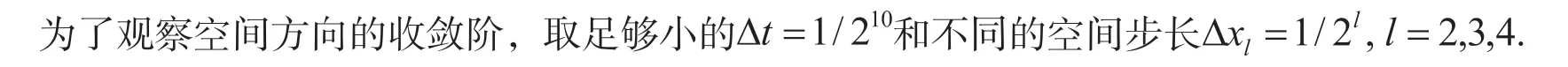
猜你喜欢
数学杂志(2022年5期)2022-12-02
新世纪智能(数学备考)(2021年5期)2021-07-28
安阳工学院学报(2020年4期)2020-09-11
数学物理学报(2020年3期)2020-07-27
数学物理学报(2019年5期)2019-11-29
中国校外教育(下旬)(2017年8期)2017-10-30
自动化学报(2016年3期)2016-08-23
应用数学与计算数学学报(2015年1期)2015-07-20
信息安全研究(2015年3期)2015-02-28

