Shapley 值的最优实现及其公理化

张 莉

（长治学院 数学系, 山西 长治 046011）

引言

合作博弈描述了参与者通过相互合作产生价值的情形.假设大联盟最终会形成，如何公平合理的分配大联盟的价值是合作博弈研究的根本问题之一.已有研究提出了各种各样的合作博弈解，其中1953 年Shapley 提出的Shapley 值[1]是最为经典的合作博弈解之一，受到研究者的广泛关注.目前，对于Shapley 值的理论研究主要集中于对Shapley 值的公理化研究[2-4]，用于说明Shapley 值的公平合理性。此外, Pérez-Castrillo从非合作的角度，给出了Shapley 值的非合作投标机制设计，证明了该机制的子博弈完美纳什均衡的均衡结果与Shapley 值是一致的[5].从优化的角度对Shapley 值进行的研究还比较缺乏.事实上，当前文献对于合作博弈解的优化实现有许多研究成果，例如1969 年Schmeidler 提出了核子[6]，核子是基于联盟抱怨，用字典序的方法在分配集中找到的最优解.类似于核子的基本思想，研究者通过定义不同的联盟抱怨，得到了广义核子[7]、SM-核子[8]、SD-预核子[9]等.

文章考虑单个参与者对于分配的抱怨，提出了一个衡量参与者抱怨的标准.基于这一标准，用字典序的方法在预分配集中得到最优解，并证明了该最优解与Shapley 值是一致的.最后，文章提出了一个新公理——个体超量相等性，该公理旨在说明每个参与者对于分配的抱怨是相等的，用有效性与个体超量相等性可以对Shapley 值进行公理化.

1 基本概念

2 主要结论

2.1 最优实现

这一小节给出Shapley 值的最优实现。具体来说，从参与者个体的角度出发，结合大联盟的形成过程，首先提出衡量单个参与者抱怨的标准，然后在预分配集中寻找使得参与者抱怨按字典序最小的预分配，该最优解与Shapley 值是一致的.

由上述定理可知，Shapley 值是预分配集中使得 按字典序最小的解.

2.2 Shapley 值的公理化

这一小节介绍一个新公理，即个体超量相等性，结合有效性，个体超量相等性可以公理化Shapley 值.

定理7 Shapley 值是唯一满足有效性和个体超量相等性的解.

证明：

（1）存在性：显然Shapley 值满足有效性.由定理5 的证明可知，Shapley 值满足个体超量相等性，且Shapley 值使得每个参与者的个体超量均为0.

有效性与个体超量相等性是逻辑独立的.

考虑均分解（简称ED）：

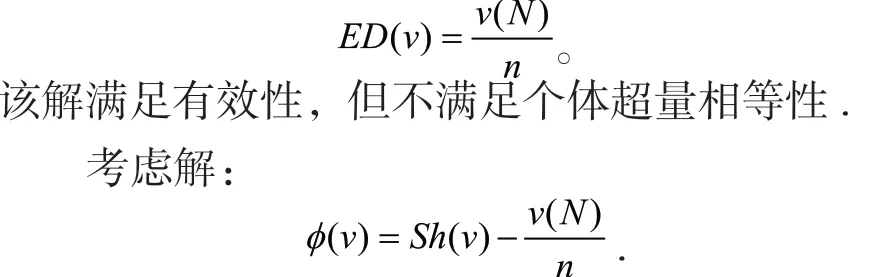
该解满足个体超量相等性，但不满足有效性.

3 结语

文章主要研究了Shapley 值的优化实现及其公理化.从参与者个体的角度定义了个体超量的概念.证明了Shapley 值是预分配集中选择使得个体超量向量按字典序最小的预分配.此外，文章给出了Shapley 值的一组公理化.对于其他合作博弈解的优化实现可进一步进行研究.