浅谈数形结合思想在听障学生学习数学解题中的应用

王 蕾

（江门市特殊教育学校，广东 江门 529000）

数学是研究数量、结构、变化、空间等概念的一门学科，是运用数量关系、逻辑关系表达客观世界的一种形式，是人类发展过程的一大重要成果，是通过对世界的观察、认识、实践演进中的智慧结晶。在从简单的数量认识到逻辑分析的过程中，人们对数学这一概念逐步有了更加清晰的认知，同时，通过不断深入的研究，运用数学这个工具解决现实问题的要求也不断提高。在这个过程中，单纯地运用观察的方法已经无法满足现实的需求，因此，数学逻辑分析应运而生。数学逻辑分析就是对数学规律、变化进行观察、比较、分析、综合、抽象、概括、判断、推理，它与单纯的数学形象思维有着本质上的区别。而人的大脑构造决定了对于形象、直观的事物易于认识和理解，而对于抽象的概念则需要通过分析、理解和判断才能被吸收和转化。

随着学生学习数学课程的深入，培养学生运用逻辑关系解决问题就摆在了教师的面前。如何有效开展对学生数学逻辑思维的培养，并以此来提升学生解题的能力，对此，我国著名数学家华罗庚给出了答案：“数缺形时少直观，形少数时难入微；数形结合百般好，隔离分家万事休。”正如华罗庚先生所言，针对数学中“数”和“形”这两个最主要的研究对象，它们之间就如同硬币的两面，有着紧密的联系，通过采取一定的方法，可以将数和形进行相互转化，相互渗透。即在数学中，“数”和“形”是抽象概念和形象概念的标志性代表，充分运用“形”的直观性来解决“数”的抽象性问题，也就是利用“数形结合”的方法解题。数形结合的基本思想，就是在解决问题的过程中，通过把“数”和“形”关联起来，根据具体情况，把图形性质问题转化为数量关系问题，或者把数量关系问题转化为图形性质问题，使复杂问题简单化、抽象问题具体化，化难为易，获得简便易行的成功方案。

而这一方法的运用，在听障学生数学教学中显得更为重要。听障学生由于语言功能缺失，导致在理解题目时存在缺陷，并且手语又不能完全表达数学术语，两方面因素的叠加，造成大脑通过手语建立语言信号系统时不全面，因此，在数学学习中，形象思维到抽象思维的转换过程出现了障碍。

在教学实践中，通过借助数形结合思想，利用图形的直观性来演示数与形之间的关系，将图形性质问题与数量关系问题灵活转换，用直观性替代抽象性，进而降低理解难度，便于听障学生有效解题。

下面就从几个方面来研究数形结合思想在教学中的应用。

1 解决集合问题

在集合运算中常常借助于数轴、维恩图（Venn diagram）来进行集合的交、并、补等的计算，从而使问题简化，运算方便快捷。［1］

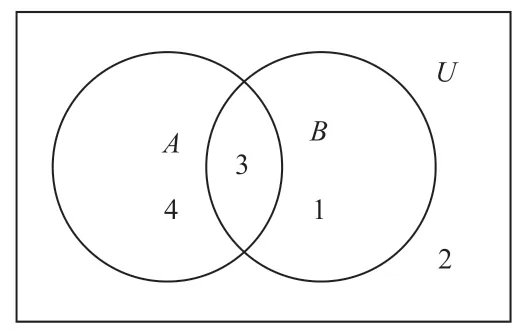
图1

2 解决函数问题

借助图像研究函数性质是一种常用的方法。函数图像的几何特征与数量特征紧密结合，体现了数形结合的特征与方法。［2］

例2.已知函数f(x)=4x2-4mx+m2-2m+2在区间[0,2]上有最小值3，求实数m的取值范围。

图2

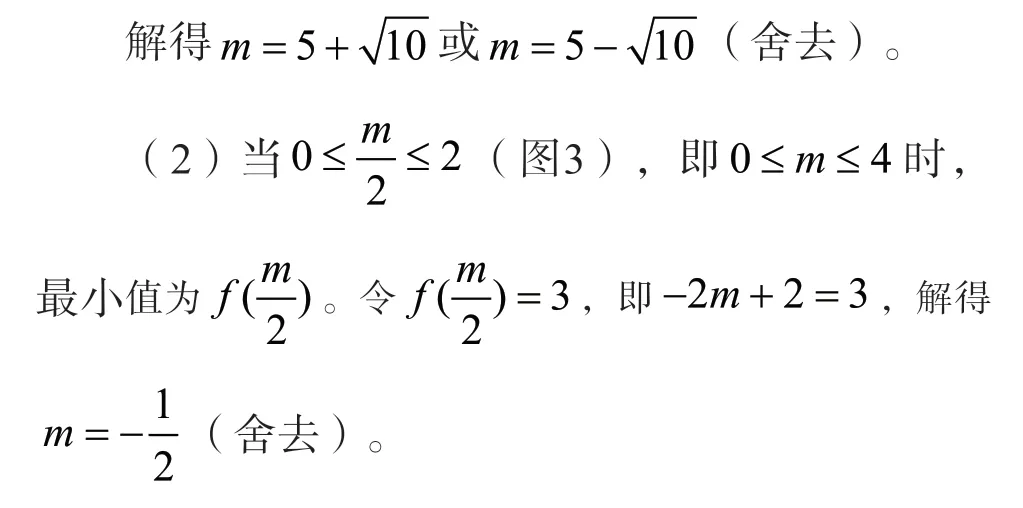
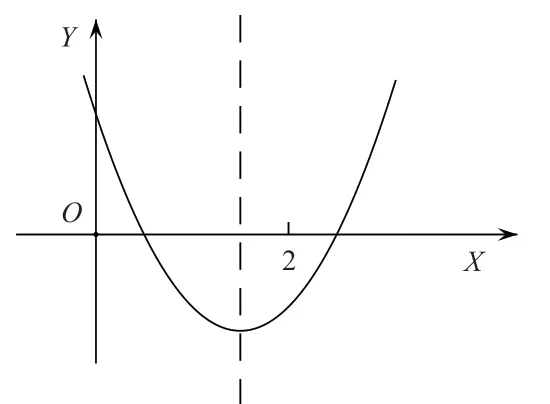
图3

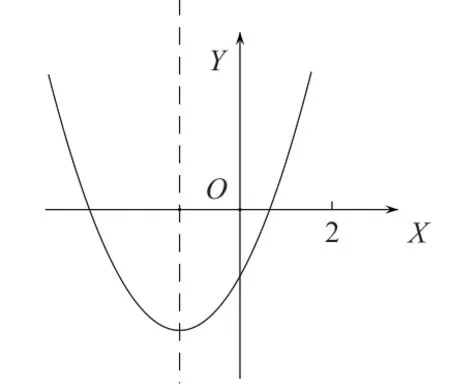
图4

如果令f(x)=4x2-4mx+m2-2m+2=0，将二次函数变成一元二次方程，利用求根公式先解出方程的两个根，再解不等式，限定根的取值范围，则计算变形非常复杂，而借助二次函数图像和性质来解题，则简单明了。

3 解决方程与不等式的问题

解决方程问题时，把方程根的问题看作两个图像的交点问题；解决不等式时，从题目条件与结论出发，联系相关函数，着重分析其几何意义，从图形上找到解题的思路。

（A）0（B）1（C）2（D）3

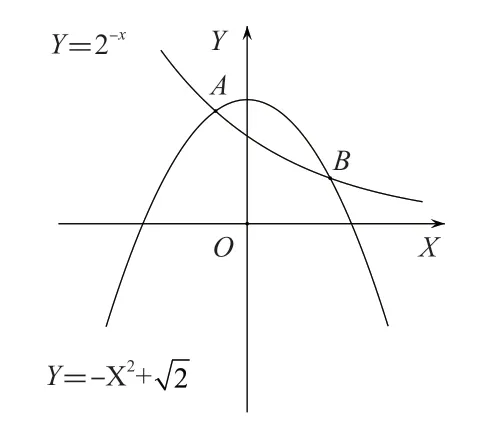
图5

这是一个超越方程，直接求解很难得出答案，利用函数图像则可轻松解题。

例4.已知a＞0，解关于x的不等式2x+a。

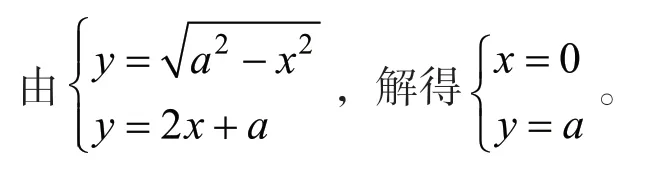
由图6知，曲线C在直线l上方部分的点的横坐标范围，就是原不等式的解集：

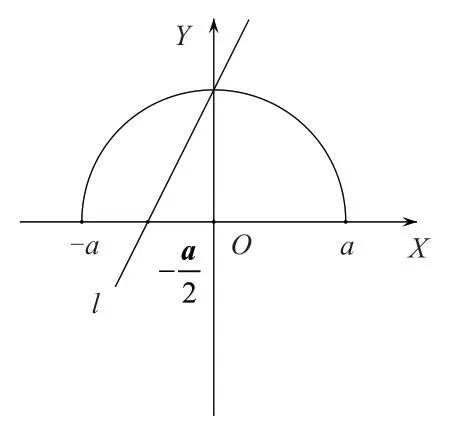
图6

4 解决三角函数问题

三角函数单调区间的确定或三角函数值大小的比较等问题，借助三角函数图像进行分析是一种有效的方法。［3］

例5.在（0，2π）内，使sinx＞cosx成立的x的取值范围为______________。

解：在（0，2π）区间上，作出y=sinx和y=cosx的图像，解出这两个图像交点的横坐标为由图7可知，sinx＞cosx时，x的取值范围为

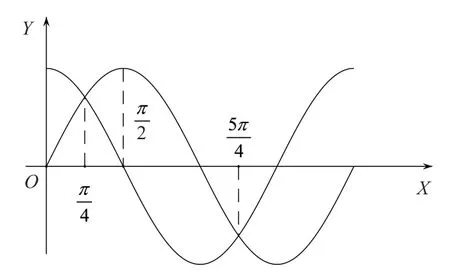
图7

5 解决数列问题

数列是一种特殊的函数，数列的通项公式以及前n项和公式可以看作是关于正整数n的函数，可以把数列问题转化为函数问题来分析，借助相应函数图像进行直观分析，常常能事半功倍。

例6.若数列｛an｝为等差数列，ap＝q，aq＝p，求ap+q。

解：假设p＜q，等差数列可以看作是关于正整数n的一次函数，所以an关于n的图像是一条直线，设ap+q＝m，因此（p，a），（q，aq），（p+q，ap+q）三个点在同一条直线上，从而三点（p，q），（q，p），（p+q，m）共线，如图8，kAB=kBC，则得m=0，即ap+q=0.

图8

6 解决解析几何问题

解析几何的基本思想就是数形结合，在解题中将数形结合的思想运用在研究点、线、曲线的性质及其相互关系中。

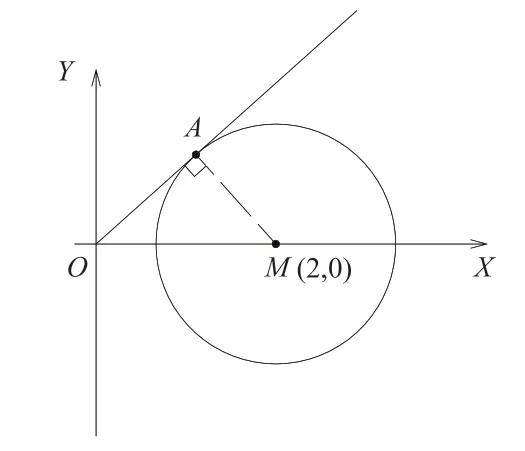
图9

7 复数问题

复数的几何意义有两种：与复平面上的点一一对应；与复平面上从原点出发的向量一一对应，因此复数问题可以从解析几何的角度来处理，借助数与形的转化解题。

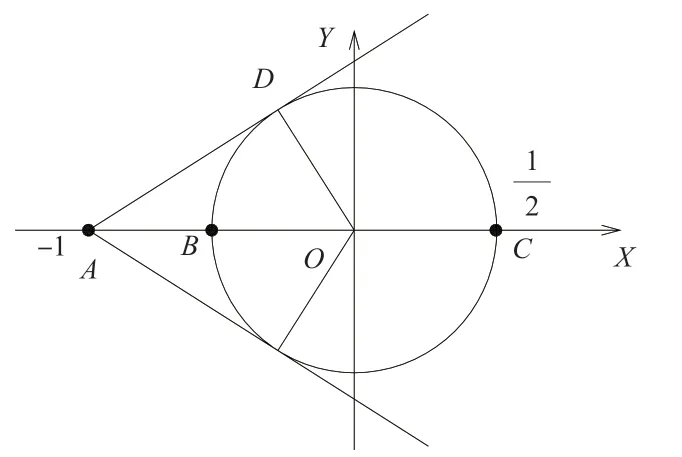
图10

本题是利用复平面上对应的图形及其几何意义来解题的，这样问题更加直观、明了。

通过数形结合的方法解题时要注意：第一，准确把握数与形转化前后的问题等价性；第二，充分运用“数”的精确性和“形”的直观性，化繁为简。

在听障学生数学学习过程中，教师要引导学生根据问题的具体情况，运用数形结合的方法，建立起抽象思维与形象思维之间的联系，通过观察和理解，找准解题的切入点，准确把握题目的核心关联性，采取抽象问题形象化的方式，进而使题目得到解决。