杆端调心球轴承主参数设计及承载能力分析
张健,袁春明,顾金芳,牛荣军
(1.中国直升机设计研究所,江西 景德镇 333001;2.上海天安轴承有限公司,上海 201108;3.河南科技大学 机电工程学院,河南 洛阳 471003)
直升机操作系统将驾驶员机械指令通过座舱操纵装置、机械线系、助力器等部件传到主桨叶,实现对直升机的姿态和航迹控制[1-3]。杆端调心球轴承作为操作系统的关键零部件,其性能和可靠性直接影响主机的性能和可靠性。操作系统用杆端调心球轴承一般在低速重载工况下摆动,失效形式与常规的疲劳失效不同,主要为强度失效[4],故其设计目标与常规轴承不同。国产杆端调心球轴承设计侧重仿制,缺乏设计分析及试验考核,与国外同类产品差距较大,亟需开展设计及试验研究。
在此以某直升机操作系统用杆端调心球轴承为研究对象,以额定静载荷为目标对其结构主参数进行优化设计,并通过仿真和试验进行验证。
1 杆端调心球轴承主参数设计
直升机操作系统一般在低速重载工况下工作,杆端调心球轴承主要承受径向载荷,同时也会承受部分偏心载荷,在此以额定静载荷为目标对其进行优化设计[5-7],初步确定轴承设计目标:1)径向额定静载荷Cr≥6.8 kN;2)轴向额定静载荷Ca≥2.1 kN。
直升机操作系统杆端调心球轴承结构如图1所示,根据操作系统使用需求,杆端双列调心球轴承外形接口尺寸:内径d为6 mm,外径(球面)D为22.5 mm,内圈宽度C为14 mm,外圈宽度B为10 mm,杆端长度L为54 mm,螺纹为M10 mm×1 mm(左旋)×37 mm。

图1 直升机操作系统杆端调心球轴承结构示意图Fig.1 Structure diagram of rod end self-aligning ball bearing for helicopter operating system
1.1 球径 Dw
根据轴承球不会碰到防尘盖,偏摆角不小于8°的设计要求,设置约束条件
Dw+2a+3h+Cb≤B,
(1)
式中:Dw为球直径;a为偏摆间隙;h为防尘盖厚度;Cb为内圈两沟道间距。
偏摆间隙可表示为
(2)
防尘盖厚度根据防尘槽深度及防尘盖形式确定,初步取0.8 mm。
考虑极限情况,Dw≈Cb,即球直径与内圈两沟道间距相同。根据上述约束条件可得Dw≤3.19 mm。参考GB/T 308.1—2013 《滚动轴承 球 第一部分:钢球》,Dw取3.175 mm。
1.2 球数 Z
球直径确定后,针对额定静载荷设计要求初步反算最小球数量。
双列调心球轴承径向额定静载荷为
(3)
轴向额定静载荷为
(4)
式中:i为球列数;K为径向额定静载荷常数,见表1;K1为轴向额定静载荷常数;Z为单列球数。

表1 不同类型轴承径向额定静载荷常数
对于杆端球轴承,K1取0.329 60,K取26.210 55,通过(3), (4)式可得不同球数双列调心球轴承额定静载荷如图2所示:1)随球数增加,径向、轴向额定静载荷线性增加;2)当球数小于13时轴承额定静载荷不能满足要求,即单列球数至少为13。

图2 双列调心球轴承额定静载荷随球数的变化曲线Fig.2 Variation curve of static load rating of double row self-aligning ball bearing with number of balls
为提高轴承承载能力,受轴承外形尺寸的限制球径无法增大,在给定空间内可考虑增加球数,球数增加到13时,径向、轴向额定静载荷分别为 6 869,2 264 N,满足要求。
1.3 其他参数
单列球数为
(5)
式中:Dpw为球组节圆直径。
由(5)式可得
(6)
载荷较大时,内圈取小沟曲率半径,即
Ri=0.52Dw,
(7)
两列球中心距为
C′=(0.875~0.900)Dw,
(8)
内圈两沟道间距为
Cb=C′+2(Ri-Dw/2)sinα,
(9)
α=arctan(C′/Dpw)。
内圈沟底直径为
d1=Dpw+2(Ri-Dw/2)cosα-2Ri,
(10)
内圈挡边直径为
d2=d1+0.3Dw,
(11)
外圈沟底直径为
D3=(d1+2Ri)/cosα-2Ri,
(12)
外圈挡边直径为
D1=D3+2Dw。
(13)
带防尘盖或密封圈双列满装向心球轴承球不与防尘盖相碰,即
Dw≤b2,
(14)
式中:θq为允许的最大内、外圈轴线倾斜角;b2为外圈沟道宽度。经计算和运动建模仿真,防尘盖为平面,偏转角为8°时球会与防尘盖相碰,防尘盖应改为外凸形,且球与防尘盖之间存在足够间隙。满足设计要求的轴承主要结构参数见表2,内圈材料为9Cr18,杆端材料为0Cr17Ni4Cu4Nb,球材料为9Cr18Mo,材料参数见表3。
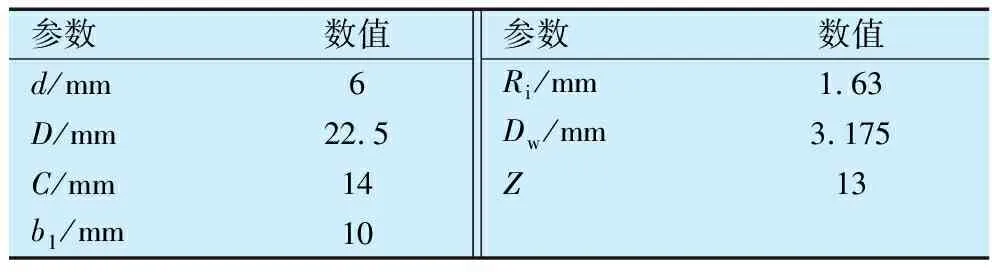
表2 杆端调心球轴承主要结构参数

表3 杆端调心球轴承材料参数
2 杆端调心球轴承静承载能力仿真分析
上述轴承参数设计初步满足额定静载荷要求,但还需分析给定额定静载荷下轴承承载能力是否满足要求。该杆端支承结构与常规轴承支承方式不同,采用有限元法分析。
基于ABAQUS建立杆端调心球轴承有限元模型,如图3所示,在杆端位置施加固定约束,在内圈内表面耦合中心施加径向载荷。

图3 杆端调心球轴承有限元模型Fig.3 Finite element model of rod end self-aligning ball bearing
由于轴承结构和受载对称,为提高计算效率,仿真时仅取一列进行分析。在6.8 kN径向额定静载荷下内圈和杆端接触应力云图如图4所示:1)单列仅7个钢球受载,在径向载荷作用方向钢球应力最大;2)内圈沟道接触应力大于外圈,故需校核内圈静承载能力。

图4 内圈和杆端接触应力云图Fig.4 Contact stress nephogram of inner ring and rod end
为进一步分析轴承是否满足要求,提取各个球位置处内圈沟道最大接触应力,如图5所示:1)最大接触应力为3 260 MPa,处于较高应力状态,但低于调心球轴承静载荷容量[6](4 600 MPa),静承载能力还有较大裕度,满足要求;2)由于杆端的柔性支承作用,承载钢球数较少,且各钢球受载不均,接触应力分布的不均匀性不利于轴承寿命的提高。

图5 不同球位置处内圈沟道最大接触应力Fig.5 Maximum contact stress of inner ring raceway at different ball positions
由于有限元仿真模型对轴承的支承方式进行了简化,且网格质量、疏密程度以及钢球与沟道的接触刚度系数等均会对计算结果产生影响,并不能完全反映轴承实际工作状态,存在局限性,还需通过试验准确评估轴承承载能力。
3 杆端调心球轴承静载荷试验
分别验证轴承径向、轴向静载荷承载能力,每组取3套轴承,参考Q AVIC 02331—2017《航空杆端双列调心球轴承通用规范》:试验前后轴承径向游隙增量不大于5 μm,轴向游隙增量不大于15 μm。
3.1 径向额定静载荷
轴承径向静载荷试验装置如图6所示,初始载荷为0,载荷升速为0.06 kN/s,直至达到6.8 kN,恒压1 min,然后以同样的速率卸载。轴承径向游隙测量结果见表4,满足要求。

1—固定连接套;2—芯轴;3—试验轴承;4—加载连接套。 图6 径向静载荷试验装置示意图Fig.6 Diagram of static radial load test device

表4 径向游隙测量结果Tab.4 Measuring results of radial clearance μm
3.2 轴向额定静载荷
轴承轴向静载荷试验装置如图7所示,初始载荷为0,载荷升速为0.02 kN/s,直至达到2.1 kN,恒压1 min,然后以同样的速率卸载。轴承轴向游隙测量结果见表5,满足要求。

1—加载连接套;2—试验轴承;3—千分表;4—芯轴;5—锁紧套;6—垫圈;7—固定连接套;8—止动套。

表5 轴向游隙测量结果Tab.5 Measuring results of axial clearance μm
4 结束语
根据直升机操作系统低速重载的使用工况,以额定静载荷为目标对杆端调心球轴承主参数进行优化设计,并通过仿真和试验验证了优化设计的正确性。但本研究仅从承载能力进行性能考核,还需进行多方面的考核试验,后续有待进一步研究。

