基于灰色BP神经网络的高速列车轴箱轴承温度预测方法

孟建军，潘彦龙，陈晓强1a,,2，祁文哲，李德仓

(1.兰州交通大学 a.机电技术研究所;b.机电工程学院，兰州 730070；2.甘肃省物流及运输装备信息化工程技术研究中心,兰州 730070)

轴承作为列车传动链条中转向架轴箱、齿轮箱、电动机重要的组成部分，在确保列车运行安全方面不可或缺[1]。列车运行中轴承异常温升严重威胁行车安全，持续的轴承高温轻则触发列车紧急制动导致经济损失，严重的可能诱发列车脱轨，造成不可挽回的后果[2]。温度可以直接反应轴承的工作状态，温度异常是轴承发生故障的重要信号。现有车载轴温监测系统可以对轴温进行实时监测，通过设定的阈值对轴温进行预警；但一旦发生报警必须立即处理，留给相关人员的处理时间少[3]。因此，研究高速列车轴承温度预测方法，对车载轴温监测数据进行分析来判断轴承的健康状态，通过轴温预测模型对轴温存在异常的轴承进行跟踪、预测，提前预警列车运行中可能存在的安全隐患，可为轴温故障处理争取更多的时间。

针对轴温的预测研究中，文献[4]通过简化热网络得到一种成本较低和速度较快的模型，比较精确地预测了电动机绕组的温度；文献[5]采用支持向量机(Support Vector Machine，SVM)的方法对太阳电池温度进行了精确的预测；文献[6]确定了影响切削温度的参数，然后采用最小二乘支持向量机(Least Squares Support Vector Machine,LS-SVM)的方法对高速切削温度预测进行了研究；文献[7]依据风电机组的运行监控数据规律，确定了影响温升的主要参数，最后采用LS-SVM的方法对齿轮和轴承温度进行了预测；文献[8]通过试验比较热网络方法建立的2种模型，将一些影响微弱的传递量略去，提出了一种简化模型；文献[9]采用非线性状态估计(Nonlinear State Estimation,NSET)的方法建立了齿轮箱温度预测模型，并对温度进行了较准确的预测；文献[10]采用NSET的方法对风力发电机后轴承温度进行了预测，用灰色关联度选择轴温的影响因素，并根据预测值与实际值的残差确定了齿轮箱的工作状态。上述研究都是基于大量故障数据进行的，列车轴温数据采集频率低且引起轴温升高的因素多，在仅知道温度的前提下判断轴承是否有故障具有灰色属性。因灰色理论具有建模样本少，精度较高的优点，利用灰色理论对轴温进行预测可以有效解决数据量少的问题。

1 数据分析处理

本文所用的数据来源于独立式温度传感器pt100测得的车载轴温数据，列车轴箱轴承数据每分钟获得1个温度值。引起轴温升高的因素较多，其中关键因素包括车辆运行速度、环境温度、载荷(轴重)、空气湿度以及润滑脂注入量等。

高速列车运行区间长，在一个区间段内有较多的站点，需要车辆频繁启停，线路不平顺也会造成列车轴承的热状态变动。通过分析列车的历史轴温数据可知，在车辆不断启停中轴承的温度随车辆运动状态的变化而波动。

1.1 轴温变化特点

列车轴温随着列车速度和运行时间的变化而不断波动，轴箱轴承温度随时间变化以及对应速度的曲线如图1所示，车辆的运动状态与轴温的波动变化可以很好地吻合：列车在单个运行区间内温度先急剧增加，然后趋于平缓，最后单调下降。温度的急剧变化多发生在列车启动加速阶段，伴随着轴承转速加快和急剧升温，在列车开始制动到停车这一阶段温度明显降低，在另外的区间段内则重复此循环。此外，由于轴箱轴承温度传感器安装于轴承座盲孔内，热量传导需要时间，因此，列车启动时轴温变化较速度变化滞后。

图1 轴箱轴承温度随车辆启停的变化曲线

1.2 数据预处理

由于采集到的原始轴温监测数据质量较差，存在缺失、重复、阶跃等问题，需要预处理。曲线拟合的方式会由于选取核函数的不同导致轴温上升趋势受到核函数的影响，而滑动平均处理(简称平滑处理)的方式则不会对原始数据变化规律造成影响，故选择平滑处理原始数据。

设选取的原始轴温数据为X=[x1,x2,…,xn]，则经过平滑处理后的数据X(0)为

(1)

式中：xi为某时刻的原始轴温。

平滑处理后的数据可重复进行相同的处理，重复处理数据的次数为迭代次数。适当的迭代次数可提高数据的平滑度，进而保证模型的精度，但迭代次数过多，数据会被处理的过于平滑而失真，不能正确反映温升规律，模型的准确度下降，不能满足建模的要求，因此，本文所取迭代次数为3。

表1 预测误差评价指标

为避免4个评价指标的结果不一致，采用局部及整体误差结合的方式对模型结果进行综合评价，其中局部误差指标选用最大绝对误差，整体误差指标选用平均绝对误差，将2种误差求和作为综合评价指标，误差越小，预测精度越高。

2 灰色BP神经网络模型

2.1 灰色模型

由于影响轴温的因素复杂，且有些影响因素采集量化较难，因此选用灰色模型对轴温进行预测，基于灰色模型的高速列车轴温预测的计算过程如下：

将平滑处理后n段时间内的轴温序列作为灰色模型的初始时间序列X(0)=[x(0)(1),x(0)(2),…,x(0)(k),…,x(0)(n)]，其中x(0)(k)≥0,k=1,2,…,n;X(1)序列为X(0)序列的一阶累加生成序列，

X(1)=[x(1)(1),x(1)(2),…,x(1)(k),…,

x(1)(n)]，

(2)

(3)

紧邻均值序列Z(1)为

Z(1)=[z(1)(2),z(1)(3),…,z(1)(k),…,

z(1)(n)]，

(4)

累加值的平均值z(1)(k)为

(5)

则灰色模型为

x(0)(k)+az(1)(k)=b，

(6)

式中：a为发展系数；b为灰色作用量。

(7)

(8)

灰色模型的解为[11]

(9)

通过累减公式得到轴温预测值序列，即

(10)

灰色模型对轴温预测的步骤如下：

1)确定模型的建模数及预测数(使用前m分钟的轴温数据对未来s分钟的数据进行预测)，为了保证预测的精度，一般s取值不宜过大，当模型的输入数据达到建模数量要求时进行预测。

2)模型的建模数及预测数确定后需对轴温原始数据进行预处理，对处理后的数据进行建模计算，得到前m分钟的模拟值及s分钟的预测值。

3)当建模窗口内进入新轴温数据时，之前的数据便可删除，不断对建模窗口内的数据进行更新补充，保证模型的输入数据最新。对轴温的变化趋势进行及时感知追踪，避免旧数据影响(不能灵敏地感知到轴温的变化)，以此提高模型的实时性及准确度。

4)将第1次模型的m个模拟值与每次求得的s个预测值进行拼接，便可得到轴温的预测序列，实现轴温的预测。

2.2 构建灰色BP神经网络模型

灰色BP神经网络模型的建模过程如下：

图2 PSO算法流程图Fig.2 Flow chart of PSO algorithm

图3 基于BP神经网络的轴温预测模型结构

4)重构模型预测值。将灰色预测值与校正的残差值相加，便可较准确地预测轴温，该预测值为灰色BP神经网络模型的预测值。

轴温的影响因素多样(图4)，而有些因素的获取困难且量化繁琐，因此设定列车的润滑程度、轴承安装情况等状态为正常水平，选用现有列车已有且易于获取的速度、运行时间、轴温、环温为灰色BP神经网络模型的输入，残差为输出进行分析计算。

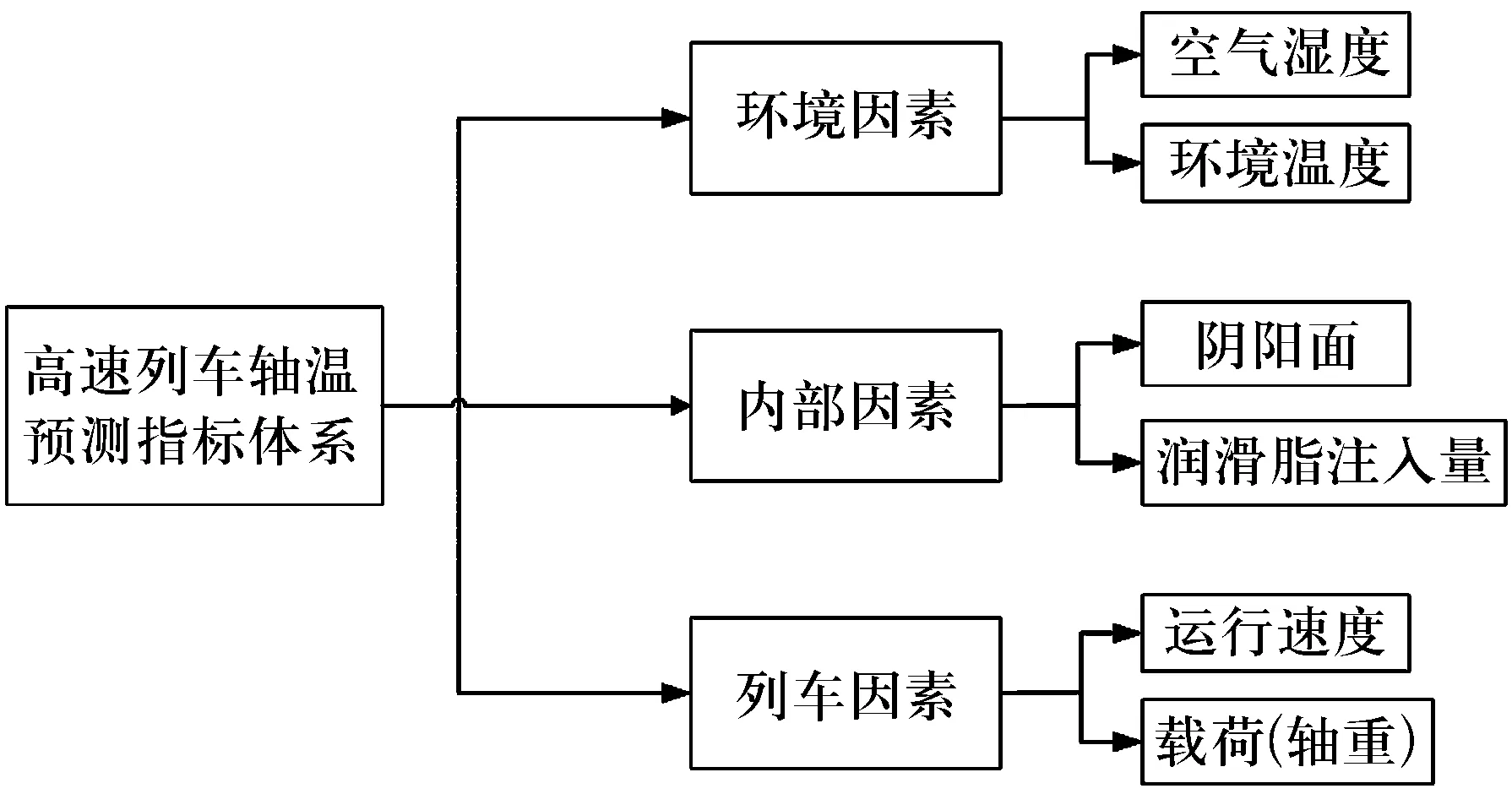
图4 轴温影响因素体系Fig.4 System of influencing factors of axle temperature

3 实例分析

为验证灰色BP神经网络模型的可行性及可靠性，以某型高速列车的履历轴温数据为基础进行预测，并将灰色BP神经网络模型与单一的BP神经网络模型或灰色模型的结果进行对比分析。灰色BP神经网络模型的输入变量为4，隐含层节点取10，输出层节点取1。隐含层选用sigmoid函数，输出层选用tansig函数，最大迭代次数取 1 000，目标精度为0.000 001，学习率为0.1。列车运行速度及轴温的部分数据见表2。

表2 列车运行速度及轴温的部分数据

3.1 灰色模型预测结果

根据轴温履历数据，按照灰色建模的步骤构建模型。首先对预处理轴温数据进行累加，然后根据生成的累加序列求得紧邻均值序列，之后求模型的白化方程式，对未知参数进行求解，推导出灰色模型轴温随时间响应公式，最后通过累减得到模型的预测值，需要计算残差对模型进行可靠性评估。用最小二乘法求得模型参数值为：发展系数a=-0.040，灰色作用量b=13.217。灰色模型预测的部分结果见表3。

表3 灰色模型预测的部分结果

3.2 灰色BP神经网络模型预测结果

图5 基于灰色BP神经网络的轴温预测结果

以评价模型误差的指标对模型进行分析，发现灰色模型、BP神经网络模型、灰色BP神经网络模型的综合评价指标分别为9.80，3.82，2.53，说明灰色BP神经网络模型预测精度较高。

表4 轴箱轴承温度预测误差

3.3 试验验证

为进一步验证模型的普适性，选取某高速列车轴箱轴承故障的一段温度数据进行分析，该轴承故障为内圈磨损(图6)，原因为在高速运行时滚子受到的摩擦加剧，打破油膜润滑平衡导致润滑失效，引起其与内圈接触，使内圈磨损。

图6 轴箱轴承故障情况Fig.6 Fault condition of axle box bearing

如图7所示，运用灰色BP神经网络模型对轴承故障情况下的某时段轴温进行预测，在样本点67 min处对轴温进行未来5 min的预测，得出温度在73 min处超过轴箱轴承的温度预警值80 ℃，而在实际样本中，温度在74 min处超过预警值。在轴箱轴承温度触发预警时，车辆采取限速措施，并在前方站点进行停车检查。

图7 轴温异常情况下预测结果

4 结束语

以轴箱轴承为例，依据灰色模型所需数据量少，BP神经网络非线性映射能力较强的特点，采用灰色BP神经网络模型对轴温进行预测。由于列车热轴故障发生次数相对较少，先选取轴承正常运行数据进行分析，之后选取一段故障时的轴温数据进行试验分析，发现灰色BP神经网络模型在轴温正常及异常情况下均可较准确地预测轴温。通过对异常温升测点在未来短时间内的温度预测，争取到更多的处理时间，为行车策略调整提供依据。