基于永磁传动的滚动轴承-转子系统振动特性研究
牟红刚,薛桥,丁莉,宗剑,韩伟
(江苏航空职业技术学院,江苏 镇江 212134)
0 引言
永磁传动是近些年发展起来的新型传动技术,典型代表产品是永磁联轴器(又称永磁耦合器或磁力耦合器)。根据工作过程中永磁联轴器的主动转子与从动转子有无转速差,可分为同步永磁联轴器(Synchronous Permanent Magnet Coupling,SPMC)和异步永磁联轴器(Asynchronous Permanent Magnet Coupling,APMC),其中SPMC更受关注,在工作过程中具有无温升、无发热现象和传动效率高的特点,可安装于机械传动系统的驱动轴与负载轴之间,实现轴间转速和转矩的传递。SPMC依靠永磁体的磁力进行非接触传动,能够起到一定的隔振降噪作用;相对于传统刚性或挠性联轴器而言,SPMC允许较大的对中误差(甚至毫米级),因此大大节省了安装对中时间,另外还具有过载“打滑保护”等特点,目前在钢铁、水泥、电力等行业的机械传动系统已有较多应用。
对机械转子系统开展动力学特性研究的成果较多:文献[1]将挠性联轴器耦合的多转子系统在耦合处分开,利用总体耦合矩阵建立多转子系统的振动微分方程,求得多转子系统的固有频率、临界转速等;文献[2]建立了无心车床空心主轴系统的三维动力学模型,对比分析了不同轴承位置时的固有频率及相应的振动特性,并对空心主轴结构进行了优化;文献[3]采用拉格朗日法建立了磨机偏心转子系统动力学方程,分析了柔性联轴器对系统振动特性的影响并计算了系统受到扰动时的响应,随着柔性联轴器阻尼的增加,系统的振动减小;文献[4]基于整体传递矩阵法和成对轴承分析理论,建立了电主轴-轴承-外壳系统动力学模型,并提出电主轴整机临界转速、电主轴轴端动态刚度的计算方法,结果表明电主轴外壳悬臂端是薄弱环节,增强外壳强度能明显提升电主轴的临界转速与动态刚度;文献[5]对锥齿轮传动转子-轴承系统的纵弯扭耦合振动特性展开研究,主要讨论了外载荷对轴承特性的影响,研究发现转速较低时,传递扭矩对轴承的刚度和阻尼系数影响较大;文献[6]建立了两跨三支承轴系动力学有限元模型,研究转子不平衡激励对轴系振动特性的影响,结果表明该转子轴系跨内加重振动以单转子不平衡振动特性为主,转子间振动相互影响较大;文献[7]建立了永磁同步电主轴有限元模型,研究不平衡磁拉力对电主轴动态性能的影响,发现气隙偏心引起的不平衡磁拉力导致电主轴振动加剧;文献[8]分析了多联组配角接触球轴承的预紧载荷和刚度,并与SKF和NSK公司轴承进行了比较,误差在3%以内;文献[9]采用弹性流体动力润滑理论推导出圆柱滚子轴承径向刚度的计算公式,实例计算表明该计算方法精度较高;文献[10]对角接触球轴承作为径向支承和永磁悬浮轴承作为轴向辅助支承的电动机转子-轴承系统的动力学特性进行研究,结果表明增大转子支承刚度可以改善转子的动态特性;文献[11]对飞刀铣削高速气浮电主轴转子进行了动态特性研究,建立了一个五自由度转子动力学铣削模型,结果表明转子质量偏心引起的离心力和周期性的切削力共同影响主轴转子的振动特性。
相比于传统刚性或挠性联轴器,SPMC应用于机械传动轴系必将对轴系的振动特性产生一定的影响,然而,该方面的研究成果却鲜有报道。以永磁传动在某离心泵转子系统的应用为例研究SPMC对离心泵转子系统动力学特性的影响规律,便于SPMC在其他机械传动轴系(尤其是高速机械传动轴系)的推广应用,以期解决机械传动系统常见的振动和噪声大,甚至共振等问题。
1 离心泵转子系统结构
采用永磁传动的离心泵转子系统如图1所示,电动机额定功率55 kW、电压380 V、额定输出转速3 000 r/min。该离心泵转子系统主要由电动机转子轴、SPMC、泵转子轴、滚动轴承及叶轮组成。电动机转子轴的轴径处安装有角接触球轴承Ⅰ和Ⅱ;泵转子轴左侧轴径处背靠背安装角接触球轴承Ⅲ和Ⅳ,泵转子轴右侧轴径处安装有圆柱滚子轴承Ⅴ,4套角接触球轴承型号(7314B)相同,预紧力为570 N;SPMC为同步筒式结构,主要由主动转子和从动转子组成,其主动转子与电动机轴连接,从动转子与离心泵轴连接,主动转子与从动转子之间依靠气隙内磁力线实现非接触传动。

1—轴承Ⅰ;2—电动机转子轴;3—轴承Ⅱ;4—SPMC主动转子;5—SPMC从动转子;6—轴承Ⅲ;7—轴承Ⅳ;8—泵转子轴;9—轴承Ⅴ;10—叶轮。
2 转子系统的支承刚度计算
一般情况下,滚动轴承在径向力及轴向力联合作用下,内外圈将产生径向、轴向的相对位移和相对倾角,通常将内外圈产生单位位移量所需的外载荷定义为轴承刚度。因此,该传动系统中的滚动轴承将作为弹性支承考虑,轴承对轴的弹性支承如图2所示。文献[10]给出了修正的角接触球轴承的径向刚度Kr计算公式,即
(1)
式中:ξ为修正系数(轻预载荷取1.8;中预载荷取1.9;重预载荷取2.0);Z为球数;Dw为球直径;α为工作接触角;Fa0为球轴承的轴向预紧力。

1—轴;2—弹性支承。 图2 轴承对轴的弹性支承示意图Fig.2 Diagram of elastic support of bearing to shaft
同理,圆柱滚子轴承作为弹性支承考虑,其径向刚度Kr由油膜刚度Kf和接触刚度Kn串联而成,径向刚度的计算公式为[9]
(2)
(3)
(4)
C=0.28β0.54(μ0ni)0.7r0.43(R1+r)0.7·
(w1.13u0.7+u1.13w0.7)E′-0.03Z0.13l0.13,
(5)
γ=r/(R1+r),
w=1-γ,
u=1+γ,
E′=E/(1-ν2),
式中:r为圆柱滚子半径;R1和R2分别为内、外滚道半径;E′为综合弹性模量;E为材料弹性模量;ν为泊松比;Fr为径向力;l为圆柱滚子有效接触长度;ni为内滚道转速;μ0为润滑油黏度;β为黏压系数。
考虑电动机转子轴两轴径处的角接触球轴承Ⅰ和Ⅱ在工作过程中受相同的初始预紧力,计算时两轴承的径向刚度相同;但离心泵在工作过程中叶轮会受到较大的工作轴向力,泵转子轴背靠背安装的角接触球轴承Ⅲ和Ⅳ受轴向预紧力有所不同,轴承Ⅲ相对“放松”,而轴承Ⅳ相对“压紧”,因此,需考虑该工作轴向力对轴承径向刚度的影响。根据(1),(2)式可得4套角接触球轴承和圆柱滚子轴承的径向刚度分别为Kr1=Kr2=281 N/μm,Kr3=281 N/μm,Kr4=356 N/μm,Kr5=645 N/μm。
3 永磁传动转子系统的模态分析
建立离心泵滚动轴承-转子系统的三维有限元模型如图3所示,各滚动轴承均作为弹性支承考虑。该轴系中SPMC为同步筒式结构,其主动转子与从动转子的永磁体为偶数块,N-S磁极交替排列布置,相互之间依靠磁力作用进行非机械接触式转矩传递。理论上,SPMC在工作过程中主动转子与从动转子之间的轴向力为零,径向合力也为零(因主动转子与从动转子之间磁拉力的切向分力用于传递扭矩,径向分力的合力为零)。因此,模态分析时可将SPMC的主动转子与从动转子作“隔离”处理,即将电动机转子轴与SPMC主动转子、泵转子轴与SPMC从动转子作为多部件进行分析。

图3 离心泵滚动轴承-转子系统模型Fig.3 Model of centrifugal pump rolling bearing-rotor system
3.1 电动机转子轴
对电动机转子轴进行模态分析,其前6阶固有频率和临界转速见表1,电动机转子轴的第1,2阶模态固有频率为0(转速0),代表电动机转子轴作刚体自由振动;电动机转子轴第3阶与第4阶、第5阶与第6阶模态固有频率相同,代表电动机转子轴在正交方向上的振动。

表1 电动机转子轴的固有频率和临界转速
提取电动机转子轴的第1,2,3,5阶模态振型进行分析,如图4所示:图4a主要表现为电动机转子轴的径向膨胀振动;图4b主要表现为电动机转子轴的轴向自由振动;图4c主要表现为电动机转子轴安装SPMC主动转子的径向弯曲振型;图4d主要表现为电动机转子中间部位的径向弯曲振型。由图4可知,电动机转子轴振动变形最严重部位在SPMC主动转子,要改善电动机转子轴的振动特性,需要提高电动机输出轴轴径处的径向支承刚度。

图4 电动机转子轴模态振型Fig.4 Modal shapes of motor rotor shaft
3.2 泵转子轴
对离心泵转子轴进行模态分析,泵转子轴的前6阶固有频率和临界转速见表2:第1阶模态代表泵转子轴作刚体自由振动;第2阶模态代表泵转子轴作刚体轴向振动;第3,4阶模态固有频率相同,代表泵转子轴在正交方向上的振动;同理,第5,6阶模态固有频率相同,代表泵转子轴在正交方向上的振动。

表2 泵转子轴的固有频率和临界转速
提取泵转子轴的第1,2,3,5阶模态振型进行分析,如图5所示:图5a、图5b为刚性自由振型,其中,图5a主要表现为泵转子轴的径向膨胀振动,图5b主要表现为泵转子轴的轴向自由振动;图5c、图5d为泵转子轴的径向弯曲振型,其中,图5c实际为泵转子轴的一阶弯曲临界转速振型,主要表现为泵转子轴上叶轮部位的径向弯曲振型,图5d为泵转子轴的第5阶径向弯曲振型,主要表现为泵转子轴安装SPMC从动转子的径向弯曲振型。由图5c、图5d可知,泵转子轴振动变形最严重部位在泵叶轮处和SPMC的从动转子处,故要改善泵转子轴的振动特性,需要提高泵转子轴左右两轴径处的径向支承刚度。

图5 泵转子轴模态振型Fig.5 Modal shapes of pump rotor shaft
4 永磁传动转子系统的谐响应分析
4.1 系统不平衡磁拉力的计算
对永磁传动的离心泵转子系统进行谐响应分析,首先要确定激振源。该离心泵系统的激振源主要有:1)电动机定子与转子之间的不平衡磁拉力;2)SPMC两转子之间的不平衡磁拉力;3)叶轮的不平衡力。本文不考虑电动机的不平衡磁拉力,主要研究后两者对转子系统振动特性的影响。其中,SPMC不平衡磁拉力的产生原因是电动机转子轴与泵转子轴之间存在轴间安装误差,引起SPMC主动转子与从动转子之间存在安装误差,尤其是两转子之间存在的径向安装误差Δx,如图6所示;而叶轮的不平衡力主要由叶轮在高速旋转状态下因其制造误差、装配误差等产生的离心力所致。

图6 SPMC结构示意图Fig.6 Structure diagram of SPMC
为了研究SPMC主动转子和从动转子因径向安装误差而产生的不平衡磁拉力对泵转子系统振动特性的影响,需要计算主动转子和从动转子在不同径向安装误差Δx下的SPMC磁密分布及不平衡磁拉力,仿真计算时所用的SPMC相关技术参数见表3。

表3 SPMC相关技术参数
通过电磁仿真软件进行磁路计算,计算SPMC主动转子和从动转子的径向安装误差Δx分别为0.5,1.5 mm时的SPMC磁密分布,如图7所示,由于径向安装误差的增大,导致偏心侧磁密值变大,两者的最大磁密值相差约17.6 mT。进一步计算SPMC主动转子和从动转子在不同径向安装误差Δx时产生的不平衡磁拉力F。通过仿真计算可得不同径向安装误差Δx对应的不平衡磁拉力如图8所示,随着径向安装误差的增大,两转子的不平衡磁拉力也变大,且径向安装误差与不平衡磁拉力基本呈线性关系。
4.2 谐响应分析系统
建立电动机转子轴和泵转子轴的谐响应分析模型如图9所示,将SPMC的不平衡磁拉力作为周期性激振力作用于电动机转子轴端和泵转子轴端(图9中F和F′分别为作用力与反作用力),图9b中Fc为叶轮的不平衡力。同时取电动机转子右轴承位置M1、离心泵转子左轴承位置M2及右轴承位置M3为振动监测点。

图7 不同径向安装误差的SPMC磁密分布图

图8 SPMC不平衡磁拉力散点图Fig.8 Scatter diagram of unbalanced magnetic tension of SPMC

图9 永磁传动转子系统谐响应分析模型
4.2.1 单一激振源对转子系统振动特性的影响
研究SPMC在Δx分别为0.1,0.5,1.0,1.5 mm时不平衡磁拉力F对电动机转子轴和泵转子轴振动特性的影响。以SPMC的不平衡磁拉力为单一激振源,分别对电动机转子轴和泵转子轴施加激励,进行振动特性分析,求解图9中M1和M2的径向(x向)振动速度频谱图。
M1和M2的振动速度频谱图分别如图10、图11所示,随着SPMC主动转子和从动转子的径向安装误差Δx的增大,M1和M2的振动速度增大;在工作频率(50 Hz)附近时,当Δx为1.5 mm,M1的径向(x向)振动速度为1.08 mm/s,M2的径向(x向)振动速度为0.51 mm/s。由此可知,SPMC的径向安装对同轴传动轴系的振动影响并不敏感,SPMC允许轴系间存在较大的径向安装误差,这也表明了永磁传动具有良好的减振特性。

图10 电动机右轴承位置M1的频谱图Fig.10 Spectrum diagram of right bearing position M1 of motor

图11 离心泵左轴承位置M2的频谱图
4.2.2 多激振源对转子系统振动特性的影响
为研究多激振源对泵转子系统振动特性的影响,除考虑SPMC的不平衡磁拉力F外,还需考虑叶轮的不平衡力Fc对转子系统振动特性的影响。假定SPMC主动转子和从动转子的径向安装误差Δx为1.0 mm,此时SPMC产生的不平衡磁拉力F为160 N,分3种工况(Fc分别为50,100,150 N)对离心泵转子轴进行振动特性分析。
在不平衡磁拉力F和叶轮的不平衡力Fc共同激励作用下,M2和M3的径向(x向)振动速度频谱如图12所示:在多激振源的共同作用下,随着叶轮不平衡力Fc的增大,M2和M3的径向振动速度增大,特别是在一阶临界转速4 728 r/min(对应频率78.8 Hz)附近尤为显著,此处的振动速度幅值最大,而离心泵的额定工作转速远远低于一阶临界转速,尚未发生共振。因此,为了改善泵转子轴的振动特性,需要尽量减小叶轮旋转时的不平衡力Fc,即减小叶轮的制造、安装误差。当泵在额定转速3 000 r/min附近工作时,叶轮不平衡力Fc为150 N时,M2的径向振动速度为0.32 mm/s,M3的径向振动速度为0.13 mm/s,此值远远小于许用振动值,所以采用永磁传动的离心泵系统可以安全平稳工作。
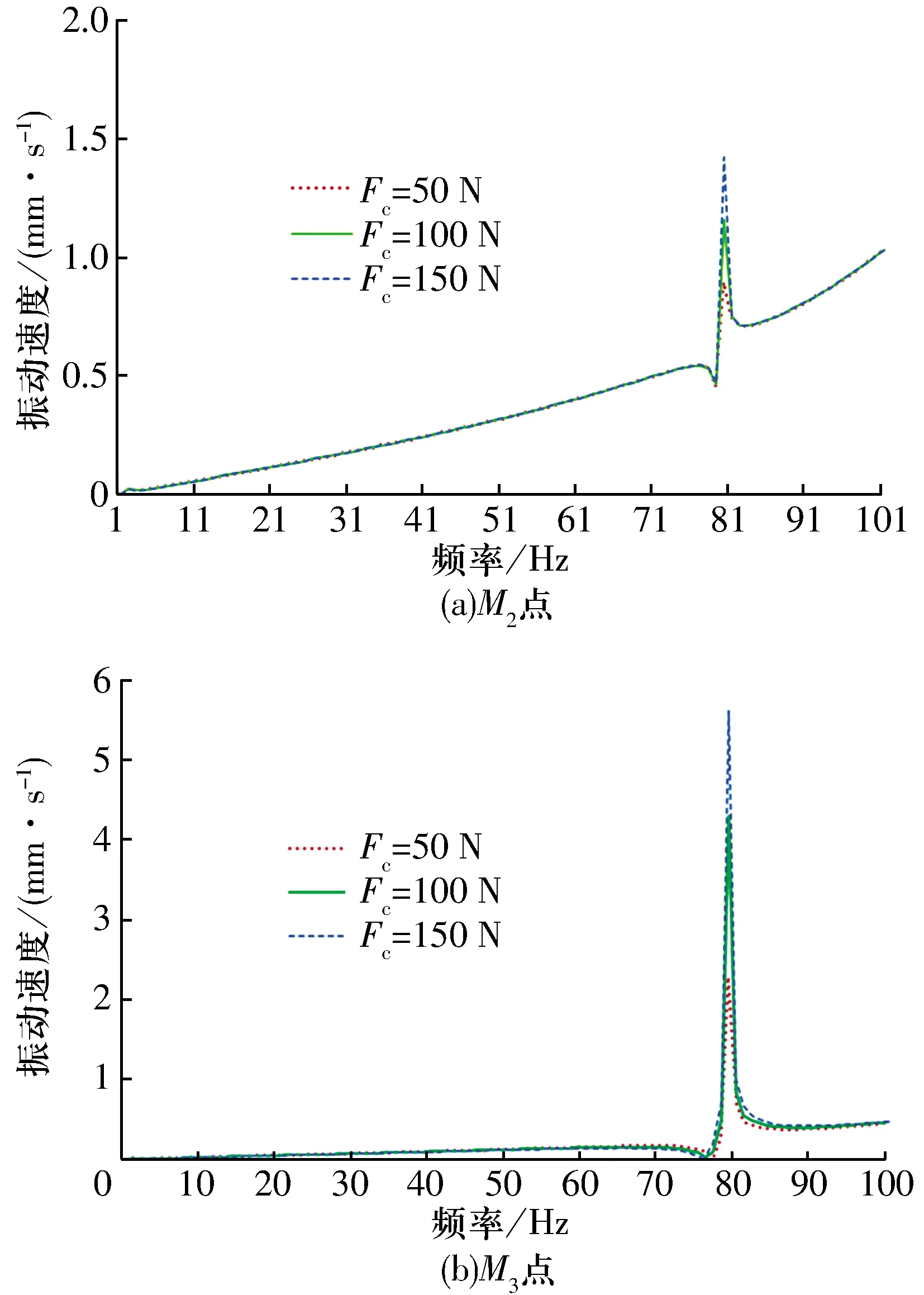
图12 多激振源作用下离心泵左、右轴承位置M2,M3的频谱图
5 结论
对采用SPMC的某离心泵转子系统进行振动特性分析,得到以下结论:
1)该离心泵的实际工作转速避开了电动机转子轴和泵转子轴的各阶临界转速,转子轴系不存在共振风险。
2)SPMC的径向安装误差对同轴传动轴系的振动影响不敏感,当轴间径向安装误差为1.5 mm时,电动机右轴承位置M1的径向振动速度为1.08 mm/s,离心泵左轴承位置M2的径向振动速度为0.51 mm/s,表明采用永磁传动的轴系具有良好的振动特性。
3)在SPMC不平衡磁拉力和叶轮不平衡力的共同激励作用下,离心泵左轴承位置M2和右轴承位置M3在一阶临界转速(4 728 r/min)附近径向振动速度幅值较大,但在工作转速(3 000 r/min)附近,两测点的振动速度均较小,完全能够满足使用要求。

