隧道管环端面平整偏差自动评估技术研究

张红升， 宋伟浩

(中交疏浚技术装备国家工程研究中心有限公司， 上海 200082)

0 引言

利用盾构进行隧道建设，常采用多环连接的通用型楔形管片作为隧道最内层支护结构。同一管环由多块轴向长度不同的预制管片拼接而成[1-2]，管环中管片的位置变动超限会降低隧道建设质量并造成安全隐患，而管环端面平整度作为事关盾构施工安全和管环成型质量的指标，受到了更多的重视。若管环端面平整偏差过大，容易造成相邻环因局部受力过大导致管片破裂。因此，实现管环端面平整偏差的自动测量，可为人工补偿平整度偏差提供数据支撑，有效避免因不平整造成的管片破裂，提高平整偏差人工补偿效率，提升盾构掘进施工安全性和管环成型质量。

现有工程规范中未见管环端面平整偏差相关内容，与之相近的技术指标为管片错台。受到推进油缸纠偏顶力不均、壁后注浆压力过大、本环管片拼装状态等多种因素影响，导致管环容易发生管片相对位移，其中相邻管片沿接缝发生的位移称为管片错台[3-5]。管片错台可分衬砌环内错台和衬砌环间错台[6-7]，分别用于描述同环内相邻管片纵缝错动距离和相邻成型管环环缝错动距离，并可通过激光点云技术进行测量[8-10]。管片错台是衡量管环成型质量的指标，但管环错台指标不足以描述管环端面整体平整程度，依照业界施工需求和实践经验，可将掘进过程中与撑靴相接触的管环端面的各测量点相对理想管环平面的偏离距离称为管环端面平整偏差(简称平整偏差)，作为平整程度评判指标和人工补偿平整偏差的参考数据。

现阶段，业界对管环端面平整度的研究工作有限，当前工程中主要通过人工测量管环平整偏差[11]，未见相关自动测量技术应用案例。测量人员利用全站仪测量当前环端面的多个测量点坐标后，选取两两距离最远的3个测量点作为基准点并计算校准平面方程，进而计算各测量点至该平面的距离得到对应距离偏差值。该人工测量方法存在以下弊端： 1)人工选定的3点任意性较大，无法保证基于该3点计算的目标平面为最佳平面； 2)盾构施工场景空间狭小，人工操作全站仪进行测量难度较大且测量效率较低，难以满足盾构施工对测量时效性的要求。相较于人工测量，本文所研究测量技术可实现对管环端面平整度的自动、实时评估。

本文通过研究盾构物理结构和掘进施工工艺，构建测量原理的几何模型，在原理上明确仅需推进油缸行程即可实现对管环端面平整偏差的自动测量，并进一步设计算法和硬件解决方案，实现对管环平整偏差的实时、自动测量。研究结果以期为平整偏差的人工补偿提供数据支撑，减轻测量人员劳动负担，提高测量效率。

1 测量原理

实现管环端面平整度自动测量的要点在于管环端面多点坐标的自动测量，解算偏差距离的关键在于如何合理选取校准平面。结合盾构施工推进油缸和管片端面相支撑的工程实际，可借助推进油缸行程传感器测量管环端面相对盾构的距离数据，结合油缸在安装平面的弧度，即可实现自动采集测量点在盾构坐标系下的位置数据。盾构与管环相对位置关系如图1所示。记推进油缸活塞杆轴线与管环端面交点为测量点，与推进油缸装配圆面交点为基点，基点与测量点距离记作l。

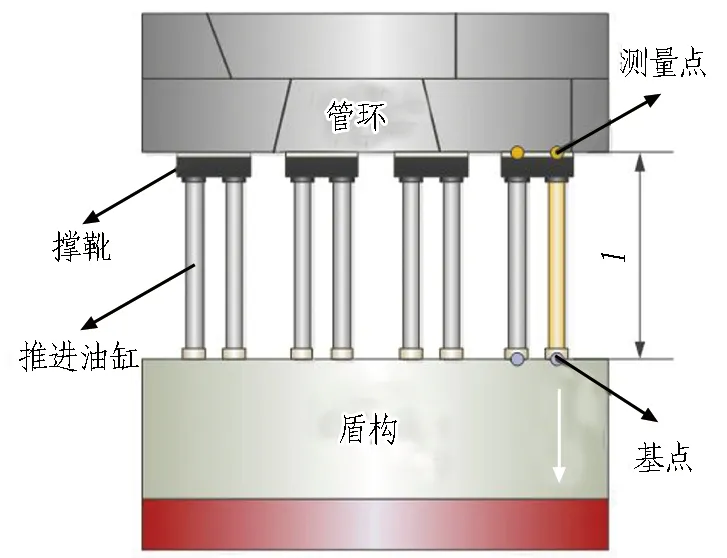
图1 盾构与管环相对位置关系图

斜截圆筒模型及其展开示意见图2。如图2(a)所示，推进油缸装配平面为一垂直于后盾体轴线的圆面，各推进油缸沿安装面圆周分布，且油缸轴线垂直于该圆面。由于一环完整管环存在一定楔形量，故理想情况下拼装完整的管环端面为一空间椭圆环。如图2(b)所示，理想情况下可将管环端面椭圆、油缸装配圆面、油缸轴线组成的空间结构视为一斜截圆筒。在三维空间内可计算各测量点坐标和校准平面，但需要事先精准测量基点空间坐标，且解算过程较繁复，需要多方软硬件系统支持。为降低系统实现难度和减少计算资源占用，可依照下述方法将计算过程转换至二维空间[12]： 将如图2(b)所示的斜截圆筒沿任意一条母线展开至二维平面(如图2(c)所示)，各基点所在圆周对应二维平面一条直线，测量点所在管环端面椭圆对应二维平面一条曲线，推进油缸行程即为两线相应位置的间距。

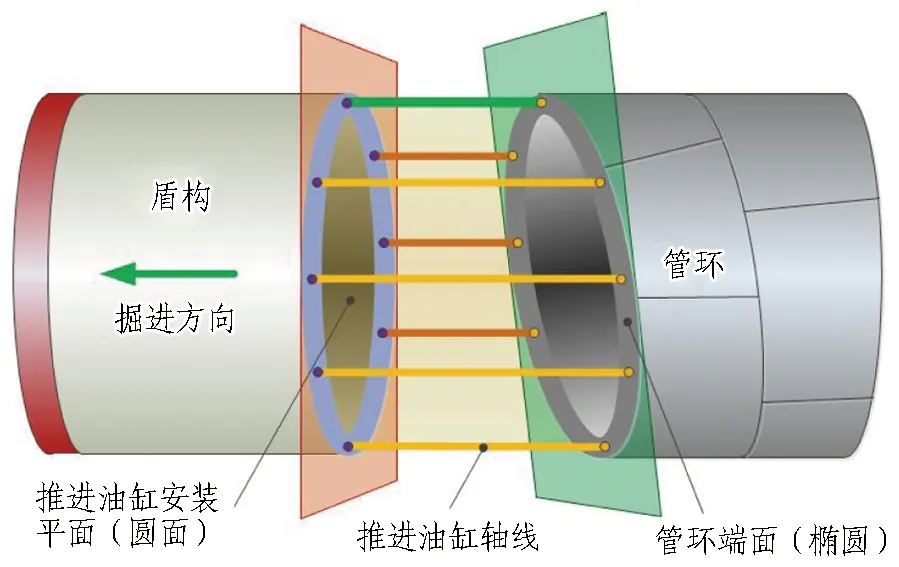
(a) 关键部位空间形状与相对位置示意图

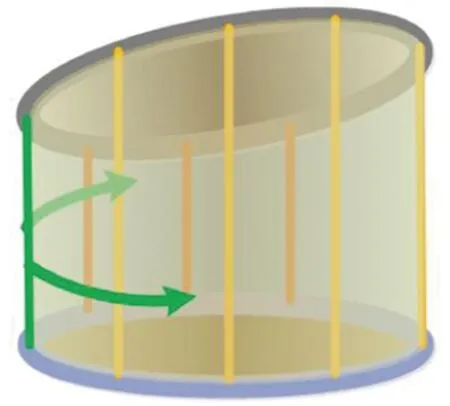
按上述方法可将三维空间内点面关系转换为二维平面内点线关系，由此只需获取测量点所在曲线方程的数学模型即可通过数据拟合方式获取校准曲线(对应三维空间校准平面)，进一步在平面直角坐标系内计算得到管环端面平整偏差。

1.1 数学模型

盾构推进油缸装配圆面、推进油缸和管片椭圆面抽象为斜截圆筒如图3(a)所示，以斜截圆筒底面圆一点为原点O，以过O点的底面圆直径为X轴，以过O点且指向椭圆面的母线作为Z轴，利用右手法则确定Y轴方向。过底面圆O1沿圆筒轴线与上部椭圆环最近点作平行于圆O1的空间圆O2，圆O1与O2的距离为h1，圆O2与上部椭圆环最远点的距离为h2，斜截圆筒的对称面与X轴负方向夹角为α，圆O1圆周任意一点A与X轴负方向夹角为θ。

为便于叙述，将用于数学模型推导的部分放大后如图3(b)所示。任一测量点G和对应基点A的间距li可等效为线段AG长度，其数值可按照式(1)计算：

|AG|=h1+|DG|。

(1)

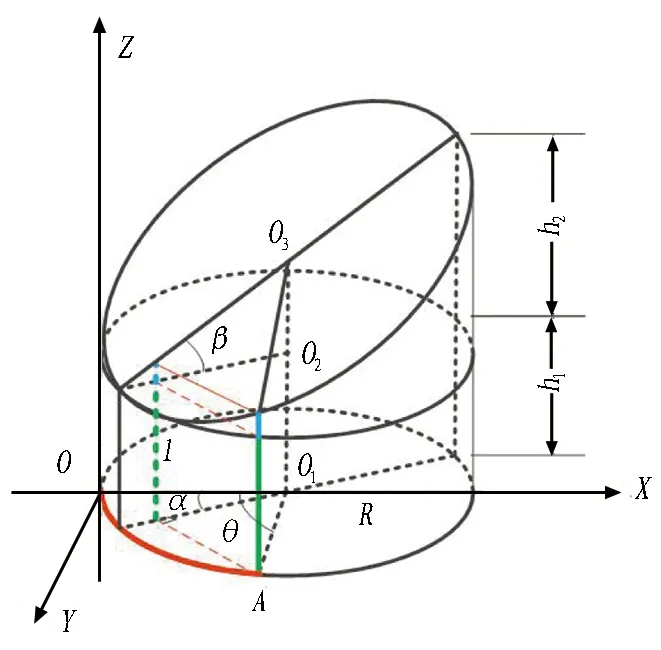
(a) 几何模型整体示意图

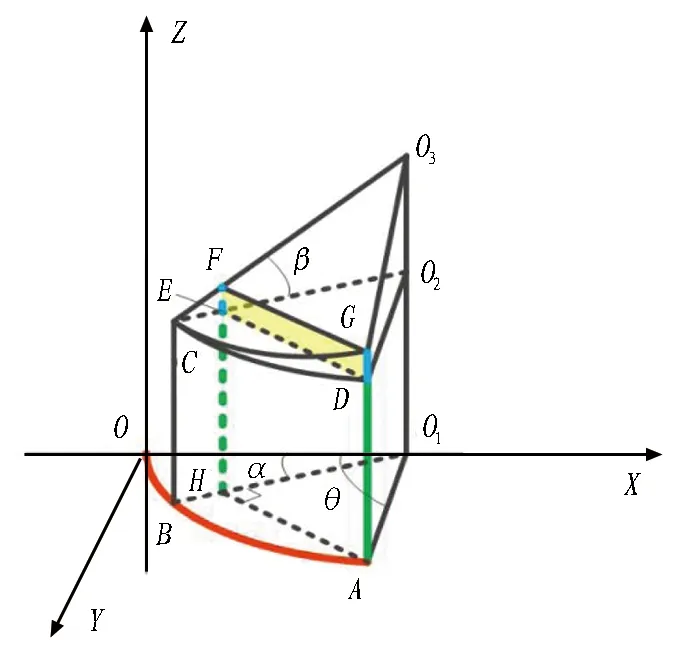
(b) 模型解算示意图

由于平面BO1O3E与斜截圆筒的圆端面和椭圆端面都垂直，又因平面AHFG、平面BO1O3E以及圆O2所在平面两两相互垂直，故四边形AHFG为矩形，进一步可知四边形DEFG也为矩形，则|EF|=|DG|。线段EF长度可在△CEF内按照式(2)求解：

|EF|=|CE|·tanβ。

(2)

在矩形BCEH中|CE|=|BH|，而线段BH长度可由式(3)解算：

|BH|=|O1B|-|O1H|=R-R·cos(θ-α)。

(3)

式(2)—(3)中，正切值tanβ可由h2和各基点所在圆O1的半径R按式(4)计算得出：

(4)

综合式(1)—(4)，可得油缸行程表达式：

(5)

进一步化简可得油缸装配角度与管环端面间距在平面直角坐标系θOl内的数学模型：

li=a·cos(θ+b)+c。

(6)

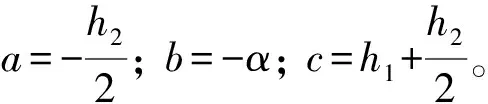
由式(6)可知，斜切圆筒母线长度与对应圆周角呈三角函数关系。式中参数b所含的相位信息由管环最短管片F块与盾构0π位置的相对位置关系决定。综上，在理论上证明了仅通过油缸行程传感器数据即可测量管环端面平整偏差。

1.2 算法实现

各油缸在装配圆面的对应圆心角(简称油缸安装角度)依照如图4所示获得： 从盾尾看向盾首方向，记盾构最上方为0π位置，角度顺时针递增，则第i根油缸相对0π位置圆心角为定值θi，相应的经过补偿修正后活塞杆行程(基点与测量点间距)记为li。参照所推导θ-l数学模型，在展开的二维空间直角坐标系θOl中，各测量点的位置信息可由(θi,li)完整表述。

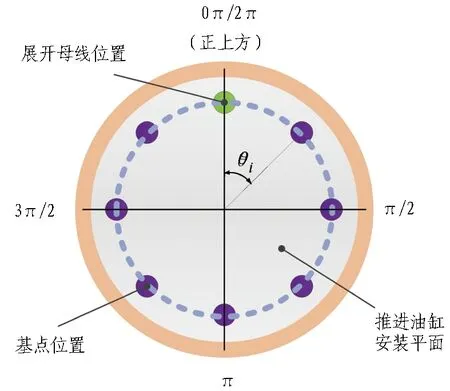
图4 圆心角描述方式示意图

获取n组油缸长度实际测量数据y1,y2,…,yn后，可对应匹配得到n个测量点坐标(θi,yi)。式(6)可转化为式(7)所述形式，通过数据拟合即可得到此时管环端面椭圆环对应的二维曲线，称为基准曲线l0。

l0(θ)=li=c1·cosθ+c2·sinθ+c3。

(7)

式中:c1=a·cosb;c2=-a·sinb;c3=c。

为便于利用最小二乘法求解上述系数[13-15]，构造矩阵如下：

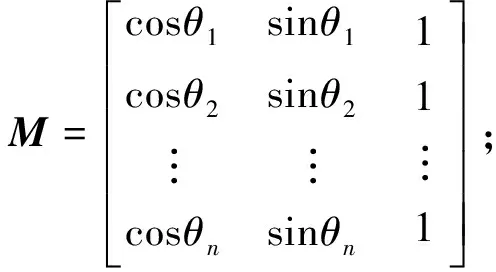
将残差平方和作为优化目标函数：

(8)

当残差平方和E最小时，当前数据下最优的系数矩阵X0可由式(9)计算得出，对应的曲线为基准曲线l0。

X0=(MTM)-1MTY。

(9)

如图5所示，实际测得测量点坐标值为(θi,yi)，通过数据拟合出三角函数各系数后得出基准曲线l0(图5中粗实曲线)。由于施工要求仅可使用传力垫片填补短缺距离进行平整偏差补偿，故需保证各测点对应偏差为正值，以便于人工进行后续偏差补偿。需筛选出位于基准曲线l0下方且距离基准曲线l0最远的测量点，将曲线l0向下(盾构掘进方向)平移至其经过最远距离点，此时所得曲线即为校准曲线l1(图5中虚曲线)。计算各测点沿纵轴至校准曲线l1的距离，即得出三维空间内各测量点相对校准平面的偏差值。设基点与基准曲线l0沿l轴距离用Δdi表示，各基点与校准曲线l1沿l轴距离用di表示。校准曲线l1具体由如下策略获取：

1)通过Δdi=yi-l0(θi)计算油缸行程实际间距与拟合间距的差值，并筛选出最小值△dmin及对应的测量点P′。

2)向l轴负方向平移曲线l0至其经过点P′，此时得到的曲线为校准曲线l1,l1(θi)=l0(θi)+Δdmin。

3)利用式di=yi-l1(θi)计算所有测量点沿l轴方向至校准曲线的距离，即可得出管片前沿横断面各测量点对应的距离偏差值di。

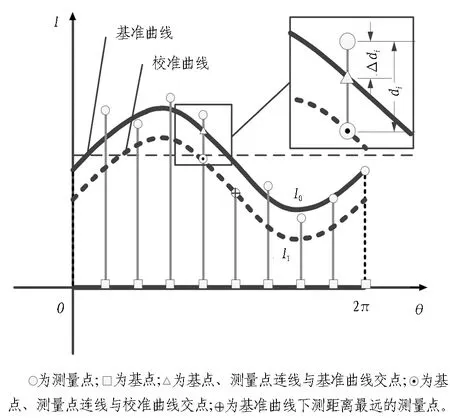
图5 校准曲线l1计算方法示意图

2 系统实现

管环平整偏差自动测量系统基于盾构推进系统硬件实现，包括盾构推进油缸行程传感器、可编程逻辑控制器(PLC)、工控机。推进油缸行程传感器用于测量盾构盾尾基点和对应管环端面测量点的间距；PLC用于将传感器模拟量信号转换为数字信号，并传输至工控机；工控机用于处理多组间距数据，计算出各测量点与校准平面距离偏差。管环端面平整偏差测量流程如图6所示。

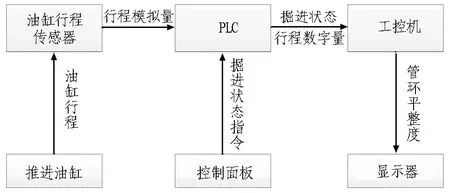
图6 管环端面平整偏差测量流程图

该系统按下述步骤实现管环平整偏差自动测量：

1)推进油缸行程传感器实时测量掘进状态中各活塞杆伸出长度。

2)PLC读取位移模拟量并进行数字量转换和补偿修正得到测量点与基点距离，同时监测盾构司机通过控制面板发出的盾构掘进状态指令。

3)上位机从配置文件读取各推进油缸装配角度，同时从PLC读取测量点与基点间距数据，对应匹配组成多组弧度-行程数据，实时计算管环端面平整偏差数据并展示在显示器，供工作人员评估管环平整偏差状态。

4)上位机实时从PLC获取盾构掘进状态信息，在盾构由掘进状态切换至拼装状态瞬间，显示器显示本环测量结束信息和掘进结束时刻管环端面距离偏差数据，为作业人员补偿管环端面偏差距离作参考。

3 工程实践

在南京某隧道工程项目中，对该系统进行了应用测试。工程中隧道采用2 m楔形管环，其内径为13 300 mm，外径为14 500 mm，每环管环由10块管片组成，其中F块轴向长度最短为1 976 mm，B4块轴向长度最长为2 024 mm。该工程采用刀盘直径为15.03 m的泥水平衡盾构作为施工装备，该型盾构共配备28组(56根)推进油缸，各组推进油缸间隔角度为2π/28，且装配了内置/外置式油缸行程传感器用于测量油缸行程。盾构掘进过程中受到负载不均衡等因素影响，实时采集的推进油缸行程数据波动较大，对平整偏差测量准确性产生较大不良影响。对实时采集数据进行滤波处理，提高所测数据的平稳性，但实时解算的平整度数据仅能用作端面平整程度参考。应在掘进结束且油缸撑靴尚未脱离管环时进行数据采集，计算管环端面平整偏差并据此进行平整度补偿。

在保证各组传感器正常工作的情况下，取某环掘进结束的油缸行程测量数据进行验证。由于盾尾下部经常性积水，难以正常安装使用行程传感器，未能采集第13、14、15组油缸行程数据，故共采集25组角度-油缸行程数据，数据处理结果见图7。对上述数据进行拟合获得基准曲线l0(θ)=li=-66.56·cosθ+61.29·sinθ+2 852.07，对应图中蓝色实线。在基准曲线下方且距离基准曲线最远的测量点为第25组油缸对应测量点，偏差为-5.53 mm，将基准曲线平移后得到校准曲线l0(θ)=li=-66.56·cosθ+61.29·sinθ+2 846.54，对应图中橙色虚线。

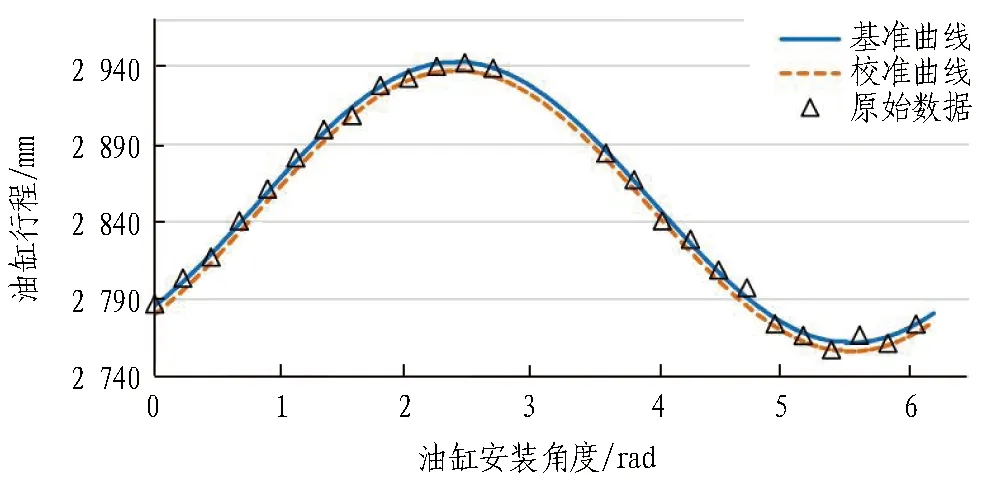
图7 校准函数曲线

计算各测量点沿纵轴至校准曲线的距离即为所求平整偏差，相应平整偏差曲线见图8(a)中橙色圆点标识曲线。鉴于人工测量技术与自动测量技术虽技术路线存在差异但具备相同的技术思路，即通过处理采集的管环端面测量点坐标获取校准平面/曲线，进一步计算各测量点至校准平面/曲线偏差距离。由于未有施工规范对平整偏差测量做出规范要求，为评估测量方法有效性，将人工测量结果作为参照组。由人工利用跟踪仪测量对应测量点空间坐标并选取3点适当测量点计算校准平面，进一步计算各点至该平面距离即为人工测量的平整度偏差数据，相应曲线见图8(a)中蓝色菱形点标识曲线。将系统自动测量结果和人工测量结果作差对比，相应曲线见图8(b)。由图可知，所述系统计算得到的平整偏差和人工测量结果变化趋势相同，但由于选取校准平面/曲线的标准不同，所得平整偏差也存在差异，但差值大小都在±4 mm以内。

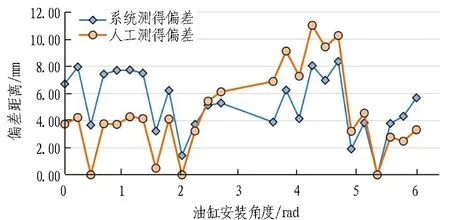
(a) 偏差距离与油缸角度曲线

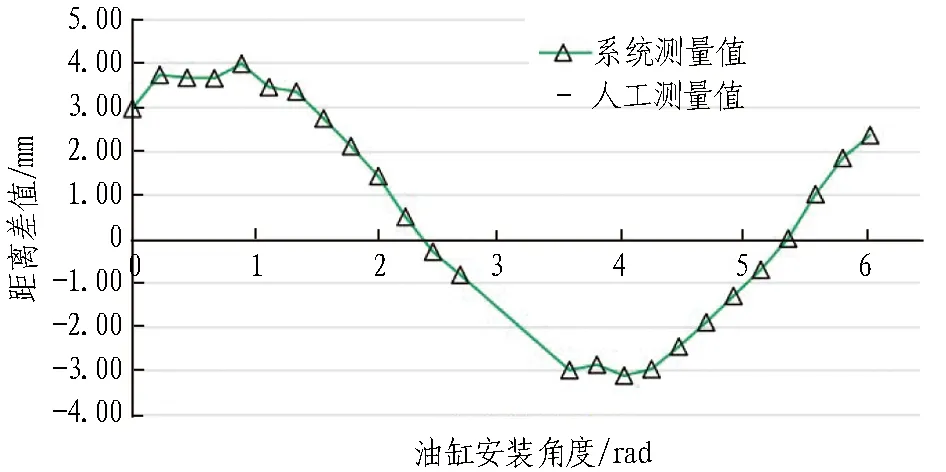
(b) 自动测量与人工测量结果差值曲线

在实际项目中应用和验证了所研究方法，若需要测量管环端面所有撑靴位置平整偏差，则要求所有油缸组均配备行程传感器;若传感器损坏或测量失效，则无法有效估计对应位置的平整偏差。另外，在掘进过程中需要对传感器测量数据进行滤波处理，减小测量数据波动对平整偏差评估准确性的影响。对比系统和人工测量结果可知： 系统测量结果相较于人工测量结果偏差更均衡且最终结果唯一。两者偏差曲线近似三角函数，说明2种不同的校准平面选取方法最终解得的平面存在一定夹角，但测量结果偏差较小，均满足工程应用需求。

4 结论与讨论

经过实际应用和数据验证可知： 根据管环平整偏差的测量需求、盾构结构及施工特点，推导了测量数学模型，证明可在二维空间内便捷计算评估平整偏差。根据盾构结构特点设计并实际应用了利用油缸行程数据评估管环平整偏差的技术方案，数据结果表明所述系统测量结果有效、技术方案可行。该技术的实施应用实现了管环端面平整偏差的自动实时测量。

为获取更优的测量结果，下一步研究可从以下方面改进： 研究采用更优的滤波技术获取更贴近真实的距离数据，弱化盾构掘进过程中传感器测量数据波动的不良影响。由于盾构施工工况恶劣，传感器易发生损坏或测量失效，故可以进一步研究传感器状态评估和异常数据识别与滤除技术，减少因个别传感器测量异常对整体评估结果造成不良影响。