伞衣优化设计对群伞系统气动特性的影响分析

董海波，隋 蓉，黄明星

(北京空间机电研究所， 北京 100094)

随着深空探测逐渐成为全球载人航天活动的重要发展方向，主要航天国家均积极开展新型可重复使用的多用途载人飞船研制或研究论证[1-2]。当航天器完成任务返回地球时，为了确保航天器能够安全可靠的着陆于地球表面，航天器回收系统起着至关重要的作用。降落伞仍是应用较为广泛的航天器气动减速装置，其回收载荷质量从数吨级的载人航天器、返回式卫星，直至60吨级的航天飞机助推器等，例如我国的“神舟号”飞船降落伞[3]以及美国波音公司的星际线飞船的降落伞系统[4]。针对大载重航天器伞系减速系统的需求，在降落伞减速回收技术方面，可以采用两种方案实现：一是通过增大降落伞的阻力面积提高减速能力；二是选择合适大小的单伞，通过增加降落伞的数量来提高减速能力，相对于采用单一降落伞的回收系统，采用多伞组合方式的设计方案统称为群伞技术[5]。以7吨级别的回收载荷为例，如果仍采用单伞系统减速方案，则需求的降落伞面积约2 500 m2，而如此大面积单具降落伞的加工工艺、特纺材料性能、折叠包装都会带来难以突破和解决的问题，导致单伞系统方案和可靠性均不能满足减速需求。采用群伞系统减速方案时，若由三具主伞组成群伞系统，单伞面积需求约900 m2；若由四具主伞组成群伞系统，单伞面积需求约720 m2。这一规模的单具主伞，可充分继承已有成熟降落伞的设计方案，其结构布局、加工工艺和折叠包装方法均比较成熟且继承性较好，单伞数量可根据系统方案、回收载荷质量、单伞面积以及安装空间进行优化组合。

航天器减速着陆系统主要工作在飞行过程的最后一个阶段，在非常有限的工作行程内，需要将拥有巨大的动能和位能的航天器安全着陆停留在星球表面，位置、速度和姿态均要发生很大的变化，特别是对于载人飞船而言，其工作的成败直接关系到整个飞行任务的成败[6]。美国在20世纪60年代的阿波罗(Apollo)载人飞船和21世纪初的猎户座(Orion)载人飞船[7-8]中针对群伞技术做了大量的研究工作。美国多用途乘员飞行器(multi-purpose crew vehicle，MPCV)是基于猎户座乘员飞行器所研制，飞船执行完既定任务时在正常状态下返回地球的工作步骤如图1所示。

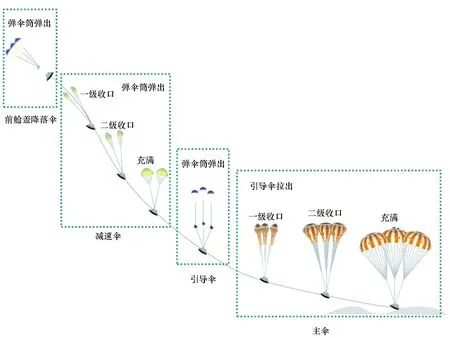
图1 多用途乘员飞船减速着陆过程示意[9]Fig.1 MPCV descent and landing sequence[9]

MPCV的回收过程主要分为四个阶段[10]：①前端防热罩伞工作(forward bay cover parachutes，FBCPs)，MPCV通过自身携带的静压高度控制器进行开伞高度的实时判别，当满足开伞高度后首先弹射3具前端防热罩伞，降落伞充气展开并提供阻力；②减速伞工作，前端防热罩与MPCV完成分离后，瞬间弹射2具减速伞，在高速外界气流的作用下，减速伞采用2级收口方式完成充气减速过程；③引导伞工作，减速伞分离后，仍然采用弹射方式拉出3具引导伞，每一具引导伞分别对应一具主伞；④主伞工作，3具主伞采用单独拉出的方式开伞，整个充气过程同样采用2级收口方式进行充气控制。在整个减速着陆过程中，如果降落伞在充气时无法正常工作，出现降落伞失效故障，肯定会导致载人飞船的非正常减速现象，严重的可导致整个回收任务的失败。历史上曾发生多次因主伞失效造成的回收故障，甚至完全失败[11-12]。因此，减速着陆系统最重要的特点之一是必须具有高可靠性，应尽量采用冗余技术等提高可靠性的措施，在执行载人航天活动的整个任务过程中，减速着陆系统的可靠工作为航天员提供了生命保障。

以美国猎户座飞船为例，其群伞技术研究以三代空投试验为主线，第一代空投试验的目标是初步的系统性功能原理验证，试验对象为各个阶段的单伞及简单的群伞[13]；第二代空投试验的目标是进行降落伞结构的优化改进，并通过试验与仿真相结合的方式提高仿真能力建设[14]；第三代空投试验的重点在于对系统失效模式的探索验证[15]。但是，猎户座群伞技术的研发成本也是一个不可忽略的问题，猎户座群伞设计分为三个阶段，研究过程集设计、仿真、空投试验、风洞试验、摄影测量、工艺改进等于一体，经历了从第一代设计中的单一降落伞功能性验证到第三代设计中对于群伞多故障模式的验证，研究过程层层递进。由于进行全尺寸空投试验成本高、周期长，其研究过程历时数十年才取得目前的研究成果，这是其他国家无法承受的研究成本。为了降低成本并缩短研发周期，在群伞技术研究中可结合相关技术开展群伞的缩比等效设计，采用缩比空投试验的方式在短周期内进行大批量试验，与同等缩比的风洞试验进行了对比[16-17]。另外，随着计算机硬件条件和理论方法的不断发展，针对流体流动的数值模拟以及求解相应Navier-Stokes方程(NS方程)的算法研究现已成为国内外备受关注的热点和前沿课题，采用计算流体力学(computational fluid dynamics，CFD)方法对群伞气动性能的模拟也取得了很好的研究成果[18-22]。由于航天器在返回着陆的过程中经历了多种流速状态，其下降过程中的非定常流动现象相当复杂，导致全流速条件下的数值仿真工作难度巨大，因此本文针对亚声速条件下减速着陆系统的工作状态进行研究，分析不同群伞设计构型下整个系统的气动特性，以仿真结果为基础进行降落伞结构优化设计工作，以此来提高仿真技术在降落伞设计过程中的使用程度，缩短研发周期并降低试验成本，为群伞技术在大载重回收任务的推广应用提供理论保证。

1 数值方法

近年来，飞行器非定常气动力计算方法主要有两种：一种是势流理论方法，如片条理论法、偶极子格网法、非定常涡格法等[23]；第二种是CFD方法[24]。基于势流理论方法的计算网格生成简单，计算效率高，但计算精度不够理想，特别是对于非定常效应很强的问题。虽然发展出了许多改进的势流理论方法，但是这些方法的计算精度还是非常有限，并且大多存在待定参数，因此应用起来非常复杂。此外，这些方法大多数只停留在二维问题的研究。

CFD方法是一种通用性较好的非定常气动力计算方法，并且能达到较高的精度。在连续流区，气体假定为连续介质，基于此假设可建立相应流体力学控制方程，并可采用多种数值格式对方程进行离散求解，目前常见的CFD方法有基于Euler方程和NS方程的方法，后者又可分为雷诺平均N-S方程(Reynolds averaged Navier-Stokes, RANS)模拟、大涡模拟(large eddy simulation, LES)和直接数值模拟(direct numerical simulation, DNS)。CFD计算不仅能给出升力、阻力特性，还能给出流场结构随时间变化的细节，如边界层复杂流动、流场涡、激波运动等。而在稀薄流区，气体密度减小，分子平均自由程逐渐变大，当分子平均自由程可与飞行器特征长度相比拟时，气体间断粒子效应凸显，飞行器周围流场出现稀薄气体效应，传统连续介质假设不再成立，而需要采取微观分子模型或者稀薄气体动力学的方法[25]进行流场求解。

1.1 流动控制方程

群伞系统处于稳降阶段时，当地的海拔高度往往在5 km以下，其下降速度也小于20 m/s[26]，因此降落伞的工作环境属于不可压缩范围，针对不可压缩流动，可以采用压力基求解方法进行N-S方程的求解。对于不可压缩流动，连续性方程和动量方程分别为：

∇·u=0

(1)

(2)

式中，ρ为流体密度，u为速度矢量，u、v和w分别为三个方向的速度分量，P为压力。

方程(2)中黏性应力与流体变形率成正比，其表达式为：

(3)

式中，μ为动力黏性系数，λ为第二黏性系数。

对于存在能量交换、化学反应、组分输运以及湍流影响等复杂流动问题时，控制方程的通用形式为：

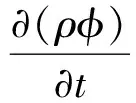
(4)

其中，φ表示通用变量，Γ为广义扩散系数，S为广义源项。式中各项依次为顺态项、对流项、扩散项和源项。所有的控制方程均可经过适当处理，将方程中因变量、瞬时项、对流项与扩散项写成标准形式，然后将其余各项集中于方程右端定义为源项，从而简化为通用微分方程。

1.2 求解方法

针对不可压缩流动的N-S方程求解，本文采用压力耦合方程组的半隐式方法(semi-implicit method for pressure-linked equations, SIMPLE)算法[27]对控制方程进行求解。SIMPLE算法是一种半隐式求解方法，属于压力修正法范畴，其基本思想为：通过初始给定的压力场求解离散形式的动量方程，获得拟速度场。因为初始给定的压力场可能是不准确的，求解得到的拟速度场一般不能满足连续性方程，需要对压力场进行数值修正。修正过程中遵循的规则为：与修正后的压力场所对应的速度场能够满足该迭代步的连续性方程。以此为基准，将动量方程所规定的压力与速度代入连续性方程，获得压力修正方程，求解压力修正方程得到压力修正值。采用修正后的压力场，获得新的速度场。对数值解进行收敛判别，若不收敛，用修正后的压力值作为初始值，开始下一次的迭代计算。如此反复，直到获得收敛的数值解。

2 计算结果

在群伞系统处于稳降状态下，受外界气流的影响，单伞之间可能会发生碰撞现象，这种故障状态在猎户座群载人飞船进行空投试验时也多次发生[28]。为避免该故障模式，研究人员采用多种方法对环帆伞开展分析研究，其中包括数值模拟方法。本文在不同学者研究经验的基础上，针对群伞系统中广泛使用的环帆伞设计构型，通过对不同设计方案在亚声速条件下开展气动特性数值模拟，结合数据对比进行分析研究，不断优化群伞中单伞的设计构型，以此来提高群伞系统在稳降阶段的稳定性。

2.1 单伞仿真

2.1.1 仿真模型

环帆伞伞型采用球台加圆顶锥的结构形式，如图2所示。伞衣上部采用环缝形结构，与环缝伞结构类似，下部采用环帆形结构，即上、下环片结合处采用非等长设计，上环片的底边比下环片上边缘长，形成月牙状。在伞衣充气初期，气流可以从月牙缝进入，有助于快速开伞。伞衣充气后，气流从月牙缝向下排出，可增加伞衣阻力。根据降落伞设计经验，本文所采用的降落伞环帆总数为16，其中环型数目为6，帆型数目为10，伞衣总数目为80。

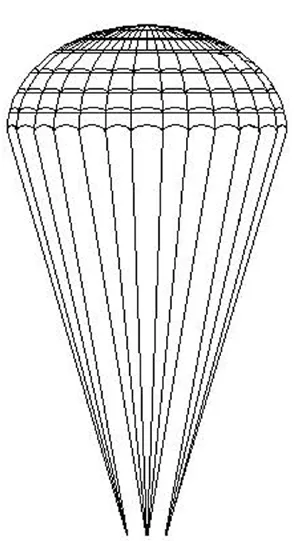
图2 环帆伞示意Fig.2 Gore of the ringsail parachute

本文所研究的对象是群伞系统，以环帆伞单伞构型为基础，构建三伞联合的群伞模型。为了方便进行CFD数值模拟，对环帆伞模型进行简化处理，采用文献[18]的模型处理方式，将10幅帆型结构合并采用相应的球台结构代替，同时忽略降落伞制造材料本身的透气率，只考虑降落伞伞型的结构透气率，因此将降落伞伞衣的边界条件设置为壁面边界条件，入口边界设置为速度入口边界条件，出口设定为压力出口，其初始计算条件如下：海拔H=2 km，速度V=9 m/s，密度ρ=1.006 55 kg/m3，压力P=79 501.4 Pa。采用Pointwise软件对整个计算模型进行非结构网格划分，仿真模型如图 3所示，使用Fluent软件进行流场求解，其中求解方法使用SIMPLE算法，湍流模型使用k-ω两方程模型。

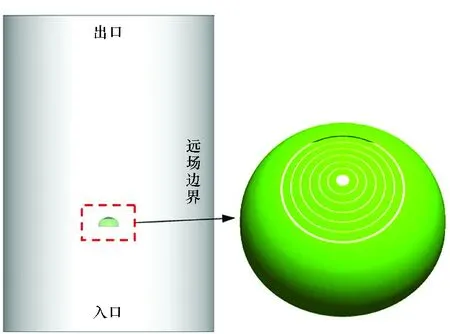
图3 仿真模型示意Fig.3 Schematic diagram of simulation model

2.1.2 单伞仿真结果

本文研究的重点是为了防止单伞之间发生碰撞，结合环帆伞的设计工作，主要改变单伞模型的结构透气量，分析不同结构透气量对群伞系统气动特性的影响。改变结构透气量的主要做法是减小伞衣表面积，即在环帆伞伞衣上“开洞”，但是“开洞”面积不能过大，避免影响环帆伞的阻力面积，因此可以采用的方式包括在伞衣上开窗和增加帆与帆之间的缝隙宽度。

为了对比不同环帆伞的设计构型对整体气动特性的影响，同时验证CFD数值模拟的准确性，在开展群伞系统仿真模拟前首先进行单个环帆伞的仿真分析。模拟的工况包括三种方案：原始构型、开窗构型、开窗/开缝构型，计算模型示意如图4所示，其中原始构型作为基准构型，后两种构型是在原始构型的基础上进行设计更改，环帆伞的伞衣总数为80，每隔5幅进行一处开窗设计，窗口总数为16，而开窗/开缝构型是在开窗的构型下继续进行更改，在环帆伞伞衣的第一帆和第二帆之间进行开缝设计，缝隙的宽度可变。

(a) 原始构型(a) Original

(b) 开窗构型(b) Windows

(c) 开窗/开缝构型(c) Windows/gap图4 降落伞模型伞衣布局设计Fig.4 Illustration of canopy layouts for parachute

采用表1的计算条件对三种不同仿真模型进行数值模拟，为进行有效的数据对比分析，对流场进行切片处理，只显示以X轴为对称轴的流场云图。不同模型流场云图如图5所示。首先对原始构型的流场结果进行描述，如图 5(a)和图5(d)所示，从入口边界到降落伞收口处，压力分布相对稳定，在降落伞内部压力逐渐升高，其伞衣内表面的表压最大值为54.6 Pa；由于环帆伞是利用其伞衣形成较大的阻力面积实现回收载荷的减速着陆，因此在伞衣上方一定的区域内形成较大的低压背风区，并且产生了分离流动现象，此区域内速度和压强均要低于远场来流参数；当气流远离环帆伞伞衣以后，分离流动现场减弱，又逐渐恢复至环境压力和入口速度。

开窗构型是在原始构型的基础上进行开窗修改，其他设计参数保持一致，其流场结果如图5(b)和图5(e)所示，从图中的流场结果可以看出，两者的流场结果基本保持一致，其伞衣内表面表压最大值为54.2 Pa，还可以观察到在窗口处有气流流出，改变了伞衣附近的速度分布。在伞衣上增加窗口对环帆伞的气动特性产生了影响，但效果相对不明显。

开窗/开缝构型是在开窗构型的基础上，在第一和第二帆之间加大了帆与帆之间的缝隙宽度，由原来无缝隙设计改变为每帆宽度各减少10%宽度，其他设计参数保持一致，其流场结果如图5(c)和图5(f)所示，从图中所示的流场结果也可以看出，两者的流场结果基本保持一致，其表压最大值为54.1 Pa，压力值与其他模型的计算结果相近。从以上的模拟结果中可以看出，由于伞衣开窗或者开缝设计对伞衣整体的阻力面积相对较小，三种模型的流场结果趋势大体一致，只是在伞衣局部区域有些区别，因此需要对流场细节及伞衣的气动力进行对比分析。

单伞伞衣表面沿Z轴方向气动力数据如表1所示，由于气流是沿着Z轴正向流动，因此该气动力也是环帆伞所提供的阻力。

从表1中数据可以看出，三种工况下伞衣内外表面的气动力量级相同，数值相差不大，这也和流场云图显示的结果相似，但通过相互比较发现，在原始构型的基础上做出设计修改，开窗/开缝构型模型沿Z轴方向的气动力小于原始构型，说明开窗/开缝构型对伞衣周围的流场产生了影响，单伞的阻力特性随着伞衣面积的减小而降低，但是仍能保持良好的阻力特性。

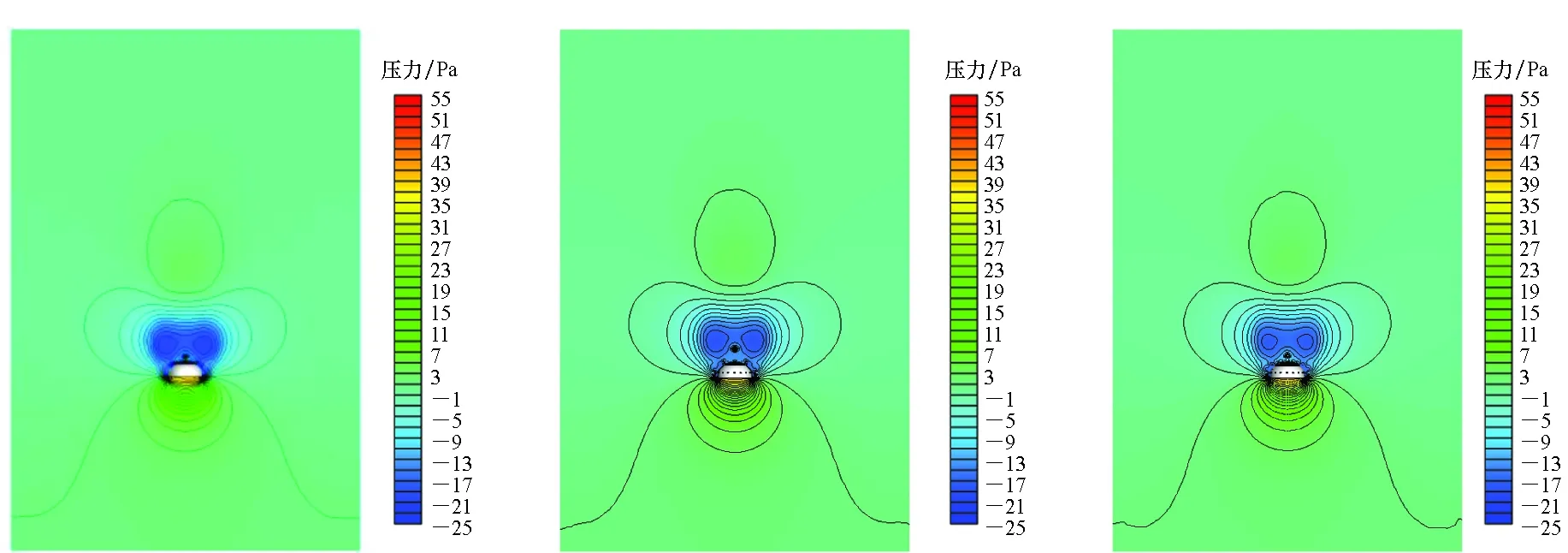
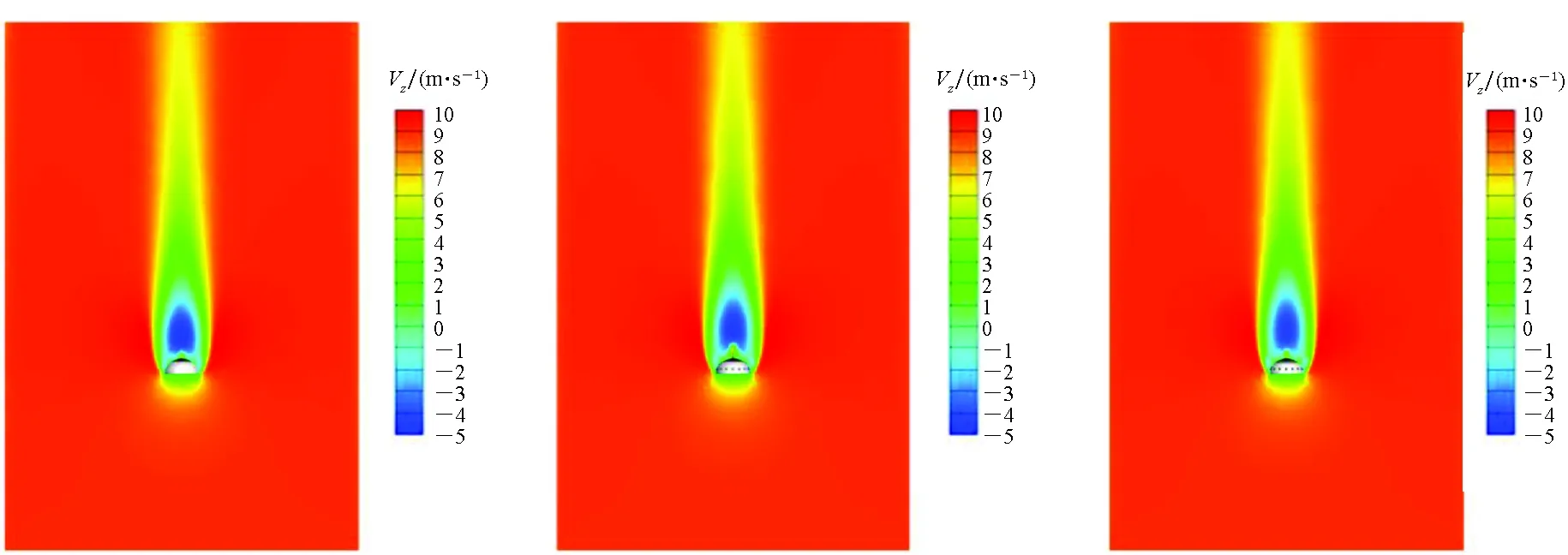
图5 不同模型流场云图Fig.5 Flow fields of different model

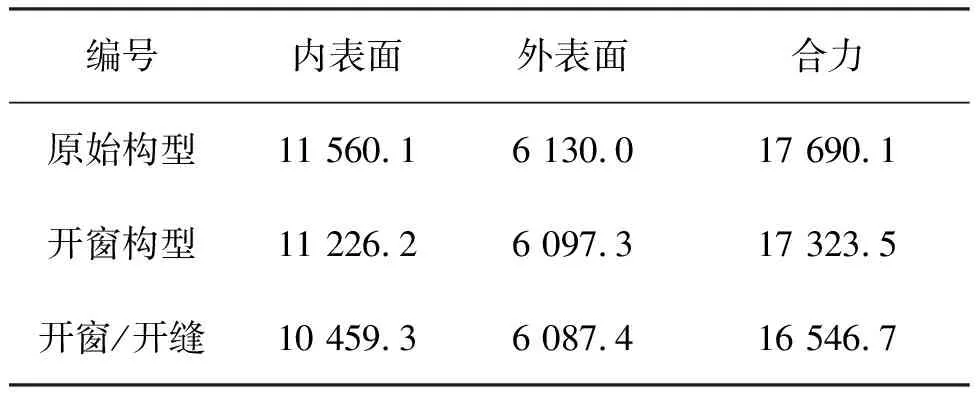
表1 伞衣沿Z轴方向气动力

2.2 群伞仿真模型

群伞仿真模型是由三个单伞模型组合形成，每具单伞沿着各自的轴线旋转一定角度，最终形成的仿真模型如图6所示，其中三具单伞的编号按照顺时针方向设置，群伞仿真中每具单伞的边界条件和单伞仿真模型一致，伞衣的边界条件设置为壁面边界条件，入口边界设置为速度入口边界条件，出口设定为压力出口，其初始计算条件见2.1.1节。由于在计算区域中加入三具单伞模型，因此群伞仿真模型的网格量将成倍增加，仍然使用SIMPLE算法进行流场求解，湍流模型使用k-ω两方程模型。

图6 仿真模型示意Fig.6 Schematic diagram of simulation model

为对比开窗和开缝设计对群伞系统气动特性的影响，总共进行了五个工况的仿真模拟，如表2所示，为保证群伞具有较高的阻力面积，缝隙宽度不宜取过大。

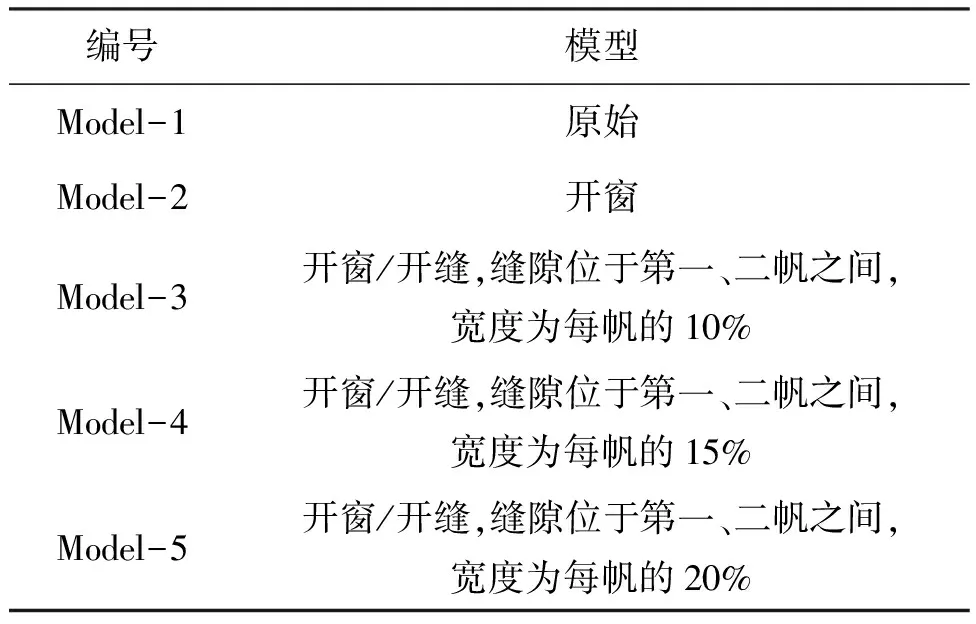
表2 计算模型分类

2.3 群伞仿真结果

相对于单伞仿真模拟，环帆伞只受到外界气流的影响，而群伞系统不仅受到外界气流干扰，同时群伞内单伞与单伞之间也会相互产生影响。在以往群伞空投试验中，就出现过伞与伞之间的碰撞现象，因此群伞系统不仅需要考虑伞衣沿Z轴方向的气动阻力，而且也要分析在不同设计构型下伞衣沿XY平面内的气动特性。

首先对Model-1模型进行流场分析，分别沿群伞系统中不同单伞的对称面进行流场切片处理，得到的流场云图如图7所示。相比于图5所示的单伞流场云图，群伞系统伞衣上方的背风区面积更大，说明在三具单伞的组合影响下，群伞系统的低压流动区域范围更广；在伞衣附近压力等值线更加集中，说明气流通过单伞之间的区域，由于流动区域受到压缩导致气流相互挤压，压力相对集中。在三具单伞中心区域和远离降落伞的区域内，仍然保持远场来流条件，气体流动速度更快，当伞衣背风区内几乎静止的流场在高速气流的带动影响下，在背风区容易出现不对称涡流动现象，靠近伞衣一侧的涡流强度要弱于远离伞衣的一侧。

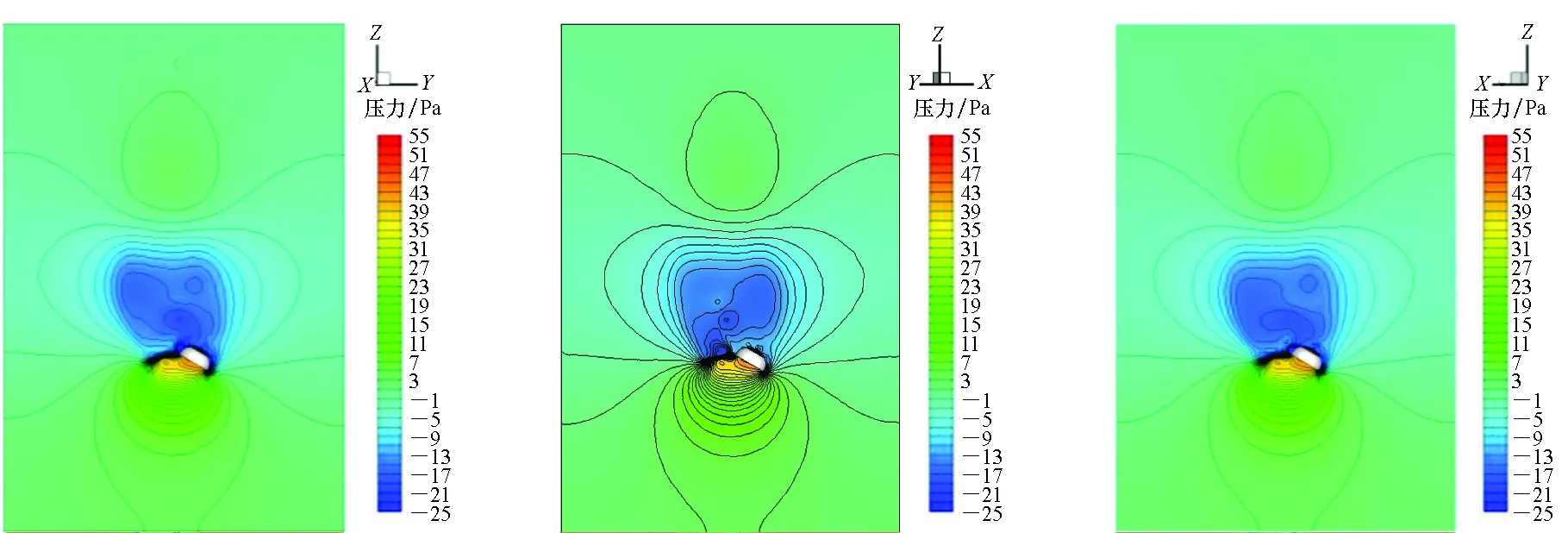
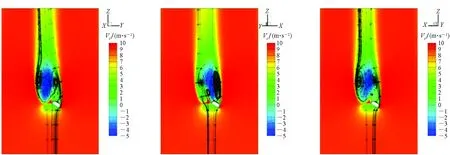
图7 Model-1模型流场云图Fig.7 Flow fields of Model-1

为增强群伞系统在开伞过程中的稳定性，对单伞构型进行优化设计，可选择的一种方案是在伞衣上进行开窗和开缝设计。分别对群伞系统单伞间流场状态和气动力进行分析，比较不同设计构型对群伞系统的性能影响。首先介绍群伞系统的流场特性，其模拟结果如图8所示，其流场结构是由两具单伞对称面切片速度流场组合而成，从图中可以观察到，流场具有较好的对称性，在群伞系统中心区域内，由于气流流动遭遇降落伞伞衣遮挡，受到挤压后的气流在中心区域的流速得到提升，此时该区域内的压力相对于群伞系统外侧的压力要低。由于群伞系统内外侧压力不相等，外侧的高压推动单伞向内侧低压区移动，导致单伞之间的距离逐渐缩小并可能发生相互碰撞。

为避免碰撞现象的发生，其原理是要改变群伞系统中每具单伞所受气动力的合力方向，本文采取的方式是在伞衣上增加开窗/开缝设计，产生上述效果的原因可以通过流场结果进行解释：部分气流从窗口和缝隙之间流出，窗口和缝隙越宽流出的气流越多，流出的气流沿着降落伞伞衣表面的法向与流经中心区域内沿Z轴方向流动的气流形成一定夹角，对该气流具有一定的阻碍作用，导致中心区域内气流速度降低，压力增大。与此同时，从降落伞内部向外流出部分气流，改善了降落伞伞衣附近区域内气流流动的“通畅性”，提高了速度，降低了压力，进而降低了伞衣内外表面的压力差，气动力也随之减小，但是相对于无开窗/开缝模型也丧失了一部分气动阻力。因此，需要对开窗/开缝设计参数的选择进行更加详细的优化设计分析，既要保证降落伞伞衣材料强度和缝纫强度指标，又要满足降落伞的气动阻力性能。

根据群伞系统内三具单伞的气动力仿真数据，显示每种模型下三具单伞在XY平面内的受力，预测每具单伞的运动方向，其示意如图9所示。从图中可以明显地观察到，Model-1模型中每具单伞在XY平面内的运动方向是相对的，每具单伞向系统内侧移动会逐渐缩小单伞间的距离，可能发生相互碰撞的现象；Model-2模型增加了开窗设计，虽然单伞向内侧移动的趋势得到改善，但仍然存在相向运动趋势，没有完全消除碰撞隐患。后三种模型与前两种模型的计算结果区别比较明显，三具主伞都是向群伞系统外侧移动，会逐渐增加单伞间的距离，保证群伞系统工作的稳定性。以上结果表明，增加开窗/开缝设计可以有效改善群伞系统的运动特性，提高系统的安全性。

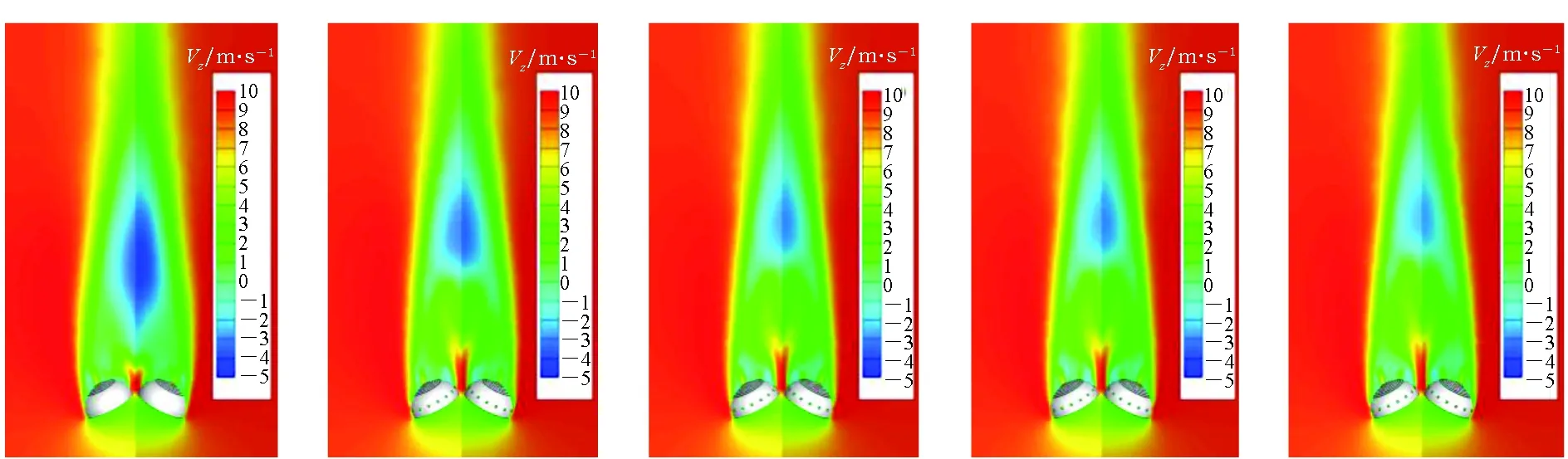
(a) Model-1 (b) Model-2 (c) Model-3 (d) Model-4 (e) Model-5图8 不同模型速度流场云图Fig.8 Velocity flow fields of different model

(a) Model-1 (b) Model-2 (c) Model-3 (d) Model-4 (e) Model-5图9 单伞运动方向示意Fig.9 Schematic diagram of motion direction for parachute

此外，还需对比不同设计构型下群伞系统所能提供的气动阻力，其数据如表3所示。在单伞仿真模拟中，原始模型所能提供的气动阻力是三种模型中最大的，因此在三具单伞组合的条件下所能提供的气动阻力也是群伞仿真模拟中的最大值。在伞衣上增加开窗/开缝设计，虽然减少了单伞伞衣的阻力面积，整个群伞系统损失了部分沿Z轴方向的气动力，但是通过数据对比可以发现，开窗/开缝模型与Model-1模型的阻力占比均保持在93%以上，仍然可以保证群伞系统具有良好的阻力性能。

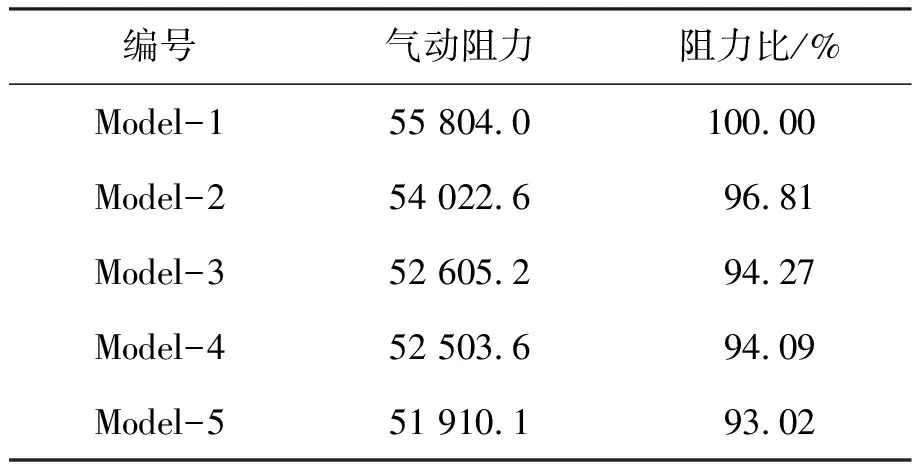
表3 群伞系统的气动阻力

3 结论

本文主要结合群伞构型设计，开展了群伞系统气动特性数值仿真分析工作，在典型环帆伞构型的基础上对单伞伞衣进行开窗/开缝设计优化工作，通过对比多种群伞系统构型仿真结果，验证了本文所采用的开窗/开缝设计可以改变群伞系统附近区域内的流场特性，既增大了群伞系统中心区域流场的压力，又降低了群伞系统外侧的压力，以上两部分压力的变化改变了降落伞本身的受力情况，从最初每具降落伞向中心区域的运动趋势改变为向外侧相对运动，进而降低了发生碰撞的可能性。通过本文的模拟结果可以看出，借助此开窗/开缝优化设计对群伞系统维持其阻力特性并保证群伞系统工作的稳定性等方面，均具有较好的应用效果。

采用数值仿真手段开展降落伞研究工作的优点，一方面可以减少试验数量、提高研制效率和降低风险，另一方面可以掌握群伞系统工作机理、提升设计的准确性、支撑降落伞设计理论发展，促进群伞系统在国家重大型号任务的工程应用。