多核贝叶斯优化的模型决策树算法

高虹雷，门昌骞，王文剑,2

(1. 山西大学 计算机与信息技术学院， 山西 太原 030006；2. 山西大学 计算智能与中文信息处理教育部重点实验室， 山西 太原 030006)

在机器学习中，模型要想达到一个不错的预测结果始终离不开超参数的合理设置。在当前大数据背景下，模型的超参数越来越多，比如神经网络[1]、支持向量机[2]、随机森林[3](random forest，RF)以及极端梯度提升树[4](extreme gradient boosting，XGBoost)、轻量级梯度提升机[5](light gradient boosting machine，LightGBM)等广泛运用于工程领域的模型，这些模型在现实应用中由此带来的问题也层出不穷，比如组合过多，空间复杂，调参费时费力，还可能导致过拟合等问题。针对以上现状，如何高效地进行超参数优化是机器学习领域中至关重要的一个方面。一些算法提出了有效的参数优化方法，例如Falkner等[6]结合贝叶斯优化和赌博机方法的优点提出了一种快速收敛的参数确定方法。Narayan等[7]提出了一个用于超参数优化的开源分布式框架，用户可以灵活定制参数优化方法。此外，Liu等[8]提出一种通用的超参数优化框架，它使用户可以在分布式设置中使用所有可用的计算资源进行模型训练。而贝叶斯优化[9](Bayesian optimization，BO)作为当前超参数优化算法中的主流方法，在自适应机器学习算法[10]、强化学习[11]、自然语言处理[12]、推荐系统[13]、游戏设计[14]、传感器应用[15]、环境监测[16]、医学[17]等应用广泛，相较经验调参方式以及网格搜索[18]、随机搜索[19]等调参算法，贝叶斯优化算法大量降低了训练模型的时间，并且能够自动选择出最优参数，取得了很好的成绩。近年来，对贝叶斯优化算法的研究主要集中在概率代理模型以及效用函数的改进方面[20]。例如，Srinivas等[21]利用置信边界策略重新构造效用函数，接着Desautels等[22]提出批处理置信边界策略使实验可以分批进行。

传统上，多数调参过程凭借经验以及对算法的深刻理解，通过手动选参调参使得模型拥有一个良好的性能，但这种反复实验的方法无法保证能有效地找到最合适的超参数组合，且会耗费大量时间。近年来，超参数优化[23]技术一直被业界积极探索，网格搜索即带有步长的穷举搜索，也是参数选择比较常用的算法之一，但在参数过多的情况下，该算法将会耗费大量的时间，在计算代价上呈指数级上升。而随机搜索则对超参数分布随机采样，且Bergstra和Bengio通过实验证明随机搜索算法[19]比网格搜索更加高效快捷。虽然网格搜索和随机搜索在算法思想上比较简单，在给定的参数范围中测试，以此来确定最优值，理论上网格搜索一定可以找到全局最优值，但在面临参数较多、范围较广的实际情况下，计算代价特别庞大，且两者每次寻找新参数的过程都是独立于之前寻参过程的，即忽略先验分布，随机搜索虽然比网格搜索效率高一些，但同样也无法保证可以得到最优结果。

本文提出一种基于高斯过程的多核贝叶斯优化的模型决策树(model decision tree based on multi-kernel Bayesian optimization, MBOMDT)算法，针对模型决策树算法在构造模型决策树时超参数较多，参数组合复杂，利用网格搜索寻找最优参数费时费力，且不一定能够找到合适的参数值，设计了三种不同类型的核函数作为模型协方差函数组合，以此来应对不同分类数据的特性，实验表明所提算法在参数寻优上要优于传统的模型决策树(model decision tree, MDT)寻优方法，在一定程度上提升了算法的分类性能，节省了大量的调参时间。

1 MBOMDT算法

1.1 MDT算法

文献[24]提出的MDT算法的主要思想为在分类树叶子规模到达给定阈值时停止树的构建，并在生成的不完全决策树的可辨识结点(非叶结点且包含不同类别的样本)上搭载分类器，然后通过分类器继续进行分类，图1为模型决策树的构建示意图。

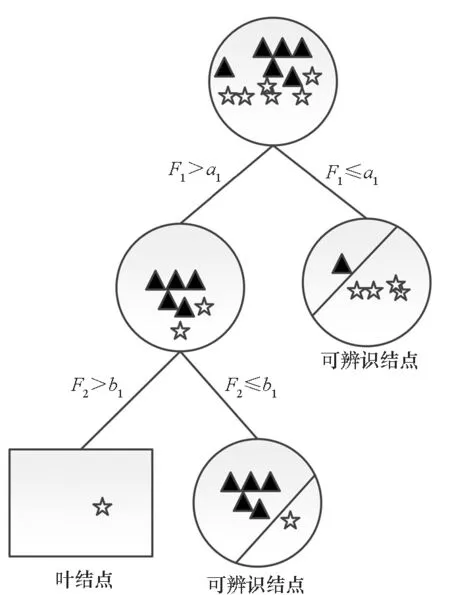
图1 模型决策树构建示意Fig.1 Construction of model decision tree

1.2 多核贝叶斯优化算法

贝叶斯优化核心算法包含两个部分，即概率代理模型及效用函数(utility function)。在MDT算法中，叶子规模以及模型超参数的设置严重影响模型的分类性能。为了减少参数搜索的复杂度以及提升参数选择的稳定性，本文提出了一种MBOMDT算法。

如给定模型决策树MDT，将叶子规模(参数)视为变量，用x表示。将MDT的分类错误率当作目标函数f(x)，则贝叶斯优化的目标是找到恰当的x使得f(x)最小。与网格搜索或随机搜索不同，贝叶斯优化在选择下一个观测点时考虑了已有的观测点。具体来说,给定x的已有观测点集合X={x1,x2,…,xn}以及目标函数值集合Y={y1,y2,…,yn}，贝叶斯优化利用集合Y、X以及概率代理模型拟合真实目标函数f(x)，之后根据效用函数得到下一个观测点，并将观测点及其目标函数值分别放入集合X与Y中，更新概率代理模型。重复上述过程，直到满足终止条件，此时得到最优参数值。

f(x)～GP(M(x),Σ)

(1)

假设集合X、Y在忽视噪声的情况下，即y=f(x),Y服从联合高斯分布N(M(X),Σ)，并且协方差函数可由核矩阵K(X,X′)替代，公式如下：

(2)

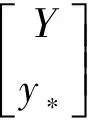
(3)

k(X,x*)表示x*与X之间的3×1阶核矩阵。通过以下公式可以形式化地表达上述过程：

p(y*|X,Y,x*)=N(M*,Σ*)

(4)

其中，Σ*=k(x*,x*)-k(x*,X)k(X,X)-1k(X,x*)，M*=k(x*,X)k(X,X)-1Y。最终，通过上述过程可以对目标函数进行拟合。

效用函数则起到了确定下一估计点的作用，常用的效用函数有：提升概率最大评估点[26](probability of improvement，POI)、最大化期望增量[27](expected improvement，EI)、最大化高斯过程置信区间[28](GP upper confidence bound，GP-UCB)。其中，GP-UCB表达式为：

(5)

参数β用来权衡均值及协方差，本文实验中选择的效用函数即GP-UCB。

由式(1)可知，构建函数分布的能力以及理想的预测结果很大程度上依赖于协方差函数，即核函数的选取。此外，对于多信息源、多模态数据，如果可以结合多个单核函数，可以提升模型辨识能力，即多核学习算法[29]。本文运用多核学习算法的思想，通过使用不同的核函数来提升算法性能。实验所使用的径向基函数(radial basis function, RBF)核函数分别表示为：

百分比是玉米粉碎后7目上，7～18目，18目下分别占玉米总重量的百分比。经不同工艺进行玉米粉碎，并对粉碎后粒度的分布情况统计分析如表2。

(6)

(7)

(8)

为更好地理解贝叶斯优化过程，本文给出一个例子进行说明，假设目标函数为f(x)=sinxcosx+1/(x2+1)，图2分别为使用RBF核、Matern核以及DotProduct核的贝叶斯优化过程示意图，每个实验迭代10次。

由图2可以看出，在后验分布中方差越小的点代表越接近真实分布，接下来通过最大化效用函数，将下一评估点选出，即图2中星点所在的位置，通过多次迭代过程，找到目标函数的最大值也即待调参数全局最优值。通过图2中不同核函数对同一目标函数进行优化可以得出，在寻优的过程中，使用不同核函数拟合出的后验分布具有不同的分布特性，当使用核函数组合来进行这一操作时，可以更大程度地覆盖没有被考虑的情况，提升算法整体的性能。多核贝叶斯优化算法如算法1所示。

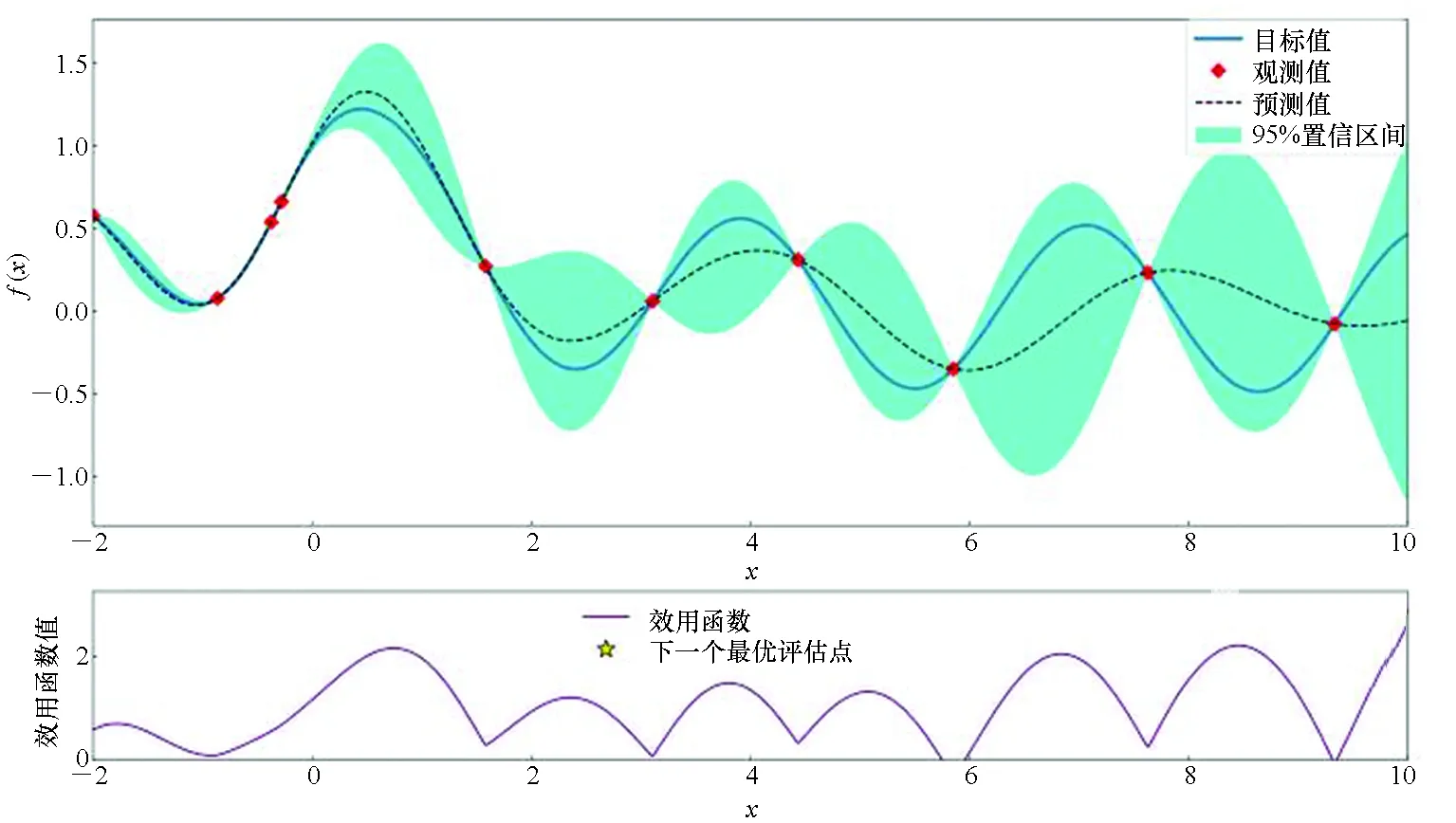
(a) RBF核(a) RBF kernel

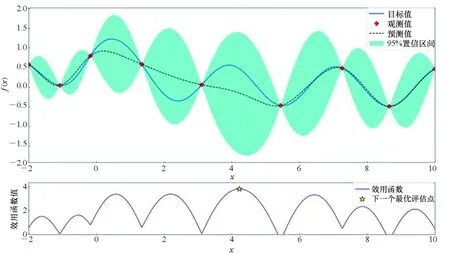
(b) Matern核(b) Matern kernel

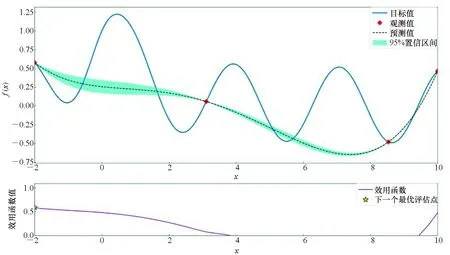
(c) DotProduct核(c) DotProduct kernel图2 贝叶斯优化模型Fig.2 Bayesian optimization model

2 实验结果及分析

2.1 实验数据集及实验设置

实验所用13个分类数据集均来自UCI数据集，如表1所示。计算机硬件及环境配置为：Intel(R)Core(TM)i7-7700 3.60 GHz 处理器，内存为16.0 GB，Windows 10 操作系统，Python 3.7 版本。

算法1 多核贝叶斯优化算法

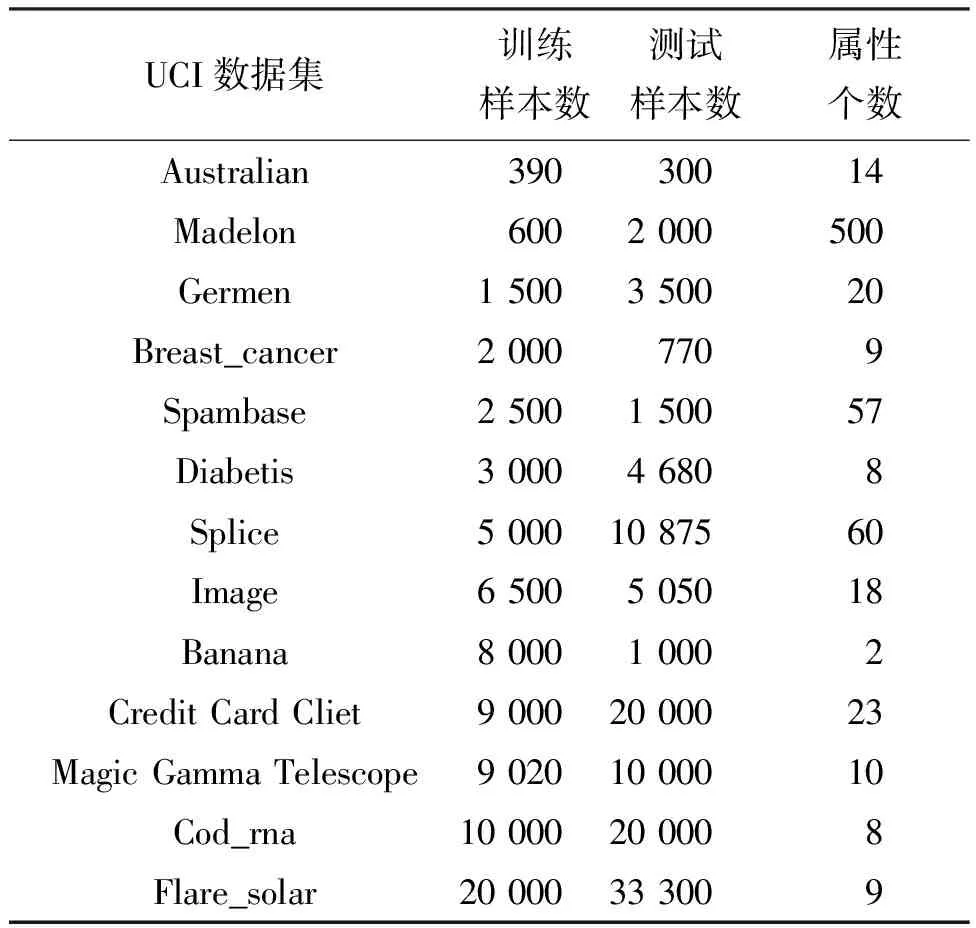
表1 实验数据集

MBOMDT算法选用了软件包LIBLINEAR模型和标准支持向量机(support vector machine, SVM)模型，创建出三种新的模型，其中使用了LIBLINEAR模型的记为MBOMDT_LIB，使用线性核的SVM模型记为MBOMDT_SVM(linear)，使用高斯核的SVM模型记为MBOMDT_SVM(rbf)。

实验中的超参数分别为可辨识结点样本个数阈值V、LIBLINEAR中的类型参数s、SVM中惩罚参数c、高斯核参数γ。实验内容主要为通过改进的贝叶斯优化算法对模型决策树超参数进行调参，以期得到直观明确的最优参数值，其中因为LIBLINEAR模型的参数s为类型参数，故在涉及使用LIBLINEAR模型的算法中类型参数s统一设置为2，不再另做讨论。实验中所用到的6种算法的相关参数如表2所示，MDT相关算法实验参数设置来自文献[24]。

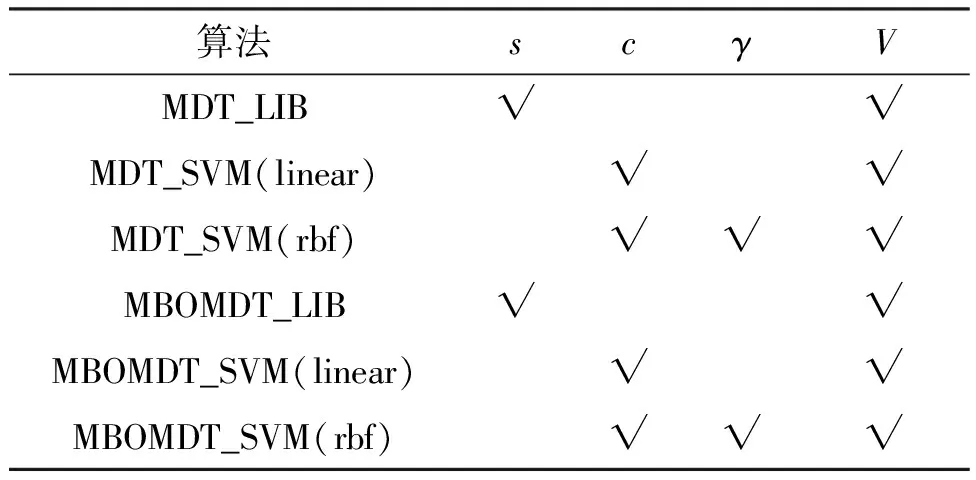
表2 各算法实验参数一览表

文献[24]中提出的三种模型决策树算法MDT_LIB、MDT_SVM(linear)和MDT_SVM(rbf) 的超参数较多、调参过程费时费力，且三种算法已与SVM、KNN、LR(logistic regression)、LIBLINEAR等几种常用的分类方法进行了比较，实验结果表明文献[24]中提出的三种模型决策树算法在分类错误率及运行时间上大多优于其他方法，因此，本文所提三种模型将与文献[24]中提出的三种模型决策树算法以及原始贝叶斯优化下的模型决策树BOMDT_LIB算法、BOMDT_SVM(linear)算法、BOMDT_SVM(rbf)算法进行比较。

2.2 算法参数的优化

MDT算法通过实验探究了可辨识结点样本个数阈值V对实验结果的影响，即调整参数V的大小以期找到实验结果的最优值，并作为算法的最优参数值进行下一步的分类研究。其方案为令可辨识结点样本个数阈值V分别取样本数的10%、30%、50%、70%、90%并在不同数据集上进行实验，找到相对较优参数值，SVM模型中的惩罚参数c、高斯核参数γ均为人工调参并结合经验设定的固定值。其中：MDT_LIB算法除在Credit Card Cliet和Cod_rna数据集上V取训练样本数的30%，在Spambase数据集上V取训练样本数的90%外，其余算法中V均为训练样本数的10%。MDT_SVM(linear)算法除在Spambase和Cod_rna数据集上V取训练样本数的50%，在Credit Card Cliet数据集上V取训练样本数的70%外，其余算法中V均为训练样本数的10%。MDT_SVM(rbf)算法除在Germen数据集上V取训练样本数的50%，在Image、Magic Gamma Telescope以及Cod_rna数据集上V取训练样本数的70%，在Credit Card Cliet数据集上V取训练样本数的90%以外，其余算法中V均为训练样本数的10%。使用线性核SVM模型中的惩罚参数c均为1，使用高斯核SVM模型算法中的惩罚参数c均为1、高斯核参数γ均为0.5。相应地，本文通过改进贝叶斯优化算法对模型决策树进行参数选择，各参数范围分别是：V∈(0,100)、c∈(1,50)、γ∈(0.01,1)，算法首先选取3个初始点，总计迭代次数为20次。通过实验为每种模型优化后的参数如表3所示。

在参数寻优的过程中，通过实验可以看出：各算法基本迭代次数为10次以内就可将综合范围内的最优参数值找到。因此，利用改进的贝叶斯优化方法寻优可大幅减少原算法训练最优参数的时间，提高算法分类效率。当使用LIBLINEAR模型时，算法参数为V。不同算法下运行时间比较如表4所示。MDT算法从{1,5,10,…,100}中寻找V的最优值，MBOMDT算法从(1,100)中寻找V的最优值，从表4中可以看到MBOMDT算法选择参数的时间明显低于MDT算法。另外，当使用高斯核SVM模型时，MDT算法分别从{1,5,10,…,100}、{1,10,20,…,50}、{0.01,0.1,0.2,…,1}中寻找V、c、γ的最优值，而MBOMDT算法从(1,100)、(1,50)、(0.01,1)中寻找参数值，从表4还可以看出MBOMDT的参数寻优时间远低于MDT，其中“/”表示时间超于24 h。

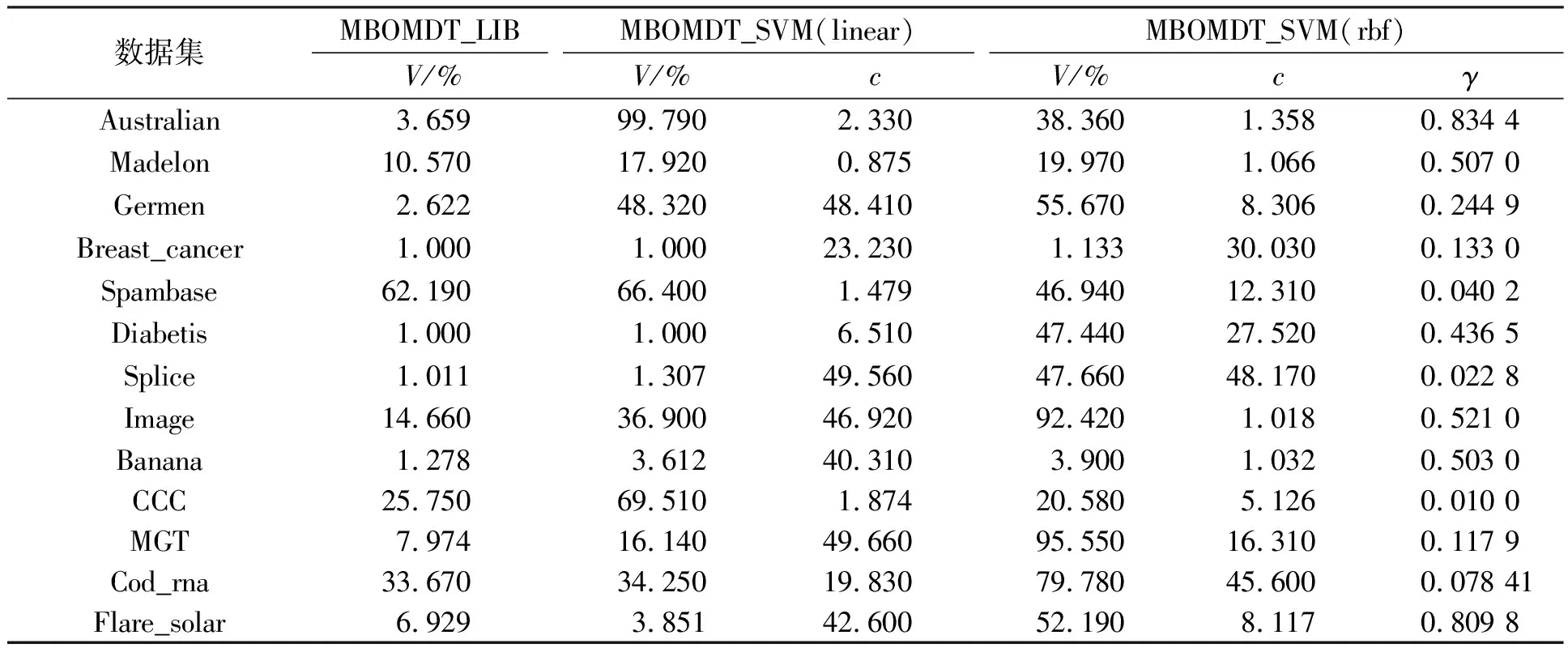
表3 MBOMDT算法下参数的最优值

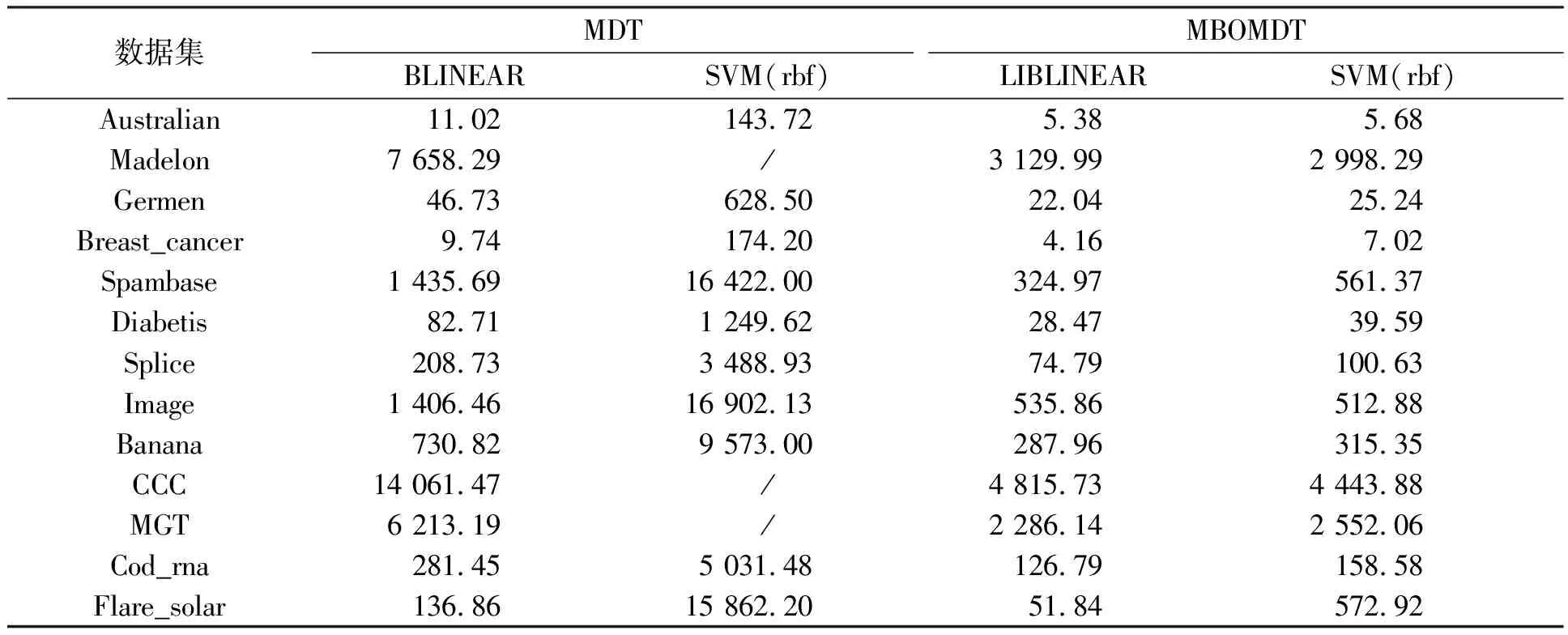
表4 不同算法下运行时间比较结果

2.3 本文算法与MDT算法的比较

本节将本文提出的三种算法MBOMDT_LIB、MBOMDT_SVM(linear)以及MBOMDT_SVM(rbf)分别与文献[24]中的MDT_LIB、MDT_SVM(linear)和MDT_SVM(rbf)三种算法进行分类性能的比较，实验结果如表5所示。MDT三种算法在部分数据集上的实验结果来自文献[24]，本文所提算法中的最优超参数设定均依照表3所得结果设置。由表5可知，本文所提三种算法在得到最优参数值之后使得算法的分类性能与之前对应的MDT算法相比，均得到了提升，其中MBOMDT_SVM(rbf)算法在所有算法中表现最好，表中标黑数据为该数据集下6种算法分类错误率最小值。

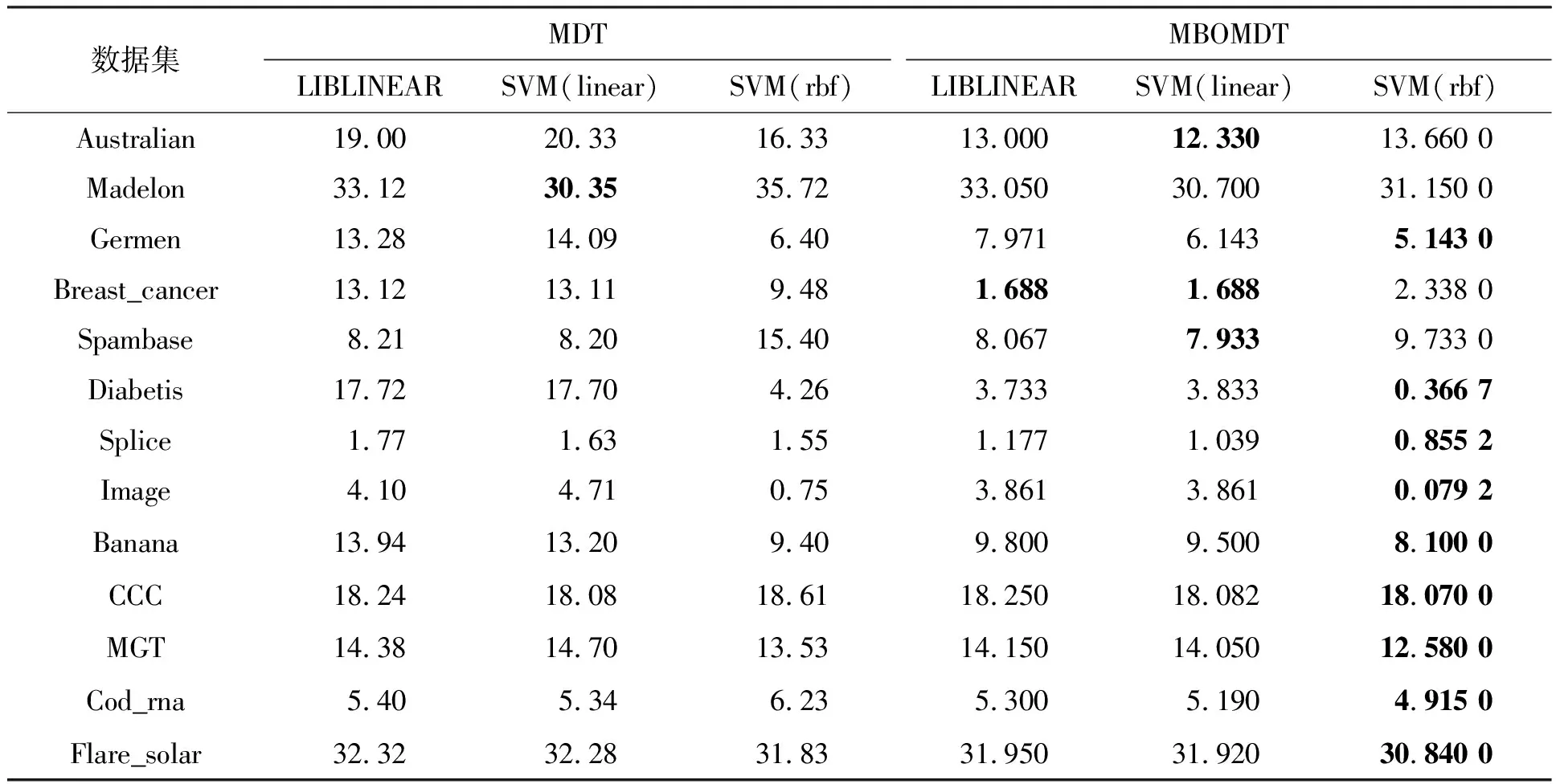
表5 不同算法下分类错误率比较结果

为直观地理解实验结果，图3给出了MBOMDT算法与MDT算法采用三种不同分类器时分类错误率的大小关系比较。其中，黑点表示所用的13个数据集，横坐标代表MDT算法的错误率，纵坐标代表MBOMDT算法的错误率。对角线上的黑点表示两种算法错误率一致或基本相同，在对角线上方的黑点表示在此数据集上MBOMDT算法错误率高于MDT算法错误率，对角线下方的黑点代表在此数据集上MBOMDT算法错误率低于MDT算法错误率。黑点距离对角线越远，表示在此数据集上两种算法的分类错误率相差越大。

由图3可知，当采用LIBLINEAR模型时，在5个数据集上MBOMDT的错误率明显低于MDT算法，且提升幅度较大，其余数据集上基本持平或稍好于原结果；当采用SVM(linear)模型时，同样5个数据集上MBOMDT算法的错误率明显低于MDT算法，5个数据集上有小幅度提升，2个数据集基本持平，只有在1个数据集上略低于MDT算法；当采用SVM(rbf)模型时，MBOMDT算法只有在其中1个数据集上的结果与MDT算法基本持平，在剩下的数据集上，表现均有明显提升。特别地，在Diabetis数据集上MBOMDT_SVM(rbf)算法的分类错误率比MDT_SVM(rbf)算法降低了91%。综上，MBOMDT算法可通过找到全局最优超参数使模型分类的性能得到进一步提升。

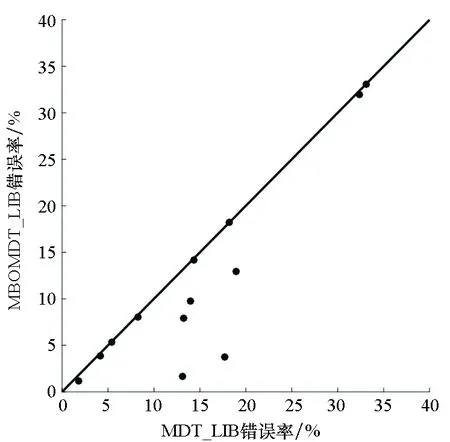
(a) LIBLINEAR

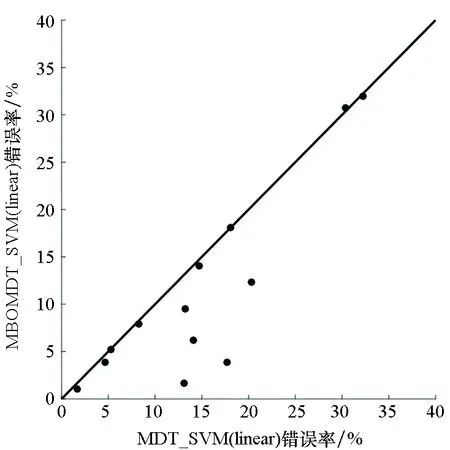
(b) SVM(linear)

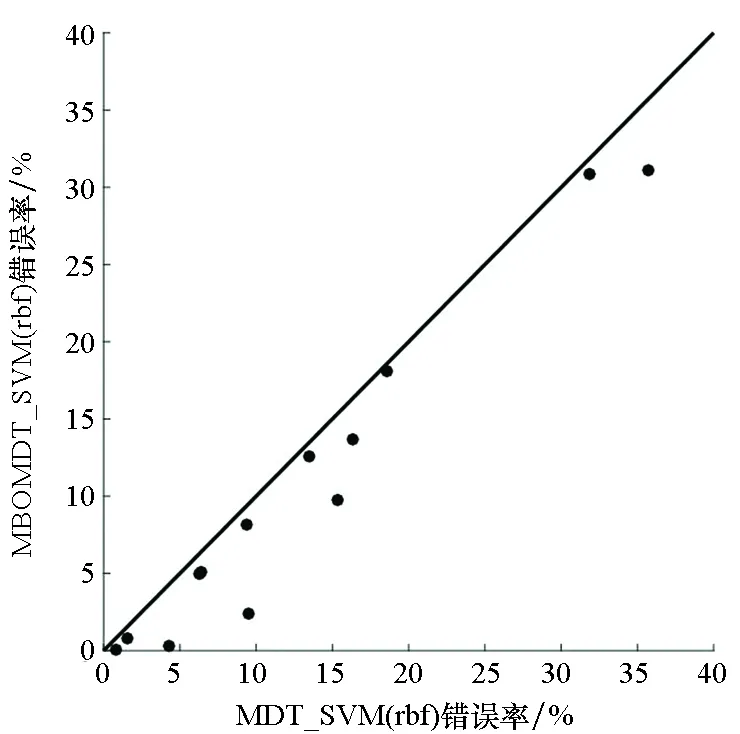
(c) SVM(rbf)图3 MBOMDT与MDT分类错误率比较Fig.3 Comparison of classification error rate for MBOMDT and MDT

2.4 本文算法与BOMDT算法的比较

本节将本文所提出的三种算法MBOMDT_LIB、MBOMDT_SVM(linear)以及MBOMDT_SVM(rbf)与使用原始贝叶斯优化后的模型决策树BOMDT_LIB、BOMDT_SVM(linear)和BOMDT_SVM(rbf)三种算法进行分类性能的比较。各算法均在最优超参数下运行，结果如表6所示。

由表6可知，MBOMDT_SVM(rbf)算法表现最好，表中标黑数据为该数据集下6种算法分类错误率最小值。从表中可以看出，三种MBOMDT算法在绝大部分数据集上的分类性能均优于BOMDT算法，这说明使用三种不同类型的核函数作为模型协方差函数组合要优于单一核函数下的贝叶斯优化算法，实验结果表明，本文所提算法可应对不同分类数据的特性，从而获得了较为理想的模型预测性能。

图4给出了MBOMDT算法与BOMDT算法采用三种不同分类器时分类错误率的大小关系比较。由图4可知，只有采用SVM(linear)模型时，在1个数据集上略低于BOMDT算法，其他算法均好于或与BOMDT算法相当。特别地，在Image数据集上MBOMDT_SVM(rbf)算法的分类错误率比BOMDT_SVM(rbf)算法降低了73%。综上，MBOMDT算法通过在高斯过程中构建三个核函数组合，对分类问题适用更加广泛，且在一定程度上可以提升模型的分类性能。

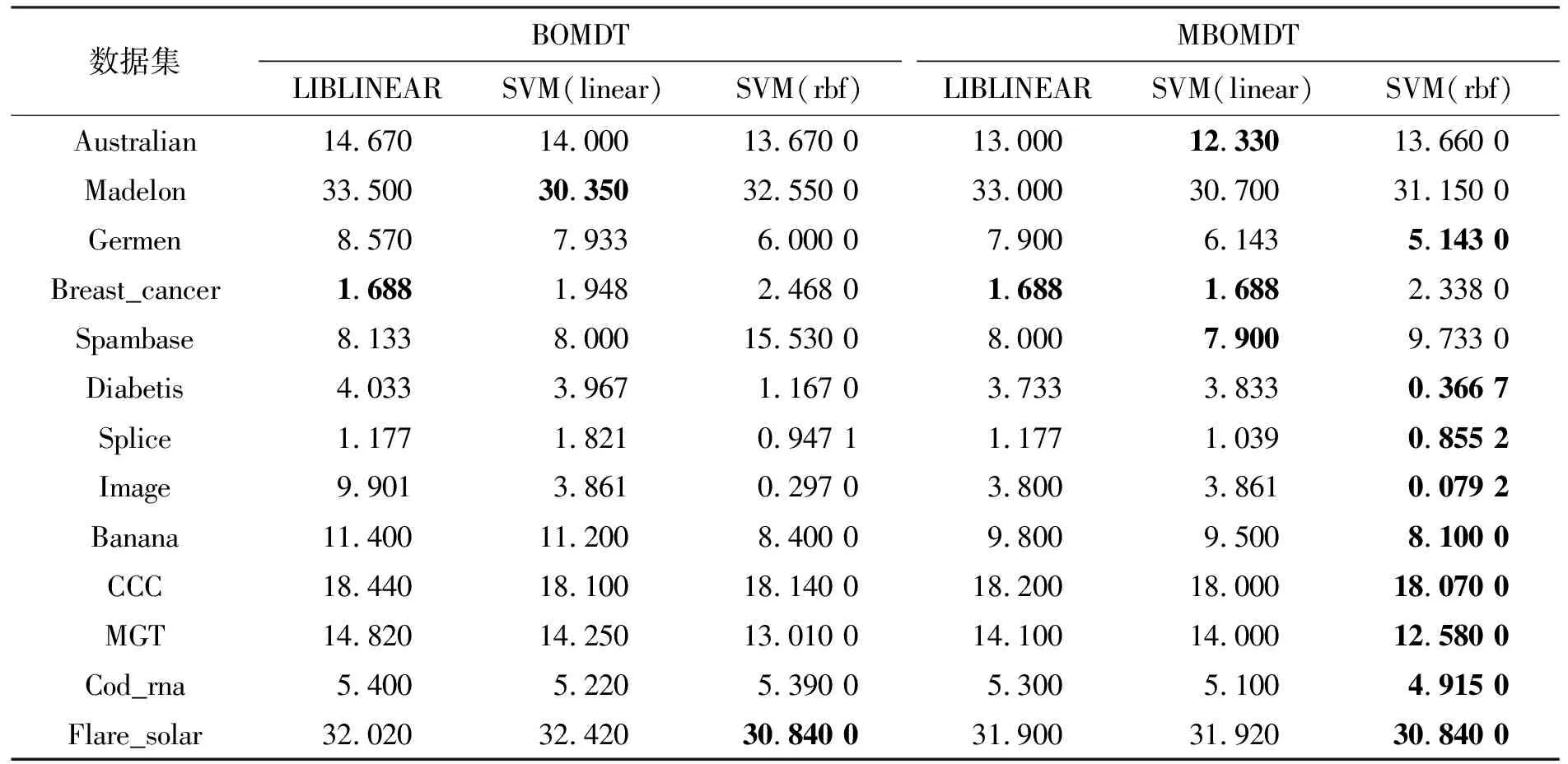
表6 不同算法下分类错误率比较结果

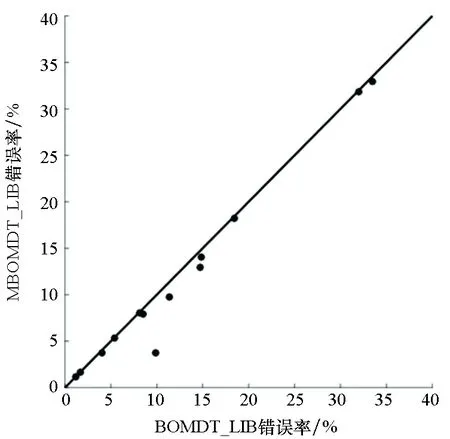
(a) LIBLINEAR

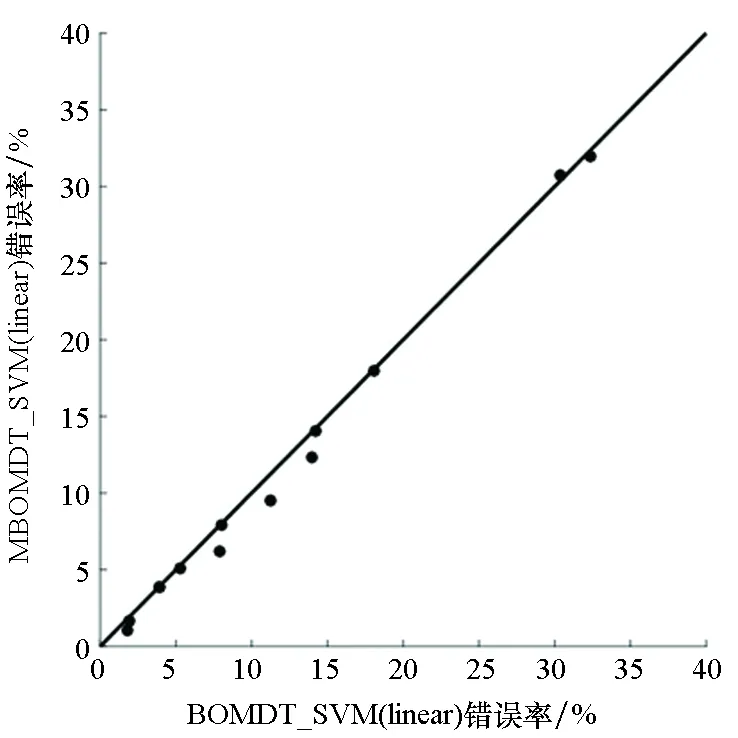
(b) SVM(linear)

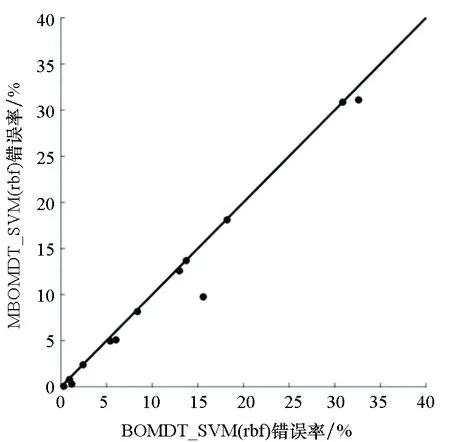
(c) SVM(rbf)图4 MBOMDT与BOMDT分类错误率比较Fig.4 Comparison of classification error rate for MBOMDT and BOMDT

3 结论

本文提出一种多核贝叶斯优化的模型决策树算法，算法采用三种不同的高斯过程建模寻优，以应对不同的分类数据特性，利用贝叶斯优化技术，不断加入新的信息，找到新的后验分布，选出最佳的参数组合。实验表明，所提算法在参数寻优上要优于传统的MDT寻优方法，能够在迭代次数不多的情况下找到更优的参数值，且在一定程度上提升算法的分类性能，减少计算代价。不过多核贝叶斯优化的模型决策树算法对数据维度和算力要求方面比较高，在未来的工作中，需研究数据降维对算法的影响，以增强本算法的适用性。