众包标签的双重置信度推断算法

张 琳，姜高霞，王文剑

(山西大学 计算机与信息技术学院， 山西 太原 030006)

机器学习是现代计算机快速发展的领域之一，涉及各个领域的应用。目前，研究人员在深度学习方面取得了很多成果，但其可解释性依然是难以解决的问题。因此，人在机器学习中的作用依然不可忽视。众所周知，传统的数据注释依赖于领域专家，成本高且耗时长，其限制了标签数据集的获得。而随着众包系统的快速发展，标签数据的获取变得比较容易，但由于收集的标签中存在噪声，众包数据训练的学习模型质量通常低于专家标记数据训练的模型。直观上，学习模型的质量与标签的质量密切相关，因此提高标签质量是提高学习模型质量的一个直接途径。

在众包平台获取带噪声的标签数据集后，通过设计算法，从多个标签集合中归纳出一个完整的标签，这些算法被称为真相推理算法(ground truth inference algorithms)。在不知道某实例真实标签的情况下，一般使用真相推理算法推断其真实标签，但单纯的推理算法的学习是相对困难的。因此，利用实例数据分布信息帮助推理算法推断真实标签十分重要，且希望每个实例的集成标签为其真实标签。

使用重复标签来提高标签质量可以追溯到20多年前，Smyth等在1994年使用极大似然估计算法和重复标记去解决金星图像标记的不确定性[1]。多人投票机制(majority vote，MV)是一种最简单高效的方法，除了MV算法，近几年还提出了一些其他的推理算法。这些推理算法可以根据其数学方法分为两类：基于机器学习的算法和基于线性代数的方法。基于机器学习的方法是当前研究的主流，早在1979年，Dawid等提出了一种基于最大似然估计的真相推理算法(Dawid-Skene model，DS)[2]，除了为每个例子推断出集成标签外，DS还为每个贴标签者估计了混淆矩阵；Demartini等提出的ZenCrowd[3]算法通过对标记者质量建模来确定每个样本属于特定类的概率，但其没有关注任务难度；而Whitehill等提出的GLAD[4]算法则在此基础上，对任务难度建模，将此结果应用到对标记者质量的建模中，使推断结果具有更高的准确性，但导致其代码运行迭代过程十分缓慢。Sheng等和Ipeirotis等分别于2008年和2014年在研究了MV算法后，提出了简单的概率模型来描述单样本的标签质量[5-6]，但其假设每个标签的质量均相同。Jung等在2011年针对实例，提出了一种利用评分机制和权重提高MV精度的方法[7]，其中推理模型通常是基于概率图形模型，在概率图形模型中进行推理的一种重要的主流通用方法是期望最大化(expectation-maximization，EM)算法。2014年Li等在DS模型下推导了具有任意有限标记者和项目数的一般类型聚合规则的错误率边界[8]，可用于设计最优加权多数投票。Khetan等在2016年也分析了广义DS模型下众包的可靠性[9]。在基于DS改进的模型中，当类的数量较大而标签的数量较少时，会造成混淆矩阵十分稀疏。

众包通常基于两个基本的共同假设：贴标签者有不同的可靠性，并且独立做决定。一些推理算法只遵循这些假设，例如DS和ZenCrowd。而Raykar等[10]还基于标签标记者在提供标签时的偏见，IEThresh[11]则是基于了学习者的经验，正标签阈值(positive label frequency threshold，PLAT)[12]方法假设标签者对消极和积极的例子有不同的校正率，LC-ME[13]算法假设每个项都属于一个潜在类，标签程序对同一类的项具有一致的视图，但对不同类的项具有不一致的视图。

由于仅根据带噪音的标签推断实例的真实标签比较困难，因此除了一般的真相推理算法外，近几年一些学者提出了根据实例特征和标记者影响等因素去提高标签集成效果的方法。Tian等在2018年提出了M3V算法[14]，Ruiz等在2018年提出了一种通过变分高斯过程从众包中学习正确标签的方法[15]。还有一些学者提出不学习真相推理算法，而直接根据带噪音的标签集学习分类算法。另一些学者利用多任务学习方法去处理众包标签噪音，也取得了不错的效果。目前来看，利用其他信息提高众包标签集的集成算法效果是可行的。但现有的算法在多分类问题中的表现相对较差，且在众包系统中获取标签时，标记者越少代价越小，因此希望可以在获取的众包标签数较少的情况下得到较优的标签推断结果。由此考虑使用聚类算法研究众包噪音标签过滤问题。本文提出的算法主要通过对实例特征聚类及分析标记者相似性两部分来提高标签推断的准确率。

1 单标记众包标签的双重置信度算法

1.1 问题描述

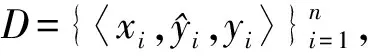
1.2 双重置信度计算方法

由于提高集成标签的质量面临巨大的挑战，许多研究人员试图在标签聚合过程中引入更多的先验信息，这些方法违反了通用标签聚合的不可知前提，即除了收集的噪声标签外，不能使用任何先验知识。实例的特征携带有价值的信息，如果可以应用适当的机器学习方法，这些特征可以帮助识别和分类这些项目。因此，在标签推断过程中完全忽略实例的特征是不明智的，且应用特征并不违反不可知论的先决条件。

本文算法主要通过设置标记者置信度推断实例的集成标签。标记者置信度由两部分确定：第一部分是通过聚类算法将实例的特征部分聚类，再根据聚类结果和标记者提供的标签，确定每位标记者的正确率，从而得到标记者置信度的第一部分基于数据分布特征的置信度；第二部分通过计算标记者提供的标签间的相似度得到基于标记信息的置信度，若某位标记者与其他标记者提供的结果越相似，则其置信度越高。将两部分置信度合并，由此得到完整的标记者置信度。

1.2.1 基于数据分布特征的置信度

通过对数据特征执行聚类算法得到基于数据分布特征的置信度。通常数据集中大多数的数据标记问题是较为简单的，标记者可以较容易地为这些问题打出正确的标签，而对于较为困难的一部分数据，标记者所提供的标签很有可能是错误的，这时可以通过聚类结果与某一组标签的一致性来确定某个标记者的置信度，从而提高标签推断结果的准确率。

图1通过一个简单的例子来说明聚类置信度的可行性。图中圆形、正方形、三角形分别表示3类数据，图1(a)表示数据的真实分布情况，图2(b)表示标记者w1提供的数据划分结果，图1(c)表示另一标记者w2提供的数据划分结果，图1(d)表示将原始数据进行聚类得到的分类结果。

图1中两位标记者在为众包数据提供标签时均存在错误标签，而此时有较为可靠的聚类结果，则可利用这一结果帮助确定标记者的置信度。

由于采用了聚类算法，因此聚类结果与众包标记结果的相似性采用常见的聚类评价指标Rand Index系数表示，将其作为标记者的第一部分置信度：

(1)

式中：Tp表示在聚类结果和标记者提供的标签中均属于同一类的实例数；Tn表示在聚类结果和标记者提供的标签中均不属于同一类的实例数；Fp表示聚类结果属于一类，而标记者提供的标签不属于一类的实例数；Fn表示聚类结果不属于一类，而标记者提供的标签属于一类的实例数；n表示实例数。

1.2.2 基于标签信息的置信度

在众包数据中，某位标记者与其他标记者所提供的标签信息越相似，则这位标记者提供的标签越可信。因此，将标记者之间的相似性作为标记者置信度的一部分，用以计算完整的置信度。

用pab表示标记者a与标记者b所提供的标签信息间的相似度，pa表示标记者a与其他标记者的平均相似度，a,b∈(1,m)。

(2)

(3)

根据上文分别得到基于数据分布特征和标签信息的置信度v1和v2，v1,v2∈(0,1)，计算两者的几何平均值V，即标记者置信度，其中V∈(0,1)。

(4)

图2所示为标记者置信度V随v1、v2变化的趋势图。由图可知，v1、v2均对V有整体的影响。

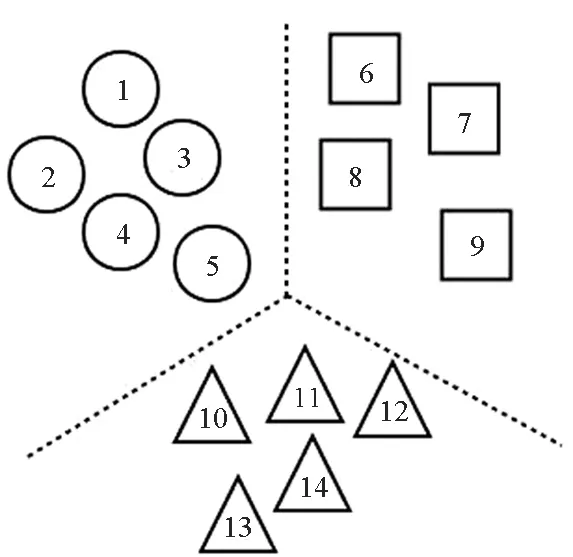
(a) 原始数据的分布(a) Original data distribution

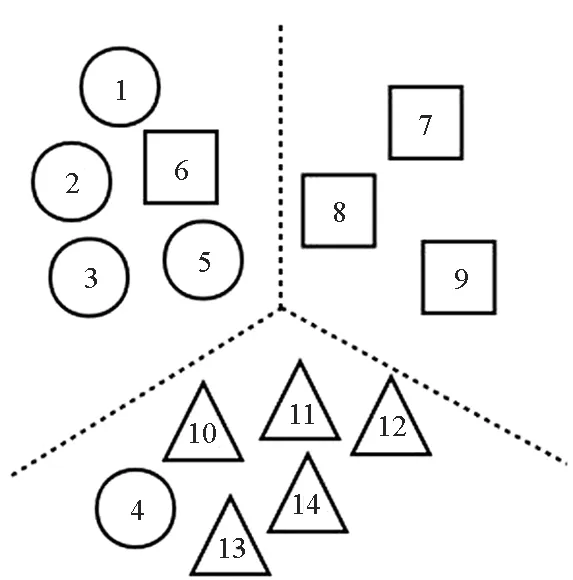
(b) w1的数据划分结果(b) Data partitioning results of w1

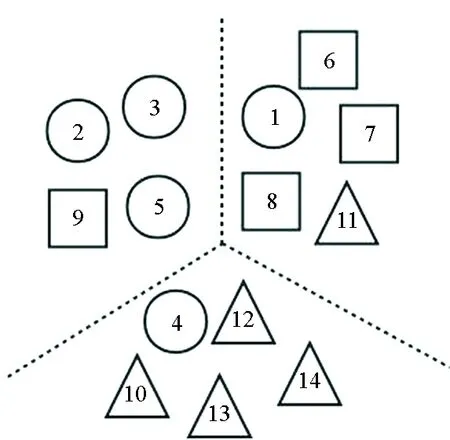
(c) w2的数据划分结果(c) Data partitioning results of w2

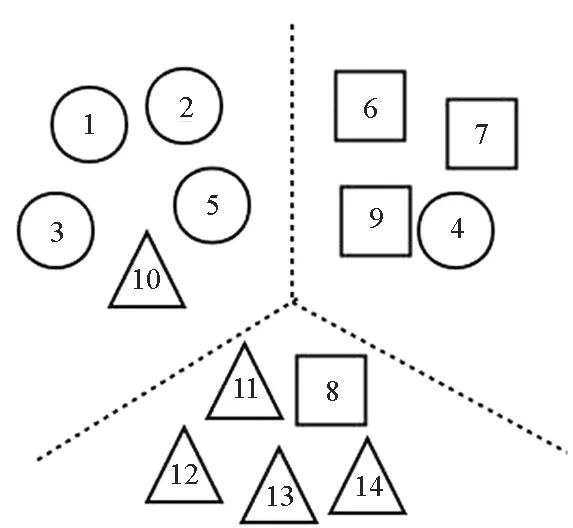
(d) 数据聚类结果(d) Data clustering results图1 数据标记Fig.1 Data labeling

若使用算数平均值，则当其中一个变量不变时，另一变量对其整体的影响有限，不能充分表现变量较小时对整体权重的影响。

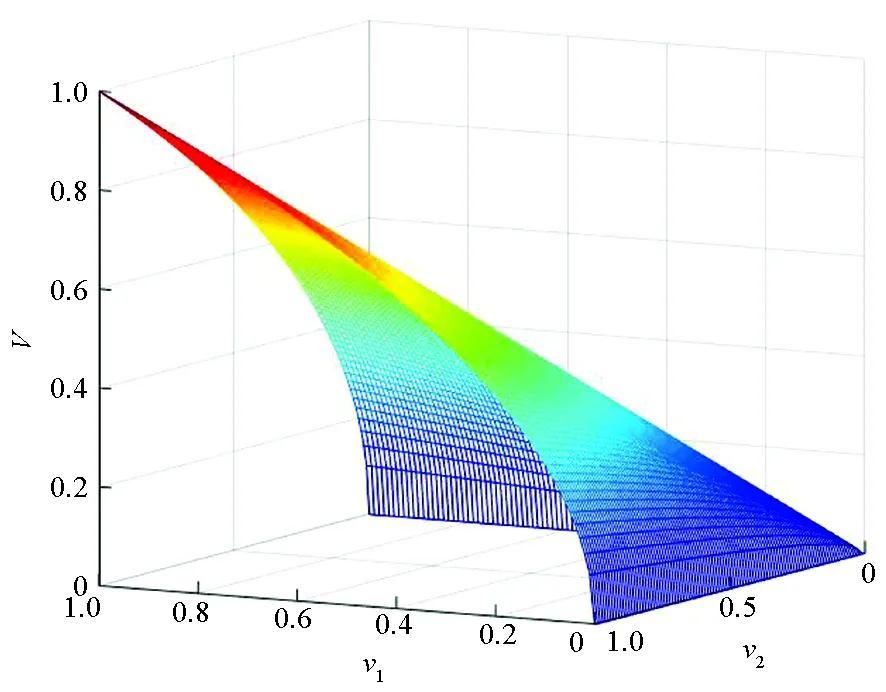
图2 置信度的变化情况Fig.2 Variation of confidence

根据得到的标记者置信度推断得出实例的真实标签：

(5)

式中，p(li)表示实例推断标签为li的可能性，i∈(1,k)。

双重置信度推断(double confidence inference，DC)算法的步骤如算法1所示。

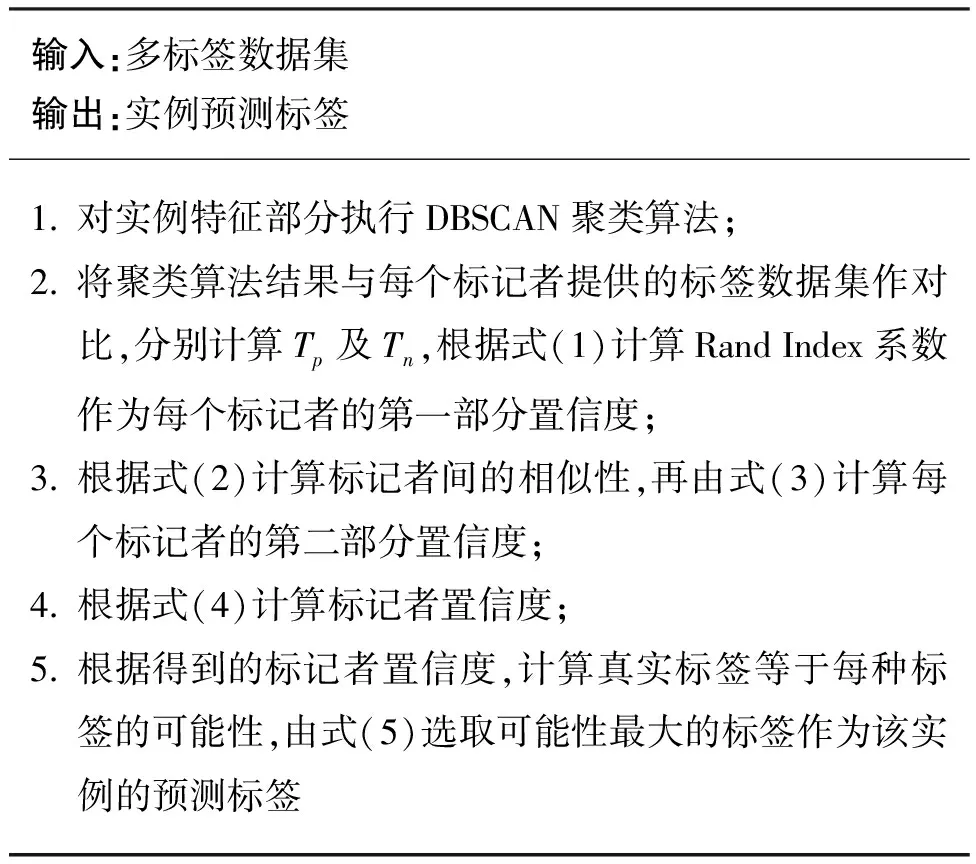
算法1 双重置信度推断算法

本文算法在每个数据集上的每种标记数下的计算复杂度O(n)=n·p·l，其主要由算法1的第5步推断实例的真实标签过程产生。其中：n为数据集实例数；p表示标记数，即为该实例提供标签的人数；l为数据集的类数。

2 实验与分析

本节对表1所示的10个真实世界数据集进行实验，并与4种经典的方法MV、DS、GLAD、ZC算法在标签推断准确率和时间效率两方面进行了比较。

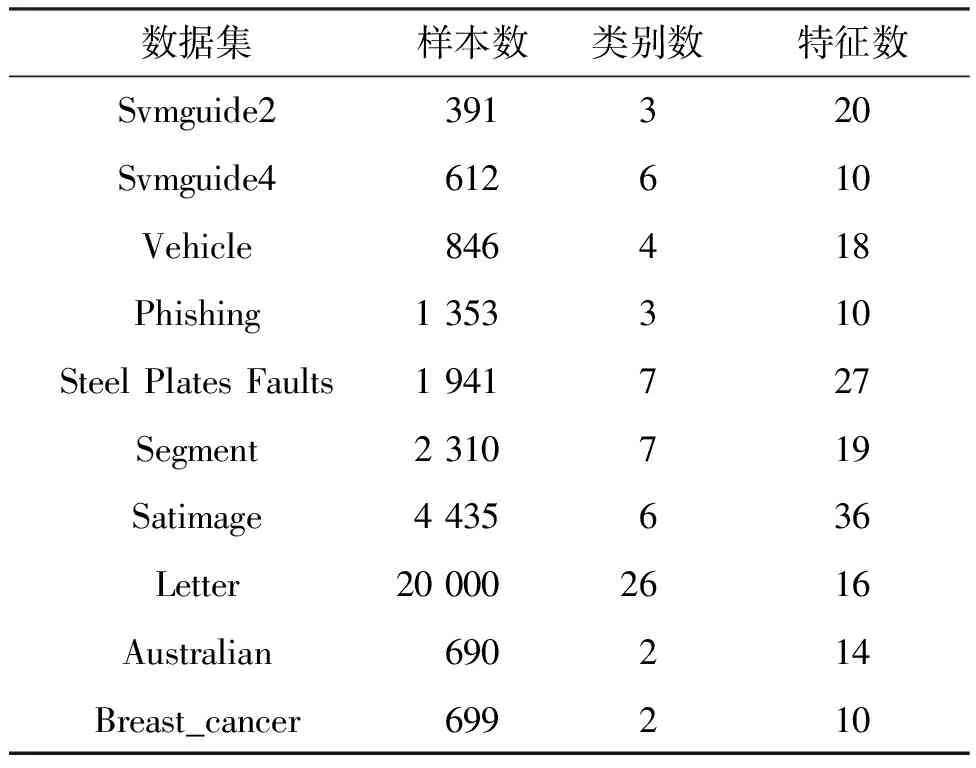
表1 实验数据集

2.1 实验设计

使用的数据集均为UCI数据集，参照文献[16]中所示方法模拟生成众包数据。首先为每位标记者随机生成标记准确率t，t∈(0.3,0.9)；再根据每位标记者的准确率对原数据集随机抽样，样本数据按照准确率t被赋予正确标签，其他数据均被随机赋予错误标签，由此生成标签数据集。实验为每个数据集生成了标记者数分别为1～10的标签数据集，为保证实验结果可信，每次的标签生成过程重复5次。

考虑数据分布的多样性，实验中采用的是经典的噪声环境下基于密度的聚类(density-based spatial clustering of applications with noise，DBSCAN)算法。DBSCAN算法包含3个参数，分别是X、ε、mp。其中：X为数据集的特征；ε表示样本间的最小距离，即若两样本间距离小于ε，则样本互为邻域；mp表示形成簇类所需的最小样本个数，将mp设定为特征数的2倍。ε和mp的计算方法分别为：

ε=d(0.005l(d))

(6)

mp=2dx

(7)

其中，d表示排序后的数据特征的距离向量，ε为该向量千分之五处的值，l(·)表示计算向量长度的函数，dx表示数据集的特征数。

2.2 实验结果分析

为验证本文算法的有效性，从时间效率及标签推测准确性两方面考虑方法效率。时间效率为各个算法在每个数据集上的5次实验的平均运行时间，标签准确率如式(8)所示。

(8)

2.2.1 不同标签数对准确率的影响

图3所示为5种算法在10个数据集上实例被标记次数为2～10的准确率。由图3可知，5种方法的实验准确率均随标签数的增多而提高。标签数为1时的实验结果参考性不大，因此图中未表示出来。在标签数为2时，MV算法与GLAD算法的实验效果均较差，DS算法的表现也差强人意。在大部分数据集上，当标签数多于2时，各个算法的准确率均随着标签数的增多快速提升，当每个实例的标签数多于7时，各个算法的准确率均趋于1，效果相差较小，且几乎不再随着标签数的增多而有所提高。

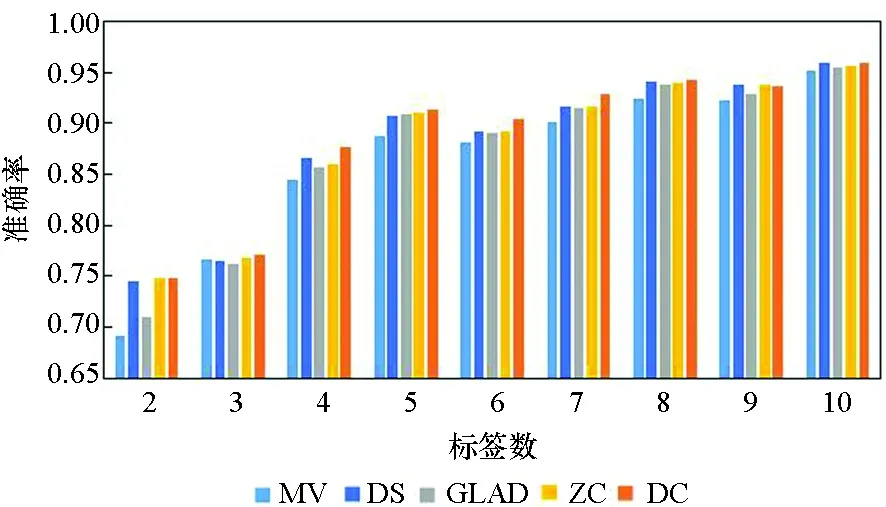
(a) Svmguide2

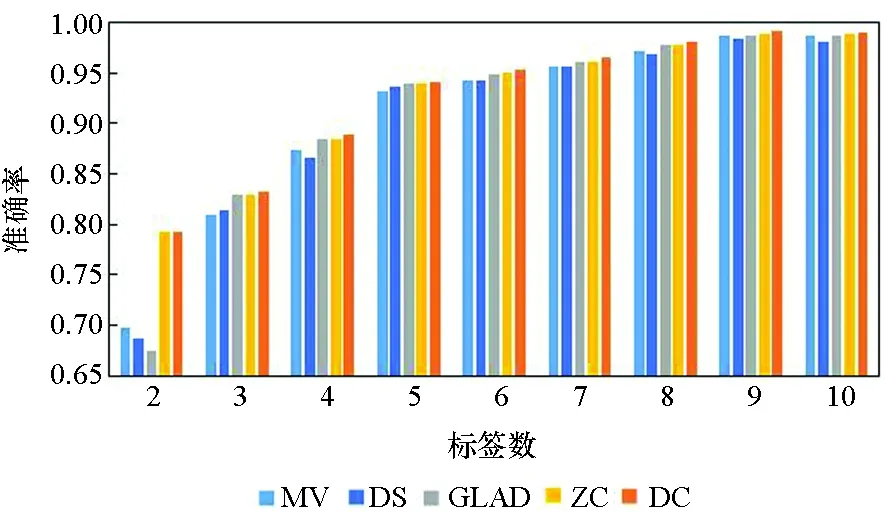
(b) Svmguide4

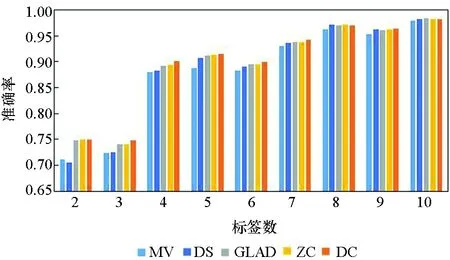
(c) Vehicle

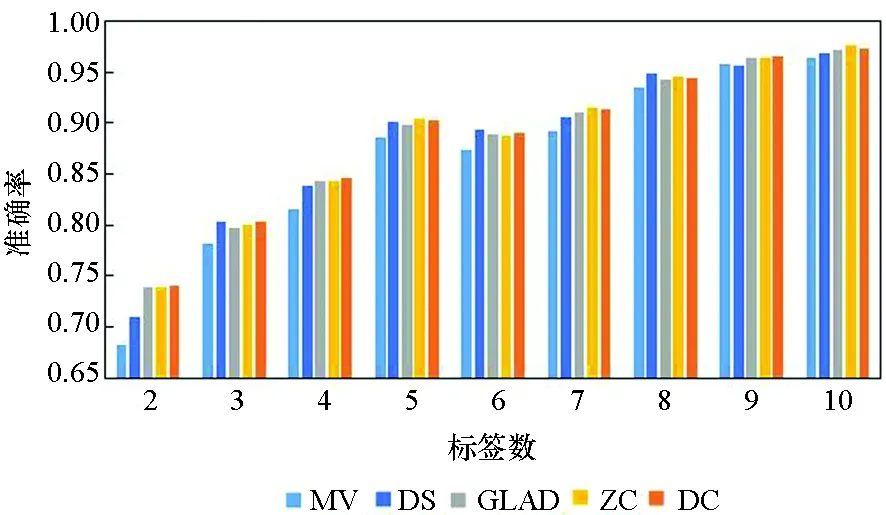
(d) Phishing

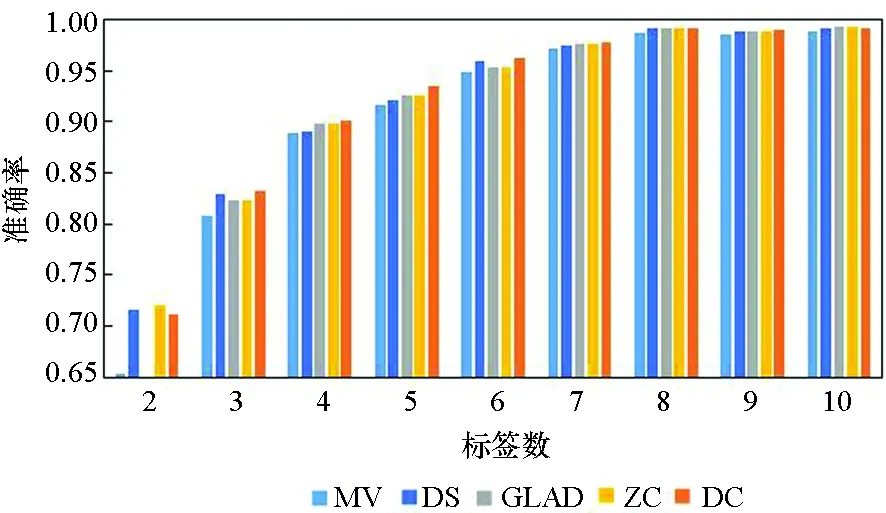
(e) Steel Plates Faults

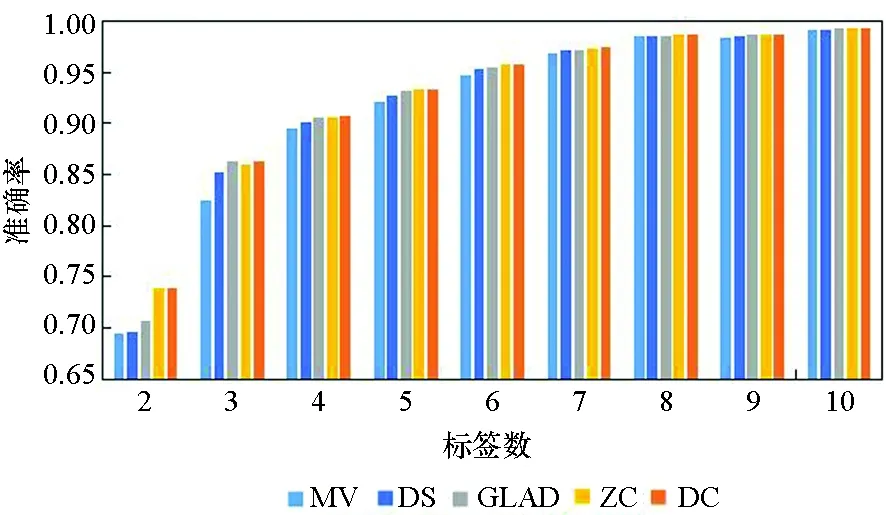
(f) Segment

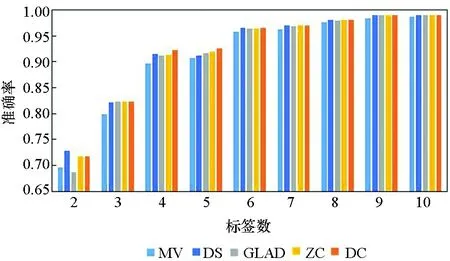
(g) Satimage

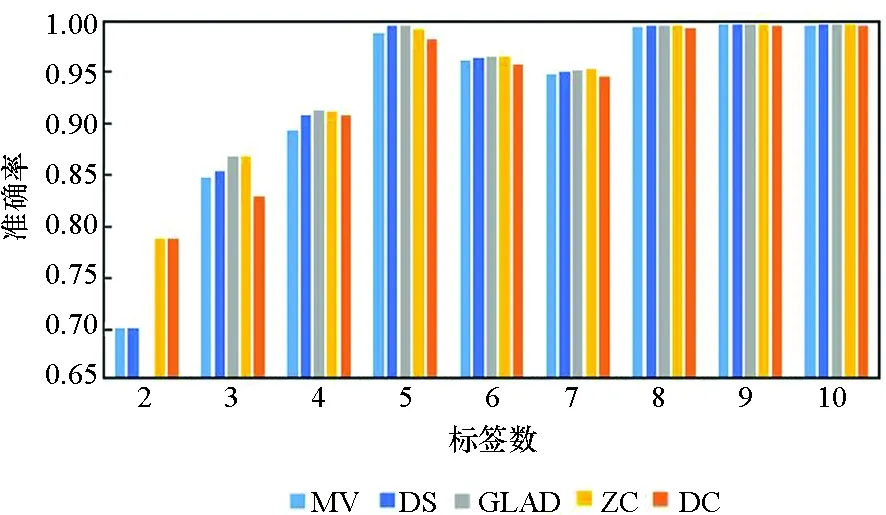
(h) Letter

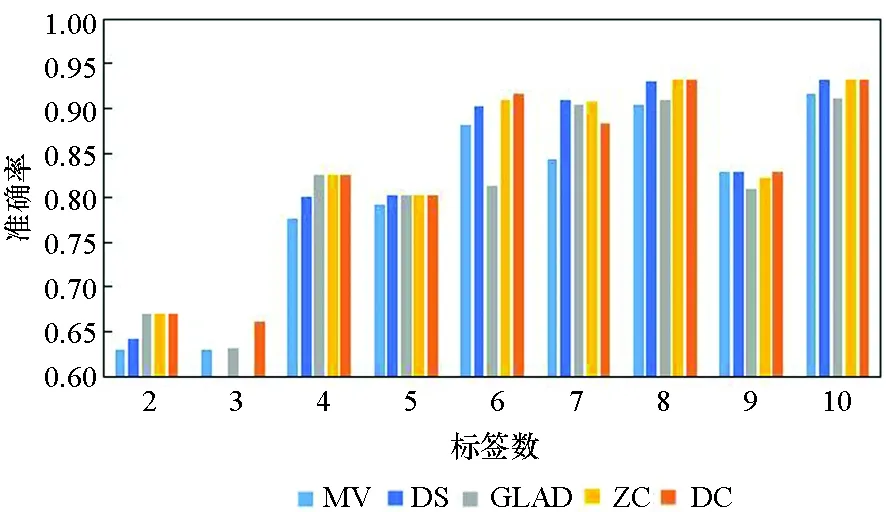
(i) Australian

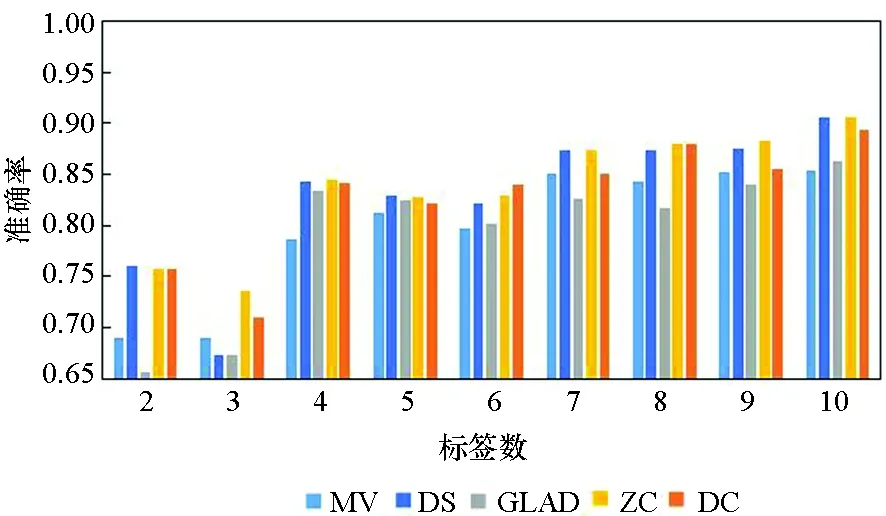
(j) Breast_cancer 图3 不同标记者数目在各数据集下的算法准确率Fig. 3 Accuracy of the algorithm for the number of different markers in each data set

在真实众包数据中，每个样本的标签数均大于7的可能性较小，因此主要分析标签数为4～7的实验结果。显而易见，在大部分数据集上，当标签数为4～7时，DC算法的实验效果略优于其他4种算法，其他情况时与另外4种算法的实验效果相近，而在实际的标注中，得到的标签数据往往没有很多，因此DC算法相较其他方法有一定优势。DS算法及ZC算法在二分类问题中的实验效果比MV、GLAD、DC算法好，而在多分类问题中GLAD、DC算法的效果较其在二分类中的效果有明显的提升。

图4给出了各算法在标签数分别为4～7时准确率的临界差异(critical difference，CD)图。CD图是基于统计显著性差异的算法对比模式，可以给出不同算法的排名。图4中算法排名越小表示算法效果越好。在标签数为4～7时，DC算法准确率均高于其他4种算法。图中算法的平均排名基于10个数据集和10种标签数量。

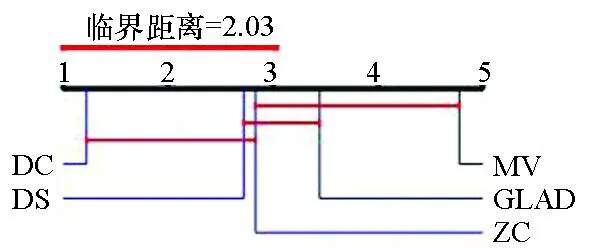
(a) 标签数为4(a) Number of labels is 4

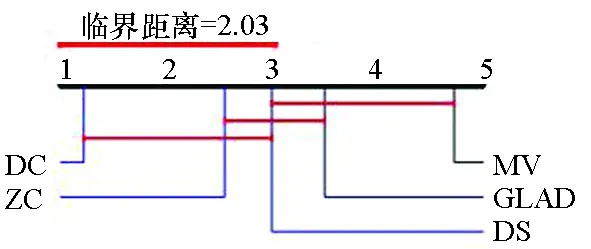
(b) 标签数为5(b) Number of labels is 5

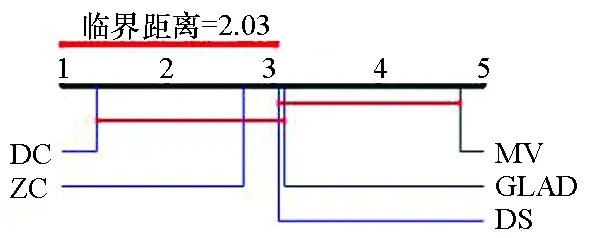
(c) 标签数为6(c) Number of labels is 6

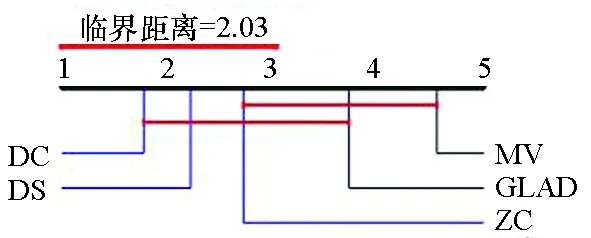
(d) 标签数为7(d) Number of labels is 7图4 临界差异图Fig. 4 Critical difference diagram

2.2.2 与其他算法的比较分析

表2所示为5种方法分别在标签数为1～10时的实验数据均值的比较。由表2所示可知，DC算法在8个数据集上的表现最优，相比最差的实验数据分别提高了1.9%、2.23%、1.52%、2.14%、1.62%、1.45%、3.86%、5.39%；相比其他4种算法平均提高了1.12%、1.52%、0.65%、1.11%、1.06%、0.72%、1.68%、2.26%。在Segment和Satimage数据集上的表现也仅次于最好的算法结果，且分别相差1.03%、0.79%。这是由于数据集的类别数增多，噪音分散严重。

在各个数据集中，由于标记者的准确率随机给出，且绝大部分标记者的准确率高于0.5，因此MV算法的准确率随着标签数的增多而提高，而在真实数据集中，标记者的准确率并没有随机给出的准确率高，导致MV算法的准确率其实并没有实验所示的那么高。又因为标签数据中的噪音是根据给定的标记者的准确率随机给出，所以多分类噪音没有二分类问题中的噪音结果集中，而是被分散到了所有可能的标签上，这样就导致MV算法在多分类问题中的准确率更高，其他4种算法也受此影响。

当标记者准确率较低时，GLAD算法相较其他算法在各个数据集中的实验效果较优，但该算法的迭代时间相较其他算法过长；DS算法使用的基本算法是EM算法，其实验效果受初值影响较大，DC算法结果为运行效果最好的结果；ZC算法在各数据集上的表现相对MV、DS、GLAD算法是最好的。DC算法在大部分数据集上的实验效果相较其他4种算法均为最优的。

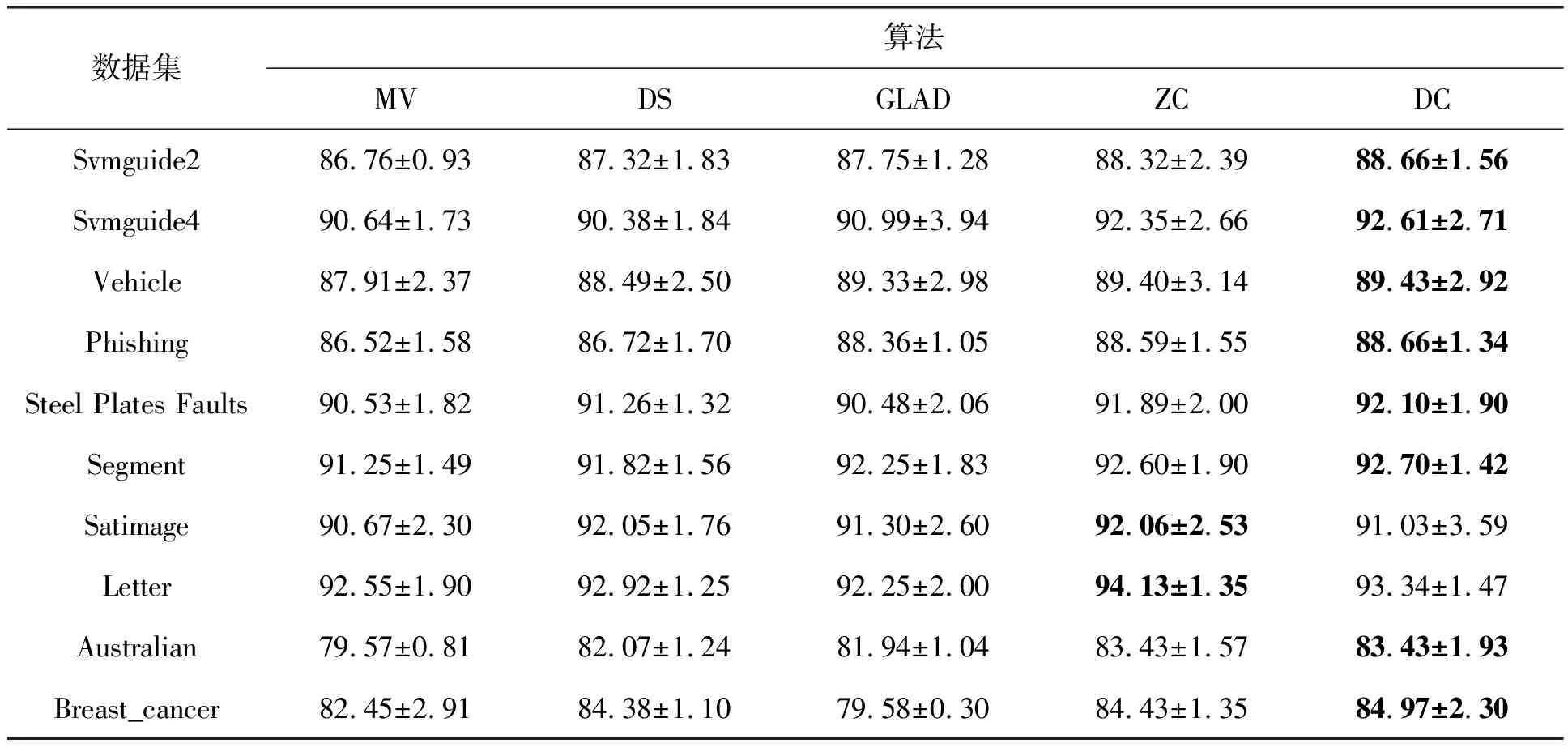
表2 各算法在各数据集中的平均准确率

图5为5种算法在10个数据集上的平均运行时间，由于GLAD算法的运行时间相较其他4种算法长很多，因此图中所示的GLAD算法的运行时间为真实运行时间的1%。5种算法的运行时间均随数据集数目的增大而变长，其中：MV算法的运行时间最短；ZC算法与DS算法耗时相近；DC算法实验过程中要运行聚类算法，因此耗时较DS、ZC、MV算法略长。

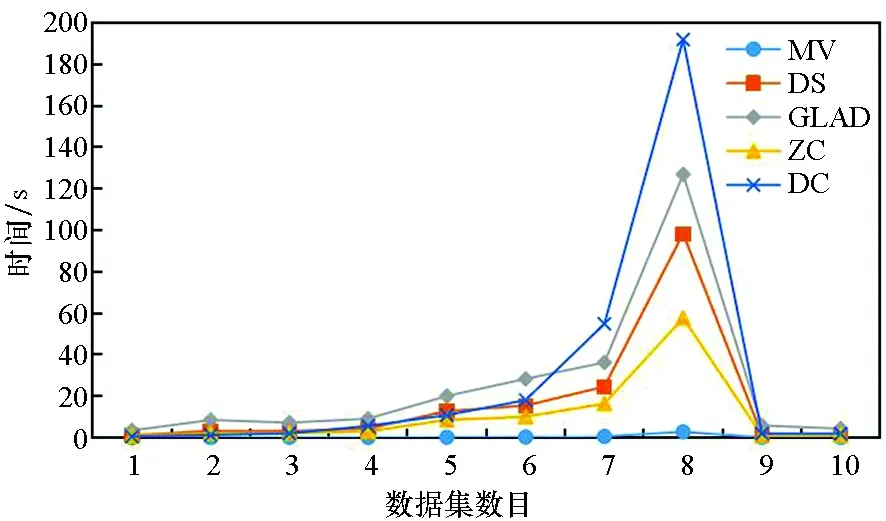
图5 算法运行时间Fig.5 Running time of algorithms

3 结论

本文考虑了数据分布和标签信息两方面的置信度，首先根据DBSCAN聚类算法将样本数据聚类，由此结果得到标记者置信度的第一部分，再由标记者相似性计算得到置信度的第二部分，最后根据标记者置信度推断实例的真实标签。实验结果表明，DC算法在标签数处于3～7的情况时，效果优于其他算法。

由于DC算法使用了聚类方法，考虑到聚类结果的准确性可能对实验结果有一定影响，因此未来工作将针对聚类算法对实验结果的影响以及纠正聚类结果的准确性这两部分展开，以提高标签推断算法的准确性。