基于非平稳时间序列分析的发动机订单预测模型
谭祖健 官丹萍 莫 愁 丁振伟 李晓霞
(1.广西玉柴机器股份有限公司,广西 玉林 537005;2.桂林电子科技大学,广西 桂林 541004)
0 前言
基于已有产品销售数据预测将来的订单变化趋势,进而配备合适的生产所需零部件库存,并制定合适的生产方案,能够在很大程度上提高订单快速交付的能力。对于如何准确地预测产品订单,众多研究者均取得过较好成果。杜莹利用平滑指数模型优化了某汽车公司的订单预测方法,并改善了该公司生产经营流程中的重复环节,降低了库存量,提高了效益。佟晶博将动态神经网络算法引入订单预测模型中,建立了河蟹电商分销系统,该系统能够预测未来一段时间内各分销商的订单。李浩等人构建了一种融合VGG 网络与全卷积网络(FCN)的出租车多区域订单预测模型,与基于BP 神经网络、RBF 神经网络的预测模型相比,该预测模型平均准确率更高且均方根误差更低。也有一些研究的目标并非提出成套的预测方法,而是着眼于提升预测过程中某个环节的质量和/或简便程度。例如DANIEL ORTIZ-ARROYO 等人在模糊逻辑预测模型中,将有序加权平均算子应用于原始时间序列划分并重构,使一阶预测模型精度比对比文献高,尽管该模型精度仍达不到高阶模型的水平,但仍然可以缩短计算时间。刘道元等人为了准确预测某批订单的剩余完工时间(以便动态调整生产计划、优化制造过程),提出了一种基于自组织映射(SOM)网络-特征加权模糊C 均值(FWFCM)的特征选择算法。在现有的公开文献中,直接针对发动机订单预测进行研究的文献数量较少。
1 模型选择及模型特性分析
1.1 发动机订单序列特性分析与模型选择
根据时间先后顺序将一定时间范围内的采样数排列成1组或多组数列,这些时间序列可以表征某种特征变量随着时间不断变化的过程和趋势。发动机月订单数量、季度订单数量就是一种典型的时间序列。但该时间序列在1 a 周期内的每个月、每个季度都不是固定在某个范围内的,而是随着企业产品质量、企业供货能力、客户需求以及社会宏观经济环境好坏等因素的变化呈一定规律的非平稳变化,而且这个变化是隐含的,需要进一步挖掘才能用一定的模型来表征。由于非平稳时间序列特征数据呈随机变化的趋势,其数理统计性质也会随着时间推移而发生变化,因此对这种特性的数据进行未来趋势预测时,必须选择能评估和处理序列中随机扰动项、能处理数理统计性质变化的模型。满足这个要求的模型有自回归条件异方差模型(ARCH 模型(Autoregressive Conditional Heteroskedasticity Model))、灰色模型和自回归整合滑动平均模型(ARIMA 模型)等。其中,ARIMA 模型在建模时考虑了时间序列的自回归特性和滑动平均特性,并进行了平稳化处理,因此比较适合分析发动机订单时间序列和预测未来订单。
1.2 模型特征分析
自回归功能可以描述一组变量在前后期的变化特征,即用前期若干时刻的随机变量的线性组合来表征后期某时段随机变量的线性回归。其与用自变量预测因变量的其他线性回归不同,该功能是用前期的预测后期的(自身)。将该自回归模型记为(),将随机序列记为X,其模型结构如公式(1)所示。

式中:为时间点;为模型阶数;,,…,a为自回归系数(当=0 时,()去中心化);{}为白噪声序列。
对时间点来说,如果有∀ <,(Xε)=0,即如果任意小于时间点的时间点对应的变量与白噪声序列相乘,其数学期望均为0,则表明前面的时间序列与后面的白噪声不相关,这是ARIMA 模型自回归功能的基本条件和优点。
对发动机订单时间序列的非平稳性特征来说,线性回归模型等简单模型的精度较低。自回归模型将尽量消除白噪声影响作为建模目标,因此它可以获得较高的精度。
对公式(1)来说,只有确定了系数a,其才有使用意义,否则公式(1)就是一个无穷多项式。可以用白噪声序列ε,ε,ε,…,ε表示随机序列X,并将滑动平均模型记为MA(),其模型结构如公式(2)所示。
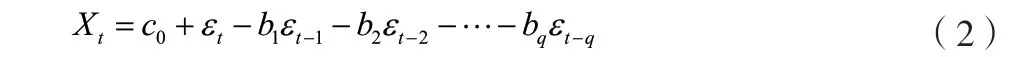
式中:为多项式常数,由变量特征确定;为模型阶数;,,…,b为滑动平均系数,且|b|<1,此处=1,2,…,。
如果设定了b的范围,则公式(2)是收敛的。=1 的特例MA(1)如公式(3)所示。

由公式(3)可知,X为2 个扰动因子(白噪声)ε和ε的加权平均。根据以上分析可知,MA()模型是AR()模型的模型阶数受到某种限制时的情形。由于ARIMA 模型融合了AR()模型和MA()模型,且值和值的大小体现了这 2 个模型在 ARIMA 模型中作用的强弱,因此在应用时需要确定值和值。
由于类似发动机订单这样的时间序列有明显的趋势性和/或季节性,因此在建立ARIMA 模型时需要先去除这2 个趋势,再进行平稳化处理。一般来说,进行1 次差分和2 次差分就可以剔除其中1 个趋势和2 个趋势。
1.3 ARIMA建模程序
使用ARIMA 模型进行订单预测的一般步骤如下:首先,对样本进行平稳性检验,如果不平稳,通常就进行若干次差分,直到样本平稳。其次,对模型进行定阶,确定ARIMA(,,)(为为检验样本平稳性而进行差分的次数)中和值后即可建立模型。再次,对模型进行适应性检验,达到误差要求后才可用于预测未来变量,否则需要重新进行平稳化处理或重新确定阶数。ARIMA 建模和预测流程如图1 所示。
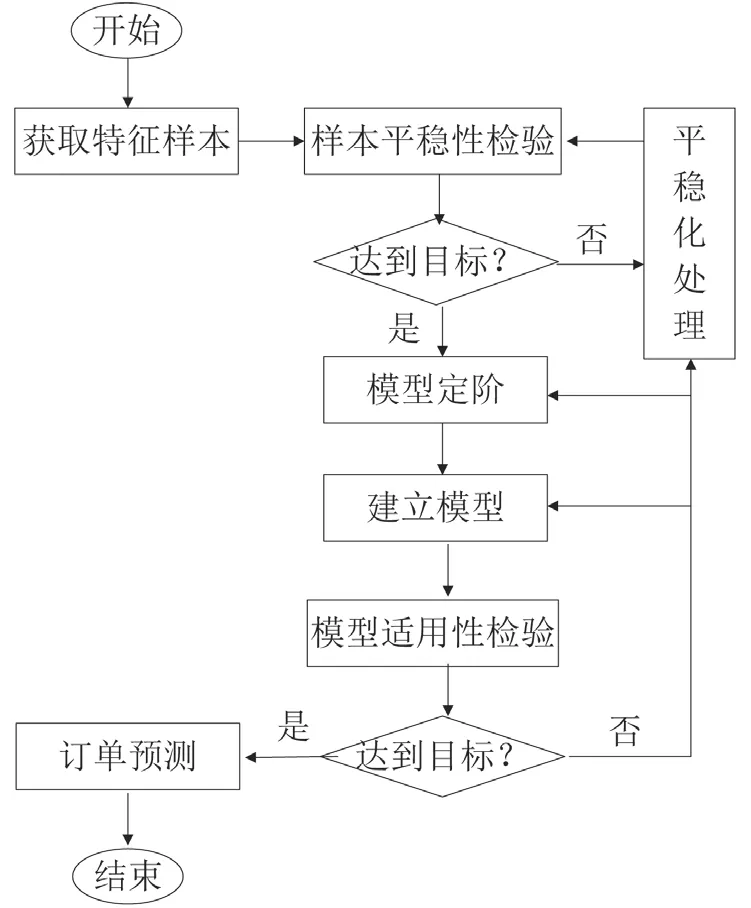
图1 ARIMA 预测建模流程
平稳性检验可以判断特征样本隐含的是确定性趋势还是随机趋势(或者二者兼有)。主要方法有以检验单位根为手段的笛基-福勒检验(Dickey-Fuller 检验)和以检验误差项自相关或异方差为手段的菲利普斯-佩隆检验(Phillips-Perron 检验)。在对模型进行定阶时,确定值和值的方法主要有自相关函数法、偏自相关函数法、赤池信息准则(Akaike Information Criterion,AIC 准则)法和贝叶斯信息准则(Bayesian Information Criterion,BIC 准则)法;模型适应性检检验的目的是评估建立的模型时间序列与样本时间序列的相关性,评价手段是检验拟合残差项{ε}是否为白噪声。建立的模型建立的模型如果显著有效,则表现为提取样本中全部或接近全部相关信息后,残差没有相关性,即{ε}应为白噪声。通常会通过杨-博克斯Q 统计量检验(Ljung-Box Q Test,LBQ 检验)来评估模型是否显著有效。
2 实例应用及分析
以某发动机生产商1995—2017 年(共23 a)每季度的发动机订单为样本,基于以上理论,使用MATLAB 软件编制相关程序,建立ARIMA(,,)模型,并预测未来3 a(2018—2020 年)的季度订单。
2.1 建立一般预测模型
通过Phillips-Perron 检验对样本进行平稳性检测的方法如下:首先,用最小二乘法估计样本回归模型,得到参数估计和残差序列。其次,利用残差自相关中的信息计算统计量Z,如果Z满足设定显著性水平的限值,则认为该样本平稳。在MATLAB 中调用pptest 函数进行Phillips-Perron 检验的程序语句为[h]=pptest(x,'model','AR')。其中,(输入参数)为检验的序列,该文为发动机订单序列;'model','AR'为检验的模型选用AR(自回归)模型;(即输出参数)为测试结果的布尔决策向量,当=1 时,表示拒绝有单位根的假设,当=0 时,表示不能接受原假设,即模型有单位根。
将实例样本发动机季度订单序列作为语句中的量代入,得到=0,则该实例样本不平稳。因为实例样本为季度订单,具有典型的季节性和趋势性,所以首先,应以=4 的步长做1 次差分去除季节性。其次,以=1 的步长再做1 次差分去除趋势性。最后,对差分后的时间序列进行同样的检验,检验结果表明,该序列平稳。
使用AIC 准则对模型定阶的基本原理是针对样本时间序列建立 ARIMA 模型,用极大似然方法估计模型参数,不同的AR 阶数(值)、MA 阶数(值)组合会得到不同的残差、方差的极大似然值,最小极大似然值对应的阶次即为最优值、值。在该实例使用AIC 准则时,根据经验确定最高阶次为4,在MATLAB 软件中运行AIC 准则程序得到的AIC 定阶数值分布热度图如图2 所示。图2 中的数值均为热度值,深浅不同的颜色表示不同热度。由图2 可知,有2 组阶数组合的最小极大似然值为1.641,取阶数较小者,得到最佳自回归阶数()=3,滑动平均阶数()=3。
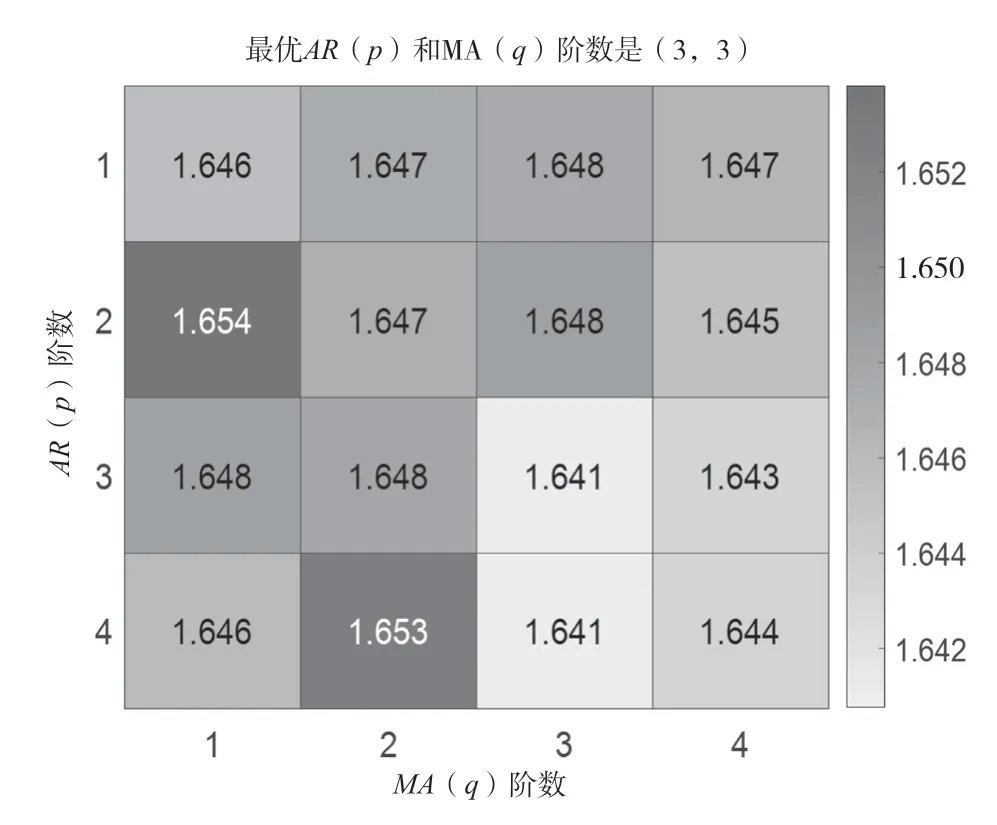
图2 一般预测模型AIC 定阶数值分布热度图
根据样本平稳化处理时所做的差分次数以及使用AIC法则定阶时的()阶数、()阶数,可建立模型ARIMA(3,2,3)。然后用LBQ 检验来评估模型是否显著有效。在MATLAB 中调用 lbqtest 函数进行检验的程序语句为[h]=lbqtest(reg,'Lags',1:4,'alpha',0.05)。其中,(输入变量)为用于检验的残差序列;(输入变量)为检验的滞后项数目,这里分别取1、2、3 和4 共4 个项数;(输入变量)为假设检验的显著性水平,这里取0.05;(输出变量)为检验结果,因为滞后项数目是4,所以这里的测试次数为4 次。在每次得出的结果中,如果=1,则表示拒绝残差无自相关的零假设,如果=0,则表示不拒绝残差无自相关的零假设,即说明残差没有自相关性。该模型的检验结果显示4 个项数均有=0,可知建立的模型显著有效。
2.2 未来订单预测及分析
基于第2.1.3 节建立的模型,可预测2018—2020 年的季度订单数量。在MATLAB 软件中调用forecast 函数预测未来订单的程序语句为[Y,YMSE]=forecast(mdl,12,'Y0',x)。其中,mdl(输入变量)为建立的ARIMA 模型,即预测的推理依据;12(输入变量)为预测范围,即预测未来12 个季度的订单;'Y0',意为前样本响应数据为,即数据初值为发动机订单序列;(输出变量)为预测值,为的均值平方误差。
运行此程序得到的结果如图3 所示(”预测订单1“部分)。为了分析预测订单趋势和以往实际发动机订单的变化趋势,该文将1995—2017 年发动机季度销量绘制在同一图中(即图3“实际订单”部分)。由图3 可知,与实际订单变化情况一样,2018—2020 年的预测订单逐年上升,且每年内4 个季度的订单也逐季上升,呈现明显的季节性。实际订单与预测订单的曲线变化趋势的一致性较好。
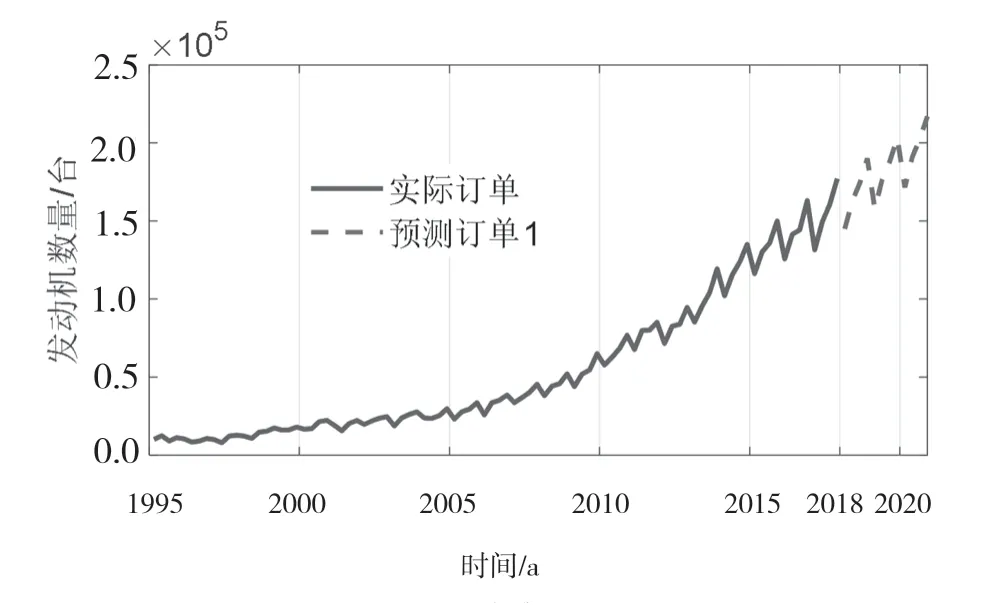
图3 发动机实际订单与预测订单曲线
2.3 季节性预测与一般预测模型建模效果的比较分析
第2.1 节和第2.2 节是根据ARIMA 模型的一般流程来建模并分析的,而文献[6]给出了一种在MATLAB 中直接利用arima 函数中的“Seasonality”来建立季节性模型的方法。与传统方法相比,这种方法更简洁,因为其保留了样本的季节性,所以建模时只需要进行一次差分去除趋势性即可。这种建模方法需要配合使用AIC 准则来判断最优的()阶数和()阶数,方法同第2.1.2 节所述。在MATLAB 中调用ARIMA 函数建立模型的程序语句为model=arima('D',1,'Sea sonality',4,'SARLags',i,'SMALags',j)。
语句含义为根据括号内设置的参数建立一个ARIMA 模型。其中,'D',1 意为差分次数是1;'Seasonality',4 意为季节差分滞后算子多项式程度是4;'SARLags',i,'SMALags',j 意为()阶数和()阶数分别为由AIC 准则确定的最优的值和值。
基于一阶差分样本得到的AIC 定阶数值分布热度如图4所示。由图4 可知,各组()和()组合对应的极大似然值与样本经过2 次差分后得到的结果不同,最佳()=4,()=1,因此可建立模型ARIMA(4,1,1),并用LBQ 检验模型残差,由检验结果可知,该模型显著有效。用该模型预测的2018—2020 年季度订单数量如图5 所示(“预测订单 2”部分)。
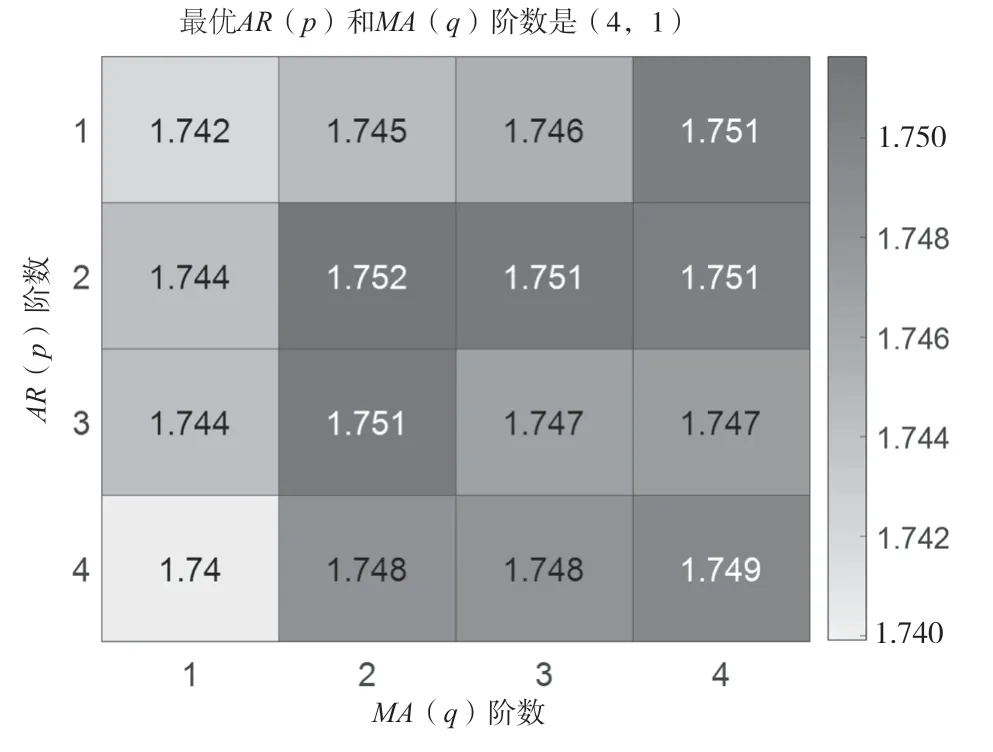
图4 季节性预测模型AIC 定阶数值分布热度图
为分析模型可信度,该文将2018—2020 年实际的发动机季度订单与2 种建模方法所得的预测订单进行比较,绘制的变化曲线图如图5 所示。由图5 可知,2 种方法所得的预测订单都很好地跟随了实际订单的变化,且除2020 年第一季度外,季节性预测模型所得预测订单均更接近实际订单的变化。2 种方法所得的2020 年第一季度预测订单与实际订单的相对误差分别为6.2%和9.3%,而其他季度的相对误差均为0.9%~2.3%,误差较小。整体分析预测值与实际值的相关性,在显著性水平=0.05 的情况下,2 种模型的预测结果均有决定系数=0.89,在满意范围内。

图5 2018—2020 年预测订单与实际订单的比较
时间序列预测基于这样一个假设:预测期与样本采样期的环境条件基本相同。而2020 年第一季度由于受新冠疫情影响,国内外生产经营环境严重恶化,样本采样公司当季销量同比增幅极小,而当季的预测值与实际值较大误差为9.3%。
3 结论
为了满足快速交付订单的客户需求,首先,该文研究了某公司1995—2017 年(共23 a)的发动机销量时间特性,选择ARIMA 模型建立发动机订单预测模型。其次,分析了ARIMA模型适用于非平稳时间序列分析的自回归功能、滑动平均功能和平稳化处理特征,给出了订单预测模型的建模步骤。再次,以某公司以往订单为训练样本,使用该模型预测了2018—2020 年3 a 的季度订单,结果表明,预测订单的变化曲线与以往实际销售数量的变化曲线的一致性较好。从次,将2018—2020 年的预测订单与实际订单进行比较,结果显示两者误差较小,决定系数较高。最后,得出该文所建立的预测模型具有较高的可信度,可以对发动机订单进行预测。

