完全0-单半群上的共轭关系*

刘鑫， 陈辉， 王守峰

(云南师范大学 数学学院，云南 昆明 650500)

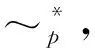
1 基本定义及引理

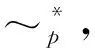
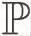
其中,当a≠0时,

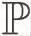
a～trb⟺(∃ɡ,h∈S1)ɡhɡ=ɡ,hɡh=h,ɡaw+1h=bw+1,hɡ=aw,ɡh=bw.

由文献[7]中的定理4.5,有以下结果:

引理1[7]设S是群界半群,a,b∈S.则a～trb当且仅当存在ɡ,h∈S1使得

aɡ=ɡb,bh=ha,ɡh=aw,hɡ=bw.

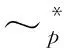
a～nb⟺(∃ɡ,h∈S1)aɡ=ɡb,bh=ha,haɡ=b,ɡbh=a,

并指出这是一个等价关系.

众所周知,完全0-单半群是一类重要的半群.1940年，Rees给出了这类半群的如下结构.

引理2[9]设G是群,I,Λ是非空集,P=(pλi)Λ×I是矩阵,pλi∈G0且P满足正则条件

(∀i∈I)(∃λ∈Λ)pλi≠0;(∀λ∈Λ)(∃i∈I)pλi≠0.

在S=(I×G×Λ)∪{0}上定义运算

则S是完全0-单半群.记S=M0[G;I,Λ;P].反之,任意完全0-单半群均可如此构造.

据文献[9]的定理3.2.11及其证明，有下面的引理.

完全0-单的逆半群称为Brandt半群.文献[9]的定理5.1.8给出了Brandt半群的如下结构:

引理4[9]Brandt半群是且仅是M0[G;I,I;Δ]，其中Δ=[δij]为I×I矩阵且

e是G中的单位元.

对完全0-单半群上的共轭关系,据文献[7]中的定理4.8,命题4.26及文献[8]中的命题2.3,有以下结果.

2 主要结果

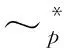
引理6设

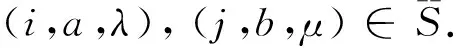
则以下陈述等价:

(1) (i,a,λ)～n(j,b,μ);

(2)(i,a,λ)～c(j,b,μ);

(3) (i,a,λ)～p(j,b,μ);

(5) (i,a,λ)～tr(j,b,μ);

(6) (∃c∈G)b=(cpμj)-1apλic.

证明由引理5,只需证明(5)蕴含(6)和(6)蕴含(1).

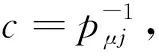
(i,a,λ)(k,c,v)=(k,c,v)(j,b,μ),(j,b,μ)(s,d,w)=(s,d,w)(i,a,λ),

由上述等式知

pvs≠0,pwk≠0,w=λ,v=μ,k=i,s=j,apλkc=cpvjb.

整理后可得b=(cpμj)-1apλic.

(i,a,λ)(i,c,μ)=(i,apλic,μ)=(i,cpμjb,μ)=(i,c,μ)(j,b,μ)，

类似可证

故(i,a,λ)～n(j,b,μ).

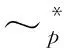
定理1在完全0-单半群S中，以下陈述成立:

(1)[0]n=[0]c={0}.

(2)若(i,a,λ)∈S且pλi=0，则[(i,a,λ)]n=[(i,a,λ)]c={(i,a,λ)}.

(3)若(i,a,λ)∈S且pλi≠0，则

证明(1) 由～n和～c的定义立得.

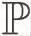
(i,a,λ)(k,c,v)=(k,c,v)(j,b,μ)，(j,b,μ)(s,d,w)=(s,d,w)(i,a,λ).

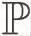
(3)由引理6可得.

由引理4和定理1可得以下结果.

推论1设S=M0[G;I,I;Δ]是Brandt半群.则以下陈述成立:

(1) [0]n=[0]c={0}.

(2)当i≠λ时，[(i,a,λ)]n=[(i,a,λ)]c={(i,a,λ)}.

(3)对(i,a,i)∈S,[(i,a,i)]n=[(i,a,i)]c={(j,b,j)∈S|(∃c∈G)b=c-1ac}.

特别地,当S有限时,若|I|=m,|G|=t且G有r个共轭类,则S有1+t(m2-m)+r个～n-类和～c-类.

下面考察S上的～p*-类和～tr-类.

定理2在完全0-单半群S中,以下陈述成立:

(1)[0]p*=[0]tr={0}∪{(i,a,λ)|pλi=0}.

(2)若(i,a,λ)∈S且pλi≠0，则

证明(1)设(i,a,λ)∈S.若(i,a,λ)～tr0，则由引理1知存在(j,b,μ),(k,c,v)∈S使得

(i,a,λ)(j,b,μ)=(j,b,μ)0=0,(j,b,μ)(k,c,v)=(i,a,λ)w.

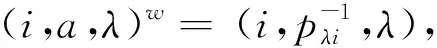
0(i,a,λ)=(i,a,λ)0=(i,a,λ)(i,a,λ)=0=0w=(i,a,λ)w.

由引理1知(i,a,λ)～tr0.故[0]tr={0}∪{(i,a,λ)|pλi=0}.设(i,a,λ)∈S，pλi=0.由矩阵P的正则条件知存在j∈I使得pλj≠0.于是

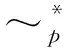
[0]p*=[0]tr={0}∪{(i,a,λ)|pλi=0}.

(2) 由引理6可得.

由引理4和定理2可得下面的结果.

推论2设S=M0[G;I,I;Δ]是Brandt半群.则以下陈述成立

(1) [0]p*=[0]tr={0}∪{(i,a,λ)|i≠λ}.

(2)对(i,a,i)∈S，则[(i,a,i)]p*=[(i,a,i)]tr={(j,b,j)∈S|(∃c∈G)b=c-1ac}.

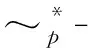
由定理1和定理2可得下述结果.