基于Hough 变换及卷积神经网络的工程图图线识别技术及应用研究

石林坤，田怀文，蒲虹林

（西南交通大学 可视化研究中心，四川 成都 610031）

工程类图纸识别一直是工程领域研究的热点，其广泛应用于电气工程、机械工程等不同行业。林铭德等人[1]利用对图纸的识别，自动获取图纸中电气构件数据。唐虹等人[2]通过对汽车线束图纸的识别，达到了线束分类识别的目的。YANG 等人[3]提出了一种从工程图纸生成语义丰富的结构模型的半自动方法。文献[4]利用AutoCAD 软件读取考生答案中的图元，进行试卷的批改。直线和曲线是工程图纸中重要的几何元素，对直线和曲线的自动识别研究是实现图纸完整、快速识别的关键技术。因此，有效的直线和曲线检测方法对工程领域研究具有重要意义。LIU 等人[5]提出了一种基于锚点的Hough 变换，其在检测较为简单的工程图图纸的直线中有较好的效果，但用于检测较为复杂的工程图图纸时，仍需较大改进。CUNEYT 等人[6]采用最小二乘法对锚点形成的边缘映射进行直线拟合，但仍存在少量虚假直线。马俊俊[7]提出了基于种子段的动态步长直线矢量化算法，通过跟踪种子段进行直线识别，但其检测结果容易受到直线连续性的影响。刘璧钺等人[8]提出了一种基于LSD 算法的直线检测。ALlWAN 等人[9]提出了一种基于遗传算法的工程图元检测，该方法能够较为准确地提取工程图中的圆弧和直线，但对于图元重叠部分其提取效果较差。SALMON 等人[10]提出了一种从曲率剖面中检测圆弧和线段的方法。文献[11]提出一种基于教与学的优化算法和梯度分析实现对图像的圆检测。文献[12]提出了一种基于模拟退火和差分演化的自动圆检测算法，该算法能够较为准确地检测图像中的圆，但其对噪声较为敏感。

本文针对工程图图线语义较为丰富、实际情况较为复杂等问题提出了一种基于Hough 变换的工程图图线识别技术。如图1 所示，基于Hough 变换的工程图图线识别具体步骤：（1）对采集的工程图进行预处理；（2）利用Hough 变换、RANSAC 算法、最小二乘法检测图像中的直线；（3）利用形态学开闭运算及漫水填充算法检测并分离曲线；（4）利用卷积神经网络对各图线ROI进行图线线型分类，得出线型关系。

图1 图线识别算法流程图

最后结合工程制图类课程试卷自动评阅需求，在识别算法的基础上增加坐标转换算法及曲线一致性判断，对30 名学生的工程图图纸考卷进行评分，并与人工评分结果进行对比，其评分差距在10%以内，表明该算法的可行性且在机械制图中有较好的应用价值。

1 工程图采集及预处理

为模拟真实工程图应用场景，本文通过扫描设备采集手绘图纸或打印图纸。实际采集过程中，因人为绘制习惯、设备误差等问题容易使采集的图像产生干扰，因此需要对图像进行预处理操作，其流程图如图2 所示。

图2 工程图预处理流程图

本文采用的图像预处理包括：（1）图像二值化，二值化可以极大地减少图像中的数据量，突显出目标轮廓；（2）HSV 空间转换，去除人为绘制误差产生的阴影干扰；（3）形态学膨胀，达到去除噪声的效果。其各步骤结果如图3 所示。预处理后的结果相较于采集图像，在保证原始工程图基本图元的情况下，大量减少了干扰点数量，且有更好的线条对比度，满足后续处理要求。

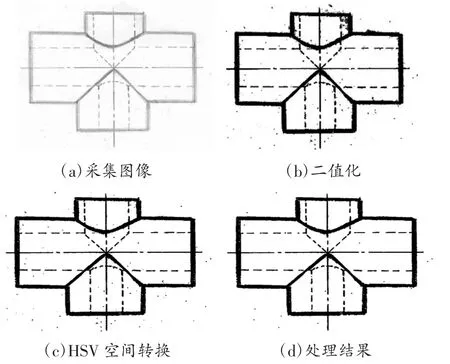
图3 工程图预处理过程结果

2 图线识别关键技术

2.1 Hough 变换直线检测

霍夫变换是由Paul Hough 于1962 年首次提出，仅仅用于图像中直线的检测。现在使用的广义霍夫变换不仅能检测直线，还可以检测其他形状的几何特征。由于Hough 变换检测直线是基于边缘特征提取，因此需要先对图像进行边缘检测。考虑原图像的分辨率是变化的，因此采用自适应阈值Canny 边缘检测算法[13]。如图4 所示，Hough 变换检测到的直线往往包含多段直线，导致其检测精度低，剔除这些多段直线对直线检测精度至关重要。在Hough 变换检测到的每条直线中，都有着对应的起点和终点。假定直线空间为XY 空间，点空间为KB 空间，XY 空间中的直线唯一对应的KB空间中的起点及终点。使用拟合算法剔除KB 空间中的“局外点”，从而对XY 空间进行直线去重。常用的拟合算法有最小二乘法和RANSAC 算法等。

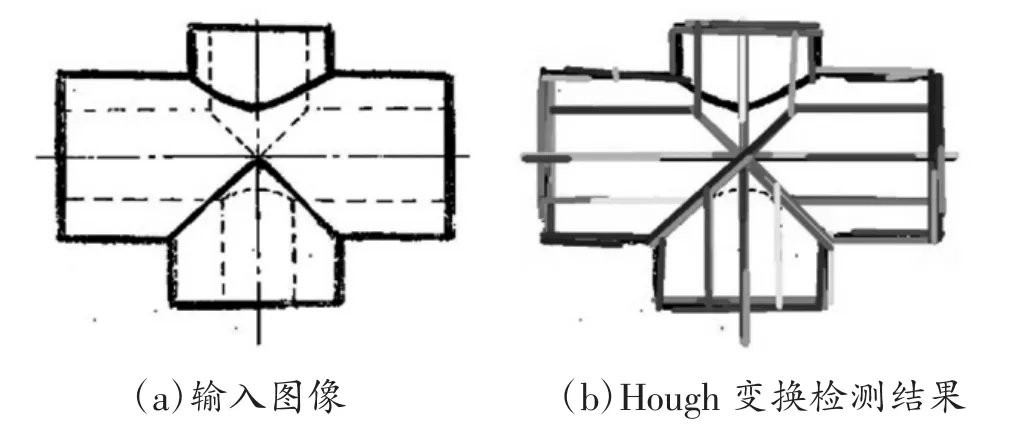
图4 Hough 变换处理结果图

2.2 基于RANSAC 算法的直线拟合

由图4 可知，通过Hough 变换检测出的直线对应的KB 空间存在部分“外点”，这些干扰点会直接影响直线的拟合精度。本文采用RANSAC 算法[14]对“局外点”剔除。RANSAC 算法是一种通过不断迭代，从一组数据中找出“局内点”，排除“局外点”，并通过“局内点”估计数学模型参数的算法。RANSAC 算法结果具有随机性[15]，检测不够精准。

最小二乘法是一种通过最小化理论值与观测值之间的误差平方和去寻找最佳匹配函数的算法，但由于最小二乘法会考虑所有样本点进行拟合，当存在“局外点”时，拟合结果较差。

二者区别主要在于，最小二乘法会尽量拟合所有点，RANSAC 算法排除“局外点”后，仅利用“局内点”计算模型。由于在空间中存在部分的“局外点”，若单独使用最小二乘法进行直线拟合，其拟合结果与理想情况会有较大误差，二者算法拟合结果对比图如图5 所示。

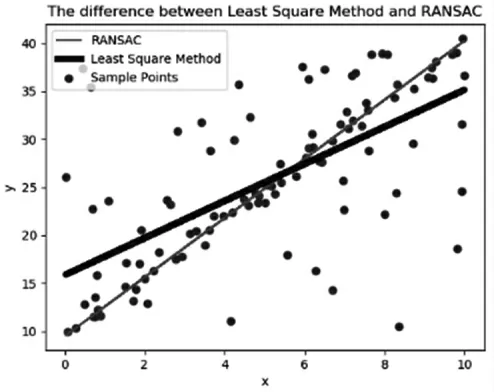
图5 RANSAC 算法和最小二乘法对比图

基于此，本文结合上述两种算法进行直线拟合。先随机地从测试集中选取一个子集进行参数估计，以此为基础估计参数化模型M，此时认为该子集中的点均为“局内点”。后用其余点测试该模型，如果某个点适用于该模型，即认为该点也是“局内点”，当有足够多的点被归类为“局内点”时，就证明估计的模型足够合理。扩充后的“局内点”重新估计模型，通过估计局内点与模型的错误率来评估模型，如果当前的模型错误率比之前最优的模型错误率低，即将当前模型置为最优模型，否则舍弃。重复一定的次数K 次后，有足够的样本点被归为“局内点”，得到最优模型M，假设需要“局内点”个数为n，置信度为P，θ 为n 个点适用于该模型的概率，则K 的计算公式如下：

通过不断地建立假设与检验的迭代，以期获得一组最优的“局内点”点集，再利用最小二乘法拟合“局内点”，得到拟合直线，其算法流程如图6 所示。

图6 直线拟合流程图

其检测结果如图7 所示，将应用上述算法直线检测结果图7 与Hough 变换检测结果图4（b）比较，可见该算法直线检测效果较好。

图7 直线拟合结果

2.3 曲线检测

在机械工程类图纸中，曲线常常包括圆、圆弧、一般曲线等。Hough 变换圆检测在检测圆方面有较好的检测效果，但对于圆弧及一般曲线的检测效果较差。若直接将原始图像和上述直线检测结果图7 进行布尔差运算，其结果如图8 所示。该结果中包含大量不易去除的干扰点，且单条曲线也被分离成多条曲线，这些误差会降低曲线检测精度。

图8 布尔差运算结果

对此本文采用形态学开闭运算进行曲线检测。形态学开闭运算是图像处理中常用的处理手段之一[16]，本文利用图像中的曲线特征，采用横向及纵向矩形结构元从图像中提取曲线边缘。使用该方法得到的曲线边缘为R3，其计算公式如下。

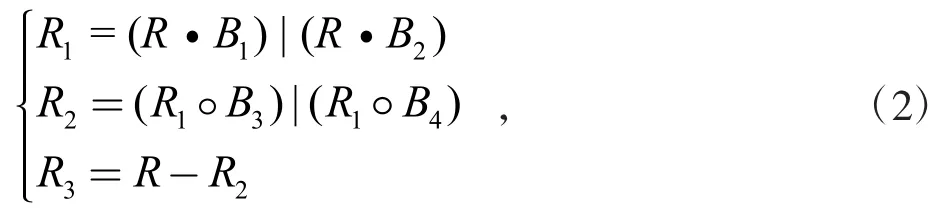
其中，R·B1表示B1对R 的开运算，R·B2表示B2对R的开运算，R1◦B3表示B3对R1的闭运算，R1◦B4表示B4对R1的闭运算，｜表示或运算，R 为原始图像，B1、B3是横向矩形结构元，B2、B4是纵向矩形结构元，其曲线检测结果如图9 所示。

当图像中存在多段曲线时，为实现后续图线线型识别，需要将多段曲线进行分离。本文采用漫水填充算法[17]对曲线进行分离。该算法适用于对内定义区域的填充。漫水填充算法能够将该区域中全部像素值设置为新值。通过一定规则确定一种子点，然后通过判断种子点的邻域像素是否和种子点构成联通区域，从而决定是否对该区域进行填充，直至找到该区域内所有像素或达到轮廓线的边界。其分离的结果如图10 所示。

图10 曲线分离结果

2.4 线型判断

本文讨论的机械工程类图纸线型如下[18]：粗实线、细实线、点画线、虚线。如图11 所示，其中ab 为粗实线，cd 为点画线，ef 为虚线。

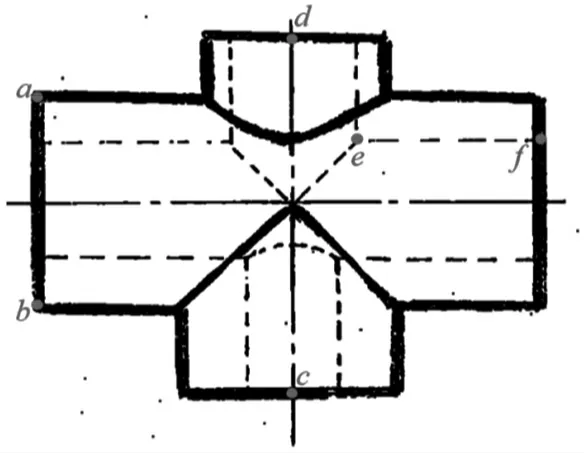
图11 输入图像

受人为绘制习惯不同，使用传统的图像识别算法对线型判断具有很大的误差，故本文采用基于卷积神经网络的图像分类算法对工程图图像进行识别。

2.4.1 数据集构建

为较好地还原手绘工程图实际情况，本文选取的数据集均来自实际手绘工程图及其图线线型。对每张工程图中每条图线建立ROI 区域，并截取ROI 区域构建工程图数据集。其部分ROI 区域如图12 所示。

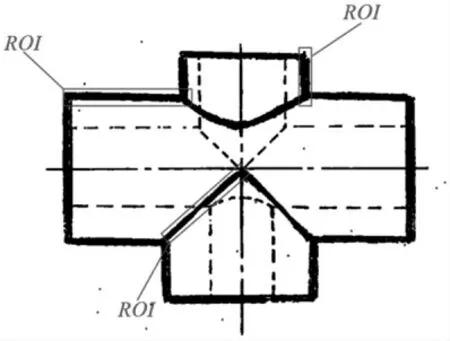
图12 ROI 区域示意图

本文对50 张工程图，共计2 000 条图线建立ROI区域，共得到2 000 张数据集，在实验过程中随机划分其中的70%作为训练集、20%作为测试集、10%作为验证集，对于每张图片随机采用图像旋转、亮度变化、图像正则化等图线增强算法后，输入到构建的分类神经网络中。其数据集类别及其特征见表1。

表1 数据集类别及特征

2.4.2 分类神经网络构建

卷积神经网络（CNN）是目前最为常见的一种神经网络模型，其主要被用于目标分类、目标检测、追踪等领域。卷积神经网络利用图片之间的相关性对图像进行轮廓提取操作，目前经典卷积神经网络有AlexNet、VGG、ResNet 等[19]。本文基于常见CNN 网络设计的工程图图线分类网络模型如图13 所示。将输入图片缩放到100×100 像素，工程图图线图像具有R、G、B 三个维度通道，因此网络将原始工程图图像转化为100×100×3的三维矩阵。同时利用具有8 层卷积层、4 层池化层的CNN 网络将转化后的三维矩阵卷积成6×6×128 的多维矩阵。利用3 个全连接层及Softmax 函数将多维矩阵展平并分类，分别获得节点数为512、256、4，最终将输入图像分为4 类，即粗实线、细实线、点画线、虚线。

图13 分类卷积神经网络结构图

2.4.3 分类实验结果与分析

在本文图线分类实验中，网络设计参数如下：初始学习率为0.000 1，迭代次数为100 次，采用Droupout及Adam 优化算法。图线分类训练过程准确率及Loss变化曲线图如图14 所示。

由图14 可知，经过100 次迭代，模型在训练集上的准确率为98.96%，其最终Loss 值为0.003 2。表2 给出测试集中4 种线型类别的混淆矩阵。其中每一行表示每一类图线识别为其他类别的概率，对角线表示每一类图线识别为本类别的概率，由该表可知，4 类图线的识别准确率均在90%左右，其中虚线的识别准确率达到93.2%。但在某些特殊情况下，粗实线和细实线之间可能会存在识别错误，点画线和虚线间可能会存在识别错误。

表2 图线图像分类混淆矩阵

图14 训练准确率及Loss 曲线图

3 算法应用

随着我国大力发展机械、电气、建筑等工程事业，越来越多的学生报选工科专业。其中制图类课程是众多工科专业重点必修课，国内从事制图类课程的授课老师数量众多，存在大量的课后作业和期末试卷需要老师修改。因此较好的工程图图线识别技术在制图教学领域具有重要意义[20]。本文通过在上述算法基础上增加坐标转换及曲线一致性判断算法对30 张学生试题答案进行自动评分，其算法应用流程如图15 所示。

图15 算法应用流程图

3.1 坐标转换

通常工程类作业对答案绘制位置有一定要求，本文通过在试卷答题区域附近绘制“L”型符号进行试题定位。在单幅工程图中所得出的点坐标均为绝对坐标，为和试题答案进行对比，应按照一定规则将检测出的直线端点的绝对坐标及曲线上所有点的绝对坐标转换为相对坐标。本文采取的转换规则如图16 所示，以定位点O为原点，按X 方向和Y 方向各点到该点的距离大小进行点的坐标转换，例如转换后点A 的相对坐标为（x0-x，y0-y）。

图16 坐标转换示意图

3.2 曲线一致性判断

对于直线而言，两点间最多存在一条直线，因此只需判断端点及线型是否正确。但两点间的曲线可能存在无数条。因此采用如下算法进行曲线一致性判断：

如图17 所示，假设λP={P0，P1，P2，...，Pn}是标准曲线上所有点的集合，λQ={Q0，Q1，Q2，...，Qn}是比对曲线上所有点的集合。从曲线最左端遍历到曲线最右端，若其中超过一定比例点的坐标差△y 小于设定阈值，则可近似认为该两段曲线一致性判断正确，反之则认为两段曲线一致性判断错误。

图17 曲线一致性判断

3.3 实验结果

本文选取了机械制图考卷中30 幅补画第三视图题型答案作为实验对象，该题型要求考生根据题目中给出的两幅视图绘制物体的第三个视图，其总分为15分，部分测试图纸如图18 所示。

图18 试题答案及部分考生测试图纸

本文采用的评分规则如下：（1）考卷直线及答案直线的两端点相对坐标值及线型关系相同则计分，反之则扣分；（2）考卷曲线与答案曲线的曲线一致性判断结果正确则记分，反之则扣分。采用上述算法及评分原则对测试试题进行自动评分。将自动评分结果与5 名人工评判得分的平均分进行比对，其评分结果对比图如图19 所示，其误差在10%以内，故本文算法在机械制图试卷自动评分方面具有一定的应用价值。

图19 评分结果对比图

4 结束语

本文提出了一种基于Hough 变换的工程图图线识别技术。对采集的工程图预处理后，利用Hough 变换、RANSAC 算法、最小二乘法检测出图像中直线，采用形态学开闭运算及漫水填充算法检测并分离曲线。采用卷积神经网络对各图线ROI 进行线型分类，得出工程图中线型关系。最后利用本文算法对选取的30 张机械类特定题型答案进行自动评分，并将其与人工评分结果进行对比，表明基于Hough 变换的工程图图线识别技术在教学领域具有一定的应用价值。本文算法在以下方面还存在不足：（1）当工程图较为复杂时，图线识别效果和理想结果会有较大差距；（2）工程图图线的识别速度还能进一步提升。