铝合金附着式升降脚手架在工程中的模拟分析

武 鑫

（河北工程大学 土木工程学院，河北 邯郸 056038）

随着我国人口的迅速增长，城市用地面积紧张，建筑结构转向高层及超高层发展是其必然的结果。脚手架是土木工程施工过程中为保证结构顺利进行的工作辅助平台，随着建筑物层数的不断增长、高度越高，传统的落地式脚手架不再满足现行业施工要求，随之附着式升降脚手架便应运而生。附着式升降脚手架其相对于传统落地脚手架有着诸多优势：（1）适用性强，能和各种不同结构的高层建筑相结合使用；（2）使用功能完善，具有智能提升一体化和防倾防坠等安全防护作用；（3）施工效率高，只需一次安装即可使用到整个结构完工，节省了大量人力物力，且随着结构越高其经济性也越大；（4）外表美观，与传统脚手架相比较，在施工现象中更加规整、简洁化，杜绝了以往施工现场的脏乱差现象，能更好地体现安全文明施工形象。

国内附着式升降脚手架在理论计算上十分成熟，对于其在模拟分析方面也颇有研究。赵飞[1]对以风荷载主导作用的高层建筑进行了分析研究，发现对于风振响应采用振型分解法更为可靠；王秀丽等[2]人以不同步运动下的附着式升降脚手架为研究对象，给出了满足其安全条件的指导性意见；周磊[3]根据有限元分析，着重研究了附着升降脚手架的静动力学方面的研究，得出了力学和变形的相关规律，为附着式升降脚手架施工和设计提供了依据。以上都是以全钢结构的附着式升降脚手架为研究对象。在铝合金结构方面的涉及甚少，卢玉龙等[4-5]人首先以全铝结构的附着式升降脚手架为研究对象进行了有限元模拟分析，但相关内容不够全面，需进一步补充相关研究。目前，在土木施工领域当中全钢升降脚手架还占据着市场的主要份额，但随着我国工业化的快速发展，铝合金材料相关工艺的提升，其在附着式升降脚手架上的应用也有着一定的发展前景。铝合金材料由其轻质高强的特点而得到广泛的应用，不仅如此它还有以下优点：（1）耐腐蚀；（2）工业性能良好（易加工、装饰效果好）；（3）经济性高（能够多次利用且回收率高）[6-7]。

1 研究内容及目的

采用6061-T6 牌号的铝合金材料，材料参数见表1，建立一种全铝附着式升降脚手架（以下简称为爬架）的有限元模型为研究目标，通过Midas Gen 进行数值模拟，在不同荷载组合下分析其正常使用和升降使用两种工况下力学性能的变化规律，为今后的铝合金爬架设计和施工提供一定的实际意义。

表1 6061-T6 牌号的铝合金材料参数

2 有限元模型的建立

2.1 模型建立

本模型采用梁单元建立，主要构件包括竖立杆、水平横杆、导轨、走道板、底部水平桁架、吊点桁架、内外三角连接撑，各构件之间采用刚性连接。模型结构参数如下：竖向主框架之间的间距设置为6 m，爬架整体高度为14 m，长度为9.8 m，宽度为0.6 m，立杆水平间距为2 m，层高步距为2 m，如图1 所示；具体构件参数见表2。

图1 架体三维模型

表2 架体三维模型构件参数

2.2 荷载取值及组合

2.2.1 荷载取值

作用于爬架的荷载可分为永久荷载和可变荷载两类，可根据《建筑施工工具式脚手架安全技术规范》[8]确定荷载大小，包括以下内容：

（1）恒荷载

主要构件已建模，按照其自重考虑，在Midas Gen中可根据结构材料自动计算生成，除此之外电动升降葫芦重量按照集中荷载施加。

（2）活荷载

根据《建筑施工工具式脚手架安全技术规范》，不同工况下活荷载取值见表3。

表3 不同工况下活荷载取值

为能反映实际施工过程，在正常使用工况下，活荷载施加于最上面两层走道板上；在提升工况下，活荷载施加于最下面两层走道板上。

（3）风荷载

风荷载根据《建筑施工工具式脚手架安全技术规范》，按公式（1）计算：

式中：wk为风荷载标准值（kN/m2）；βz为高度z 处的风振系数，一般取为1；μs为风荷载体形系数，取1.3φ，其中φ 为挡风系数取0.6；μz为风压高度变化系数，取C类地区150 m，μz=1.79；w0为基本风压（kN/m2）。

以上参数均按照《建筑施工工具式脚手架安全技术规范》取值，且根据《建筑施工脚手架安全技术统一标准》[9]要求六级及以上大风不得作业。由于本模型只考虑爬架重要受力构件，因此不再考虑防护网的作用，风荷载实际情况是先对防护网产生作用，接着传向爬架立杆。因此对于风荷载的施加进行面荷载向线荷载的一种转化，直接以线荷载的方式施加于立杆上，经计算等效为0.165 N/mm。

2.2.2 荷载组合

本文仅考虑正常使用和升降使用两种工况，并按照以下两种荷载组合效应进行有限元分析：

荷载组合1：1.2 恒载+1.4 活载，

荷载组合2：1.2 恒载+0.9（1.4 恒载+1.4 风载）。

根据规范要求，在正常使用工况条件下，其设计荷载值应乘以附加荷载不均匀系数γ1=1.3；在升降、坠落工况下，其设计荷载值应乘以附加荷载不均匀系数γ2=2.0。

2.3 边界条件设置

2.3.1 正常使用工况

当结构模型处于正常使用工况时，对最下排2 个支座（共设置6 个附墙支座）自由度全部约束，即：Dx=DY=Dz=0；上边两排4 个支座仅约束其水平自由度，Dx=DY=0。

2.3.2 升降使用工况

在升降使用工况时，爬架6 个附墙支座全部仅约束水平自由度，即：DX=DY=0；在下吊点位置处约束全部自由度，即：DX=DY=DZ=0。

3 有限元模型计算结果及分析

3.1 正常使用工况

3.1.1 荷载组合1

正常使用工况荷载组合1 下架体的变形和应力图如图2-图3 所示。在荷载组合1 作用下，架体整体变形呈现S 曲线型，有向外倾斜的趋向，最大位移发生Z 方向上，发生位置在中间走单板位置，最大竖向位移为9.69 mm，位移变形均满足要求；架体最大应力为96.63 N/mm2，发生在与内测立杆连接的走道板主龙骨位置上，架体各构件应力均处于容许范围内。

图2 架体在荷载组合1 下变形图

图3 架体在荷载组合1 下应力图

3.1.2 荷载组合2

正常使用工况荷载组合2 下架体的变形和应力图如图4-图5 所示。在荷载组合2 作用下，架体整体向内弯曲，在有风荷载参与下，中间位置由附墙支座约束，在架体上下两端形成悬臂结构，且此荷载组合下最大位移为Y 方向的位移，位移为32.71 mm，发生在架体最顶部外立杆位置，分析原因是由于上部杆件形成悬臂结构，造成在此处位移过大且超过L/400（L 为受弯杆件的跨度），除此位置外其他构件均满足位移变形要求；在考虑风荷载参与下，架体的Z 方向上的位移有所减小，但并不明显；架体最大应力为160.64 N/mm2，发生在与内测立杆连接的走道板主龙骨位置上，架体各构件应力均处于容许范围内。

图4 架体在荷载组合2 下变形图

图5 架体在荷载组合2 下应力图

3.2 升降使用工况

3.2.1 荷载组合1

升降使用工况荷载组合1 下架体的变形和应力图如图6-图7 所示。在荷载组合1 作用下，架体整体变形仍呈现S 曲线型，但相对于正常使用工况下有所减小，分析其原因是由于活荷载的减小所导致的，最大位移在Z 方向的底部走道板位置，位移为4.18 mm，变形位移均满足要求；架体最大应力为59.74 N/mm2，发生在架体底部内测水平桁架位置上，架体各构件应力均处于容许范围内。

图6 架体在荷载组合1 下变形图

图7 架体在荷载组合1 下应力图

3.2.2 荷载组合2

升降使用工况荷载组合2 下架体的变形和应力图如图8-图9 所示。在荷载组合2 作用下，架体整体向内弯曲，其架体变形原因与正常使用工况一致，但位移有所增大，此荷载组合下最大位移为Y 方向的位移，位移为35.65 mm，发生在架体立杆最顶部位置，除此位置外其他构件均满足位移变形要求；和正常使用工况相同，在考虑风荷载参与下，架体在Z 方向上的位移有所减小但不明显；架体最大应力为94.14 N/mm2，发生在架体底部内测水平桁架位置上，架体各构件应力均处于容许范围内。

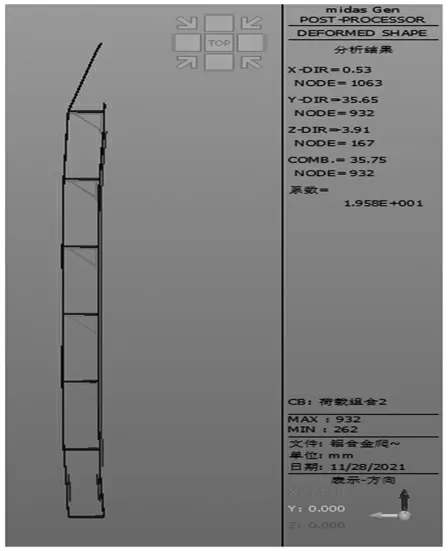
图8 架体在荷载组合2 下变形图

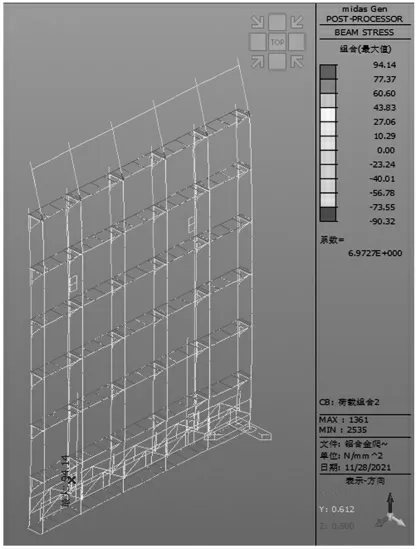
图9 架体在荷载组合2 下应力图

4 结束语

采用有限元软件Midas Gen 对于铝合金爬架建立模型，并在两种荷载组合下对爬架的正常使用和升降使用工况进行了静力学分析。得出主要结论如下：

（1）在不同工况的两种组合荷载下，铝合金架体各构件应力均处于容许范围内，验证了铝合金材料在爬架上的运用是可行的。在正常使用工况下，爬架架体最大应力出现在走道板位置上；在升降使用工况下，爬架架体最大应力出现在底部水平桁架上，因此建议在设计过程中对此位置进行加强，提高架体的安全系数。

（2）在不同工况下考虑风荷载参与组合时，其位移明显增大，尤其是在架体的顶部外立杆位置，除此之外其他构件位移变化均在容许范围内。在设计和实际施工过程中，可设置斜撑或抛撑，防止架体水平位移过大。

（3）在考虑风荷载参与的荷载组合下，对架体竖向位移产生有利影响，但作用不太明显。

（4）铝合金爬架在风荷载参与下，正常使用工况综合位移小于升降使用工况，说明架体在风荷载参与组合下提升架体施工风险较大，在实际施工过程中要严格按照规范操作。