隐私保护的群体感知数据交易算法

张勇，李丹丹，韩璐，黄小红

（北京邮电大学计算机学院（国家示范性软件学院），北京 100876）

0 引言

为了发掘数据中蕴含的潜在价值，打破“数据孤岛”，一些数据交易市场应运而生，如Infochimps、Datacoup、Microsoft Azure Market-place 等。数据消费者可以在这些平台上搜索和购买他们所需要的数据[1-2]。然而，当前这些平台的数据大部分是机构或组织出于自身的业务需求而保存下来的数据，无法满足数据消费者多样化的数据需求，从而使数据的可用性大打折扣[3-4]。因此，从多样性的角度来看，当前交易市场中的数据还十分有限，无法满足日益增长的数据交易需求。为解决这个问题，学者们提出了一种新的数据交易模式，即群体感知数据交易（CDT,crowd-sensed data trading）。CDT 采用移动群体感知技术为数据消费者提供数据资源，即数据提供者使用手机、平板电脑等智能设备按照数据消费者的需求为其收集数据[5-6]。

典型的CDT 系统（例如Thingful、Thingspeak）包括数据交易平台（以下简称为平台）、数据消费者（以下简称为消费者）和感知任务参与者（以下简称为参与者）。平台根据消费者的任务需求聘请大量的参与者，然后将参与者感知到的数据出售给消费者。当前，已有一些关于CDT 系统设计的工作。An 等[7]提出了一个基于逆向拍卖的群体感知数据交易系统，采用贪心策略来招募参与者，并保证拍卖过程的真实性。Zheng 等[8]提出了一个收益驱动的数据收集框架，采用拍卖机制来最小化数据收集的成本。Jiang 等[9]提出了一个基于质量感知的数据共享市场模型，从博弈论的角度分析了消费者行为，并提出了最优响应迭代算法来提高社会福利。

当前，大部分群体感知系统将平台建模为半可信的，即平台能够诚实地执行预定程序，但同时会分析参与者的数据进而窥探其隐私[10-11]。少数文献关注了群体感知数据交易市场中的隐私问题。其中，Gao 等[12]和Niu 等[13]使用同态加密和签名验证机制保护了数据交易过程中消费者的出价隐私和身份隐私。Zhao 等[14]提出了一种基于区块链的数据交易模型，采用环签名和相似性学习来保护参与者的身份隐私。当前的隐私保护方案主要针对消费者和参与者的身份及报价等信息进行保护，而如果将这些方案用于参与者的数据隐私保护，不仅效率低下，还会导致数据的可用性急剧下降。还有一些学者基于本地差分隐私提出了感知方案，允许参与者通过报告噪声数据来保护自己的数据隐私。Wang 等[15]基于本地化差分隐私提出了一种参与者位置保护方案。Xue 等[16]为保护参与者的隐私，基于本地化差分隐私提出一种个性化的隐私保护方案。然而，这些方案往往需要大量的参与者，在参与者数量较少的情况下，数据的实用性较差，而如果选取大量的参与者，则会增加平台的招募成本。基于此，本文提出了一种新颖的基于差分隐私的群体感知方案，参与者不再需要提交原始数据，而是提交对原始数据进行分析或计算得到的任务结果，同时通过对结果添加噪声来保护他们的数据隐私，噪声的分布是由平台分配的隐私预算来确定的。在这种情况下，平台可以通过对参与者隐私预算的动态调节来均衡结果的精度水平和相应的招募成本。

为激励用户参与群体感知数据交易，价格机制的设计也是需要考虑的问题。当前针对数据交易的价格机制研究主要考虑了数据量、数据质量等数据本身的因素[17-18]。例如，Yu 等[19]通过考虑数据质量和数据多版本发布的策略，提出了一个双层数学规划模型来优化数据交易。Jiao 等[20]考虑了大数据的“无限供给”性，提出了一种基于拍卖的大数据市场模型，通过拍卖机制得到最优的数据交易价格和交易量。黄小红等[21]基于数据质量、数据属性等多维因素构建了数据交易的价格机制。

本文提出的隐私保护的群体感知方案中，参与者上传的数据不再是原始数据，而是由数据分析得出的结果，并不具有上述方案中所考虑的数据属性，如数据量、数据质量等，因此不适用于上述价格机制。受到隐私数据发布的启发[22-23]，在满足消费者对结果偏差容忍的条件下，本文考虑了对参与者的隐私泄露补偿，以及平台的收益来优化数据交易。平台根据收到的消费者的偏差阈值、报价以及参与者的成本等信息，通过优化招募方案，在满足消费者偏差的容忍约束的基础上，最小化招募参与者的成本，最大化自身的收益。

因此，为了保护参与者的数据隐私，同时构建适用的价格机制，本文提出了隐私保护的群体感知数据交易算法。通过差分隐私聚合算法，平台聚合参与者的结果。对于结果的计算，可以采用参与者独立计算或者在平台的组织下所有参与者协同计算的方式进行。同时，本文提出了信誉模型，以确保参与者的可信性，在考虑消费者的偏差约束和参与者隐私泄露补偿的基础上，构建了交易优化模型，以最大化平台的收益。本文的主要贡献如下。

1) 为实现对参与者的隐私保护，以及保障数据的可用性，提出了基于差分隐私的数据聚合方案。平台为招募到的参与者动态地分配隐私预算。参与者根据收到的隐私预算，在计算得到的结果中添加噪声。这样既保护了参与者的隐私，又保证了聚合后结果的可用性。此外，为确保参与者的可信性，提出了信誉模型。

2) 为激励消费者和参与者进行数据交易，通过考虑消费者对数据偏差的容忍约束，参与者的隐私泄露补偿构建了交易优化模型以优化平台的收益。通过优化参与者的招募来提高平台的收益，并提出了基于遗传算法的收益优化算法（POA,profit optimization algorithm）来求解该模型。

3) 使用北京的天气和空气质量数据进行了实验，以评估模型的性能。结果表明，该模型不仅实现了对参与者的隐私保护，同时提升了平台的收益。

1 系统模型

1.1 群体感知数据交易框架

图1 展示了本文构建的群体感知数据交易框架，其中包括消费者、平台和参与者。消费者将任务发送给平台，平台按照任务的需求招募参与者，同时为每个参与者分配隐私预算。参与者收集数据并将分析或计算出的结果在添加噪声后发送给平台。平台聚合参与者的结果以完成消费者的任务。

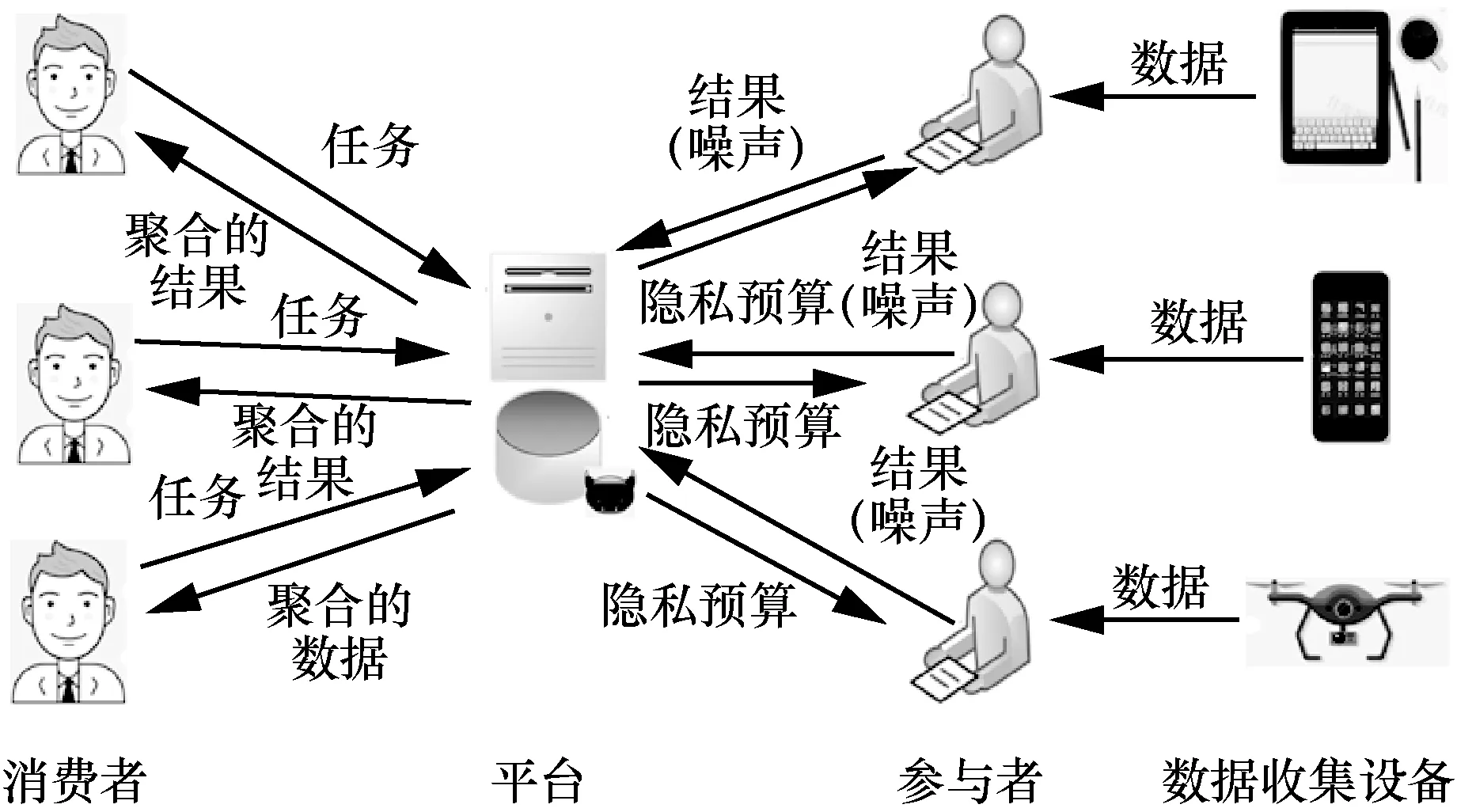
图1 群体感知数据交易框架

群体感知数据交易框架中包含3 种实体：消费者、平台和参与者。

1) 消费者是向平台发布任务的数据消费者。消费者会将自己的任务及相应的描述发送给平台，同时，以优化自身的满意度为目标确定报价和期望的偏差阈值。

2) 平台是群体感知数据交易的组织者。平台在收到消费者的任务后，会根据任务描述分析出完成该任务所需要的数据属性等，并招募相应的参与者以完成任务。在招募过程中，平台会以最大化自身的收益为目标，同时也需要为招募的参与者分配隐私预算以满足消费者的偏差要求。根据任务需求，平台也可以组织参与者进行联邦学习等协同计算以得到任务需求的结果。

3) 参与者是搜集数据的数据提供者。在收到平台所公布的任务要求后，参与者将自己所能满足的要求及相应的报价发送给平台，报价包含硬件成本（硬件损耗、能源消耗等）和隐私泄露成本。参与者收集数据，通过统计分析、数据挖掘或协同计算等方式得出消费者所需要的结果，并按照平台给出的隐私预算添加噪声后发送给平台。

1.2 数据交易流程

数据交易的过程如图2 所示，其具体流程如下。

图2 数据交易流程

1) 消费者将想要查询的任务发送到平台，其中包括对任务的详细描述、所能支付的报酬及期望的偏差阈值。

2) 平台对消费者的任务描述进行分析，提取出所需收集的数据属性以及需要计算的标签，然后将这些要求发送给参与者。

3) 参与者将自己所能收集的数据属性及相应的报价发送给平台。

4) 平台查询交易记录，以计算参与者的信誉值。平台以最大化自身的收益为目标确定招募的参与者，并为每个参与者分配隐私预算，随后将招募结果及隐私预算发送给相应的参与者。

5) 参与者根据任务的需求收集数据，并利用所收集的数据进行统计分析、数据挖掘或在平台的组织下进行协同计算以得出消费者想要的结果（即相应的标签），再根据平台分配的参数添加噪声后发送给平台。

6) 平台聚合所有参与者的结果，并将聚合的结果回复给消费者。消费者将报酬支付给平台，平台按照参与者的报价将酬金支付给参与者。

2 群体感知数据交易模型

本节将描述基于差分隐私的聚合方案，并构建数据交易优化模型。

2.1 问题描述

本节在描述问题之前，给出系统参数和变量的含义，如表1 所示。

表1 系统参数和变量的含义

在当前的CDT 方案中，平台招募参与者收集数据，然后将数据出售给消费者，但是过程中可能泄露参与者的隐私。为保护参与者的隐私，本文基于差分隐私提出了聚合方案。参与者在计算出任务的结果后，将按照平台分配的隐私预算添加噪声，随后将结果发送给平台。同时，为确保参与者的可信性，避免招募恶意的参与者，本文提出了参与者的信誉模型。最后，为了激励用户参与交易，通过考虑消费者对结果偏差的容忍约束和对参与者的隐私泄露补偿，本文建立了以平台收益最大化为目标的交易优化模型并进行了求解。因此，本节将描述提出的差分隐私聚合方案、信誉模型和交易优化模型的构建及求解。

2.2 差分隐私聚合方案

将图1 所示平台记作P。一段时间内，P收集消费者的任务请求。令U表示消费者集合，U中包含J位消费者，uj∈U，1≤ j≤ J，uj向P提交任务 γj，所有任务的集合为Η，

设参与者的集合为W，wi∈W，1≤i≤ I。wi对任务 γj计算得到ri,j，ri,j∈[0,1]，添加的噪声为φi,j，则P对于任务 γj聚合得到的结果为

其中，fj(·) 表示聚合函数，为参与者结果的加权求和；qi,j表示wi针对任务 γj的归一化权重；xi,j是一个二值函数，xi,j∈{0,1}，xi,j=1表示wi被选中来参与任务 γj，xi,j=0表示wi未被选中；Wj表示被选中参与任务 γj的参与者的集合，设Wj中参与者的数量为K，0≤ K≤ I。

聚合后结果偏差可以定义为

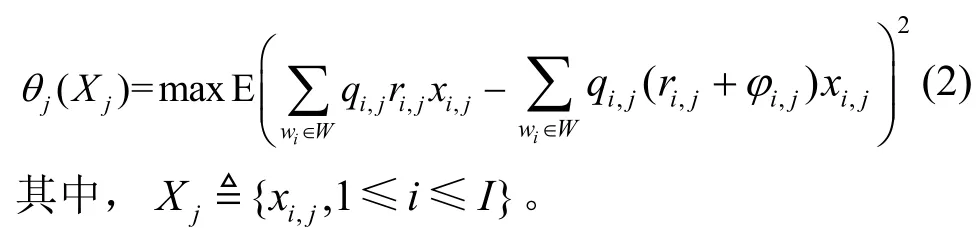
CDT 中需要考虑的是单个参与者的隐私泄露问题，主要应对差分攻击。差分隐私是一种应对差分攻击的有效方法。首先定义差分隐私。

定义1εi,j-差分隐私[24]。任务 γj的聚合函数fj:[0,1]K→ R 满足εi,j-差分隐私，则fj需要满足：若存在2 个只在第i位参与者的结果处存在区别的相邻向量(r1,j,…,ri′,j,…,rI,j)，fj对于任何一组聚合结果O⊆Range(fj)都满足式(3)，则fj满足εi,j-差分隐私。

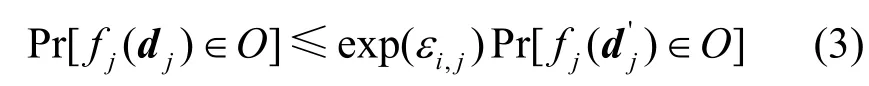
其中，εi,j是正的参数，用来表征隐私保护的强度，εi,j越小，隐私保护强度越大，隐私泄露就越少。因此，隐私预算 εi,j可以用来表征泄露的隐私量。

对于聚合函数fj，提供差分隐私的一个著名方法是将拉普拉斯分布得出的随机噪声添加到聚合函数[25]。由于本文方案允许每个参与者自己增加噪声，因此需要仔细设计噪声，使这些噪声的和等于从拉普拉斯分布中得到的随机噪声，即聚合噪声服从拉普拉斯分布。

结论已知所有参与者的xi,j和qi,j，在聚合函数fj下，针对任务 γj每个参与者的隐私预算和聚合结果的偏差可表示为

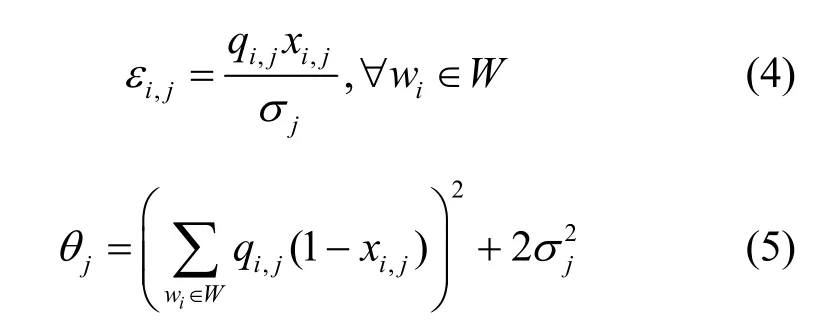
证明已知所有参与者的xi,j和qi,j，在聚合函数fj下，敏感度为

等式变换(a)是由拉普拉斯分布的可分性得到的，φj是一个均值为0、方差为的拉普拉斯随机变量。

如此，构建了参与者的隐私预算和结果偏差与参与者选取的关系。从式(8)和式(9)可以看出，参与者越多，结果偏差越小，但是隐私预算越大。从直观上说，对于相同的任务，参与者越多，结果越精确，但每个参与者的隐私损失越大。此外，还需要仔细选择参与者，因为他们有不同的信誉值（即qi,j），这也会导致不同的偏差。同时，不同参与者的成本也不同。因此，需要寻找一组合适的参与者来完成感知任务。

在得到Xj后，P会为每个参与者分配隐私预算，并聚合他们的结果，具体算法如算法1 所示。

算法1差分隐私聚合算法

4) end for

5) P 聚合参与者的结果（式(1)），得到回复给消费者的任务结果rj

需要注意的是，由于添加的噪声服从拉普拉斯分布，因此算法1 适用于计算结果是连续型的情况。证毕。

2.3 信誉模型

当前已经有一些研究通过度量参与者的工作能力来确定其信誉值，但平台需要知道参与者的一些信息如计算能力、存储能力、所处位置、轨迹信息等，这些信息中往往蕴含着用户的隐私[28-29]。因此，本文方案通过参与者在任务中的表现来设计信誉模型，基于参与者所提供的结果的准确程度来度量参与者的可信性，不再需要参与者提供上述隐私信息。参与者所提供的结果越精确，参与者的可信性越好，相应的信誉越高。不失一般性地，假设大部分参与者都是诚实的，会如实上报自己的结果。同时，用户在注册成为参与者时，平台一般会进行一些测试以确保用户有满足需求的工作能力[30]。

信誉模型是通过平台对参与者在任务中的评价而建立的。针对当前任务 γj，P对wi的信誉评价为

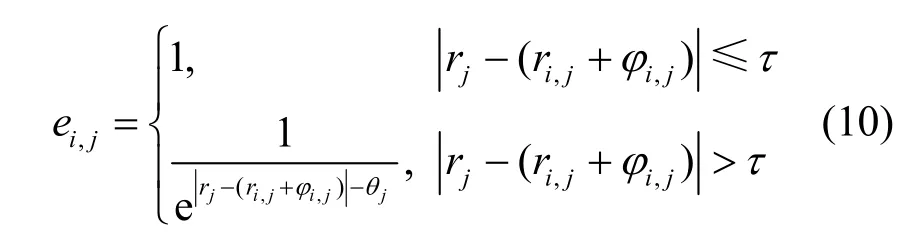
其中，τ 是固定的阈值，表示对误差的容忍程度。

P 会更倾向于选择近期进行过交易且信誉较高的wi，因此wi会存在累积信誉，并且交易时间越接近，对当前任务信誉值的影响就越大。设wi在一段时间内参与过Ψ 次P发布的任务，1≤ψ≤Ψ，影响参数越大表示距离当前任务越近，影响参数也越大。考虑时间因素，信誉模型可以更新为

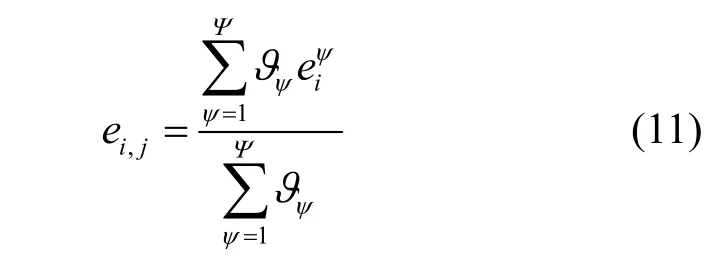
同时，任务的相似程度也是需要考虑的问题，与wi当前所参与的任务越相似，给出的评价越具有价值。采用任务所需要收集数据属性的杰卡德相似系数来度量2 个任务的相似程度[21]。因此，进一步考虑任务的相似程度，信誉模型可以更新为

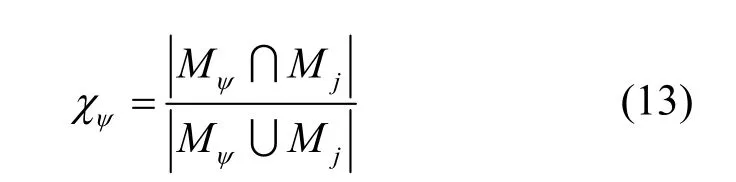
其中，Mψ是第ψ 次任务所需要收集的数据属性，Mj是P经过分析后认为完成任务 γj需要收集的数据属性。式(1)中采用的qi,j是通过计算ei,j并进行归一化得到的，即

2.4 交易优化模型的构建及求解

交易优化模型的目标是在满足消费者对结果偏差的约束及对参与者的隐私泄露补偿的基础上优化平台的收益。平台招募参与者以完成消费者的任务，因此平台的收益与消费者支付的报酬以及需要支付给参与者的酬金相关。

2.4.1 消费者支付的报酬

对于收到的结果，偏差越小，消费者从结果中得到的收益越大，但同时需要付出的成本也会越多，因此消费者会在收益和成本之间进行权衡。基于结果的偏差，构建消费者的满意度函数，它包含2 个部分：消费者从结果中所获取的收益以及需要支付的报酬。消费者通过优化自身的满意程度来确定最优的偏差，以及所支付的报酬。

设uj收到的结果的偏差为θj，uj可容忍的最大偏差为则uj的满意度函数可以表示为

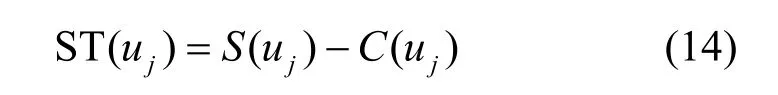
其中，S(uj)表示uj的收益，它是 θj的单调递减函数，即偏差越大所能获得的满意度越低。因此，构建 S (uj)为

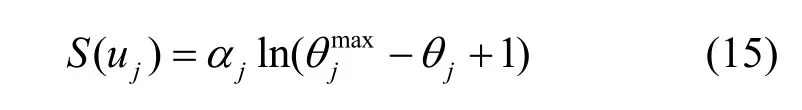
其中，αj表示固定的参数，由uj的特性决定，用来调整消费者对满意度函数和成本的侧重程度。

C (uj)表示消费者uj的成本，也就是消费者支付给平台的报酬，结果是偏差越小，需要支付的报酬就越大，理论上，θj越小，C(uj)的增长程度越大，因为精度越高，继续提高精度需要的成本越大[31]。因此，定义

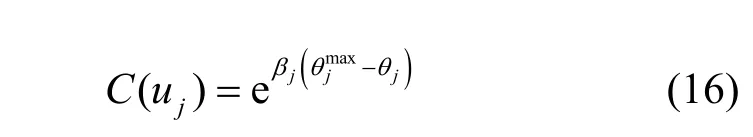
其中，βj表示固定的参数，由消费者对成本的容忍程度来决定。因此，ST(uj)的完整形式为

消费者的目标是最大化其满意度ST(uj)，也就是最小化(-S T(uj))。

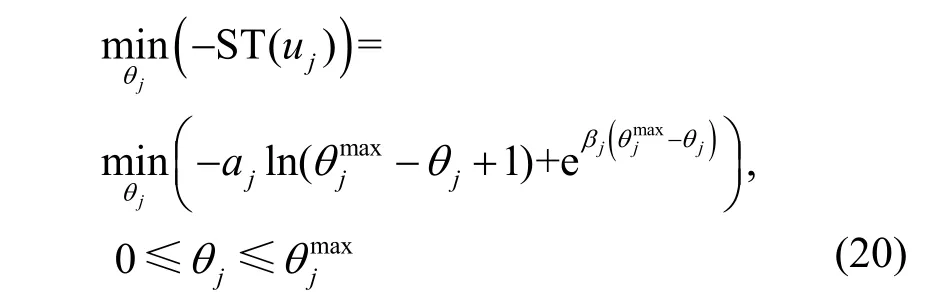
由于式(20)所示函数是严格凹的，且具有凸的约束，因此在KKT 条件下存在唯一的最优解。放宽约束，得到拉格朗日函数为

其中，λj和ηj是拉格朗日参数。

最优解满足以下条件

2.4.2 支付给参与者的酬金

wi在收到P发布的任务后，将针对 γj能够收集的数据属性Mi,j及报价发送给平台，设wi的报价为由2 个部分构成。一部分是wi完成任务 γj所需的固定成本，用hi,j表示，包含能源消耗、计算成本、数据传输成本等[32]。另一部分是wi的隐私成本，用pi,j表示，它与wi在任务中泄露的隐私成正比[22-23]。此时，参与者只需要上报单位隐私的价格，隐私的量可由平台给出的隐私预算得出。当wj放弃任务 γj时将回复bi,j=0。

假设wi被分配任务 γj，对于任务 γj，wi的隐私成本为

其中，ωi,j表示单位隐私预算的成本；εi,j表示泄露的隐私量，添加的噪声越多，隐私泄露越少，相应的成本越低。由于执行的任务都有时间限制，在划分的时间间隔内消费者只会被分配一个任务。平台支付给参与者的酬金为

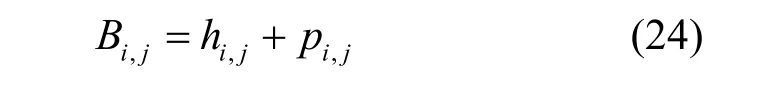
2.4.3 交易优化模型

交易模型的目标是最大化平台的收益，也就是从消费者处收到的报酬及支付给参与者的酬金之间的差值，因此可以将它的目标函数表示为

约束式(26)保证消费者得到的任务结果满足预期的偏差。约束式(27)表明当结果不满足消费者的预期偏差时，不会有参与者再进行此任务。约束式(28)说明参与者只有参与任务或不参与任务2 种状态。约束式(29)保证每个参与者最多只能参与一个任务。

2.4.4 收益优化算法

交易优化模型具有大量的变量且约束函数包含二值函数，很难采用数值方法进行求解，而采用遍历的方法计算复杂度较高，为JI，其中I和J分别表示参与者和消费者的数量。因此，本文基于遗传算法提出了POA，如算法2 所示。

算法2POA

3 实验结果

本文实验使用北京的天气和空气质量数据来提供空气质量预测服务。该数据集包含12 个空气质量监测站点的空气污染物数据。空气质量数据来自北京市环境监测中心。每个空气质量监测站点的气象数据均与最近的气象站相匹配。时间段是从2013 年3 月1 日到2017 年2 月28 日。因此每个数据集都包含35 064 条数据样本。每条样本包含时间、PM2.5、PM10、SO2含量等17 种属性。实验中，将每个空气质量监测站的数据分成10 份，并将每一份看成一个参与者收集的数据，因此实验中共引入了120 位参与者。为了使这120 位参与者的数据产生显著差异，实验中删除了某些参与者的一些数据属性。在实验过程中，参与者使用经典的机器学习算法（如线性回归算法等）提供空气质量查询、预测等服务。实验虚拟了10 位消费者，即J=10。实验平台为一台PC 主机，CPU 为i7-8700，主频为3.20 GHz，内存为32 GB，频率为2 666 MHz。

实验主要展示了消费者满意度函数随偏差的变化，POA 的收敛性、可扩展性及有效性验证，偏差和隐私预算随参与者选择的变化，消费者与参与者的变化对平台收益的影响及信誉模型的有效性验证。

3.1 消费者满意度函数随偏差的变化

消费者的满意度函数考虑了获取的收益和需要支付的报酬，为了展示最终的满意度、获取的收益及需要支付的报酬随偏差的变化，给出了消费者的满意度、获取的收益及需要支付的报酬随偏差的变化，如图3 所示。

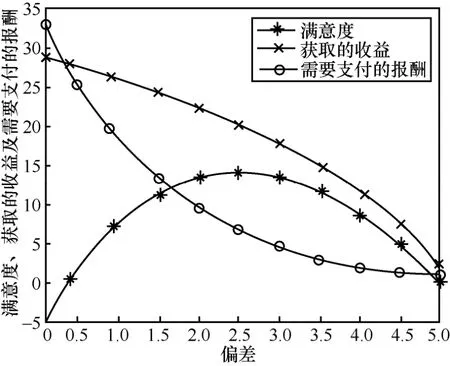
图3 消费者的满意度、获取的收益及需要支付的报酬随偏差的变化

消费者是从10 位消费者中随机选取一位。由图3 可知，随着偏差的增大，获取的收益和需要支付的报酬都逐渐降低，但获取的收益降低的速度逐渐加快，而需要支付的报酬降低的速度逐渐放缓。因此，消费者的满意度呈现先增长后降低的趋势。当偏差取2.4时，消费者的满意度达到最高值14.32，此时消费者需要付出的报酬为6.17。

3.2 POA 的收敛性、可扩展性及有效性验证

为展示算法的收敛情况，给出了平台的收益随迭代次数的变化，如图4 所示。

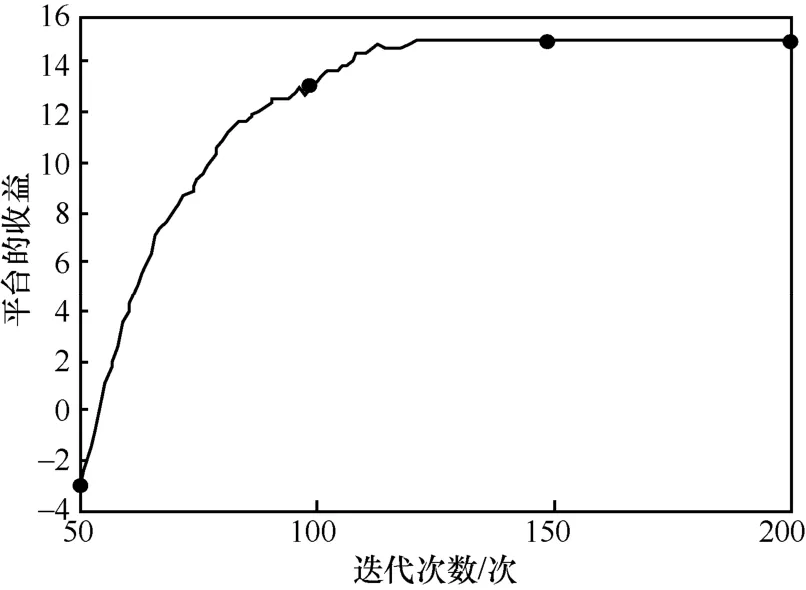
图4 平台的收益随迭代次数的变化

从图4 可以看出，随着迭代次数的增多，平台的收益逐渐增长。当达到一定的迭代次数后，收益的增长速度逐渐放缓，并最终趋于稳定。算法在120 次之内可以达到稳定状态。

为了验证算法的可扩展性，给出了迭代次数随消费者和参与者数量增长的变化，如图5 所示。

图5 迭代次数随消费者和参与者数量增长的变化

图5 中标注的数字表示“消费者数量+参与者数量”，如“5+120”表示此次实验中包含5 位消费者和120 位参与者。从图5 可以看出，随着消费者和参与者数量的增加，算法的迭代次数呈线性增加。这一结果验证了POA 对大规模数据交易系统具有较高的可扩展性。

为进一步展示POA 的有效性，将其与VENUS、DPDT 以及穷举法的实验结果进行了对比，实验结果如图6 和图7 所示。其中，VENUS 是Zheng 等[8]提出的一种基于贪婪策略的群体感知数据交易方案，以联合优化利润最大化和支付最小化问题；DPDT 是Gao 等[34]提出的一种满足差分隐私的群体感知数据交易机制，采用差分隐私拍卖的方法来实现数据定价和数据收集。

图6 几种算法在平台的收益方面的对比

图7 几种算法在运行时间上的对比

从图6 和图7 可以看出，穷举法具有最高的收益，但它的运行时间远超其他3 种算法。相比于VENUS 和DPDT，POA 在平台的收益方面分别提高了29.27%和20.45%，达到了穷举法的98.15%，运行时间也仅略高于DPDT。从平台的收益和运行时间综合来看，本文方案取得了最好的效果。

3.3 偏差和隐私预算随参与者选择的变化

按照本文方案中构建的参与者选择与隐私预算和偏差的关系，对于相同的感知任务，被选中的参与者越多，偏差越低，但同时会导致每个参与者有更高的隐私预算，从而泄露更多的隐私，为此，给出了偏差和隐私预算随被选中的参与者数量的变化，如图8 所示。

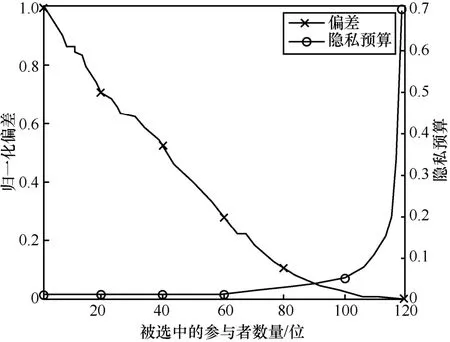
图8 偏差和隐私预算随被选中的参与者数量的变化

从图8 可以看出，随着被选中的参与者的数量增加，偏差逐渐减少，但每个参与者的隐私预算逐渐增多，且随着参与者数量的增长，隐私预算的增长速度越来越快，这与前文的分析是一致的。参与者的信誉值也会对参与者的选取造成影响，为展示这种影响，给出了不同信誉值下偏差和隐私预算随被选中的参与者数量的变化，如图9 所示。

图9 不同信誉值下偏差和隐私预算随被选中的参与者数量的变化

图9 中，高信誉值情况下，参与者的平均信誉值为0.9；低信誉值情况下，参与者的平均信誉值为0.7。在选取相同参与者数量的情况下，高信誉值的参与者具有更低的偏差，同时他们的隐私预算情况基本重合，都出现了随着被选中的参与者数量增长隐私预算增长越来越快的现象。

为了展示隐私预算与数据效用之间的关系，给出了几种算法数据效用随隐私预算变化的对比，如图10 所示。

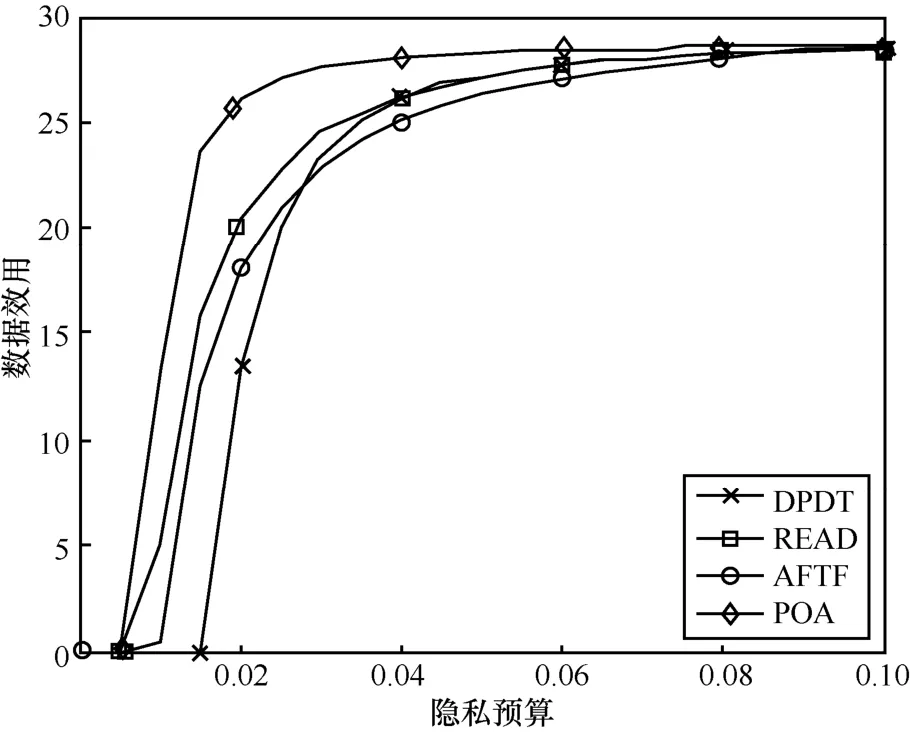
图10 几种算法数据效用随隐私预算变化的对比

图10 中，READ 和AFTF（partial arbitrage free trading framework）分别是Cai 等[35]和Zheng 等[36]提出的基于差分隐私的数据交易算法。隐私预算可以用来表征隐私保护力度，两者成反比，隐私预算越小表示隐私保护力度越强。数据效用是利用数据为消费者带来的收益来计算的。从图10 中可以看出，随着隐私预算的逐渐增长，即隐私保护力度的逐渐减小，数据效用逐渐增加，并最终稳定到最高值。从几种算法的对比来看，在相同的隐私保护程度下，POA 可以带来更高的数据效用。这是因为POA 采用的差分隐私聚合算法考虑了拉普拉斯分布的可分性，将拉普拉斯分布构造为多个独立同分布的伽马分布的和，使每个参与者所添加的噪声之和等于从拉普拉斯分布中得到的随机噪声。相比于取噪声最大值的传统拉普拉斯机制，对于每位参与者来说，可以使用更少的噪声添加来提供更高的隐私保护力度。因此，相比于其余几种算法，POA 在相同隐私保护力度情况下的参与者所需要添加的噪声更少，从而带来了更高的数据效用。

图11 展示了平台的收益随隐私预算的变化。当隐私预算很小时，任务的偏差无法满足消费者的需求，此时平台无法承接消费者的任务，因此收益为0。随着隐私预算逐渐增大，可以达到的任务偏差会逐渐减少，当满足任务需求时，平台开始承接消费者的任务。随着所承接任务数量的增长，平台的收益急剧增长。此时，由于支付给参与者的隐私成本最小，平台也可以获取最大的利润。随着隐私预算继续增大，平台从消费者处获取的任务报酬没有变化，但支付给参与者的酬金逐渐增长，平台的总收益与每笔任务的平均收益会逐渐减小，最终归于零收益。因此，在收到消费者提交的偏差需求及报酬后，平台会仔细挑选参与者，在满足消费者偏差需求的基础上，尽可能地减少隐私预算，以最优化自身的收益。而减小隐私预算，则意味着对参与者隐私保护的增强。

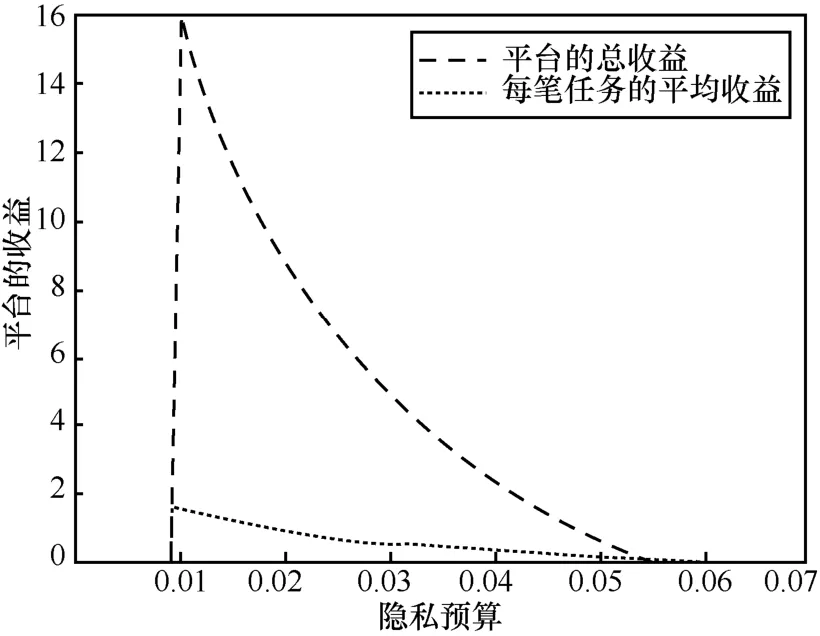
图11 平台的收益随隐私预算的变化

图12 展示了高信誉值、低信誉值和不考虑信誉值的情况下平台收益的变化。从图12 可以看出，随着迭代次数的增长，3 种情况下平台的收益都逐渐增长，并最终达到稳定状态。当达到稳定状态时，高信誉值情况下的平台取得了最高的收益，信誉值的考虑确实提升了平台的收益，而且参与者的信誉值越高，提升的幅度越大。这也说明了平台会更倾向于选择具有高信誉值的参与者，从而督促参与者在任务中诚实表现以提升信誉值。

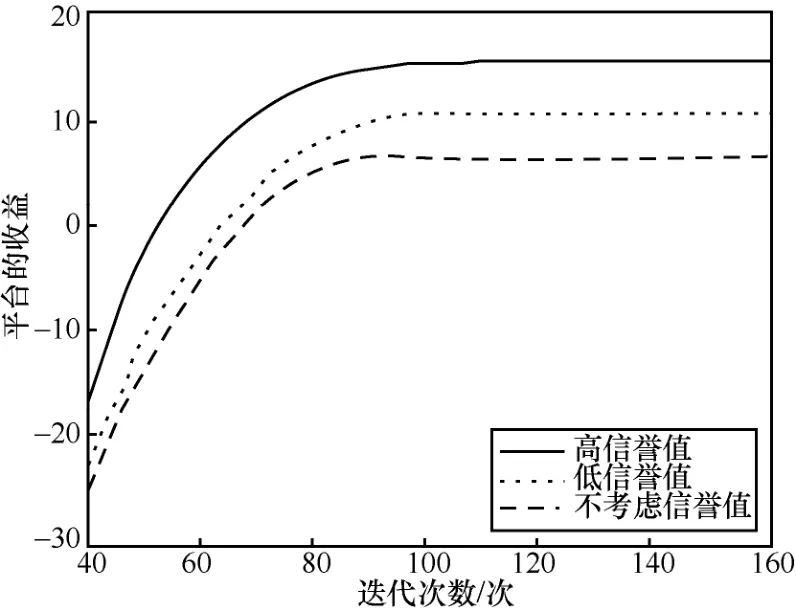
图12 信誉对平台的收益的影响

3.4 消费者与参与者的变化对平台收益的影响

为展示消费者和参与者的数量变化对平台的收益的影响，给出了平台的收益及被选中的参与者数量随消费者数量的变化和平台的收益及完成的任务数随参与者数量的变化，分别如图13 和图14 所示。

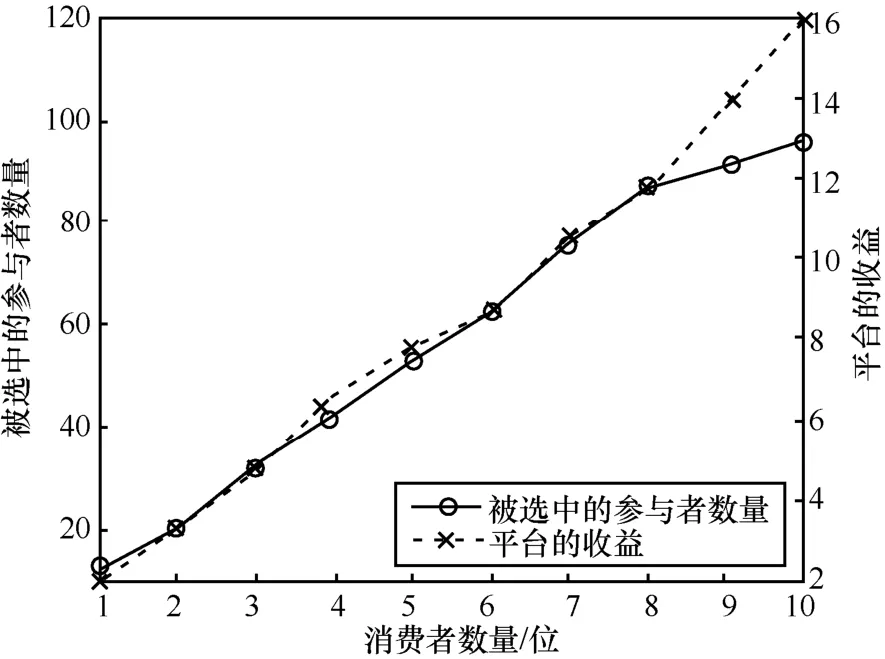
图13 平台的收益及被选中的参与者数量随消费者数量的变化

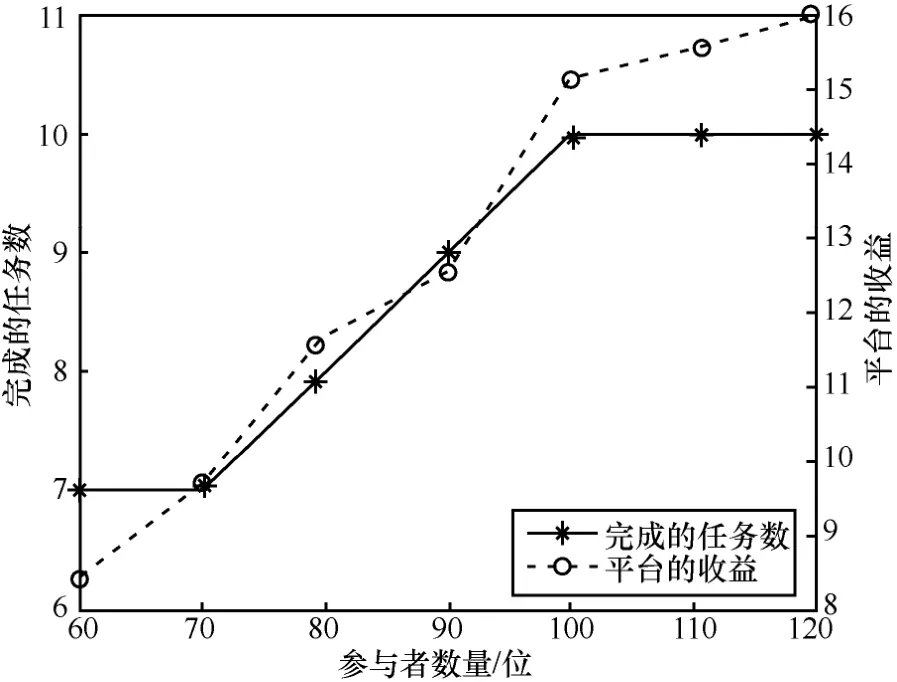
图14 平台的收益及完成的任务数随参与者数量的变化

从图13 可以看出，随着消费者数量的增长，被选中的参与者数量逐渐增加，所能完成的任务数随之增加，最终导致平台的收益也逐渐增加。从图14可以看出，随着参与者的数量增加，完成的任务数逐渐增多，当达到任务上限后，平台会对选取的参与者进行进一步优化，从而提高自身的收益。这说明消费者和参与者的增加都有利于提高平台的收益，这成为平台接受此模式并推动其发展的动机。

3.5 信誉模型的有效性验证

为了验证设计的信誉模型是否能够反映参与者在任务中的表现，本节设计了2 种参与者，一种是普通的参与者，他会正常完成任务，并且在任务中逐步提升结果的精确度；另一种是恶意的参与者，他开始也像普通的参与者那样表现，但达到一定次数后会发动攻击，即提供极差的结果，随后，恢复正常。两者的信誉值变化如图15 所示。

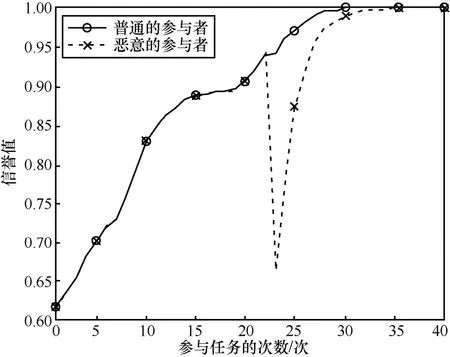
图15 信誉值变化对比

从图15 可以看出，随着结果精确度的逐渐提高，普通的参与者的信誉值随参与任务的次数的增多而逐渐增长，最终达到稳定。恶意的参与者的信誉值在他发起攻击时急剧下降，当他恢复正常后，他的信誉值也恢复正常的增长。这表明信誉模型对参与者的行为是敏感的。参与者“坏”的行为会体现在其信誉值上，从而促使参与者采取“好”的行为来提高信誉。

4 结束语

为了保护参与者的隐私，本文提出了一种隐私保护的群体感知数据交易框架。在此框架下，本文提出了基于差分隐私的聚合方案。参与者收集数据并进行计算，随后在计算结果中按照平台分配的隐私预算添加噪声，最后将分析结果发送给平台。这既保证了对参与者的隐私保护，又保障了聚合结果的可用性。此外，本文还提出了参与者的信誉模型，以保障参与者的可信性。通过考虑消费者的偏差约束和对参与者的隐私补偿，构建了以平台收益最大化为目标的交易优化模型，并提出了POA 进行求解，从而激励用户参与数据交易。基于北京的天气和空气质量数据的实验表明，本文方案在实现参与者隐私保护的基础上提升了平台的收益。