基于二维压缩感知的有意义图像加密算法研究

任花，牛少彰，任如勇，岳桢

（1.北京邮电大学计算机学院，北京 100876；2.河南师范大学现代教育技术中心，河南 新乡 453007）

0 引言

随着网络技术的快速发展，海量图像信息正在通过网络快速产生和共享，与此同时，未经授权的访问和滥用问题也随之涌现。作为一种重要的隐私保护技术，加密技术近年来受到了广泛关注[1]。当前的图像加密技术通常结合其他技术来提升加密安全性，如混沌理论[1-2]、DNA 编码[3-4]、光变换[5]、细胞自动机[6]等。虽然这些技术可以使密文数据不被直接获取，但是类噪声密文更易暴露被保护内容的重要性，不能确保密文的视觉安全性[7]。因此，如何提高密文的视觉安全性使其在传输时不易被暴露成为当前加密技术亟待解决的问题。

为了解决上述问题，Bao 等[8]在2015 年首次提出了有意义图像加密概念，通过加密技术和信息隐藏技术将一幅明文图像加密成另一幅有意义的加密图像。具体来说，先通过加密技术将输入明文图像转换成秘密图像，再利用信息隐藏技术将秘密图像嵌入一个较大尺寸的载体图像中。然而，Bao 等算法所生成的加密图像尺寸是明文图像的4 倍，增加了额外传输负担。幸运的是，压缩感知（CS,compressive sensing）可同步实现信号压缩和加密[9-10]。利用CS 将明文图像压缩加密成秘密图像，并通过调整采样率控制密文尺寸，有效解决了Bao 等算法存在的问题。

当前，大量研究已将CS 技术引入有意义图像加密机制中[11-20]。Chai 等[11]利用CS 技术将原始明文图像压缩加密成秘密图像，并将秘密图像嵌入离散小波变换（DWT,discrete wavelet transform）后的载体系数中，得到视觉安全的加密图像。由于DWT不可逆，对载体图像执行DWT 会影响秘密信息的正确提取。为了实现无损的信息提取过程，Wang等[12]和Chai 等[13]利用整数小波变换（IWT,integer wavelet transform）对载体图像进行无损变换处理，利用最低有效位（LSB,least significant bit）嵌入方法实现了小波系数的可逆修改。此外，为了降低CS测量矩阵所占用的空间，Wen 等[14]将半张量积（STP,semi-tensor product）测量矩阵构造方法应用到有意义的加密机制中。为了提高嵌入稳健性，Zhu 等[15]和Ye 等[16]利用奇异值分解（SVD,singular value decomposition）嵌入方法获得视觉安全的加密图像。为了解决LSB 嵌入不灵活及SVD 嵌入强度不高的问题，Wang 等[17]利用贝塞尔曲线嵌入方法实现有意义图像加密。然而，采用一维CS 压缩感知（1DCS,1-dimensional compressive sensing）[11-17]处理二维数字图像信号可能导致过高的存储计算负担[18]。基于此，Chai等[19]和Huo等[20]利用二维压缩感知（2DCS,2-dimensional compressive sensing）技术对明文图像进行压缩加密处理，通过修改载体图像的小波系数矩阵来嵌入秘密图像信息，有效提高了压缩性能和重构图像质量。

上述基于CS 的有意义图像加密机制[12,14-16,19-20]可归为两类。第一类机制[12,14-16,19]如图1 所示，发送端依赖持有密钥对明文图像依次执行CS 压缩-加密-嵌入操作，接收端使用相同密钥逆向执行提取-解密-CS 重构操作来恢复明文图像，此处，将CS 压缩之前采取的稀疏系数置乱过程视为CS 稀疏化过程。第二类机制[20]如图2 所示，发送端依赖持有密钥对明文图像进行加密-CS 压缩-嵌入操作，接收端使用相同密钥提取嵌入信息后，通过联合CS 解压缩和解密重构算法来恢复明文图像。在一些实际场景中，压缩之前需要执行图像加密过程。例如，当发送端无充足计算资源同时执行压缩和加密操作时，应首先实现加密确保隐私安全，然后将压缩的计算负担转移给计算资源充裕的第三方处理。文献[20]虽利用加密-压缩-嵌入操作，但由发送端完成整个操作不适用于预设资源受限的情况。此外，文献[20]还存在以下问题：1) 加密过程和明文无关联，使用相同置乱向量和相同扩散向量对不同明文图像加密会导致加密安全性不高；2) 预加密过程采取二维随机置乱（2DRP,2-dimensional random permutation）会导致重构图像质量不佳；3) 没有考虑待嵌入数据和待修改数据之间的关系，直接利用LSB 替换策略修改载体系数值在一定程度上降低了加密图像视觉安全性。

图1 第一类机制

基于此，本文提出一种基于2DCS 的有意义图像加密算法。首先，利用全局随机置乱和灰度变换操作产生预加密图像，以此作为二维压缩感知的输入生成秘密图像，并通过自适应嵌入技术将秘密图像加密成有意义图像。其次，采用二维投影梯度重构方法联合执行解压缩和解密操作，获取重构图像。实验结果验证了所提算法的有效性。

1 基础知识

1.1 压缩感知

假设二维图像和二维稀疏基为 X∈RN×N和Ψ∈RN×N，对X进行稀疏化，即

其中，(·)T是转置操作，D∈RN×N是稀疏基Ψ 上的系数矩阵。当D中的大多数元素为0 时，X可视为二维稀疏信号。通常来说，CS 用于一维信号采样。当CS 采样二维信号时，需将二维信号转换为一维信号后再采样，即

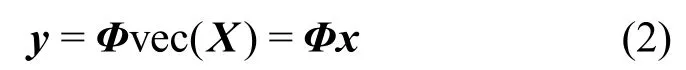
其中，vec(·) 是一维向量函数，x是 1 ×N2的一维向量，Φ∈RM2×N2和y∈RM2分别为测量矩阵和测量值向量。将二维图像数据转换为一维向量的采样过程称为1DCS。根据式(2)可知，1DCS 测量矩阵所占据的存储空间大小为 M2×N2，压缩过程的时间复杂度为 O (M2N2)。

与1DCS 相比，2DCS 的存储空间和时间复杂度更高效[21]。假设A和B是大小为M× N的2 个不同测量矩阵，利用2DCS 生成测量值 Y∈RM×M的过程如下

采样率SR 定义为

由式(3)可知，2DCS 的时间复杂度为 O (MN2)，只需2MN 个存储单元即可存储测量矩阵。

1.2 混沌系统

混沌是确定性非线性系统中普遍存在的一种现象，具有类随机行为，对初始条件和控制参数极为敏感[22]。与低阶混沌系统相比，超混沌是一类高阶混沌系统，在保密性、密钥空间及非线性行为方面比低阶混沌系统更具优势。因此，本文利用式(5)定义的超混沌系统生成混沌伪随机数序列[23]，即

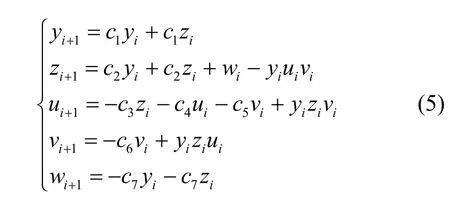
当五阶超混沌系统的控制参数设置为 [c1,c2,c3,c4,c5,c6,c7]=[30,10,15.7,5,2.5,4.45,38.5]时，式(5)处于混沌状态。

2 本文算法

本文提出的基于2DCS 的有意义图像加密算法框架如图3 所示。发送端借助外部密钥和明文图像的哈希值计算五阶超混沌系统的初始值，根据初始值生成伪随机序列，实现图像预加密过程；云服务器端对预加密图像执行2DCS 操作得到秘密图像，利用平滑函数[24]自适应地将秘密图像嵌入载体图像中，生成有意义加密图像；接收端提取嵌入信息后，通过二维投影梯度（2DPG,2-dimensional projected gradient）重构方法[21,25]同时进行解压缩和解密操作获取重构图像。2DPG 的每次迭代包括3 个过程：空域采用梯度下降法降低图像全变差（TV,total variation）[26]过程；小波变换域利用双变量收缩增强图像稀疏性过程；将迭代解投影到二维解空间过程。接下来将逐一讨论所提框架内容。

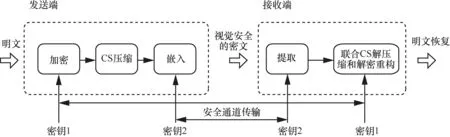
图2 第二类机制

2.1 图像加密

2.1.1 混沌伪随机序列生成

哈希函数因其不可逆性在图像加密系统中扮演着重要角色。MD5 和SHA-256 是2 种常用的哈希函数，分别生成128 位和256 位哈希值。为了提高加密安全性，本节的混沌伪随机序列由MD5 和SHA256 哈希函数控制生成。

首先，将256 位的外部密钥K分成32 块，即

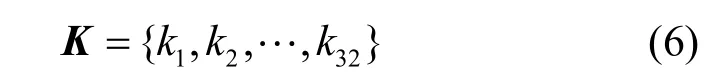
在式(6)的基础上，通过MD5 和SHA256 哈希函数，计算明文图像P0和外部密钥K的256 位哈希值H为

其中，S1、S2和S3分别计算P0的每一行像素和、每一列像素和以及对角像素和。

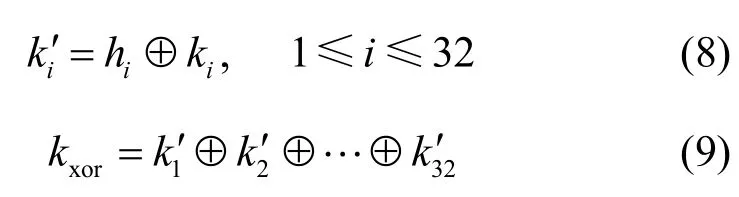
最后，根据 K ′和 kxor生成五阶混沌系统的初始值和伪随机序列，具体步骤如下。

1) 根据式(5)的默认方式设置五阶混沌系统的控制参数，利用 kxor和 K ′计算五阶混沌系统的初始值y0、z0、u0、v0和w0为

2) 为了消除混沌暂态效应，根据式(10)的初始值，循环迭代五阶混沌系统次，最后一次的迭代结果充当更新的初始值。

4) 通过式(11)，生成2 个长度均为 1 ×N2的混沌伪随机序列EP和ED，即

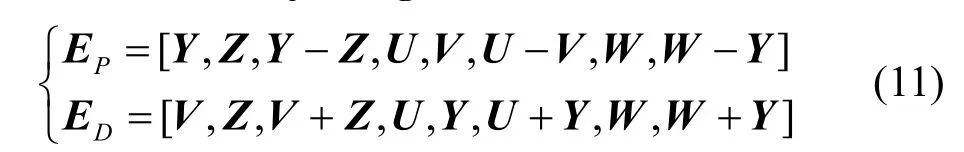
2.1.2 图像预加密

生成一维置乱序列EP和扩散序列ED后，发送端对明文图像执行全局随机置乱（GRP,global random permutation）操作和灰度变换操作，生成预加密图像。

首先，发送端将N× N的明文图像P0转换为1 ×N2的一维向量 vec(P0)；同时，利用内置排序函数排序一维置乱序列EP，得到 1 ×N2的位置向量POS。根据位置向量POS，对 vec(P0)执行全局随机置乱操作，即

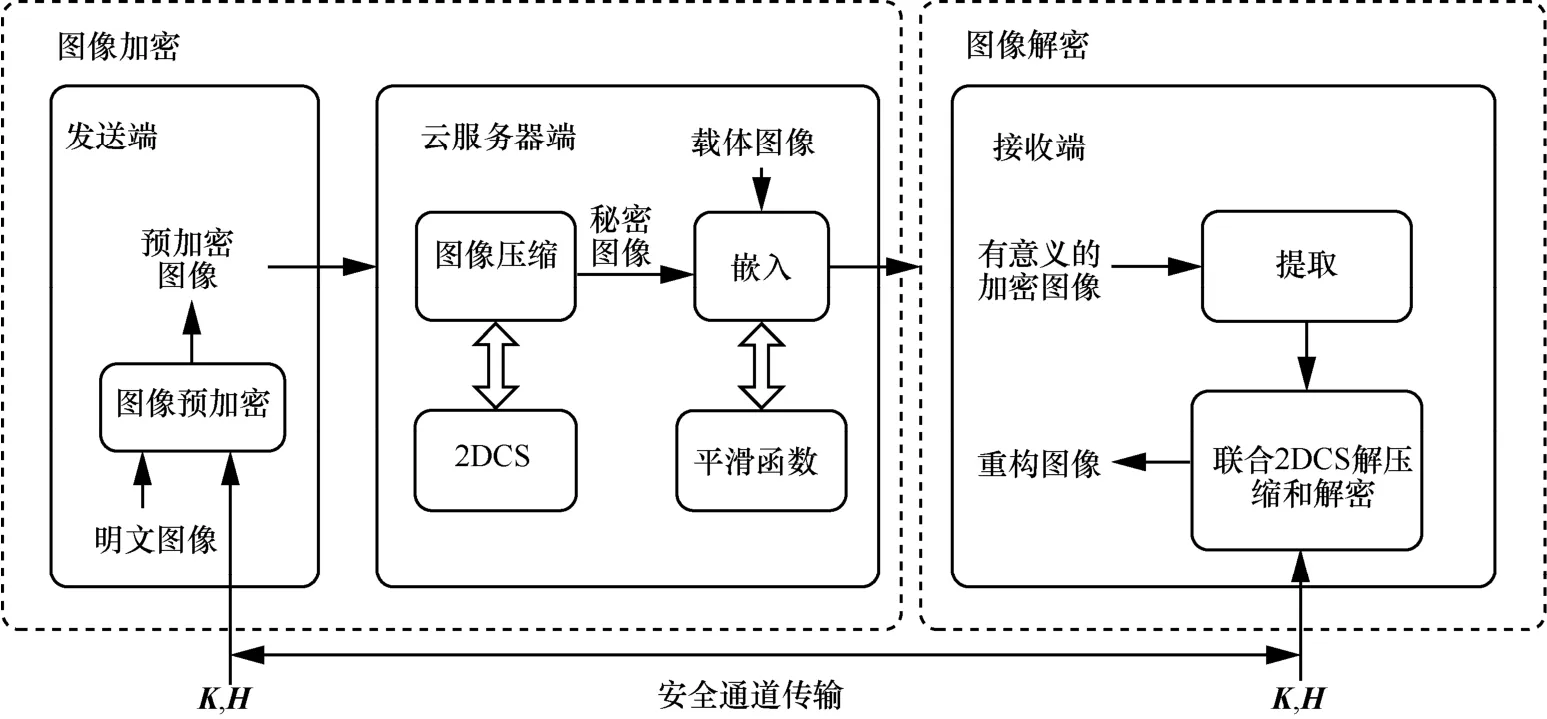
图3 算法框架

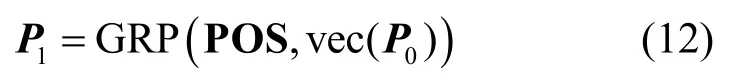
其中，P1是置乱后的一维向量，GRP(·) 是全局随机置乱函数。

随后，将置乱向量P1转换为二维矩阵，通过式(13)的灰度变换操作对P1完成扩散操作，即

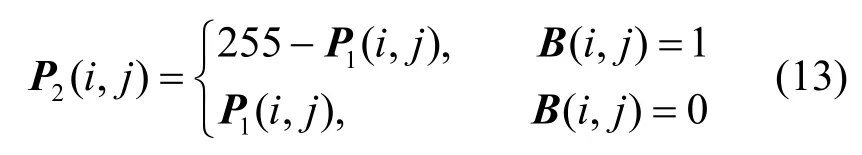
其中，矩阵P2是预加密结果；二值矩阵B由扩散矩阵ED计算，且 B=mod(ED×1014,2)，ED是已转换为二维矩阵的伪随机序列值。

2.1.3 压缩嵌入

云服务器端通过2DCS 操作将预加密图像P2压缩加密成测量值P3，将测量值P3量化到整数值[0,255]，生成秘密图像P4，再通过平滑函数嵌入方法将秘密图像自适应地嵌入载体系数矩阵中。具体步骤如下。

1) 构造M× N(M＜ N)的高斯随机测量矩阵A和B，并利用2DCS 将P2压缩加密成测量值P3，即

2) 利用非线性函数 Sigmoid 将P3量化到[0,255]，得到秘密图像P4为

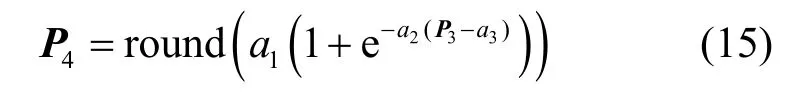
其中，round(·) 为四舍五入函数，a1=255，和min 是测量值P3中的最大值和最小值。

3) 将秘密图像P4排列成一维向量

6) 将含嵌入信息的系数向量转换为二维矩阵，利用LIWT 的逆变换过程将二维矩阵变换到空域，得到有意义加密图像P5。

2.2 图像解密

解密是加密的逆过程，主要包括秘密图像提取和明文图像重构过程。

2.2.1 秘密图像提取

2.2.2 明文图像重构

在图像重构阶段，以往有意义图像加密算法通常先根据解密密钥解密所提取的信息，再利用CS重构算法获取重构图像内容。与以往算法不同的是，本文采取二维投影梯度2DPG 重构方法[21,25]同时进行解压缩和解密操作生成重构图像。在图像重构前，通过安全通道将外部密钥K和哈希值H传输至接收端。

首先，利用逆Sigmoid 函数对所提取的秘密图像P4进行逆量化。

为方便后续理解和描述，将测量值P3赋给矩阵Y。紧接着，需对二维投影梯度迭代过程初始化，而Y=P3=AP2BT的最小L2范式解可视为初始值X0。

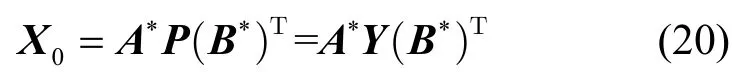
其中，A*=AT(AAT)-1和 B*=BT(BBT)-1分别表示A和B的伪逆矩阵。

然后，分别从梯度下降、双变量收缩和解投影3 个过程实现图像重构。首先，利用梯度下降法降低空域图像的TV。

其中，参数δ 用来避免分母为0，在本文实验中δ=10-7。

3 实验结果及对比

本节给出所提算法的仿真结果，所有实验均在64 位Windows7 PC 16.0 GB 和Inter(R) Core(TM)i7-4770CPU @ 3.40 GHz 上进行，平台为MATLAB R2012b。在混沌伪随机序列生成阶段，外部密钥为K=6b679b3c77826d30a79e612114a8c18df984c176 f4e529f684748ad052241b17。在2DCS 压缩和重构阶段，正交高斯随机矩阵作为测量矩阵，采样率固定为重构过程采取DDWT 作为稀疏基。利用峰值信噪比（PSNR,peak signal-to-noise ratio）和平均结构相似性（MSSIM,mean structural similarity）测量加密图像的视觉安全性和重构图像质量。

3.1 实验结果

本节以大小为256 像素×256 像素的标准测试图像Parrots、Monarch、Camera、Boats 和Barbara作为明文图像，Lena 作为载体图像，对所提算法进行测试。图4 给出了Parrots 和Monarch 的测试结果。由图4 可知，秘密图像已经压缩加密成了原始明文图像的，倘若在不安全通道直接传输，秘密图像的类噪声外观易引起攻击者的注意；如果传输加密图像，可以看出不同明文图像对应的最终加密图像视觉上类似，与载体图像Lena 无法用肉眼区分，因此可以在不引起攻击者注意下实现加密图像的安全传输。

需要说明的是，在有意义加密图像生成过程中，发送端只需要对二维图像进行预加密，此过程的时间复杂度为 O (MN)；云服务器端需要先对预加密图像进行2DCS 处理，随后完成嵌入操作，此过程的复杂度为 O (MN2)；接收端采取二维投影梯度重构方法解压缩解密加密图像，此过程的复杂度为O(MN)。因此，本文所涉及的加密算法的计算复杂度为 O (MN2)。

接下来，分别从直方图分析、相关性分析、信息熵分析、差分攻击及选择明文攻击（CPA,chosen plaintext attack）5 个方面验证所提算法的有效性。

3.1.1 直方图分析

图像直方图用来描述离散灰度值的概率密度分布。利用Lena 为载体图像，对5 幅明文图像进行加密，图5 给出了载体图像和加密图像的直方图结果。不难发现，不同明文图像所对应的加密图像具有相似的直方图分布，且与载体图像Lena 的直方图分布相似，这说明所提加密算法有效地隐藏了原始明文图像信息，攻击者难以通过加密图像的直方图分布分析明文关联信息。

3.1.2 相关性分析

对于视觉有意义的明文图像而言，相邻像素相关系数应接近于1。本文算法将输入明文图像加密成外观类似于载体图像的加密图像，所生成的加密图像的相邻像素相关系数值理论上应接近于载体图像的相邻像素相关系数值。相邻像素相关系数值的计算式为

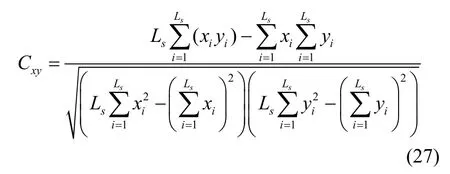
其中，xi和yi是2 个相邻像素值，Ls是随机所选的总像素对数。本节随机从水平方向、垂直方向以及对角线方向上选择Ls=2 000对像素进行测试。

图6 给出了Parrots 为明文图像、Lena 为载体图像的测试结果。图6(a)～图6(c)为载体图像Lena 在水平方向、垂直方向以及对角线方向的相关性，图6(d)～图6(f)为加密图像在水平方向、垂直方向以及对角线方向的相关性。从图6 可以看出，加密图像在水平方向、垂直方向及对角线方向上的相关性近似于载体图像，很难用肉眼逐一区分。进一步地，表1 列出了5 幅不同明文图像所对应的秘密图像、载体图像和加密图像在3 个方向上的相关系数值结果。从表1 中可以看出，加密图像的相关系数值接近于载体图像的相关系数值，这说明所提算法能够很好地将明文图像加密成外观类似载体图像的加密图像。

图4 Parrots 和Monarch 的测试结果

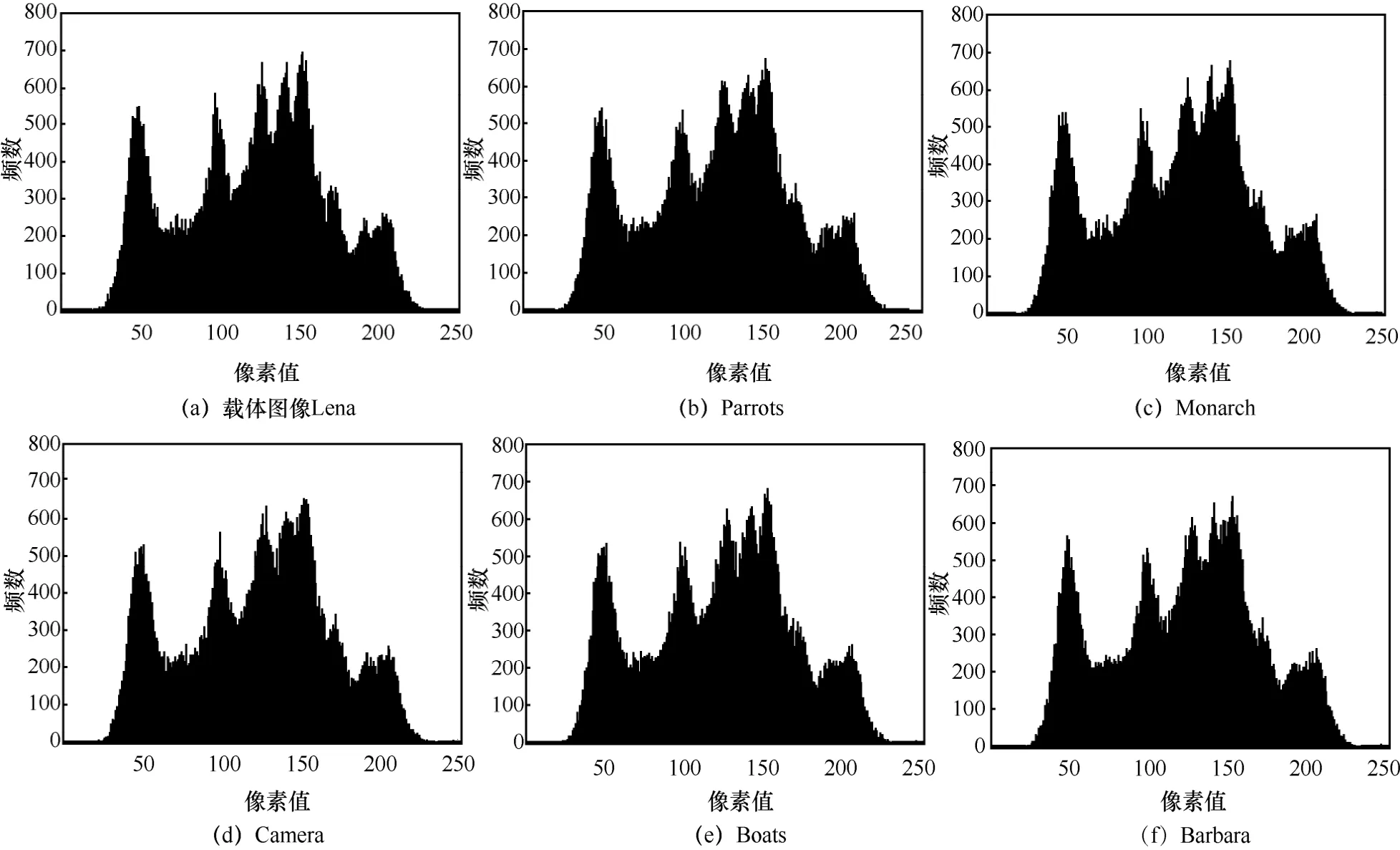
图5 载体图像和加密图像的直方图结果

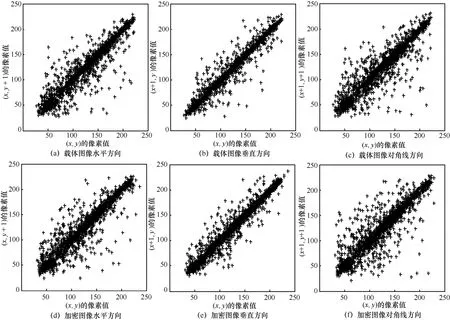
图6 Parrots 为明文图像、Lena 为载体图像的测试结果

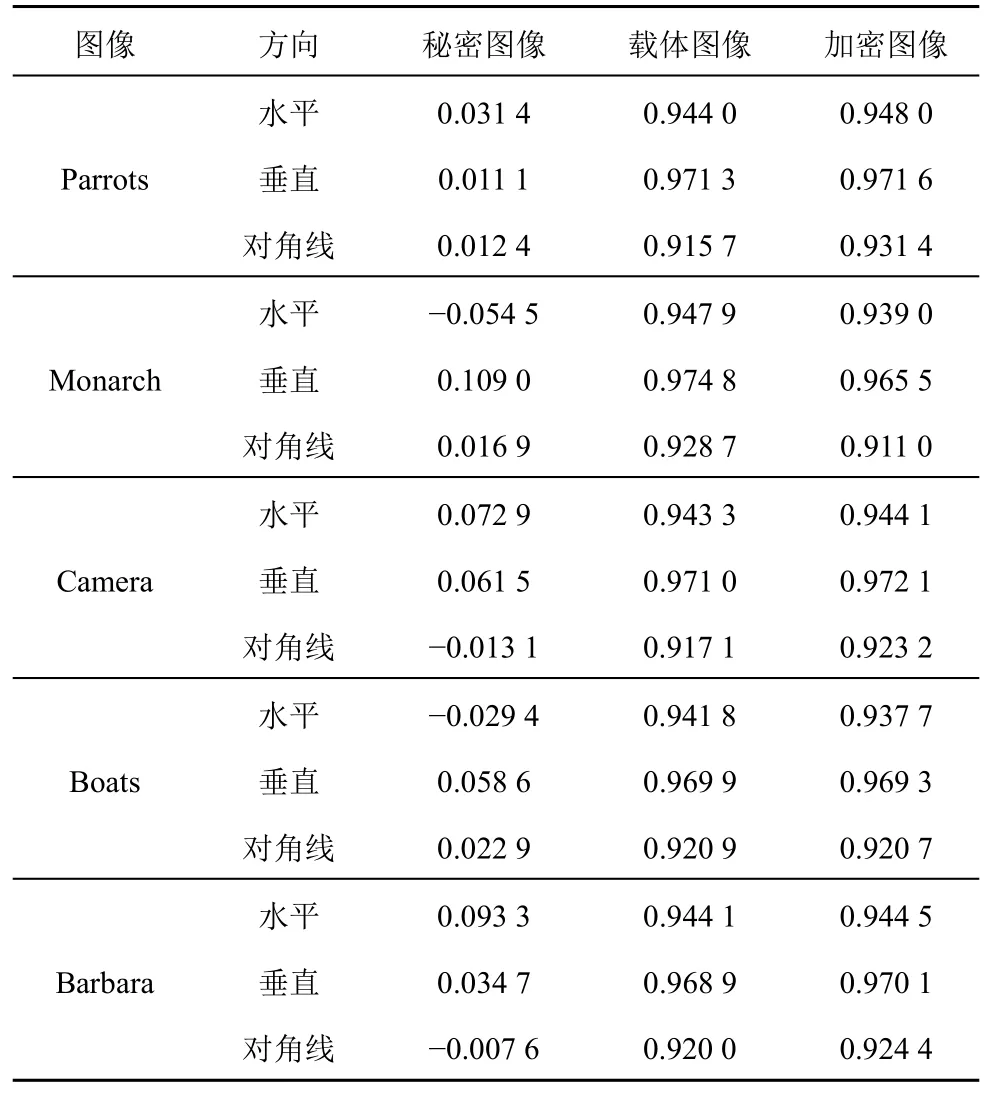
表1 相关系数值结果

3.1.3 信息熵分析

信息熵是评估加密安全性的重要指标之一。对于有意义加密图像而言，加密图像的信息熵越靠近载体图像信息熵，则加密效果越好。图像信息熵的计算式为

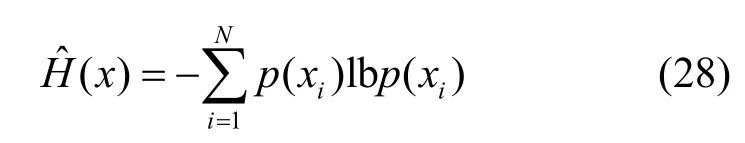
其中，p(xi)是xi的发生概率。表2 列出了将不同明文图像嵌入相同载体图像Lena 后的信息熵结果。

从表2 可知，加密图像的信息熵与载体图像的信息熵相关，随着载体图像的信息熵改变，加密图像的信息熵随之改变，这说明攻击者很难通过加密图像的信息熵来分析原始明文信息。

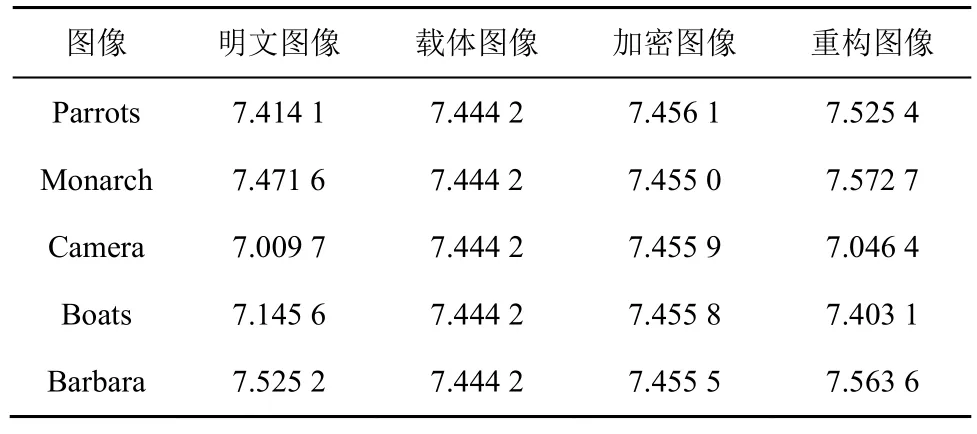
表2 信息熵结果

3.1.4 差分攻击

差分攻击指攻击者通过改变明文图像中的一个像素值，分析两幅加密图像之间的差异，建立明文图像和加密图像之间的关联，并尝试在未知密钥信息的前提下恢复明文图像。通常使用像素变化率（NPCR,number of pixels change rate）和统一平均变化强度（UACI,unified average changing intensity）来分析加密系统抵抗差分攻击的能力，计算式为

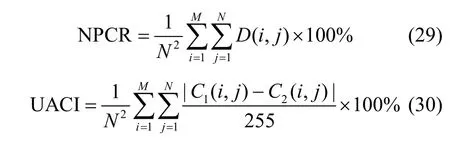
其中，C1和C2为在明文图像上稍加修改而获得的2 个加密图像。如果C1(i ,j )=C2(i ,j)，则 D (i ,j)=0，否则 D (i ,j)=1。

本文算法通过改变明文图像Parrots的1 bit像素和2 bit 像素，分别计算所生成的加密图像的NRCR 和UACI，结果如表3 所示。从表3 不难发现，1 bit 像素改变和2 bit 像素改变所生成的加密图像差异不大，最大NPCR 差异为0.43%，最大UACI 差异仅0.01%，暗示了通过差分攻击来攻破加密系统是无效的。

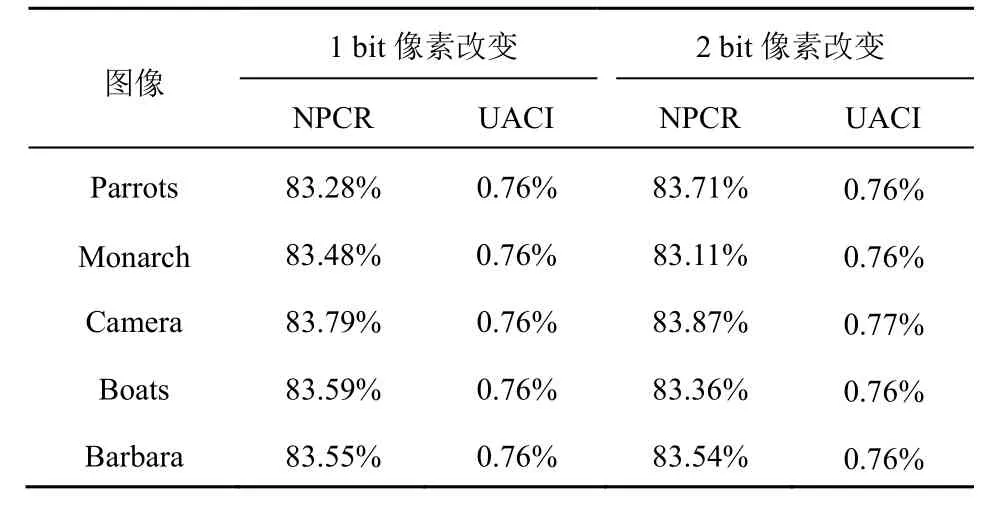
表3 NPCR 和UACI 结果

3.1.5 选择明文攻击

已知明文攻击（KPA,known plaintext attack）指攻击者在事先了解明文和相应密文的情况下试图揭露密钥关联信息的密码分析模型。与KPA 相比，选择明文攻击具有更强大的能力，攻击者可以选择任意明文并生成相应密文，以揭示密钥相关信息。如果一种加密方案能够抵抗CPA，则该方案也能抵抗KPA。基于此，安全的图像加密机制应该能够抗CPA。在本文算法中，虽然明文图像只改变了1 bit 信息，但所生成的秘密图像存在明显差异，这是由于加密过程的密钥由哈希值控制，而哈希值对明文极其敏感，微小改变的明文图像都会生成完全不同的预加密图像，从而生成完全不同的秘密图像。基于以上分析，本文算法可以抵制CPA。

3.2 比较

3.2.1 噪声和裁剪攻击

加密图像在不安全通道中传输时容易遭到噪声干扰，安全的加密算法应具备抗噪声干扰能力。本节将分析本文算法和文献[20]算法在抗噪声攻击方面的能力。在实验过程中，本文算法和文献[20]算法均采用二维投影梯度重构方法[21,25]重构原始明文图像。图7 给出了遭受不同强度椒盐噪声攻击后的加密图像以及重构图像结果。由图7 可知，当噪声强度从0.000 1 增加到0.001 0 时，文献[20]算法的重构图像PSNR 依次为29.142 8 dB、21.758 5 dB和18.423 5 dB，而本文算法的重构图像PSNR 依次为32.158 2 dB、26.522 0 dB 和20.382 2 dB。显然，本文算法的抗噪声干扰能力优于文献[20]算法。

为了测试抗裁剪攻击能力，将文献[20]算法和本文算法的加密图像的不同区域的像素值设置为0，相应结果如图8 所示。随着裁剪区域的逐渐增大，文献[20]算法的重构图像PSNR 依次为23.423 7 dB、20.142 6 dB 和16.854 8 dB，而本文算法的重构图像PSNR依次为27.288 9 dB、24.272 8 dB和18.354 2 dB。因此，无论是抗噪声干扰能力还是抗裁剪攻击能力，本文算法均优于文献[20]算法。

3.2.2 加密图像视觉安全性比较

为了进一步验证加密图像的视觉安全性，本节计算本文算法的加密图像和载体图像之间的PSNR 和MSSIM，并和文献[12,13,15,17,20]算法进行比较。在实验中，除上文测试图像Parrots、Monarch、Camera、Boats、Barbara 和Lena 外，对常用测试图像Peppers、Jet、Baboon、Girl、Goldhill 和Bridge 也进行了测试。同时，明文图像和载体图像实现一一对应，即不同的明文图像将生成不同的加密图像。表4 和表5 分别给出了本文算法和文献[12,13,15,17,20]算法的加密图像PSNR 和MSSIM。从表4 和表5 可知，本文算法的加密图像PSNR 和MSSIM 均高于其他算法。这是因为其他算法采取直接位替换操作修改载体系数值，而本文算法考虑了待嵌入数据和待修改载体系数之间的关系，有效降低了由于嵌入而造成的载体数据的修改幅度，从而提高了加密图像的视觉安全性。

图7 本文算法和文献[20]算法椒盐噪声攻击结果

图8 本文算法和文献[20]算法裁剪攻击结果

3.2.3 重构图像质量比较

为了分析重构图像效果，使用512 像素×512 像素的相同明文图像Barbara 及等大小的不同载体图像Lena、Boat、Je 和Peppers 进行测试，计算重构图像和原始明文图像之间的 PSNR 和MSSIM，并和文献[12,13,15,17,20]算法进行比较。具体实验过程中，文献[12,13,15,17]算法采用1DCS 先压缩明文图像再加密，对提取信息解密后利用正交匹配追踪（OMP,orthogonal matching pursuit）进行图像重构；而文献[20]算法和本文算法采用2DCS 压缩加密明文图像，利用二维投影梯度2DPG 方法同时进行解压缩和解密得到重构图像。表6 列出了不同算法的PSNR 和MSSIM 结果。从表6 中可以看出，文献[20]算法和本文算法的重构图像质量明显优于文献[12,13,15,17]算法，主要原因是利用基于2DPG 的图像重构效果优于OMP 图像重构。此外，文献[20]算法的重构图像的PSNR 和MSSIM 不如本文算法所生成的结果，这是因为文献[20]算法采取二维随机置乱2DRP 操作进行加密，而本文算法采取全局随机置乱GRP操作进行加密，利用GRP 加密在一定程度上提升了重构图像质量。

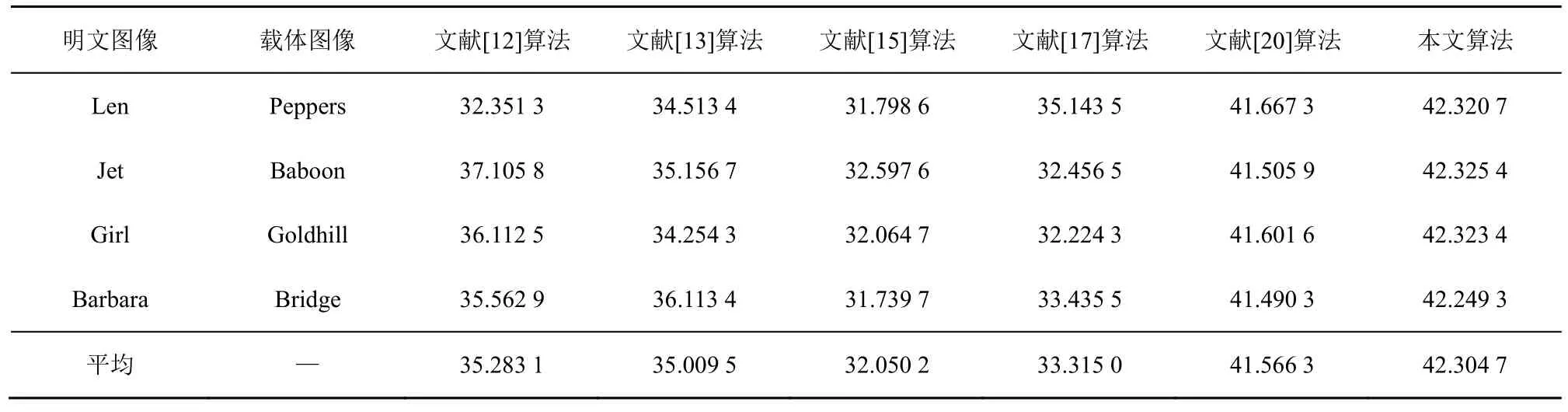
表4 加密图像PSNR 比较

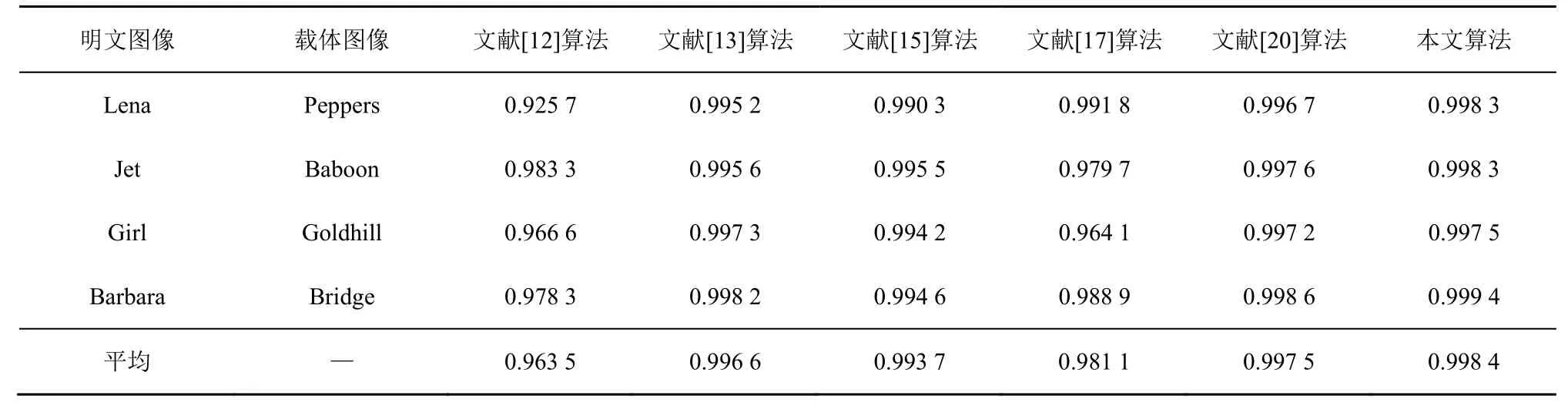
表5 加密图像MSSIM 比较

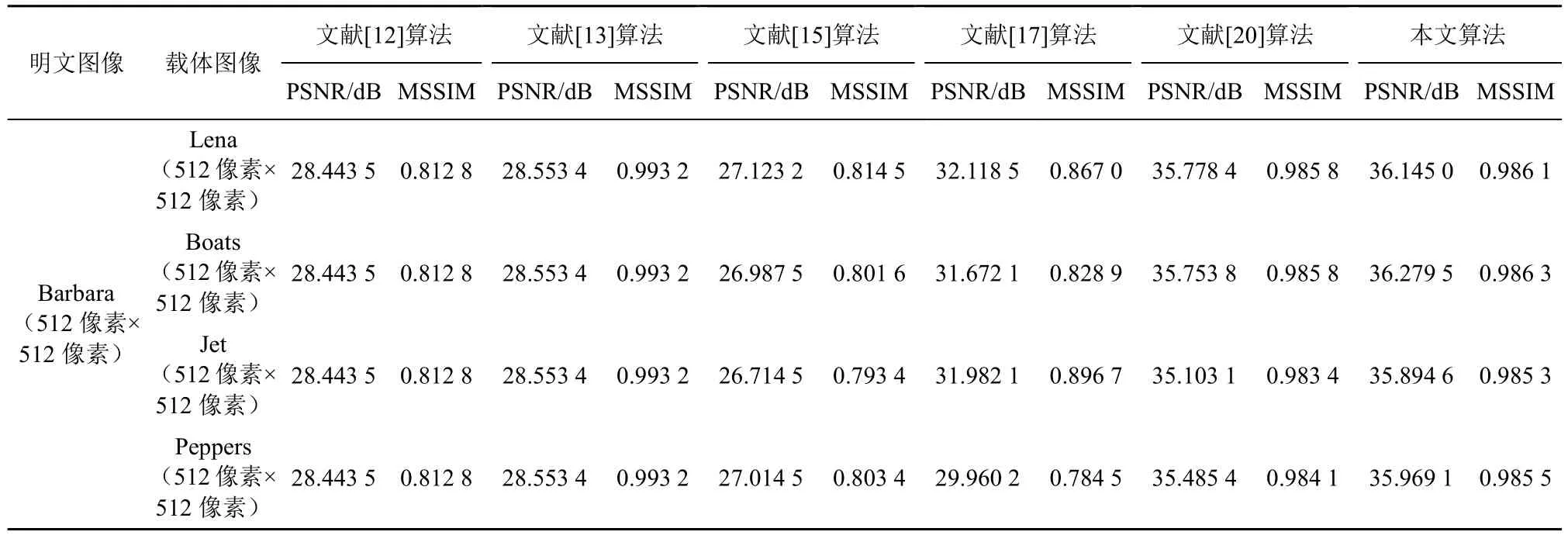
表6 重构图像PSNR 和MSSIM 比较

综上，本文算法具有更优的重构图像质量。

4 结束语

本文提出了一种基于二维压缩感知的有意义图像加密算法。首先，设计了一种与明文相关联的混沌伪随机数生成方法，在此基础上，利用GRP操作加密明文图像，提高了加密安全性且改进了重构图像质量。其次，利用平滑函数嵌入方法自适应地将秘密图像嵌入载体图像中，有效提高了加密图像的视觉安全性。然而，由于2DCS 的输入是预加密图像而非原始明文图像，当遭受噪声干扰时，在解压缩图像上进行解密会对重构图像质量造成一定的影响。下一步工作将考虑在压缩之前引入矢量量化操作，将量化后的误差矩阵作为2DCS 的输入，图像重构由矢量量化矩阵和重构误差矩阵联合完成，以提高有意义加密算法的稳健性。