软件定义网络中一种快速无循环路径迁移策略

燕昺昊，刘勤让,2，沈剑良，汤先拓，梁栋

（1.信息工程大学信息技术研究所，河南 郑州 450001；2.国家数字交换系统工程技术研究中心，河南 郑州 450001）

0 引言

软件定义网络（SDN,software defined network）通过集中式的控制逻辑实现了对流量的细粒度管理[1]。运营商可利用SDN 根据自身需求或网络状态随时调整策略部署而不需要考虑转发设备之间存在的硬件差异。因此，传统网络中需要复杂操作才可实现的路由优化、故障恢复等功能均可灵活实现。

路径迁移作为一种有效的性能优化机制及故障恢复手段，在SDN 管理中发挥了关键性作用[2]。网络中流的转发路径受突发情况影响无法时刻保持最佳传输状态。因此，为保证数据流正确传输，路径迁移技术通常为数据流同时规划多条转发路径。当原始转发路径发生拥塞或故障时，控制器将同时下发新的转发规则至新旧路径上的交换机，以引导数据流迁移至新路径传输。

然而，由于链路及设备状态差异，发往不同交换机的指令将经历不同的传输时延以及生效时间[3-4]。这种异步更新机制造成了流转发行为的不一致，导致包括更新循环、黑洞以及拥塞在内的一系列问题[5-6]，严重影响端到端服务质量，特别是在大规模网络环境下。其中，更新循环是路径迁移过程中频繁出现且易造成网络故障的关键问题之一，已经成为当前关注重点[2,7-8]。更新循环是指当迁移过程的新旧路径存在反向重叠时，不正确的节点更新顺序将导致数据包在节点之间往返，更新循环示例如图1 所示。图1 中，如果交换机v4在交换机v3之前更新，则将产生v3→v4→v6→v3的循环。对于交换机(v2,v3)同理。这种循环行为将极大地消耗链路带宽资源，进而影响正常数据流的传输，严重时可导致链路瘫痪。

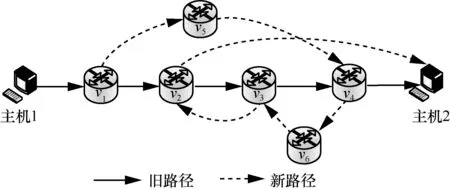
图1 更新循环示例

为避免路径迁移过程出现转发循环，研究人员深入探究了循环产生的原因并提出了许多代表性的工作。最早提出的代表性方法称为两阶段提交法[6,9]。在流更新期间，具有不同匹配标识的新转发规则被发送到交换机来替代旧规则。新到的数据包因为在头字段中具有不同于旧数据包的标签，如虚拟局域网（VLAN,virtual local area network）可被新规则识别并转发。旧规则最终将由于超时被删除。然而，同时保持新旧规则在交换机中会降低存储空间的利用率，且需要付出一个无关的包头字段的代价。

为解决利用率的问题，Zhou 等[10]提出了倒序更新机制。当新旧路径存在反向重叠时，一个节点的更新需要保证其在旧路径的上游节点先被更新。然而，倒序更新本质上给网络施加了强一致性约束，可能会导致不必要的更新时间。同样考虑图1所示的拓扑，交换机在新旧路径上处于反向重叠状态。因此，为满足循环更新依赖，倒序更新机制使交换机按照的顺序进行更新，更新时间为然而，本文通过观察发现，如果v2先被更新，则v3和v4处于“孤立”状态，因为此时没有任何流通过v3和v4。显然，在下一时刻，v3和v4可被同时更新而不会造成循环。此时，更新时间可缩减为

为加快更新过程，Wang 等[7]提出了基于分段的并行更新机制Cupid。通过将新路径上的节点分割为不存在依赖关系的更新片段并在段内施行倒序更新，可在保证无转发循环的同时实现多节点并行更新。在此基础上，Li 等[11]进一步改进了Cupid 并提出了新的更新方式RU。RU 的优势在于其实现了对段内节点的同步更新，即保证段内的第一个循环节点最后更新，且多段可以同时并行更新。然而，尽管2 种方法都使用了不同的约束机制加速了更新过程，但对于路径循环的检测依赖于求解有向无环图的强连通分量，时间复杂度为 O (E+V)。V 和E分别为新旧路径构成的有向无环图中节点和连边的数量。当待更新流的数量急剧增加时，时间开销将显著增加。

上述大部分工作只关注具体的实施方案及策略，而忽略了时间开销对路径迁移的重要性程度。快速的网络状态转移可有效减少数据包在交换机内的等待时长，进而节省交换机内部存储空间且避免数据包长时间等待而被超时丢弃。此外，即使部分工作涉及快速更新机制[7,11]，但并没有充分探索解空间，例如如何快速检测迁移过程中可能出现的循环问题。因此，在已有研究基础上，本文关注快速实现无循环路径迁移，包括检测和执行，以应对现有方案在实时性上的不足。具体地，本文提出了一种快速无循环路径迁移策略。该策略可同时缩短路径迁移中检测阶段和更新阶段的完成时间，进而实现整体迁移性能优化，提升网络收敛速度以及抗振荡能力。本文主要贡献如下。

1) 提出一种基于节点排序的快速循环检测（NRLD,node ranking-based loop detection）算法。NRLD 通过对新旧路径上的公共交换机进行编号并对比相邻交换机序号位置差异，实现了对路径迁移过程中是否发生循环及循环发生位置的快速检测。

2) 提出并分析了路径迁移过程中待更新交换机之间存在的松弛依赖关系，并基于NRLD 实现了松弛依赖关系的快速检测。

3) 提出一种基于节点松弛依赖关系的贪婪更新（RDGU,relaxation dependency-based greedy update）机制。基于获得的松弛依赖关系，RDGU 机制构建贪婪更新机制以保证每轮中可同时更新的节点数量最大化。

4) 通过仿真实验验证了提出的快速无循环路径迁移策略。相比于已有路径迁移中的循环避免方案，所提策略在不同网络环境下均可显著降低时间开销，有效提升路径迁移效率。

1 网络模型

本节首先对网络进行建模并给出路径迁移的相关形式化定义，然后建立优化目标函数并分析约束条件。

本文提出了流更新方案基于SDN实现。在SDN中，位于控制平面的控制器C负责为每个新到达的流f计算转发路径p并发送相关的规则r至交换机v。对于数据平面，使用无向图 G=(V ,E)表示由交换机集合和交换机之间的链路集合构成的网络拓扑。给出如下定义来描述路径迁移。

定义1路径迁移。对于任意流f，其转发路径从具有相同起始点sf和终点df的旧路径po迁移到新路径pn。

定义2无循环更新。对于po和pn中所有公共节点构成的有向图Gd，任意节点vc∈Gd的更新不得使流f经过的路径形成有向环，即流f不能经过同一节点两次。

因此，定义2 可表示为如下约束

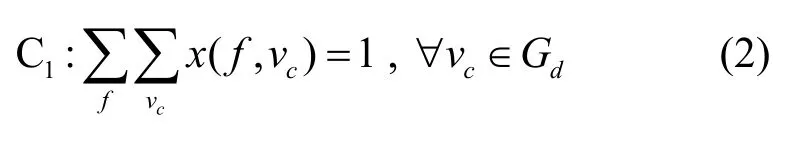
假设流f从旧路径po迁移到新路径pn在轮之内完成。因此期望找到一组迁移调度序列可以在满足定义2 的前提下使k最小化。因此，首先给出如下优化目标函数

2) 对于任意节点vi，进入交换机的流f只能匹配新规则rn或旧规则ro二者中的一个。

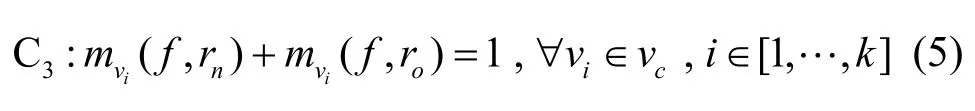
3) 对于任意节点vi，所有待更新流f所需新规则总数不得超过交换机剩余可用容量Rvi。

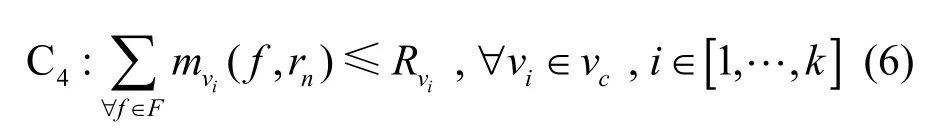
4) 对于任意节点vi，满足流守恒约束，即流入的流数量与流出的流数量相等。

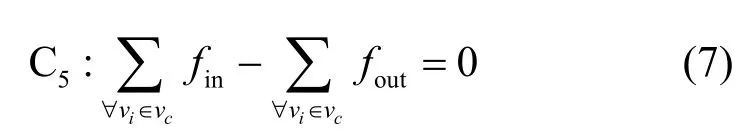
此外，本文中假设所有交换机vi∈V均由同一个控制器C进行管理。交换机之间的任意链路ej∈E容量充足，不会导致拥塞。表1 给出了网络模型相关参数及含义。

表1 网络模型相关参数及含义

2 算法设计

2.1 概述

本文提出的快速无循环路径迁移策略主要由基于节点排序的快速循环检测算法以及基于节点松弛依赖关系的贪婪更新机制构成，且均部署于控制器端。对于每个需要进行路径迁移的流，控制器首先调用循环检测算法判断其新旧路径是否可能发生循环。若不满足发生循环的条件，则直接将新规则下发至相应的交换机来实施路径迁移；否则，再次调用循环检测算法来发掘节点之间存在的松弛依赖关系。基于松弛依赖关系，控制器调用贪婪更新模块获得路径迁移更新序列并分步下发规则至相应的交换机。快速无循环路径迁移流程如图2 所示。

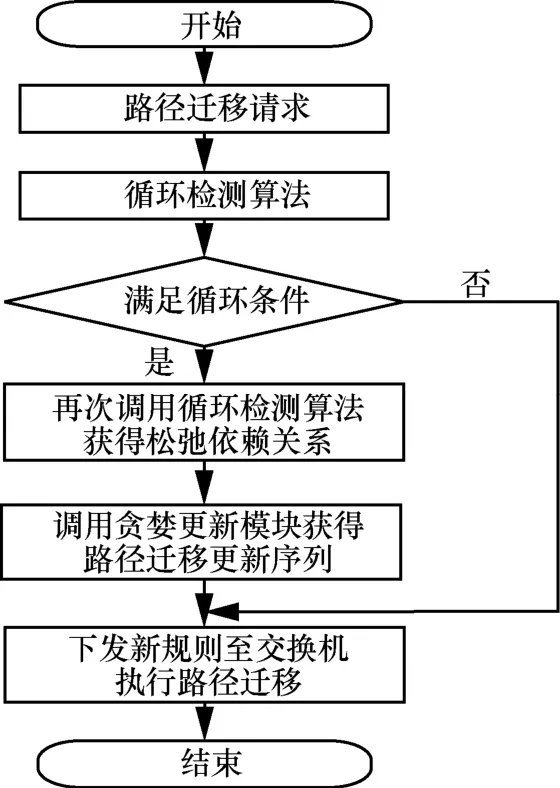
图2 快速无循环路径迁移流程

2.2 基于节点排序的快速循环检测算法

在实施路径迁移时，需要以有效的方式来检测迁移过程是否会发生循环，以避免数据包对链路带宽的无效重复占用。现有方案[7,11]均通过构建新旧路径之间的有向图并求解强连通分量来实现循环检测，多流处理时间开销较高。而本文所提快速循环检测算法NRLD 仅需通过对比相邻节点在新旧路径上的位置关系即可实现对循环的检测。检测步骤如下。

步骤1NRLD 按照流在旧路径上的传输顺序对各节点依次编号，获得节点编号集合seq_po，即

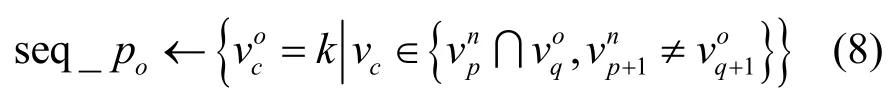
步骤2NRLD 根据新路径上流传输顺序获得新的编号顺序集合seq_pn，即

步骤3最后通过逐项比较新路径编号序列seq_pn中相邻节点编号值的大小即可在完成检测的同时输出循环位置loop_loc，即

基于节点排序的快速循环检测算法示例如图3所示。图3 中，新旧路径拓扑一共包含7 个公共节点，起始节点为v1，终止节点为v7。首先根据步骤1 获得旧路径节点编号seq _po为[1-7]。然后根据步骤 2 获得新路径相对应的节点编号seq _pn为[1,4,3,2,6,5,7]。最后，通过对比seq _pn中相邻节点的编号大小，可知新旧路径存在循环且可能发生循环的位置为[4,3,2]和[6,5]。

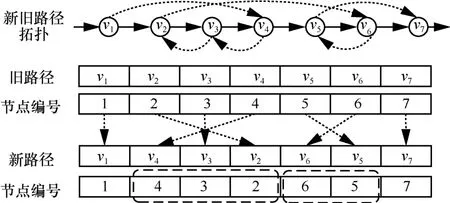
图3 基于节点排序的快速循环检测算法示例

NRLD 伪代码如算法1 所示。

算法1基于节点排序的快速循环检测算法

输入新路径pn，旧路径po

输出节点循环关系loop_loc

2.3 基于节点排序的松弛依赖关系检测

为便于理解，在介绍具体算法之前先给出节点依赖关系相关定义并证明相关结论。

定义3节点依赖性。如果节点在节点之前更新，将导致之间产生循环，称节点vn依赖于节点vm，表示为vn＜vm。

已有方法通过搜索有向图中的强连通分量可找到节点之间满足的依赖关系。需要说明的是，求解强连通分量获得的是节点之间的强依赖关系。强依赖关系定义如下。

定义4强依赖关系。在任意更新轮ui中，节点vn必须在节点vm之前完成更新以避免循环，称vn和vm之间满足强依赖关系。

强依赖关系表现在有向图中即存在从节点vn指向节点vm的与旧路径po相反的有向边。以图1为例，通过求解可知为新旧路径组成的有向图中的一个强连通分量。因此，根据定义4，节点集须按照顺序逐个进行更新。现有工作已经证明了根据强依赖关系进行节点更新可以避免循环[7]。

事实上，尽管基于强连通分量以及强依赖关系进行节点更新保证了严格避免循环，但更新时间因此将同时受到有向图规模以及依赖链长度的严重影响。同时，通过观察发现，在一定条件下，满足强依赖关系的节点可同时更新而不造成循环。如图1所示，如果交换机v1先更新将消除 [v2,v3]之间存在的强依赖关系而使之可以实现同时更新。本文称这种更新关系为松弛依赖关系，定义如下。

定义5松弛依赖关系。在新旧路径组成的有向图Gd中，节点vn的更新将使节点集Vr=中任意节点所具有的强依赖关系消失，称Vr中节点之间满足松弛依赖关系。其中，vn称为松弛依赖触发点，vm+1称为松弛依赖终止点。根据定义5 可得以下结论。

结论1松弛依赖触发点vn与其在新路径pn和旧路径po上的后继节点具有相同排列顺序。

证明假设松弛依赖触发点vn与其在新路径pn和旧路径po上的后继节点具有不同排列顺序，即在有向图中存在从节点vn出发的具有相反方向的2 条有向边，如图4 所示。此时，节点vn与其在旧路径上的直接祖先节点形成强连通分量。根据定义3，此时vn的更新依赖于将取代vn成为新的松弛依赖触发点。可知与前提假设矛盾，因此结论1 成立。证毕。

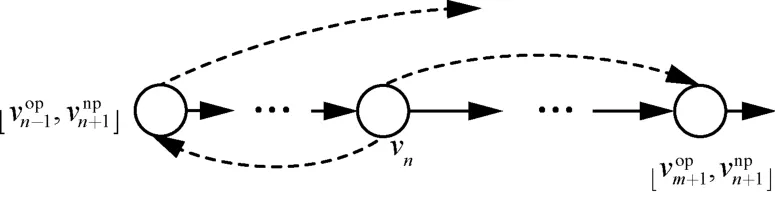
图4 结论1 参考示意

结论2 由vn触发松弛依赖的节点集Vr必包含在vn与其在新路径上的下一跳节点之间。

图5 结论2 参考示意

结论3松弛依赖节点集Vr内节点可同时更新且避免循环。

证明由转发唯一性（式(5)约束3）可知，松弛依赖触发点vn在同一时刻只能保留一条输出边用于流量转发。因此，vn在t时刻的更新将导致vn与其在旧路径po上下一跳节点之间不再存在有向边，如图6 所示。再由流守恒约束（式(7)约束5）可得，在vn更新后，vn与其在新路径上的下一跳节点之间的所有节点之间均不存在组成旧路径po的有向边。显然，此时vn与之间的节点可以同时更新而不违反循环依赖。同时根据结论2 可知，vn与之间的节点即满足松弛依赖的节点集Vr，故结论3 成立。证毕。

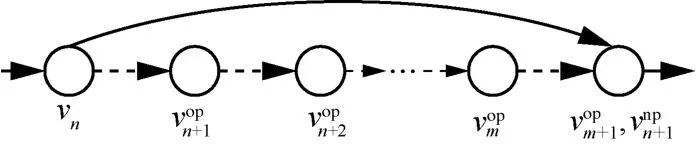
图6 结论3 参考示意

根据上述结论可知，并非所有待更新节点均可同时满足松弛依赖更新条件。因此，如何快速找到满足松弛依赖的节点集Vr成为进一步所关注的内容。通过分析发现，基于NRLD 同样可实现对松弛依赖关系的快速检测。不同之处在于，NRLD 步骤3中的相邻节点大小关系需进一步约束。

此时，满足松弛依赖的节点集为

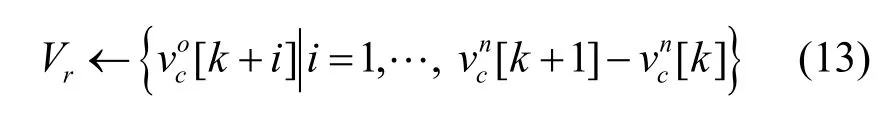
对于图3，新路径pn相邻节点编号[1,4]和[2,6]满足式(12)给出顺序递增关系。因此可知旧路径po节点集即满足松弛依赖的节点集。结合已有结论，给出并证明如下定理来说明算法有效性。

定理1基于NRLD 获得的松弛依赖关系进行路径迁移不产生任何循环。

由于松弛依赖关系检测与NRLD 仅在步骤3 的判别条件上存在差异，因此不再重复给出NRLD 伪代码。

2.4 贪婪更新算法

节点之间的松弛依赖关系本质上表征了节点实施并行更新的局部约束条件。因此，对松弛依赖集内的节点进行同步更新只能满足部分优化需求。为了进一步减少整体更新时间，需要提出一种更高效的更新调度机制，在每轮操作中更新更多的节点以减少控制器与交换机交互的次数，从而符合式(1)给出的目标函数。考虑2 种不同的更新方式。

方式1在每轮更新中选择可并行更新的最大数量松弛节点集

方式2在每轮更新中选择具有最多松弛节点的集合

然而，通过分析网络拓扑结构发现，单独执行二者中任意一个都无法满足优化目标。对于方式1，可能并不存在可并行更新的松弛节点集。如图7(a)所示，节点对 (v1,v4)和 (v2,v5)可分别导出松弛依赖集 [v2,v3]和 [v3,v4]。显然，二者存在重叠部分，即公共更新节点v3。因此，触发点v1和v2无法同时进行更新以导出松弛依赖集。原因在于，如果v2先完成更新，此时流的转发路径为v1→v2→v5。节点v3和v4上的转发规则可能会因为在有效时间内没有匹配数据包被超时删除。因此，当v1更新后，流的转发路径v1→v4→v5就会成为断路而导致丢包。

因此，结合上述示例，本文提出了贪婪更新机制RDGU。在每轮更新开始之前，RDGU 首先检测是否存在无重叠松弛依赖集。若存在，则根据可并行更新的松弛依赖集中节点数与中节点数的比较结果选择不同方式进行更新。

其中，方式1 更新流程如图7 所示，方式2 更新流程如图8 所示。当存在多个包含相同数量节点的Vr时，任意选择其中一个进行更新。

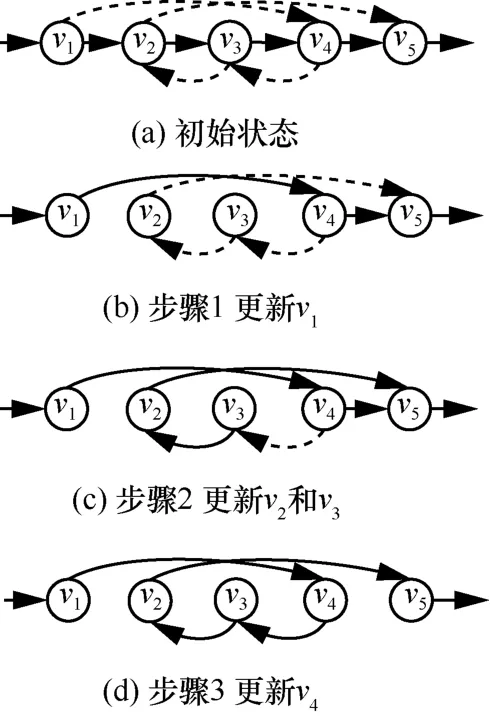
图7 方式1 的更新流程

本文给出并证明如下定理来说明RDGU的有效性。

定理2无重叠松弛依赖集中节点更新是相互独立的。

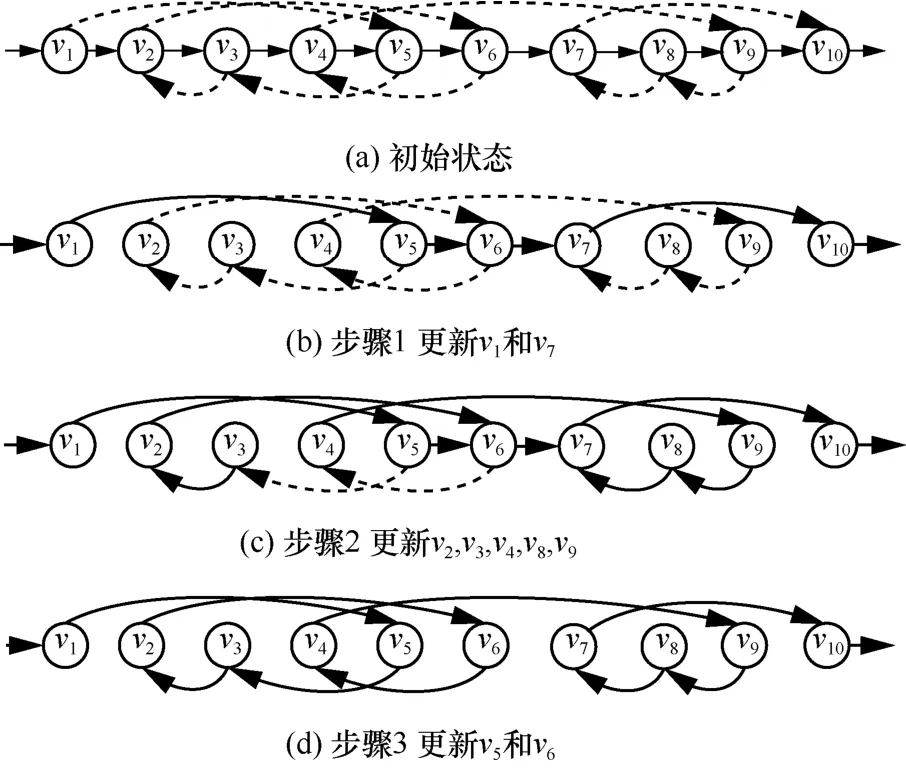
图8 方式2 的更新流程

定理3基于RDGU 算法进行节点更新不产生任何循环。

RDGU 伪代码如算法2 所示。

算法2基于松弛依赖关系的贪婪更新机制

2.5 时间复杂度分析

由于循环检测算法以及松弛依赖关系检测算法具有相同的执行过程，因此二者具有相同的时间复杂度。其中，节点编号可以O(1)的时间复杂度完成，相邻节点编号对比的时间复杂度为O(n)，n为新旧路径公共节点数量。因此，检测过程总的时间复杂度为O(n)。相比于求解强连通分量，检测过程不再需要遍历边。

对于贪婪更新机制，由于一个具有n个公共节点的有向图至少包括2 个松弛依赖集合，因此判断松弛依赖节点集中是否存在无重叠集合的时间复杂度为O(n2)。对于节点更新过程，最坏情况下需要n轮完成更新，即每次只更新单一节点。因此其时间复杂度为O(n)。综上可知，提出的贪婪算法的总体时间复杂度为O(n2)，且整体路径迁移算法的时间复杂度为 O (n2+n )～ O (n2)。

3 实验及分析

本节通过仿真实验验证了所提路径迁移机制的有效性并与已有的代表性方案进行了对比。

3.1 实验设置

实验环境。本文所有算法均在Ubuntu 18.04 LTS 环境中使用Python 3.8 编程实现。硬件配置为AMD Ryzen 7-4800H 处理器，16 GB 内存。

网络拓扑。使用了一个随机拓扑和取自The Internet Topology Zoo[12]2 个不同规模的真实网络拓扑来评估提出的算法：1) 随机拓扑，包括17 个节点和31 条边；2) GEANT2 拓扑，包括24 个节点和38 条边；3) INS-INC 拓扑，包括33 个节点和40 条边。实验拓扑如图9 所示。

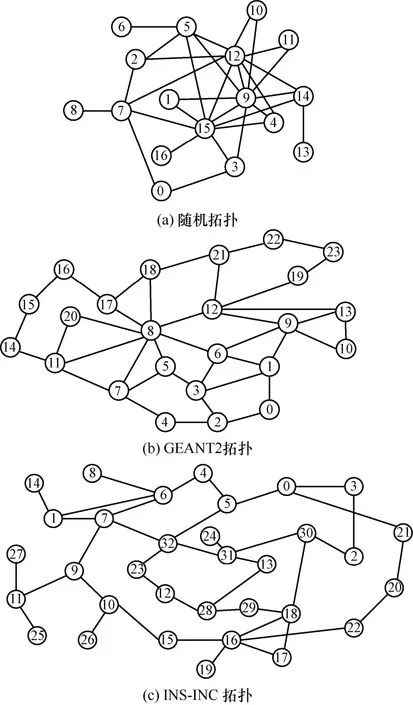
图9 实验拓扑

路径生成。从拓扑中随机选择节点来模拟流转发的源节点和目的节点。然后计算并选择节点之间的任意一条简单路径（不存在重复节点的路径）作为流转发的旧路径。进一步，随机排列旧路径上除源节点和目的节点之外的其他节点来构造出存在转发循环的新路径。

实验参数。考虑到典型的真实网络拓扑平均直径约为log(n)[13]，结合计算开销及实际情况（如生成树协议计时器的默认值将最大网络直径限制为7），实验中最大公共节点数量设为规则基准更新时间设为0.5 ms。同时考虑到规则更新时间受交换机性能如流表占用率、队列长度等指标影响，因此将该时间乘以[0,1)内的随机数来模拟真实规则更新时间。控制器到交换机的信道时延为0.5 ms。每组实验运行10 次取平均值保证无偏性。

3.2 循环检测算法性能对比及分析

首先验证所提NRLD 算法与已有算法在不同条件下对于循环的检测时间差异。为保证公平性，所有算法结果被转换为相同输出形式。对比算法如下。

深度优先搜索（DFS,depth-first search）。从源节点开始对新旧路径形成的有向图进行遍历。

Tarjan[7,11]。通过寻找强连通分量，发现有向图中存在的环路。

不同的循环检测算法在不同更新路径数量下的循环检测时间对比如图10 所示，其中新旧路径的公共节点数设置为6，包括源节点和目的节点。

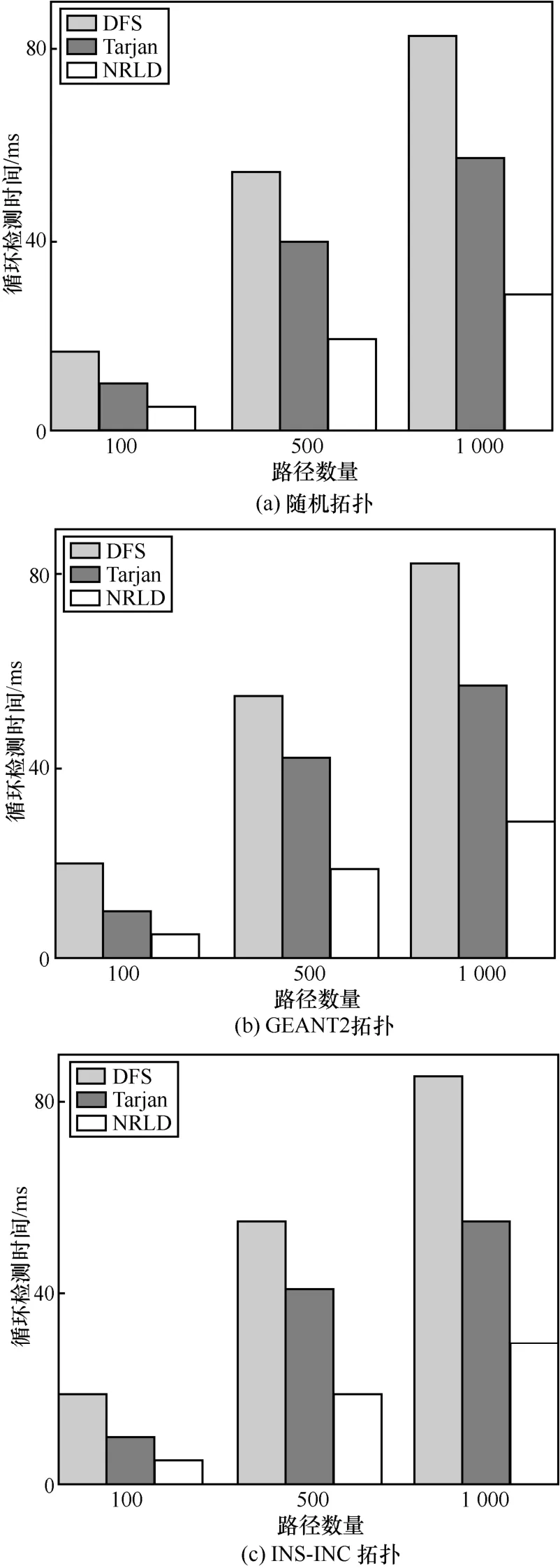
图10 不同更新路径数量下的循环检测时间对比

从图10 中可以看出，NRLD 在不同拓扑上均取得了最佳性能。这里以GEANT2 拓扑上路径数为500 时的结果为例来进行分析。对于DFS 和Tarjan，NRLD 可将检测时间分别减少64.58%和55.81%。原因在于，一方面，NRLD 是通过对比相邻节点的序号来进行循环检测的，避免了DFS 和Tarjan 在循环检测过程中基于堆栈的节点逐项对比操作。另一方面，DFS 对有向图遍历的输出结果为有向边的形式，需要更多时间将输出结果处理为节点之间的依赖关系。而Tarjan 所涉及的退栈以及修改时间戳操作影响了其检测性能。

不同的循环检测算法在不同公共节点数量下的循环检测时间对比如图11 所示，其中路径数量设为 500。根据前文所述，实验中随机拓扑、GEANT2拓扑和INS-INC拓扑的最大公共节点分别为7、9、10。从图11 中可以看出，在给定的节点数量范围内，NRLD 在3 个不同的拓扑上均获得最小的检测时间。特别地，当公共节点数量越多时，NRLD 优势更加明显。例如，在GEANT2 拓扑上，相比于DFS 和Tarjan，当节点数量为6 时，NRLD将检测时间分别减少了34.41 ms 和19.35 ms；当节点数量为9 时，NRLD 将检测时间分别减少了82.98 ms 和29.89 ms。产生这一现象的主要原因是当公共节点数量增多时，新旧路径之间形成循环的数量将同步增加，这将导致DFS 和Tarjan 产生更多的入栈以及退栈操作。而每次入栈后的节点逐项对比又进一步增加了时间开销。注意到，3 种算法的检测时间增长均呈现非线性趋势。这也对具有低时延需求的相关路径优化方案（如多路径转发）以及故障恢复策略带来了一定的启发，即新旧路径应尽可能地避免重叠。

3.3 整体方案性能对比及分析

本节进一步验证提出的路径迁移策略整体性能与已有迁移更新方案在多项指标上的差异。对比方案如下所示。

CCG[10]。对满足循环依赖的节点逐个进行倒序更新。

Cupid[7]/FCFU[2]。将节点集分割为不存在依赖关系的更新片段并在段内施行倒序更新。

RU[11]。在Cupid/ FCFU 基础上，段内的第一个循环节点最后更新，其余节点同步更新。

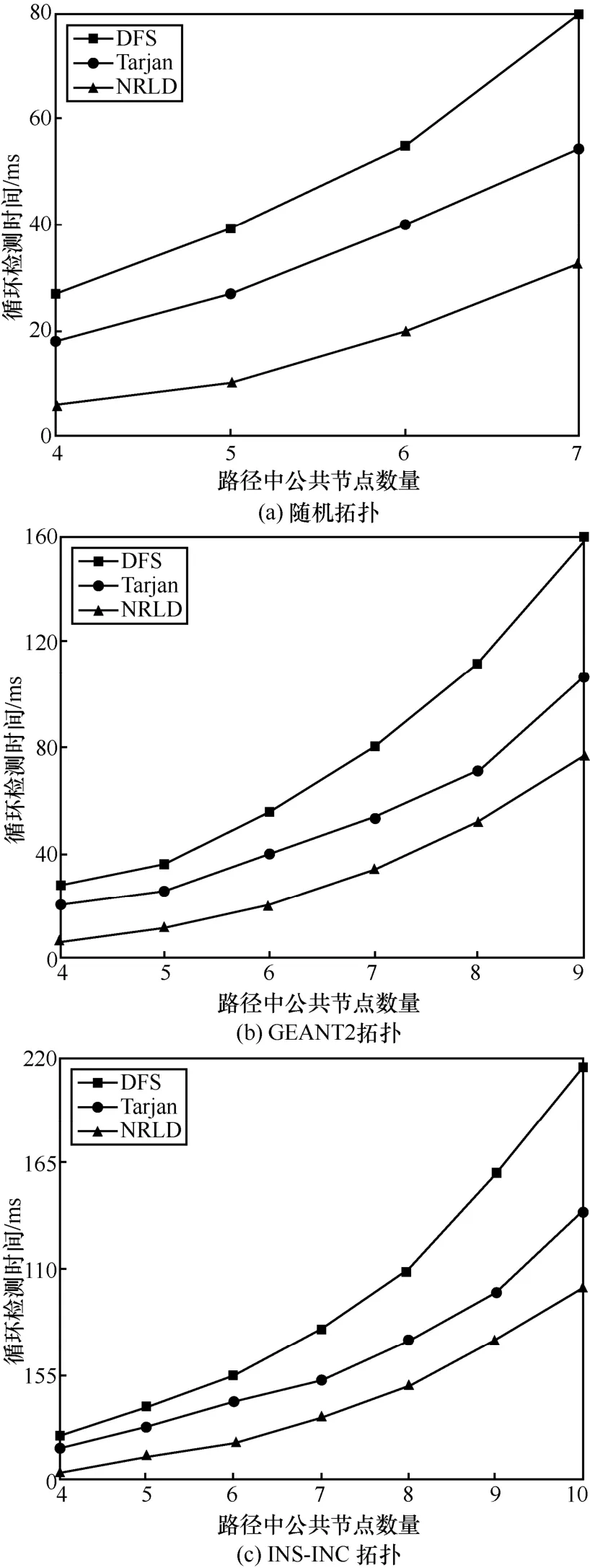
图11 不同公共节点数量下的循环检测时间对比

首先在不考虑循环检测时间的情况下，验证了提出的基于贪婪算法的更新机制相比于上述方案的优势。各方案在不同公共节点数量下的平均归一化路径迁移更新时间对比如图12 所示，其中更新路径数量设为500。为更好地体现方案之间的性能差异，将实验结果以CCG 为基准进行归一化。当公共节点数量为4 时，所有算法的更新时间相同。这是因为此时新旧路径只存在单一形式的循环，并不满足松弛依赖以及并行更新执行的条件。而当公共节点数量逐渐增加时，所提更新机制的优势开始显现，而且随着节点数量的增加，其性能优势更加明显。例如，在GEANT2 拓扑上，相比于其他方案，所提贪婪更新机制在公共节点数为6 时分别降低了17.5%和7.5%（Cupid/FCFU和RU 在此时的时间开销是相同的）的时间开销。而当公共节点数为9 时分别降低了54.8%、17.8%和14.7%。这是因为当公共节点数量较多时，新旧路径之间开始出现较长的松弛依赖节点集以及并行集。这些集合使所提算法可以在更少的轮数内完成节点更新。

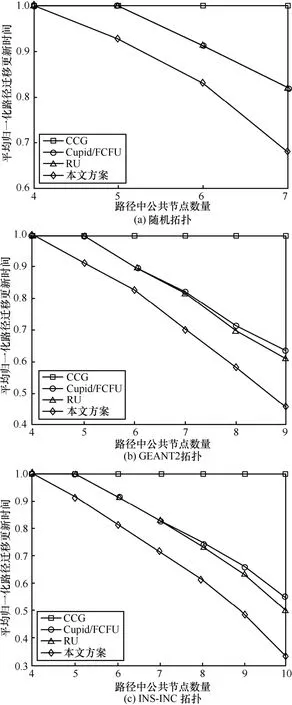
图12 不同公共节点数量下的平均归一化路径迁移更新时间对比（更新路径数为500）

需要说明的是，当公共节点数量不超过7 时（图12(a)所示），Cupid/FCFU 和RU 两类算法的更新时间是一致的。这是因为此时新旧路径形成的循环中的更新片段并不存在可同步更新的节点。因此RU 算法退化为与Cupid/FCFU 算法一致。而当公共节点数量超过7 时，RU 算法展现出了一定的优势。

进一步，各方案在不同更新完成时间下的路径迁移更新完成率如图13 所示。

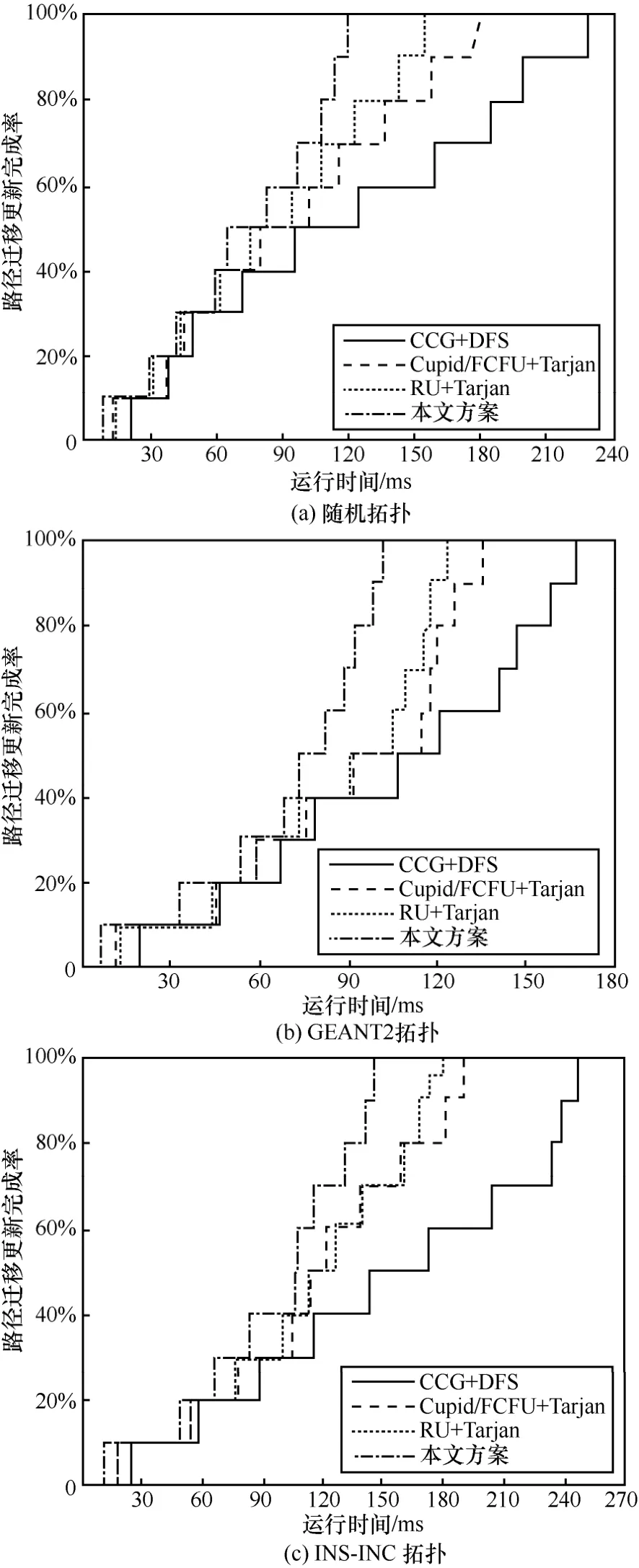
图13 不同更新完成时间下的路径迁移更新完成率（更新路径数为100）

对于CCG 算法，使用了DFS 来检测其循环。而Cupid/FCFU 和RU 则按照原文献描述均使用了Tarjan 来求解强连通分量。对于本文所提出的贪婪更新机制，则使用NRLD 来检测节点松弛依赖关系。实验中更新路径数量设定为100 且其中公共节点数的比例如表2 所示。同时，规定单一交换机上规则更新是逐个进行的。从图13 中可以看出，算法运行前期4 种方案在不同拓扑上的路径迁移完成率相差不大。随着运行时间的增加，本文方案展现出了明显的优势。这主要是因为在运行前期完成更新的均为较短路径，即公共节点数较少的路径。因此4 种方案的性能差异仅表现在循环检测时间上。在运行后期，长路径的迁移需要CCG、Cupid/FCFU和RU 运行更多的轮数。而本文方案得益于长路径节点之间普遍存在的松弛依赖关系以及贪婪更新机制，因此可在同一轮中更新更多的节点。更少的更新轮数意味着更少的更新时间。同时，该实验结果也表明，当网络面临由于链路故障而导致的大量路径并发迁移需求时，本文更新机制同样也可具有快速收敛性能。这是由于一方面，本文机制并不依赖于网络状态，而只与网络规模有关；另一方面，不同流之间的迁移过程在循环检测和更新策略的计算中并不存在依赖关系。因此迁移过程类似于流水线操作，先完成迁移计算的流可以先执行迁移。

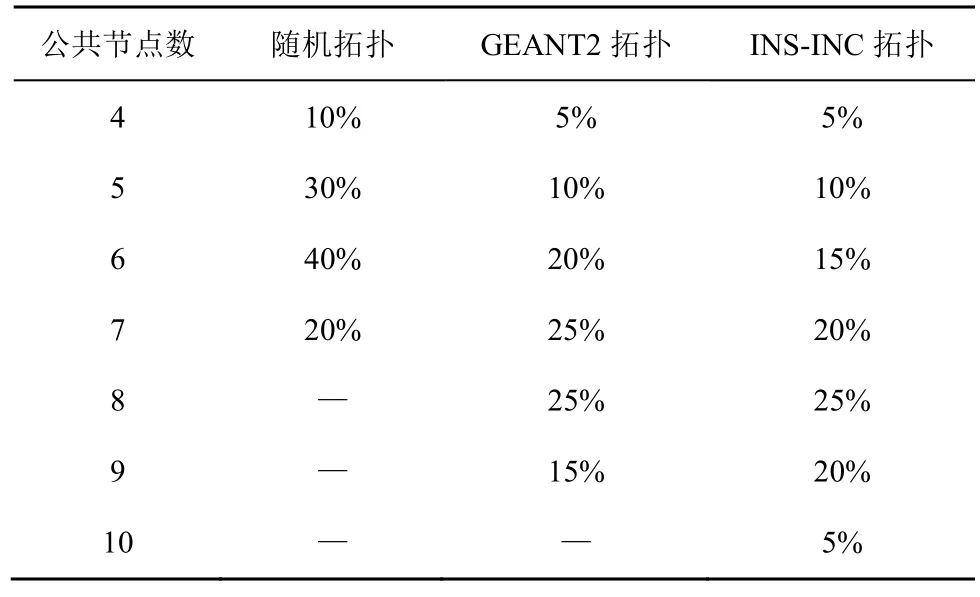
表2 3 种拓扑中不同公共节点的路径比例

4 结束语

本文对软件定义网络架构下的流路径迁移缓慢及故障等问题进行了研究，提出了一种快速无循环路径迁移策略。该策略首先基于节点排序实现了路径循环的快速检测。在此基础上，通过发掘节点之间的松弛依赖关系并构建贪婪更新机制，保证了节点更新过程的快速实施。仿真结果表明，相比于现有路径迁移机制，本文所提策略在保证路径迁移无循环的前提下，实现了更快的检测及迁移速度，且在不同拓扑及网络条件下均具有良好的稳定性。即使面临网络链路故障导致的大量并发路径迁移操作，同样具有较好的收敛性。