城市超小半径隧道沿程阻力系数研究
高 峰,何 江,冉 飞,贾 山,尹定鹏
(1.重庆交通大学 土木工程学院,重庆 400074;2.中国建筑第八工程局有限公司,上海 200135)
0 引言
城市地下交通联系隧道,简称UTLT,即Urban Transport Link Tunnel,主要修建于城市核心商务区域,是一种新兴的城市市政交通工程。该类工程具有平面曲线半径小、纵坡率大的特点,并且隧道内车流量大,车速较低。这些特点带来了更高要求的通风标准和新的通风问题。
现阶段关于城市地下交通隧道的研究主要集中在运营通风的防火排烟上;针对其沿程阻力系数的研究还较少。王峰[1]针对曲线隧道的不同半径、风速、壁面粗糙度等因素进行了沿程阻力系数影响分析,最后得到了曲线隧道的沿程阻力计算公式。李琼、陈超、袁浩庭[2-3]等针对长沙营盘口隧道进行物理模型试验,研究了多通道城市地下隧道主线与匝道之间的阻力损失与污染物扩散。CASCETIA[4]等通过三维数值模拟研究了隧道不同交通拥堵状况和压力损失之间的关系,提出了压力损失相关性函数,并表明相对于CFD模拟结果,新型相关性函数的平均百分比误差约3%。徐鹏辉[5]等完成了隧道排烟阻力的模型试验,分析排烟道因壁面粗糙度和缝隙漏风对沿程阻力系数的影响,研究得出了排烟道沿程阻力系数值的范围。
以上研究大部分是针对一般曲线隧道,关于城市超小半径隧道的沿程阻力系数研究较少,针对其独有的小半径和大纵坡特点的文献更少,有必要对此进行研究。
1 工程概况
渝中区解放碑地下车库和连接通道三期工程位于重庆市解放碑商圈,是重庆市、区两级重点基础设施工程。工程建设后将联通已完成的一、二期工程,形成地下“一环七线” 的交通循环,对改善区域内交通状况意义重大。
嘉滨路连接隧道(K0+000~K0+702.684)位于重庆市解放碑商圈地下,洞口西侧为居民楼,东侧紧邻洪崖洞景区;洞顶矗立110 KV高压电塔;规划线路范围分布有重庆市统战部、人防控制区、重医附二院、国泰艺术中心、地王广场、都市广场等18个重要的政府、军事、医疗机构,以及商业、住宅区域,实施过程中影响因素多、安全风险高。其为螺旋状的上中下3层结构,隧道当量直径为7.02 m,隧道断面和整体布局如图1所示。
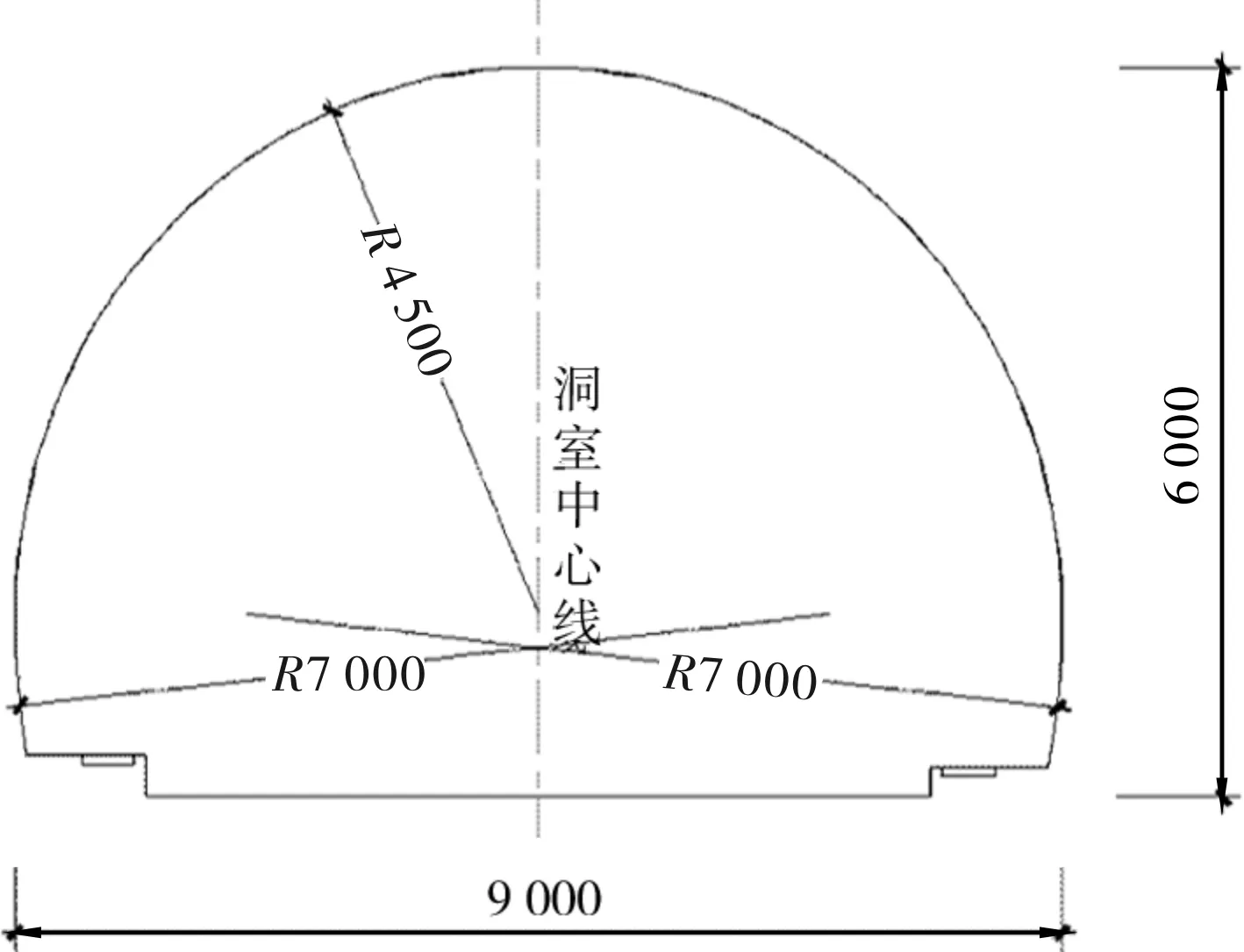
(a) 隧道横断面图(单位:mm)
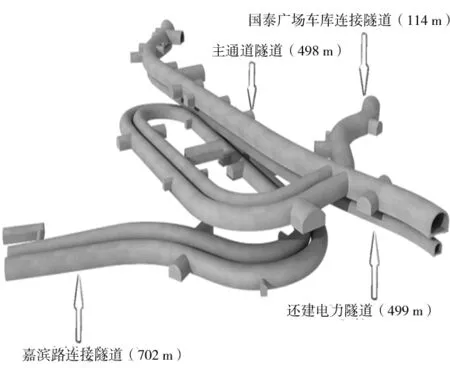
(b) 隧道相互位置图
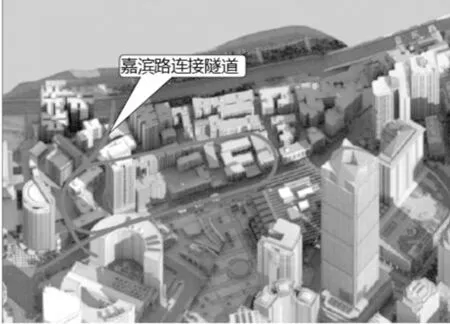
(c) 隧道位置三维图
2 计算模型
2.1 计算理论
2.1.1基本假定:
a.运营通风气流为低速连续介质,将其视为三维黏性不可压缩气流[6]。
b.通风视为非稳态紊流,考虑气流随时间的变化过程。
2.1.2控制方程:
采用处理器Fluent软件进行计算,因隧道内部气体流动属于湍流,选择标准k-epsilon双方程湍流模型[7]为计算数学模型,控制方程为连续性方程、动量方程。
连续性方程:
(1)
动量方程:

(2)
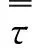
标准k-epsilon模型:
标准k-epsilon模型是普遍应用于数值计算中的一种计算模型,它适用于完全湍流状态下的流体的数值模拟。[8]标准k-ε模型的湍动能k和耗散率ε方程为如下形式:

ρε-YM
(3)
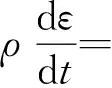
(4)

2.2 几何模型
以嘉滨路连接隧道实际尺寸为参考,建立隧道模型进行数值模拟。针对不同平面曲线半径和不同纵坡这2个研究对象,以ICEM CFD进行网格划分,Fluent作为求解器建立三维模型。数值模型的基本参数为:隧道横断面半径为7.02 m,圆心距离地面1.5 m;隧道平面曲线半径范围为30~200m,纵坡范围为0%~10%。隧道模型如图2所示。
2.3 边界条件
a.隧道入口为速度边界,类型为velocity-in-let,方向沿入口边界法线方向。
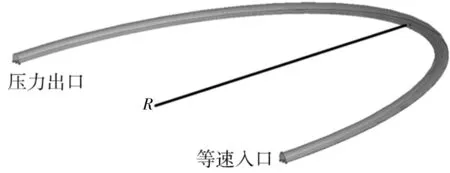
图2 隧道模型图Figure 2 Model diagram of tunnel
b.隧道出口为压力边界,类型为pressure-outlet,相对压差为0。
c.隧道路面和隧道内壁边界类型均为wall,满足无滑移条件,即Vi=0 m/s。
3 结果分析
3.1 数值模拟方法验证
为验证对计算超小半径隧道沿程阻力损失所采用的数值计算模型和方法的正确性,本文首先对不同长度的直线隧道和不同半径的曲线隧道进行数值模拟计算,并将其计算结果与规范公式进行比对。其结果如表1和表2所示。
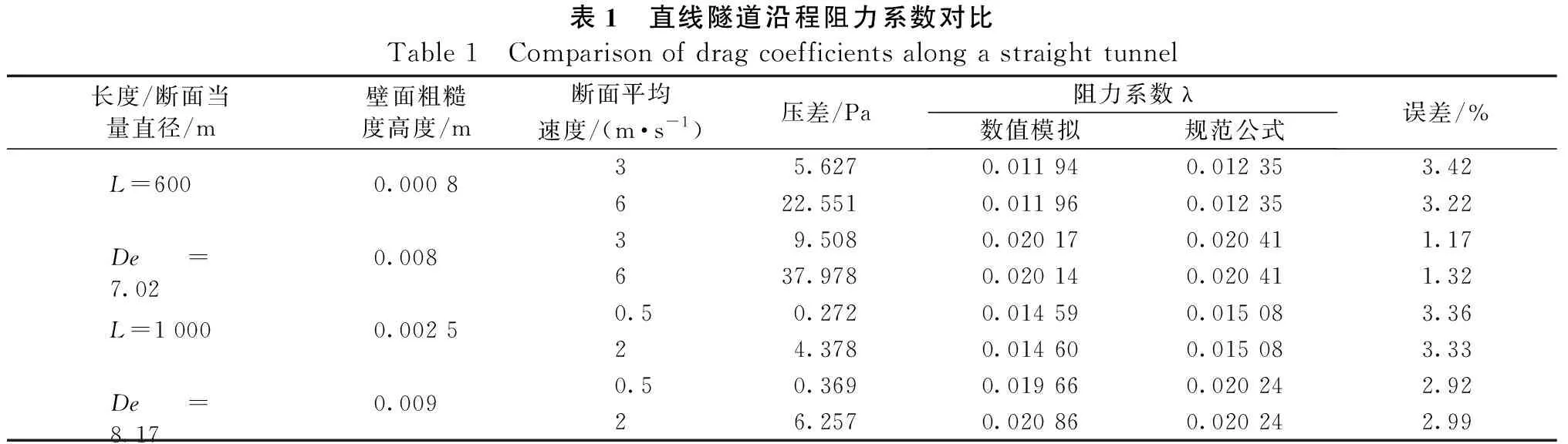
表1 直线隧道沿程阻力系数对比Table 1 Comparison of drag coefficients along a straight tunnel长度/断面当量直径/m壁面粗糙度高度/m断面平均速度/(m·s-1)压差/Pa阻力系数λ数值模拟规范公式误差/%L=6000.000 835.6270.011 940.012 353.42622.5510.011 960.012 353.22De=7.020.00839.5080.020 170.020 411.17637.9780.020 140.020 411.32L=1 0000.002 50.50.2720.014 590.015 083.3624.3780.014 600.015 083.33De=8.170.0090.50.3690.019 660.020 242.9226.2570.020 860.020 242.99

表2 曲线隧道沿程阻力系数对比Table 2 Comparison of drag coefficients along a curve tunnel长度/断面当量直径/m壁面粗糙度高度/m断面平均速度/(m·s-1)压差/Pa阻力系数λ数值模拟规范公式误差/%R=600L=1 1840.000 8319.6850.013 290.013 672.74678.8790.013 320.013 672.57De=7.02 0.008333.8400.022 850.022 601.146135.100.022 810.022 600.95R=1 000L=3 1400.002 50.50.9230.015 670.016 052.35214.7620.015 660.016 052.39De=8.17 0.0090.51.2370.021 010.021 532.43219.7890.021 000.021 532.46
由表1和表2的计算结果可以看出:①直线隧道的三维数值计算结果与规范公式计算结果基本吻合,断面平均风速对沿程阻力系数基本没有影响。②随着壁面粗糙度的增加,沿程阻力系数也逐渐增加。③隧道长度与沿程阻力系数无关。④曲线隧道沿程阻力系数与平面曲线半径有关,粗糙度相同,半径越大,沿程阻力系数越小;半径相同,粗糙度越大,沿程阻力系数越大。
3.2 隧道曲线半径对沿程阻力系数的影响分析
在纵坡一定的情况下,隧道平面曲线半径是影响沿程阻力损失大小的重要因素,公路隧道通风设计规范中给出了曲线隧道沿程阻力系数计算公式,并表明半径越小,沿程阻力系数越大。但公式中的R取值范围应为:200 m≤R≤2 000 m。而小于200 m的曲线隧道是否还适用于此公式,需要进一步研究。
本文选取了粗糙度为0.8 mm和8 mm的2种不同工况下,解放碑地下环道嘉滨路连接隧道的标准横断面隧道在平面半径为30~2 000 m的模型。分别计算了其沿程阻力系数。得出结果绘制对比图如图3和图4所示。
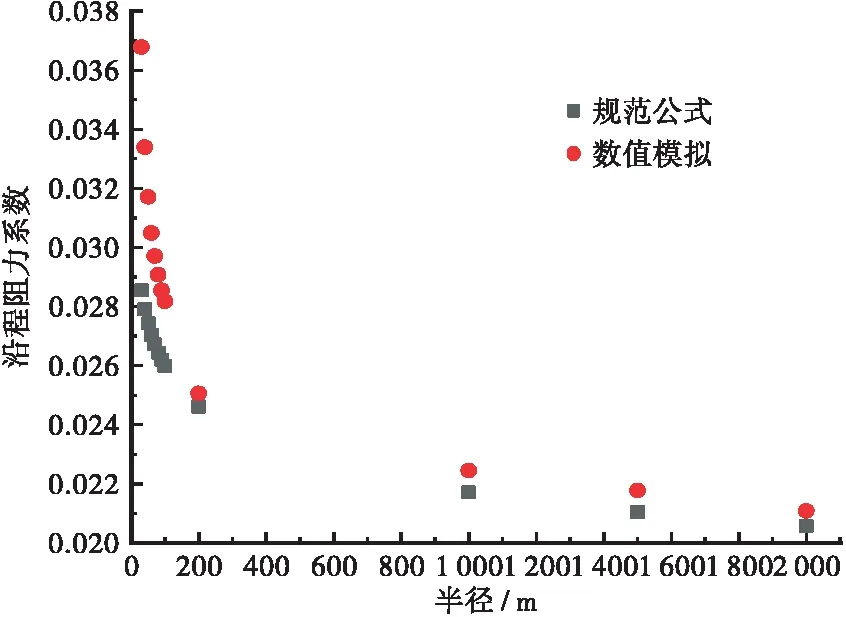
图3 不同半径下隧道沿程阻力系数变化(Δ=8 mm)Figure 3 Variation of drag coefficient along the tunnel under different radius(Δ=8 mm)
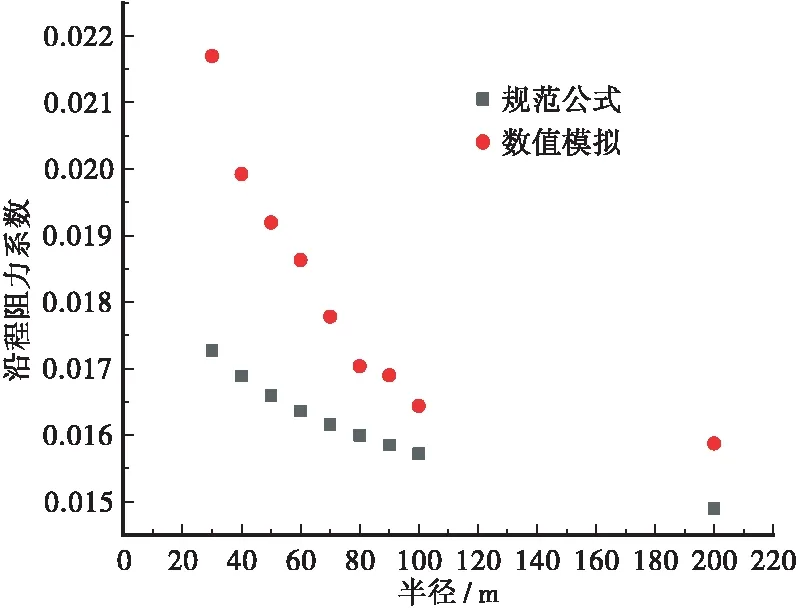
图4 不同半径下隧道沿程阻力系数变化(Δ=0.8 mm)Figure 4 Variation of drag coefficient along the tunnel under different radius(Δ=0.8 mm)
从图3和图4可以看出,曲线隧道的半径对沿程阻力系数的影响非常大。一般公路隧道的平面曲线半径在200~2 000 m之间,但城市地下隧道由于地形等限制原因,其曲线半径会小于200 m。由于《公路隧道通风设计细则》[9]中针对沿程阻力系数计算的公式是基于普通大半径隧道考虑的,因此在数值模拟过程中,可以清楚地看到,在平面曲线半径为200~2 000 m时,其沿程阻力系数与规范公式相差在误差范围内,均小于4%。但是在平面曲线半径小于200 m时,沿程阻力系数开始发生变化。
因此,在针对城市地下交通联系隧道进行通风设计时,一定要考虑因其半径过小而引起的沿程阻力系数变化,目前公路隧道通风设计规范在小半径工况下并不适用。
参考细则中提出的计算方法,对数值模拟中30~200 m范围数据进行非线性拟合,见图5、图6。

图5 不同半径下隧道沿程阻力系数拟合曲线(Δ=8 mm)Figure 5 Fitting curve of drag coefficient along the tunnel under different radius(Δ=8 mm)
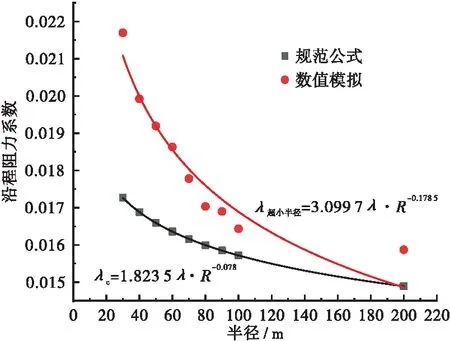
图6 不同半径下隧道沿程阻力系数拟合曲线(Δ=0.8 mm)Figure 6 Fitting curve of drag coefficient along the tunnel under different radius(Δ=0.8 mm)
根据数值模拟计算结果的非线性拟合(图5、图6)可得到如下公式:

(5)
式中:λ超小半径为超小半径隧道沿程阻力系数;λ为直线隧道沿程阻力系数;R为隧道平面曲线半径(30~200 m)。
对拟合公式进行反算,可以发现结果与数值模拟绝大多数值重合。
探究城市超小半径沿程阻力系数增大的原因,可从内部风速矢量分布来进行分析,如图7所示。

(a)R=30

(b)R=60

(c)R=100

(d)R=200
图7是洞内弯道位置风速矢量曲线,通过矢量图可以看出,半径越大的隧道内风流矢量分布均匀,没有明显的气体分子不规则运动,且几乎紧贴隧道外凸侧壁运动。而随着半径的减小,隧道内的速度梯度分布逐渐变大,壁面切应力也随之变大,导致沿程阻力系数增加。同时靠近内凹侧的空气开始做不规则运动。外凸侧小部分气体分子也开始向内窜流,不规则紊流运动的分子数量逐渐增加。湍流运动中可以通过式(6)来计算湍流切应力。
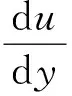
(6)

超小半径的城市地下隧道通风过程中沿程阻力系数增大的原因为2个方面:
a.从式(2)和隧道断面风速矢量图可以得到,随着半径减小,内部空气与隧道内凹壁间的速度梯度增大,切应力就随之增大,空气在隧道内流动的过程中损失的能量就变多了,沿程阻力损失就相应增大。
b.隧道壁面边界条件的弯曲变化导致隧道内空气运动逐渐变得不规则,气体的不规则运动会使流体之间的阻力变得更大,这是导致沿程阻力系数逐渐增大。
因此,在城市地下环道通风设计中,应该尽量避免隧道曲线半径过小;其次应该将隧道内壁粗糙度降低;在弯道位置采用合理的通风方式减少损失。
3.3 隧道纵坡变化对沿程阻力系数的影响分析
城市地下交通联系隧道纵坡比一般公路隧道要大很多。纵坡能对隧道内运营通风所需风量产生比较严重的影响。上升的坡度越陡,需要的风量就越大。而且隧道线型上升太陡会使汽车在隧道内产生更多的污染气体,给隧道内通风换气、火灾排烟等带来更多的问题。
表3和表4为直线段隧道和曲线段隧道在不同纵坡下的沿程阻力系数与规范公式的对比分析。
由表3和表4的计算结果可以清楚的看到,纵坡对沿程阻力系数的影响较小。只有在纵坡大于5%以后,沿程阻力系数才有较为明显的增加,但即使纵坡达到10%,其值误差率仅为8%左右,还应该考虑系统误差、网格质量等因素。因此,纵坡对沿程阻力损失的影响较小,纵坡的增加并不足以明显影响隧道内运营通风的效果。
提取不同纵坡下的隧道内中心线1.6 m高度风速,绘制曲线如图8所示。
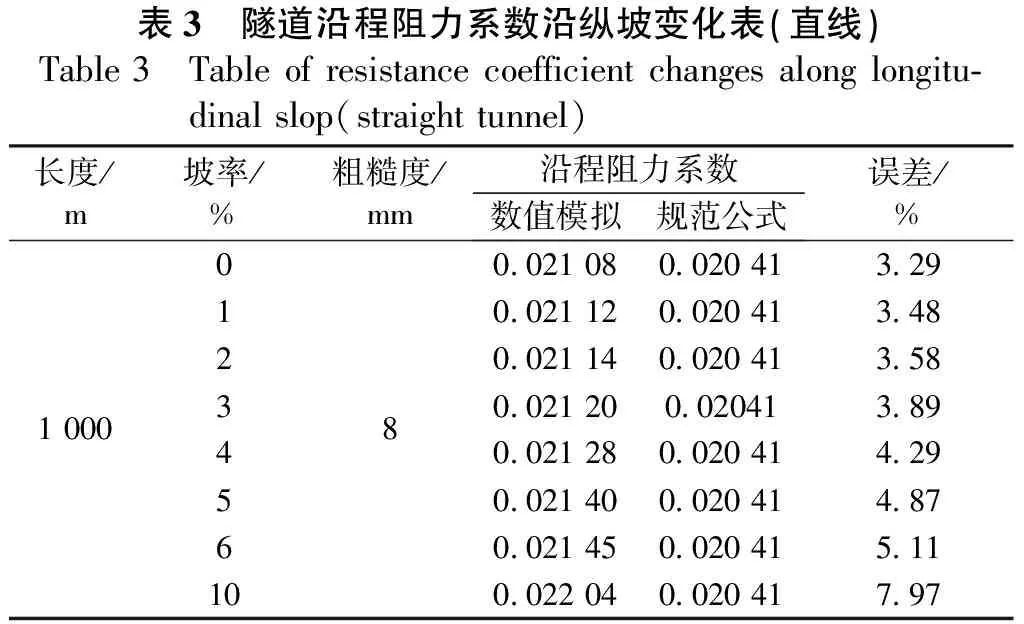
表3 隧道沿程阻力系数沿纵坡变化表(直线)Table 3 Table of resistance coefficient changes along longitu-dinal slop(straight tunnel)长度/m坡率/%粗糙度/mm沿程阻力系数数值模拟规范公式误差/%00.021 08 0.020 41 3.2910.021 12 0.020 41 3.4820.021 14 0.020 41 3.581 000380.021 20 0.02041 3.8940.021 28 0.020 41 4.2950.021 40 0.020 41 4.8760.021 45 0.020 41 5.11100.022 04 0.020 41 7.97

表4 隧道沿程阻力系数沿纵坡变化表(曲线)Table 4 Table of resistance coefficient changes along longitu-dinal slope(curve tunnel)半径/m坡率/%粗糙度/mm沿程阻力系数数值模拟规范公式误差/%00.026 22 0.025 35 3.4310.026 31 0.025 35 3.77200390.026 35 0.025 35 3.9250.026 51 0.025 35 4.5870.026 68 0.025 35 5.2400.028 18 0.027 51 2.4120.028 18 0.027 51 2.42100480.028 31 0.027 51 2.8960.028 60 0.027 51 3.9670.028 92 0.027 51 5.12
从速度折线图可以看出,无论隧道线型如何,内部前半程速度均在增加,后半程风速基本保持一致。隧道进出口速度差没有随着纵坡的增加而发生明显地改变,即无论纵坡如何,隧道内风速梯度是基本保持一致的,这就表明分子间切应力没有明显变化,沿程阻力损失不会发生很大的增长。
因此在城市地下交通的设计中,纵坡率在满足机动车动力要求和隧道内排水要求的条件下,对通风的影响比较小,在通风设计中,按照纵坡为0%进行简化设计也可以达到运营通风要求。
结合以上规律可知,隧道内沿程阻力系数受隧道平面曲线半径、隧道内部壁面粗糙度的影响较大,而风速、纵坡等因素不会造成太大的风能损失。在进行城市地下交通隧道的设计时,应该充分考虑到半径对通风的影响,尽可能避免设置超小半径的隧道。在无法改变隧道半径的时候,应该在弯道位置增设射流风机以加大通风功率,抵消弯道带来的损耗。
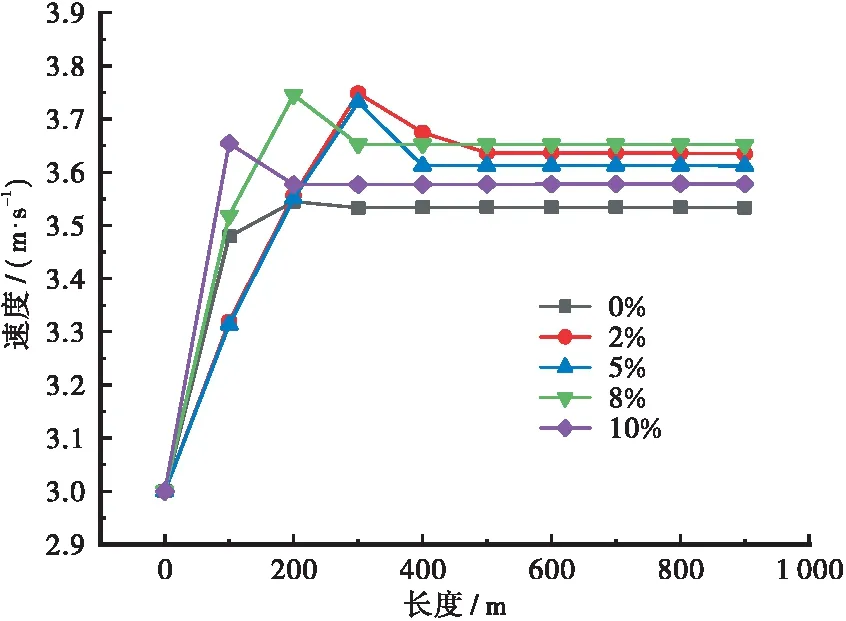
(a) 直线隧道中心线1.6 m高度处风速曲线图
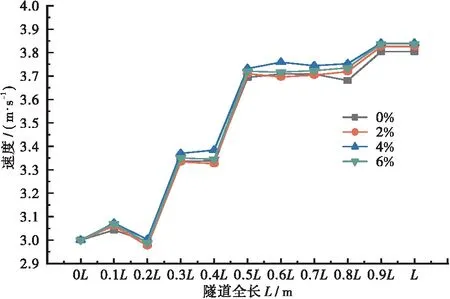
(b) 曲线隧道(R=100 m)中心线1.6 m高度处风速曲线图
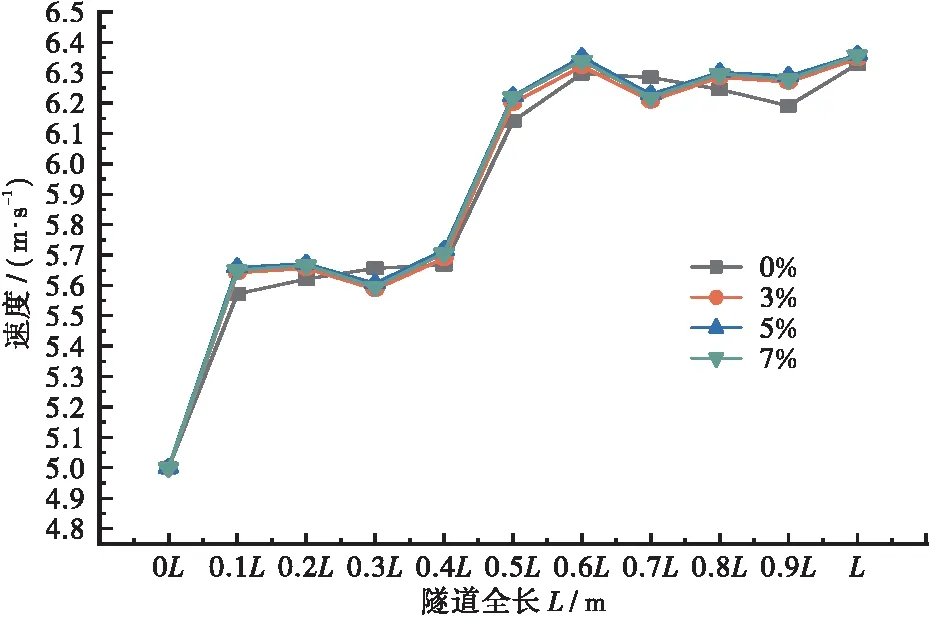
(c) 曲线隧道(R=200 m)中心线1.6 m高度处风速曲线图
4 结论
通过以上研究,得到以下结论:
a.现行公路隧道通风设计细则中使用的曲线隧道沿程阻力计算公式适用范围在半径200~2 000 m内。城市超小半径隧道的沿程阻力系数不能采用该公式计算。
b.针对城市超小半径隧道的沿程阻力计算方法进行了优化,得到如下公式:λ超小半径=3.099 7· λ·R-0.178 5;适用半径为:R=30~200 m。
c.城市地下隧道的大纵坡对沿程阻力系数影响较小,通风设计时可不用考虑纵坡带来的损失。

