大跨度PC连续梁桥预应力损失影响研究

毛德均， 余文正， 许 鹏， 陈 旭， 王春华

(1.昆明学院 建筑工程学院， 云南 昆明 650214； 2.云南通衢工程检测有限公司， 云南 昆明 650041)

0 引言

大跨度PC连续梁桥，常见形式主要为墩梁固结连续刚构桥和墩梁铰接连续梁桥，因具有受力性能好、跨越能力大、行车舒适、施工方便、工程造价低等优点，在我国交通基础设施建设中得到了广泛应用[1-3]。其主梁作为两向或三向预应力混凝土结构，预应力钢筋配置种类多、数量大。由于施工时张拉不到位、混凝土弹性压缩、锚具变形、管道摩阻力、预应力筋应力松弛或混凝土收缩徐变等原因，均会造成预应力损失，进而对成桥之后主梁的内力和变形造成影响。研究表明，纵向预应力损失是导致大跨度PC连续梁桥后期结构特性劣化和主梁出现下挠、开裂病害的重要原因，目前对其发生位置和损失程度难以做到准确预测，影响也难以做到定量判断[4-8]。

张宏祥[8]等以某五跨连续刚构桥为背景，采用有限元计算方法研究了纵向预应力整体发生不同程度损失时对主梁腹板应力和其中的顶板束、底板束分别发生不同程度损失时对主梁刚度的影响，结果表明，随着预应力整体损失的加大，主梁腹板主拉应力不断增加，顶板束预应力损失对主梁刚度的降低影响比底板束显著。汪磊[9]采用MIDAS/CIVIL对某三跨PC连续刚构桥进行有限元分析，比较了纵向预应力钢束的顶板束、腹板束和底板束分别损失30%时对主梁应力和变形的影响，结果表明，顶板、底板钢束预应力损失对桥梁中跨跨中挠度和下缘压应力影响较大。袁卓亚[10]等通过有限元计算分析建立了结构有效预应力衰减引起长期挠度和混凝土收缩、徐变引起长期挠度的相关关系，结合影响矩阵原理提出了基于长期变形监测挠度数据识别连续刚构桥有效预应力的方法。黄海东[11]等提出了一种基于预应力损失识别的连续刚构桥内力计算方法。周建庭[12]等采用响应面法研究了施工因素、材料性能和环境条件的随机性对连续刚构桥预应力损失的影响。劳晓春[13]等基于某连续刚构桥的应变监测结果和预应力钢束的布置图分析，研究了预应力损失与预应力钢束长度之间的非线性变化关系。张开银[14]等利用某大跨PC连续梁桥施工过程中顶板束的应变实测数据，研究了孔道弯曲和管道偏差对预应力损失的影响。徐学斌[15]等采用MIDAS/CIVIL建立有限元模型，研究了连续刚构桥的顶、底板束张拉顺序对预应力损失影响。

通过既有成果的综述分析可以发现，相关人员主要采用有限元计算、理论分析和现场试验手段，对大跨度PC连续梁桥预应力(尤其是纵向预应力)损失关联课题开展了研究，取得了丰硕成果，但具体到采用有限元方法开展的预应力损失对桥梁性能影响研究方面，预应力损失工况和损失程度参数设置代表性不够，没有很好地反映出预应力损失程度与目标参数之间的关系规律。本文以某四跨PC连续梁桥为背景，采用MIDAS/CIVIL建立有限元分析模型，研究了纵向预应力损失对该桥一阶自振频率、主跨跨中挠度和下缘压应力的影响，模型预应力损失工况和损失程度参数的设置相对更加全面，作为对既有研究的补充，可为掌握该类桥梁的长期工作性能提供参考。

1 工程概况

某PC连续梁桥，主桥总长320m，跨径布置为(60+100+100+60)m，双向两车道，设计汽车荷载等级为公路Ⅰ级，人群荷载2.5kN/m2，桥面设3.0%双向纵坡。上部结构为单箱单室截面箱梁，梁顶宽12.5m，底宽7.0m；箱梁根部梁高、腹板厚度和底板厚度分别为5.6、0.6和0.7m，跨中梁高、腹板厚度和底板厚度分别为2.5、0.45和0.28m，底板上缘与底板下缘均按1.8次抛物线规律变化。主梁采用C50混凝土，采用悬臂浇注法施工。该桥箱梁典型横断面如图1所示。

(a)根部

(b)跨中

箱梁主要采用纵向、竖向双向预应力结构，在墩顶0#、1#块横隔板和底板处施加横向预应力。主桥箱梁纵向预应力钢筋采用公称直径d=15.24mm的低松弛钢绞线，抗拉强度标准值fpk=1860MPa，弹性模量Ep=1.95×105MPa，公称面积Ap=140mm2。全桥钢束数量共260束，其中，顶板束180束，底板束56束，腹板束24束。钢束张拉控制应力σcon=0.72fpk=1339.2MPa，张拉方式为两端张拉。除施工阶段张拉钢束外，在顶板和底板分别设置了4束备用钢束。

2 有限元模型

采用MIDAS/CIVIL2019建立有限元模型，对该桥上部结构进行计算分析，根据截面变化特点和施工顺序进行结构离散。分析模型如图2所示，共有114个梁单元，划分51个施工阶段模拟挂篮悬臂浇筑法施工。模型除各种施工阶段荷载和移动荷载外，还考虑了收缩徐变、基础不均匀沉降、系统温差、竖向温度梯度对主梁的影响。预应力损失模拟通过调整张拉力大小实现。

图2 MIDAS/CIVIL计算模型Figure 2 MIDAS/CIVIL computing model

本文只分析纵向预应力损失影响，计算工况设定为3种类型，详情见表1，在表1中，顶表示顶板预应力钢束，底表示底板预应力钢束，腹表示腹板预应力钢束。对于计算结果，主要提取桥梁一阶自振频率与荷载频遇组合下的主跨跨中下缘压应力、主跨跨中挠度进行分析。

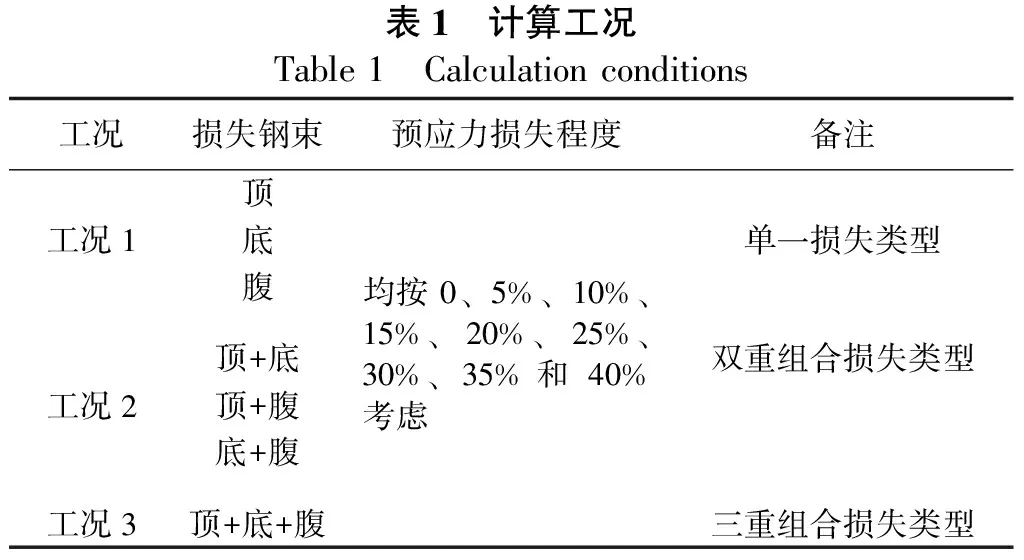
表1 计算工况Table 1 Calculation conditions工况损失钢束预应力损失程度备注顶工况1底单一损失类型腹均按0、5%、10%、15%、20%、25%、30%、35%和40%考虑顶+底双重组合损失类型工况2顶+腹底+腹工况3顶+底+腹三重组合损失类型

3 计算结果及分析

该桥上部主跨箱梁设计为全预应力混凝土结构，未发生任何损失时的计算结果为：桥梁主跨跨中下缘压应力σz=-9.4 MPa，主跨跨中挠度fl/2=-24.94 mm，桥梁一阶自振频率n=0.829 8 Hz。

3.1 工况1

工况1下，σz与预应力损失程度Yscd的关系曲线见图3，fl/2与Yscd的关系曲线见图4，n与Yscd的关系曲线见图5。以下和后续各图中，顶表示顶板预应力钢束，底表示底板预应力钢束，腹表示腹板预应力钢束。负数表示受压。

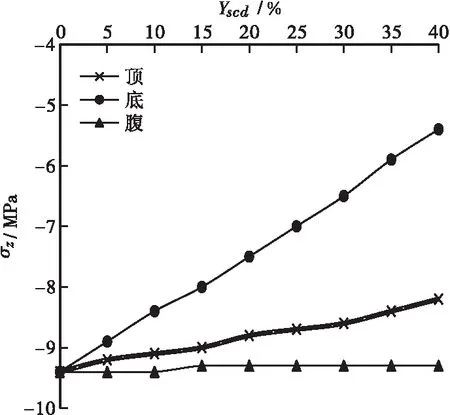
图3 σz-Yscd关系曲线(工况1)Figure 3 Relation curves of σz-Yscd(Condition 1)

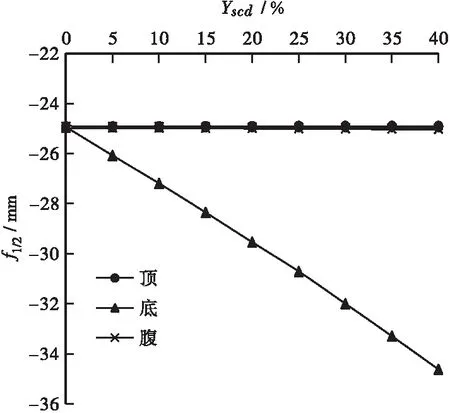
图4 fl/2-Yscd关系曲线(工况1)Figure 4 Relation curves of fl/2-Yscd(Condition 1)

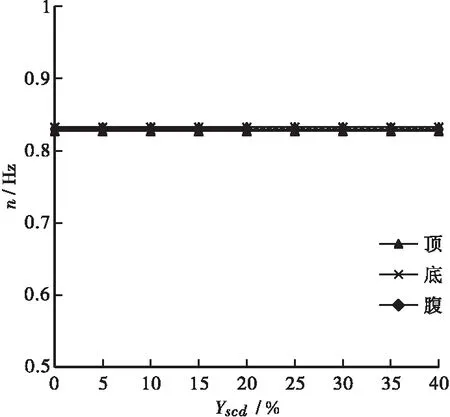
图5 n-Yscd关系曲线(工况1)Figure 5 Relation curves of n-Yscd(Condition 1)

由图3可知：底、顶、腹的σz-Yscd关系曲线均表现为线性变化规律，随着Yscd增大，σz均在减小，3种钢束的Yscd对σz的影响程度不同，底>顶>腹，当3种钢束的Yscd均达到40%时，σz分别为-5.4、-8.2和-9.3 MPa，σz相对于预应力未损失时的下降幅度分别为42.3%、12.8%和1.1%，说明σz受底板钢束预应力损失影响较大，受顶板钢束预应力损失影响较小，受腹板钢束预应力损失影响极小。

由图4可知：顶、底、腹的fl/2-Yscd关系曲线均表现为线性变化规律，其中，顶和腹的关系曲线基本重合且基本为水平直线，而底的则为斜直线，当Yscd均达到40%时，底对应的fl/2相对于未损失时增加了约-10 mm，而顶和腹对应的fl/2相对于未损失时的增加值均在-0.5 mm以内，表明fl/2受底板钢束预应力损失影响较大，受顶板和腹板钢束预应力损失影响极小。

由图5可知：顶、底、腹的n-Yscd关系曲线为水平直线且3条线重合，说明n基本不受顶板、底板或腹板钢束预应力损失影响。

以上结果表明，大跨度PC连续梁桥的纵向预应力钢束发生单一损失类型时，顶板、底板或腹板钢束预应力发生损失对桥梁主跨跨中下缘压应力和主跨跨中挠度的影响程度不同，而桥梁一阶自振频率则不受影响。

3.2 工况2

工况2下，σz与Yscd的关系曲线如图6所示，fl/2与Yscd的关系曲线见图7，n与Yscd的关系曲线见图8。

图6 σz-Yscd关系曲线(工况2)Figure 6 Relation curves of σz-Yscd(Condition 2)

图7 fl/2-Yscd关系曲线(工况2)Figure 7 Relation curves of fl/2-Yscd(Condition 2)

图8 n-Yscd关系曲线(工况2)Figure 8 Relation curves of n-Yscd(Condition 2)

由图6可知：顶+底、顶+腹、底+腹的σz-Yscd关系曲线均表现为线性变化规律，随着Yscd增大，σz均在减小，3种双重组合损失对σz的影响程度不同，顶+底>底+腹>顶+腹，当三者的Yscd均达到40%时，σz分别为-4.3、-5.4和-8.2 MPa，σz相对于预应力未损失时的下降幅度分别为54.3%、42.3%和12.8%，说明σz受顶+底预应力损失影响很大，受底+腹预应力损失影响较大，受顶+腹预应力损失影响较小。

由图7可知：顶+底、底+腹、顶+腹的fl/2-Yscd关系曲线均表现为线性变化规律，顶+底和底+腹均为斜直线且基本重合，而顶+腹基本为水平线，当Yscd均达到40%时，顶+底和底+腹对应的fl/2相对于未损失时均增加了约-10.5 mm，而顶+腹对应的fl/2相对于未损失时的增加值在-0.5 mm以内，表明fl/2受顶+底和底+腹预应力损失影响均较大，受顶+腹预应力损失影响极小。

由图8可知：顶+底、底+腹、顶+腹的n-Yscd关系曲线均为水平直线且3条线重合，说明n基本不受顶+底、底+腹、顶+腹3种双重组合预应力损失影响。

以上结果表明，大跨度PC连续梁桥的纵向预应力钢束发生双重组合损失类型时，顶+底、底+腹、顶+腹钢束预应力损失对桥梁主跨跨中下缘压应力和主跨跨中挠度的影响程度不同，而桥梁一阶自振频率则不受影响。

3.3 工况3

工况3下，σz与Yscd的关系曲线见图9，fl/2与Yscd的关系曲线见图10，n与Yscd的关系曲线见图11。

图9 σz-Yscd关系曲线(工况3)Figure 9 Relation curves of σz-Yscd(Condition 3)

图10 fl/2-Yscd关系曲线(工况3)Figure 10 Relation curves of fl/2-Yscd(Condition 3)

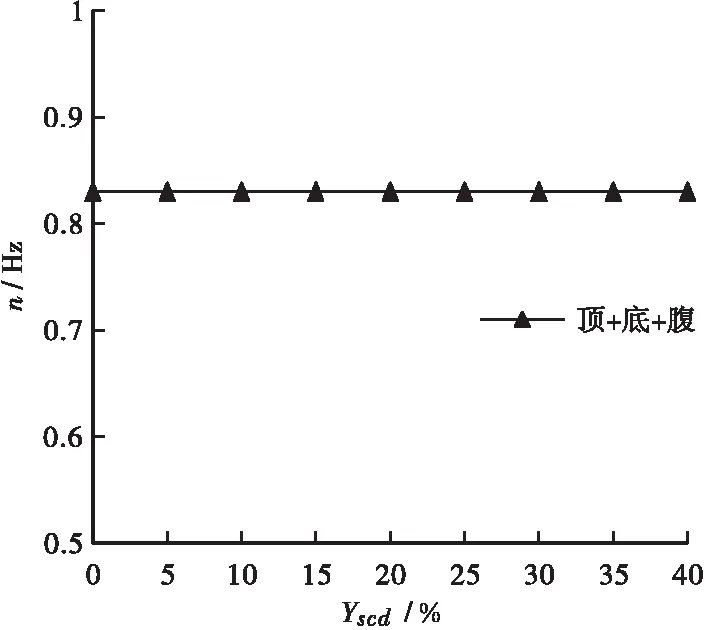
图11 n-Yscd关系曲线(工况3)Figure 11 Relation curves of n-Yscd(Condition 3)

由图9～图11可知：在工况3下，σz-Yscd和fl/2-Yscd关系曲线均表现为线性变化规律，随着Yscd增大，σz在减小，fl/2在逐渐增大，n-Yscd关系曲线为水平直线，当Yscd均达到40%时，σz相对于预应力未损失时的下降幅度为55.3%，fl/2相对于未损失时增加了约-11 mm，而n无明显变化。

3.4 综合分析

将3种工况计算结果作综合分析，不难看出：对于大跨度PC连续梁桥的主跨跨中下缘压应力σz和主跨跨中挠度fl/2，预应力损失将导致σz减小和fl/2增大，其中，σz减小主要由顶、底板钢束预应力损失所致，fl/2增大主要由底板钢束预应力损失所致，三重组合、双重组合损失类型相对于单一损失类型时的σz和fl/2结果表现为叠加关系；桥梁一阶自振频率n不受纵向预应力损失影响，因此，对于在役大跨PC连续梁桥，很难通过n的变化来识别其纵向预应力的损失状况。

4 结论

对于大跨度PC连续梁桥纵向预应力的顶、底、腹板钢束的预应力损失类型(单一、双重组合和三重组合损失类型)与损失程度对桥梁主跨跨中下缘压应力σz、主跨跨中挠度fl/2和桥梁一阶自振频率n的影响，在本文研究背景下，可以得出如下结论：

a.无论发生何种损失类型，预应力损失程度与σz和fl/2的关系均为线性相关规律。

b.预应力损失将导致σz减小和fl/2增大，其中，σz减小主要由顶、底板钢束预应力损失所致，fl/2增大主要由底板钢束预应力损失所致，三重和双重组合损失类型相对于单一损失类型时的σz和fl/2结果表现为叠加关系。

c.桥梁一阶自振频率n不受纵向预应力损失影响，因此，对于在役大跨度PC连续梁桥，很难通过n的变化来识别其纵向预应力的损失状况。