基于神经网络和改进遗传算法的混凝土水化热管冷参数优化
葛庆雷,郭德胜,陈明芳,张祖军
(1.浙江交工集团 西南分公司,贵州 贵阳 550000;2.湖南联智科技股份有限公司,湖南 长沙 410000;3.长沙理工大学 土木工程学院,湖南 长沙 410000)
0 引言
随着桥梁建设规模的不断增大,上部结构跨径越来越大,下部结构承台体积也随之变大。大体积混凝土在浇筑时,由于水泥水化热现象的存在,混凝土内部温度会在短期内急剧上升,而混凝土材料本身抗拉强度较低,温度冷却后由巨大温差产生的拉应力极易使混凝土出现开裂的情况,因此采取管冷措施对大体积混凝土浇筑时产生的水化热进行降温是十分必要的措施。杨慧[1]等基于Midas Civil软件对大体积混凝土承台水化热温度场进行了仿真模拟,采取多种施工措施达到了对承台混凝土的温度控制;占玉林[2]等通过分析大体积混凝土水化热温度场的分布规律,得到了布置冷却水管后的水化热温度降低效应;宋福春[3]等对考虑管冷的大体积混凝土水化热展开有限元数值计算,并得到了针对工程实际的最优管冷参数;胡健中[4]等结合实测数据分析了混凝土水化热温度峰值的关键影响因素,给出了相关的施工建议。
以上研究多基于实测数据或有限元计算对混凝土水化热的控制展开分析,本文以某大跨双塔斜拉桥为工程背景,首先基于BP神经网络建立了混凝土水化热的温度预测模型,并通过实测数据和有限元分析验证了模型的有效性,其次建立了混凝土水化热管冷参数的数学优化模型,使用改进的遗传算法求得设计变量的最优解,并代入神经网络预测模型验证管冷参数优化后的最终降温效果,可为今后类似的工程提供一定的参考。
1 基于BP神经网络的混凝土水化热温度预测模型
1.1 混凝土水化热温度场计算原理
1.1.1混凝土水化热放热模型
混凝土水化热,即混凝土在水化过程中水泥与水发生水化反应所产生的热效应,要确定大体积混凝土水化热的温度场分布情况,首先要定义混凝土的水化放热模型,常用的混凝土水化放热模型有指数型、双曲线型和复合双指数型,最常使用的指数型水化热放热经验模型如式(1)所示:
Q(t)=Q0(1-e-mt)
(1)
式中:Q(t)为单位质量混凝土在第t天的累积水化热;Q0为单位质量混凝土在无时间限制下的最大累积水化热;m为水化热系数,与水泥的材料特性有关;t为混凝土龄期。
绝热温升是假定混凝土边界处于隔绝热量的状态下,水化热的累计温度上升,混凝土的最终绝热温升计算如式(2)所示:
(2)
式中:T0为混凝土的最终绝热温升;Wc为水泥用量;Q为水泥的水化热性能;C为混凝土的比热容;ρ为混凝土的容重。
混凝土水化热的温度场分布机制复杂,受边界条件和材料特性的影响,其内部温度分布随机性大且不稳定,但在热传导理论基础上,结合初始条件与边界条件,可以确定唯一的混凝土温度场模型。
1.1.2考虑管冷作用的热传导方程
对各向均匀、同性的混凝土固体取一无限小的微分六面体,根据热量平衡原理,混凝土温度升高吸收的热量等于内部水化作用产生的热量与外部环境流入的净热量之和,根据冷凝管对混凝土内部温度的降低作用,将冷凝管按负热源进行处理,故简化后的固体热传导方程如式(3)、式(4)所示:
(3)
(4)
式中:a为导热系数;T1为混凝土外表绝热下条件下考虑管冷和绝热温升的最终温升;T0为混凝土的浇筑温度;Tw为冷却水的初始温度;Ψ为考虑管冷作用下混凝土水化热的变化系数;Φ为假定无热源情况下,由冷却水与混凝土温度差形成冷却系数。
混凝土温度有4种不同的边界条件,本文所研究的桥梁承台大体积混凝土属于混凝土水化热温度场分析的第3类边界,即混凝土与空气接触。假定混凝土表面热流量和表面温度与环境温度之差成正比,则定义的边界条件如式(5)所示:
(5)
式中:β为混凝土表面放热系数;Ta为环境介质的温度;λ为导热系数;n为表面外法线方向。
1.2 基于BP神经网络的混凝土水化热温度场预测模型
1.2.1BP神经网络的基本原理
神经网络模型是一种基于生理学的智能仿生模型,具备自我学习、自我训练和自动适应的能力,BP神经网络是基于反向传播算法的多层前馈型神经网络,其基本原理是通过学习、存储和修正大量的输入变量与输出变量间的关系,建立一种无须预先定义的映射关系,本文采用标准的3层BP神经网络实现对混凝土水化热的温度预测,神经网络结构如图1所示。

图1 BP 神经网络基本结构Figure 1 Basic structure of BP neural network
由图1可知,3层BP神经网络模型由输入层、隐含层和输出层组成,训练过程包括正向传播和反向传播。模型的学习原理为输入变量经过隐含层建立一定的映射关系传向输出层,当输出层数值与样本数据之间的误差超过限制时,算法进入反向传播的修正过程,重新建立神经元之间的连接关系,更新连接权值与阈值。
1.2.2基于BP神经网络的混凝土水化热预测模型设计
为提高BP神经网络模型的训练效率,对影响温度的部分因素进行简化与合并,输入参数与输出参数如表1所示:

表1 BP 神经网络设计参数Table 1 BP neural network design parameters结构层参数符号备注X1Q1单位体积混凝土温升X2a导热系数输入层X3T0混凝土浇筑温度X4Ta环境温度X5Φ冷却系数输出层{Y1,Y2…,Yt}{T1,T2…,Tt}水化热时间序列值
1.2.3BP神经网络模型训练
本文工程背景为某大跨双塔斜拉桥,主跨296 m,边跨75 m,全桥为双索面半漂浮体系。该桥主墩承台平面采用八边形结构,混凝土等级为C40,承台混凝土浇筑期间环境温度平均值为15℃,冷却管直径32 mm,进水温度为10 ℃,冷却水流量为2 m3/h,选取第1批浇筑混凝土核心温度为研究对象,承台基本尺寸、管冷布置方式如图2所示。

图2 承台与冷水管尺寸(单位:cm)Figure 2 Cap and cold water pipe size(Unit:cm)
根据规范规定的温度监控方案,当混凝土表面温度与环境温度之间的差值小于20 ℃时,停止测温,将20组温度实测值作为训练样本输入Matlab中的神经网络工具箱进行训练拟合,本文隐含层节点为11个,停止训练条件为双控,即控制预测精度和控制训练次数,达到训练条件后停止训练并记忆网络权值,本文对混凝土水化热BP神经网络温度预测模型的训练过程如图3所示。
使用基于Abaqus二次开发的子程序建立该承台大体积混凝土的水化热温度场模型[5],用于验证神经网络模型预测结果的可靠性,承台的整体浇注有限元模型如图4所示。

图3 BP神经网络训练过程Figure 3 BP neural network training process

图4 承台混凝土浇筑有限元模型Figure 4 Finite element model of concrete pouring of cap
取实测值、神经网络预测值、有限元模拟值进行对比,计算结果如图5所示,根据结果可知,本文的混凝土水化热温度神经网络预测模型达到了较好的拟合效果,达到优化模型的基本需求。
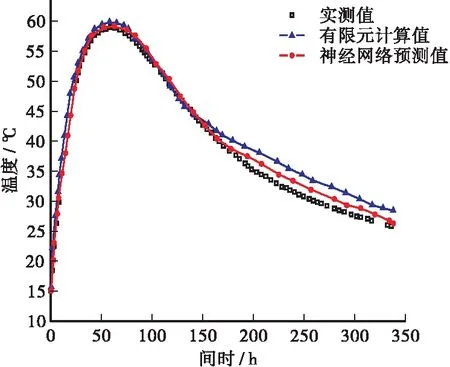
图5 混凝土水化热温度拟合结果Figure 5 Fitting results of concrete hydration heat temperature
2 改进遗传算法的管冷系统优化模型
2.1 管冷参数优化模型
仅考虑管冷对混凝土水化热的影响时,大体积混凝土水化热冷却的因素主要有冷却水进水温度、冷却水流量、冷水管直径、冷水管分布形式等,根据优化求解的研究思路,本文将混凝土水化热的平均温度作为优化模型的目标函数,选取冷却水进水温度、冷却水流量和冷水管管径作为优化参数,建立优化求解模型如式(6)所示:
(6)

由于冷却水进水温度、冷却水流量,以及冷水管管径取值必须在合理范围内,故该优化模型的约束条件为该3个优化参数的取值范围,且最优解为目标函数取最小前提下,优化参数降温效率最高点。
2.2 改进遗传算法的应用
2.2.1自适应遗传算法
遗传算法是一种基于生物进化论、遵循自然选择和遗传学理论的模拟自然进化的计算模型,它对目标函数没有连续性限定,直接通过对结构对象操作完成全局寻优。传统的遗传算法面对复杂的非线性优化问题容易出现寻优能力不足、使得算法陷入局部最优解等情况。为实现对混凝土水化热管冷参数的最佳优化效果,本文采取一种改进后的自适应遗传算法[6],通过调整变异率和交叉率达到对子代精英个体的保留,具体的改进方法如下。
a.调整变异率Pm和交叉率Pc如式(7)、式(8)所示:
(7)
(8)
式中:Pm为变异率;Pc为交叉率;k1、k2、k3、k4为种群变异率和交叉率的自适应调整系数;fmax为种群最大适应度;f′为交叉两个体间适应度较大值;fa为种群平均适应度。
b.引入精英保留策略,如式(9)、式(10)所示:
(9)
(10)
式中:Pm1、Pc1分别为变异率和交叉率的给定概率。
通过以上改进后的遗传算法可以在保证全局搜索能力的前提下避免陷入局部极值,保证后期算法性能不下降。本文以考虑管冷措施后混凝土平均水化热温度的最小值为目标函数,遗传算法的适应度函数如式(11)所示:
(11)
式中:c为平均水化热温度估计值。
2.2.2改进的遗传算法的寻优流程
根据管冷参数的数学优化模型,基于改进遗传算法的混凝土水化热管冷参数寻优流程如下:
a.初始化种群:本文设计变量为Tw,Vw,Dw,故基因个数取为3,最大遗传代数为100,交叉概率Pc取0.7,变异概率Pm取0.5,对设计变量进行二进制编码并随机产生初始种群。
b.计算适应度函数:根据式(11)计算种群中的个体适应度。
c.抽样交叉:根据个体适应度值选出下一代个体以交叉概率Pc进行交叉并产生新个体。
d.随机变异:以变异概率Pm进行变异操作并产生新个体。
e.判断迭代条件:根据最大迭代次数判断是否输出最优解,若不满足则继续迭代。
2.3 结合BP神经网络和改进遗传算法的管冷参数优化模型
结合实测数据训练的BP神经网络预测模型和改进的遗传算法,建立混凝土水化热的管冷参数优化模型,优化模型的求解流程如图6所示。

图6 BP神经网络-改进遗传算法优化模型Figure 6 BP neural network-improved genetic algorithm optimization model
根据求解流程,管冷参数优化模型的求解模型分为2部分,首先是以改进遗传算法为基础的参数优化模型,其次在遗传算法优化流程中嵌套BP神经网络算法为基础混凝土水化热温度预测模型,实现对混凝土水化热管冷参数优化后的温度预测。
3 优化结果分析
分别选取改进遗传算法求解的最优水温、最优管径和最优流量3个优化变量代入混凝土水化热神经网络预测模型进行计算,基于神经网络和改进遗传算法优化模型的计算结果如表2所示,温度预测曲线如图7所示。
由图7可知,分别对3种优化参数调优的情况下,承台混凝土核心区水化热峰值温度对比原管冷方案下降幅度约4 ℃,各优化参数变动都能明显降

表2 设计变量优化结果Table 2 Design variable optimization results符号设计变量优化结果Tw冷却水进水温度8 ℃Vw冷却水流量2.5 m3/hDw冷水管管径42 mm

图7 混凝土核心区水化热温度预测曲线Figure 7 Prediction curve of hydration heat temperature of concrete core area
低承台混凝土核心区水化热的温度,但不同参数对混凝土水化热的降温作用存在一定的差别,增大冷却水流量对混凝土水化热的降温作用最为明显,而增大冷水管管径对混凝土水化热的降温作用有限。
降低冷却水进水温度至8 ℃的情况下,混凝土核心区峰值温度降低3.5 ℃,累计水化热降低约21.6%。由于混凝土与冷却管的温差较大,降低进水温度可以加大冷却管与混凝土间的热交换效率,增强降温效果。
增大冷水管管径至42 mm的情况下,混凝土核心区峰值温度降低3.7 ℃,累计水化热降低约13.2%。增大冷水管管径可以增大混凝土与冷水管之间的接触面积,但在水流量一定的前提下,管内冷却水流量会降低,使得低温冷却水无法快速到达冷水管内部,降低对核心区混凝土水化热的降温效率。
增大冷却水流量至2.5 m3/h情况下,混凝土核心区峰值温度降低4.6 ℃,累计水化热降低约36.4%。在一定程度上增大冷却水流量可以使整个冷却管保持较低的温度,将混凝土与冷却管之间的热交换效率维持在较高的水平,实现最佳降温效果。
4 结论
本文对某双塔斜拉桥承台大体积混凝土浇筑时产生的水化热进行研究,通过建立BP神经网络温度预测模型和改进遗传算法的管冷参数优化模型,达到对混凝土水化热的最佳降温效果,通过分析可以得到如下结论:
a.BP神经网络方法不需要传统的经验模型进行拟合,避免了因参数取值不准而造成的预测数据失真问题,本文基于某双塔斜拉桥承台混凝土浇筑时的水化热实测数据建立的神经网络预测模型具有较好的拟合效果,拟合精度高于有限元模拟结果。
b.相较于传统遗传算法,基于改进遗传算法对混凝土水化热管冷参数建立的寻优模型可以有效避开局部极值,迅速收敛至各参数的最优解,达到对目标函数的优化。
c.在维持其他条件不变的情况下,改进遗传算法优化模型寻得的最优冷却水流量可以实现对混凝土水化热的最佳降温效果,神经网络温度预测模型显示混凝土最高核心温度降低4.6 ℃,累计水化热降低约36.4%,降温效果明显。

