随机海浪的滤波器模型及仿真

乔倩， 范菊

(上海交通大学 海洋工程国家重点实验室， 上海 200240)

安全性在船舶设计工作中至关重要。由大幅度横摇引起的船舶倾覆问题，往往会造成不可估量的损失。目前船舶稳性还不能完全考虑随机海浪对船舶大幅横摇以及倾覆的影响。因此，随机波浪下的船舶横摇倾覆问题的研究对指导船舶稳性规范修订方面具有重要意义[1]。

船舶及海洋结构物在随机波浪上的运动相应于一个动力系统在随机干扰下的响应，当研究随机波浪下船舶大幅非线性横摇运动所导致的倾覆问题时，不可避免地需要用到概率统计的方法进行求解。在时域内研究概率特性最有效的工具是马尔可夫过程理论[2]，当外干扰为白噪声或过滤白噪声时，动态系统的响应是一个马尔可夫过程，其转移概率密度满足一个统称为Fokker-Planck方程的线性微分方程[3]。对于马尔可夫过程理论应用于船舶及海洋结构物在随机波浪上的响应方面，Naess等[4]采用路径积分法通过解Fokker-Planck方程研究了随机海浪中结构物慢漂运动的响应。朱新颖等[5]对船舶在白噪声波浪上的倾覆问题的研究中，利用路径积分法和有限差分法2种方法在时间域内求解相应的Fokker-Planck方程，给出船舶横摇运动响应随时间演变的概率密度分布。柴威[2]在时域内求解Fokker-Planck方程的基础上，进一步探讨了外部激励、横摇阻尼以及非线性复原力矩对船舶横摇运动响应转移概率密度的影响。沈栋等[6]采用路径积分法通过解Fokker-Planck方程研究了随机横浪下船舶横摇倾覆问题。何诚亮等[7]对船舶在真实海况下的倾覆问题的研究中，利用路径积分法和有限差分法在时间域内求解相应的Fokker-Planck方程，给出接近真实海况下的船舶大幅横摇运动响应概率密度分布情况。

在应用马尔可夫理论到船舶在随机波浪下的运动问题时，由于实际海浪具有有限的谱宽和给定的谱密度函数，属于有色噪声激励[8]，因此需要将白噪声外干扰项通过滤波器转换为有色噪声激励。通过引入合适的滤波器模型，可以使该问题的解决更接近实际情况。

Spanos[9]将ARMA滤波算法引入到波浪模拟中，对实际的海浪谱进行拟合。为了更好地将ARMA过程应用到运动微分方程，Brockwell等[10]提出了时间连续的CARMA过程。随后，滤波方法被广泛应用于船舶与海洋工程领域的波浪载荷模拟和非线性系统的响应评估中。沈栋等[6]采用由二阶时间连续的AR模型构造的滤波器对白噪声进行滤波处理，得到滤波后的船舶横摇的随机微分方程。何诚亮等[7]利用二阶CARMA模型制作滤波器，将输入的白噪声转化为有色噪声以模拟真实海况的海浪谱，改善了二阶AR滤波器对海浪谱的拟合程度。Chai等[11]采用高阶CARMA模型的滤波器，将白噪声外载荷转换成有色噪声载荷。

本文利用CARMA过程，给出构造不同阶数的滤波器的统一方法，系统的探讨了不同阶数的滤波器模型可行性。对各滤波器参数进行最小二乘拟合，使滤波器生成谱逼近海浪谱，为模拟随机海浪的有色噪声激励奠定基础。通过将不同滤波器生成的波浪时历进行统计值比较，从而为海浪模拟提供有效的滤波器形式。

1 随机海浪的时间序列

像随机海浪波面升高的时间序列可用自回归滑动平均过程ARMA建模。ARMA过程的谱密度由多项式的商组成，能够很好地逼近给定的海浪谱[9]。此外，因为船舶运动通常是用微分方程来模拟的，所以还需要引入时间连续的CARMA过程[10]。

ARMA的基本思想是将预测对象看作一串随时间变化且又相互关联的随机序列[12]，并采用相应的数学模型进行描述分析，从而在最小方差的层面达到最佳预测。ARMA模型具有3种表现形式：自回归模型(auto-regressive，AR)，滑动平均模型(moving-average，MA)以及自回归滑动平均模型(auto-regressive moving-average，ARMA)。

自回归滑动平均模型一般为时间离散的差分方程，考虑到在时间连续的情况下，这一差分方程可以改写为微分方程的形式[13]。引入时间连续的自回归滑动平均模型即CARMA模型(continuous-time ARMA)，该模型对应的线性微分方程表达式为：

x(p)(t)+a1x(p-1)(t)+a2x(p-2)(t)+…+apx(t)=

ε(t)+b1ε(1)(t)+b2ε(2)(t)+…+bqε(q)(t)

(1)

式中上标代表对t的导数的阶数。

考虑一个CARMA(p,q)过程y(t),用状态空间的形式来表达：

y=c′u(t)

(2)

式中状态向量u(t)∈Rp，并满足线性Ito微分方程：

du(t)=Au(t)dt+bdW(t)

(3)

式中：W是维纳过程；dW(t)=W(t+dt)-W(t)是单位维纳过程的一个增量；dW(t)/dt为白噪声序列，取其功率谱密度S(ω)≡1。

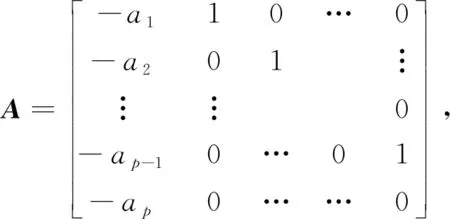
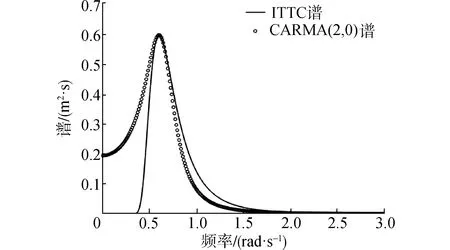
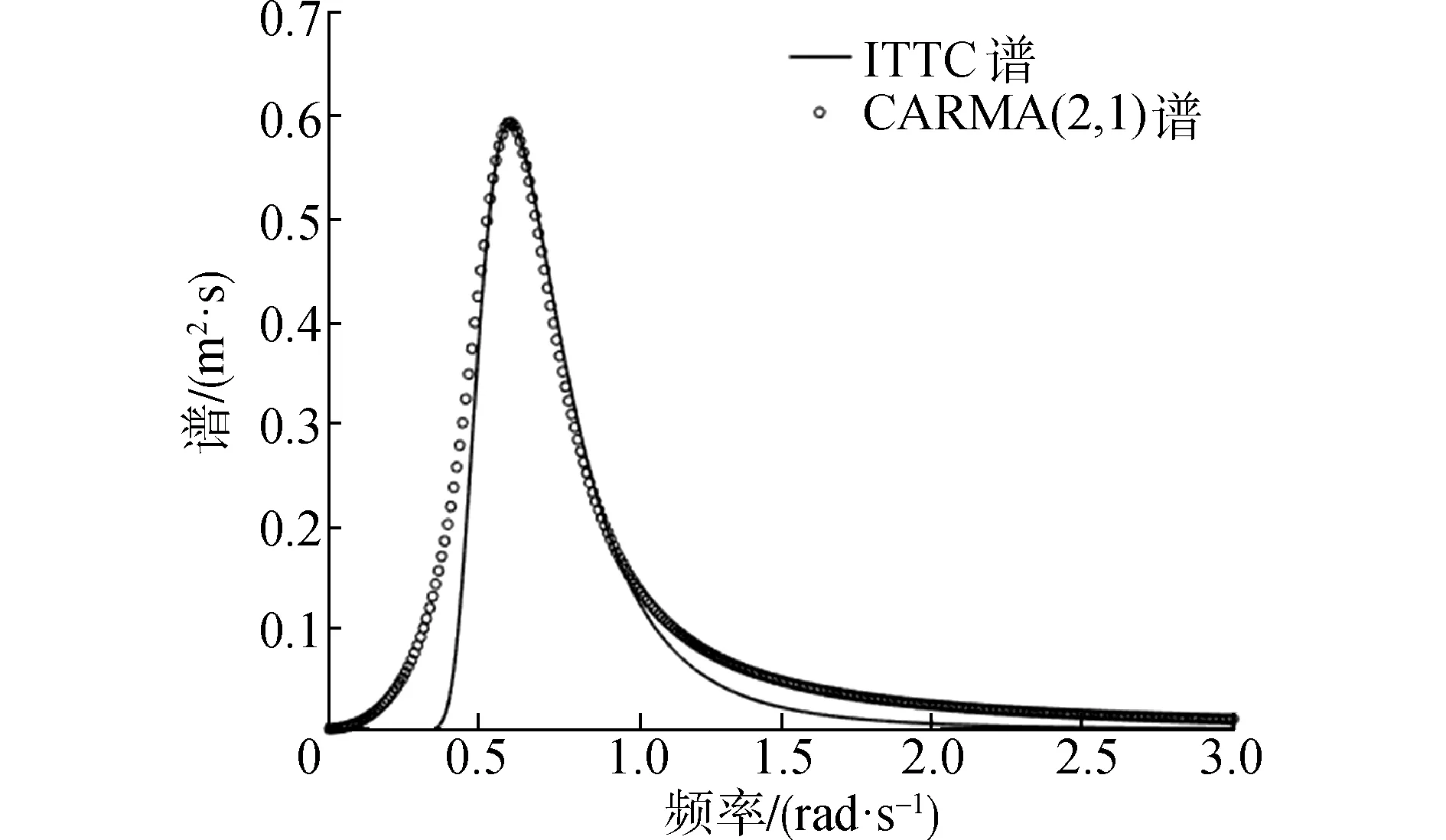
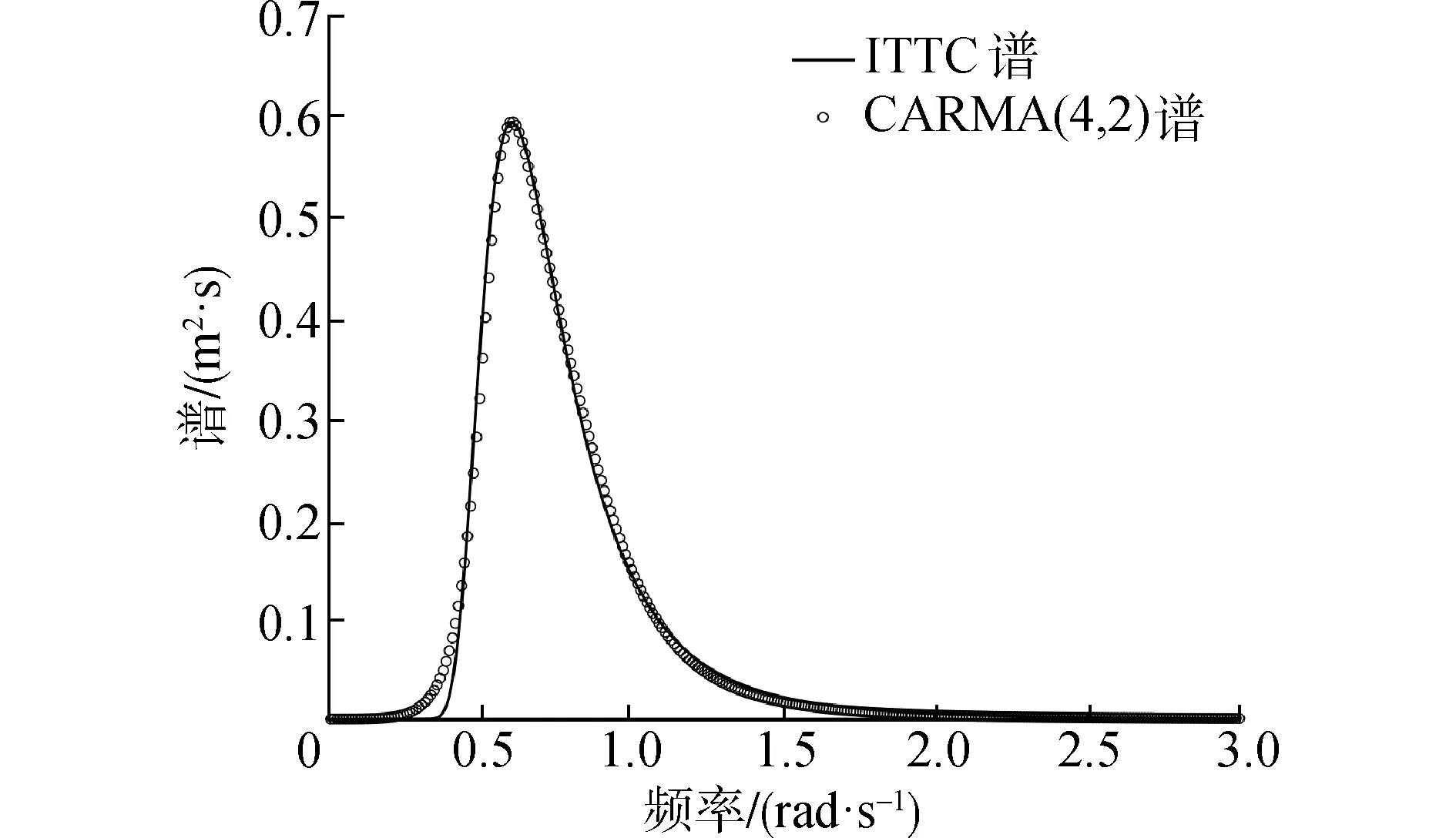
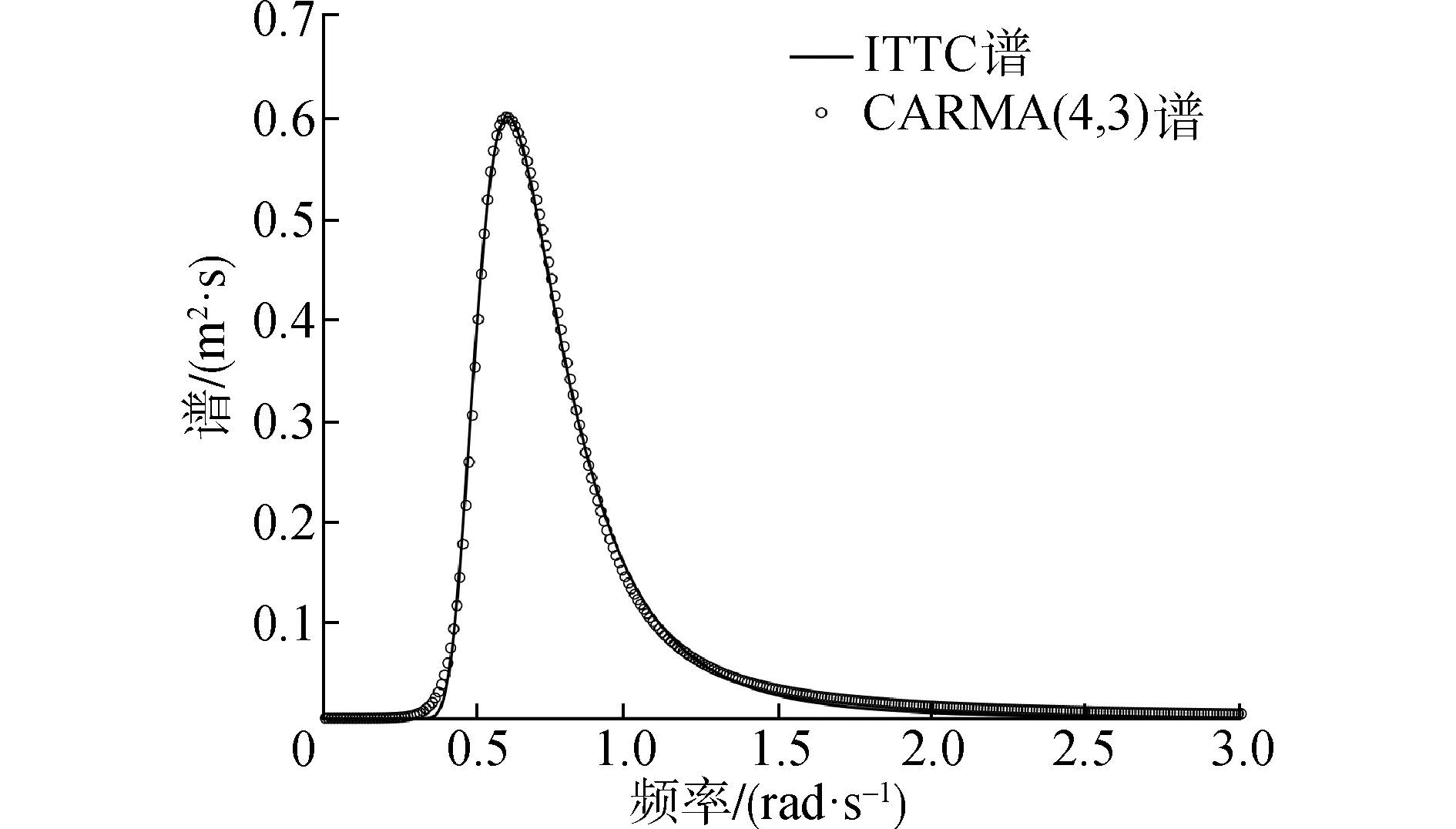
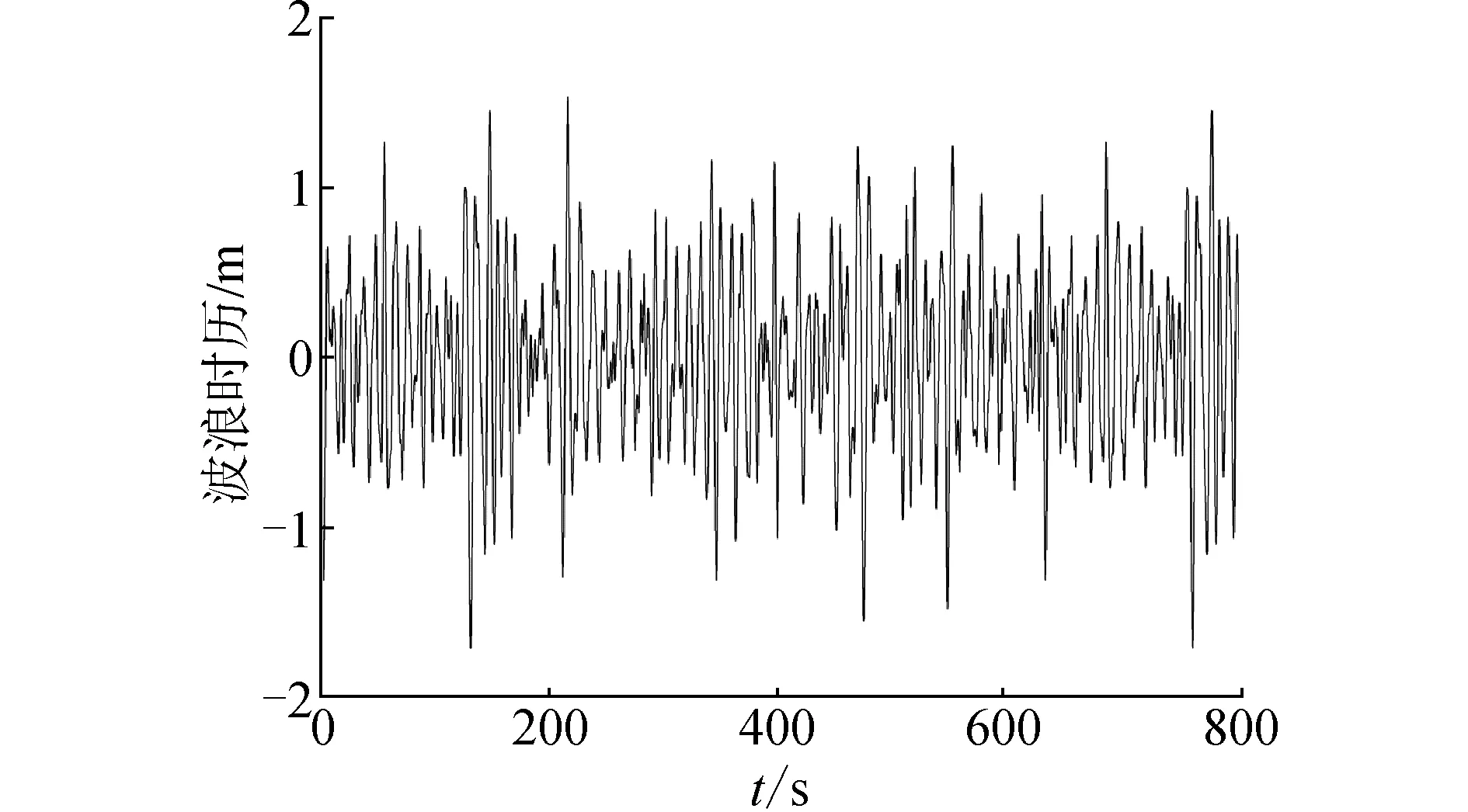
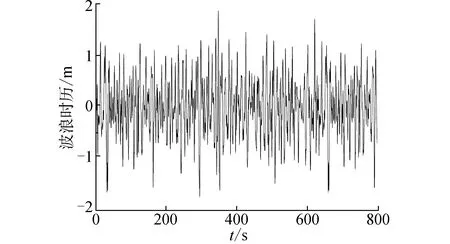
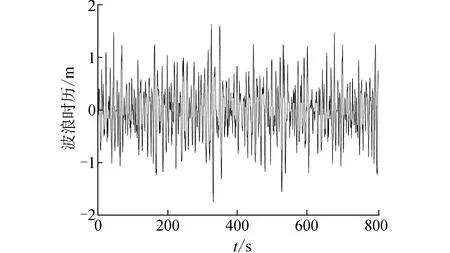
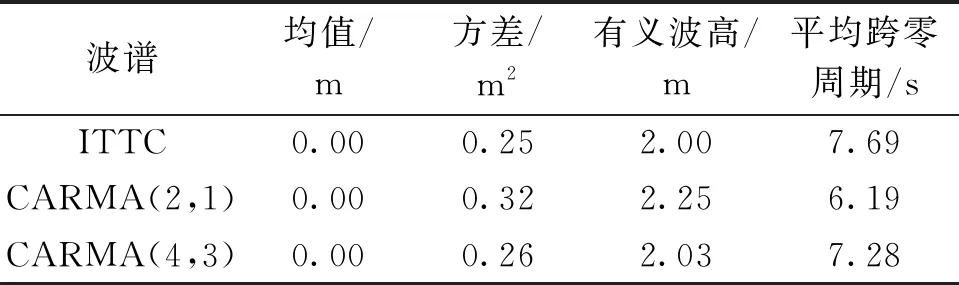
式中0≤q

上述CARMA(p,q)过程对应的谱密度为：

(4)

式中s=iω。值得注意的是该定义所给出的CARMA模型的状态空间表示方法并不是唯一的。

2 滤波器模型

工程上一般将影响船舶运动的波浪当作平稳随机过程来处理。输入白噪声作为外载荷干扰，并引入合适的滤波器对其进行滤波处理，获得符合一定统计特性的有色噪声，以模拟真实海况的海浪谱。

2.1 ITTC双参数谱

本文采用ITTC双参数谱[14]作为标准海浪谱。它是第15届国际船模拖曳水池会议所推荐的，以有义波高和特征周期为参数，结构简单，适用于充分成长的海浪。其表达式为：

(5)

式中：H1/3是有义波高；T1是特征周期。

图1是四级海况对应的ITTC双参数谱，其中有义波高H1/3=2 m，特征周期T1=8 s。由图1可以看出，实际的海浪具有一定的谱密度函数并且谱宽有限，表现为有色噪声而非白噪声，因此在随机问题的求解中需要引入滤波器模型对白噪声输入做滤波处理。

图1 ITTC双参数谱曲线形状

本文以ITTC双参数谱为标准海浪谱，构造滤波器模型对海浪谱进行逼近，给出了由几种不同阶数的CARMA(p,q)过程构造的滤波器模型。

2.2 二阶滤波器

2.2.1 CARMA(2,0)模型

通常情况下，一阶自回归AR(1)模型在随机运动及载荷领域的应用非常广泛，而船舶及海洋结构物所涉及的运动响应至少是二阶的。因此，首先采用时间连续的CARMA(2,0)模型来构造滤波器。为了将问题简化处理，此二阶模型只考虑了自回归部分，没有考虑滑动平均部分，对应的微分方程为：

(6)

式中：输出用y表示，代表波面升高；输入为谱密度恒等于1的白噪声序列，用dW(t)/dt表示；ai是自回归参数，bj是滑动平均参数。该CARMA(2,0)模型滤波器的传递函数为：

(7)

对应的谱密度为：

(8)

为了近似拟合本研究所采用的四级海况对应的ITTC双参数谱，采用最小二乘法来确定各参数值。该滤波器的参数取值为a1=-0.4，a2=0.447 4，b0=0.196 4。将该滤波器所对应的功率谱曲线与ITTC双参数谱进行对比，如图2所示。

图2 CARMA(2,0)滤波器生成谱与ITTC谱对比

该滤波器生成谱可以大致体现随机海浪的统计特性，然而在低频部分与实际情况相差较大，因此需要采取一定方法对上述缺陷加以改善。

2.2.2 CARMA(2,1)模型

AR模型适合处理全极点谱，MA模型适于处理全零点谱。而现有的用于描述随机海浪的波谱同时包含极点和零点，需要用极零点模型表达。因此在前述的二阶滤波器基础之上，增加对滑动平均部分的考虑，采用CARMA(2,1)模型构造滤波器，对应微分方程的表达式为：

(9)

该CARMA(2,1)模型滤波器的传递函数为：

(10)

对应的频谱公式为：

(11)

采用最小二乘法对本研究所采用的ITTC双参数谱曲线近似拟合，该CARMA(2,1)滤波器模型的参数取值为a1=-0.37，a2=0.367 4，b1=0.284 6。

图3为该滤波器对应的有色噪声功率谱与ITTC双参数谱。同时对比图2和图3可以发现，相较于第1种只考虑自回归模型的CARMA(2,0)滤波器，第2种同时考虑自回归与滑动平均的CARMA(2,1)滤波器模型对应的有色噪声功率谱更接近ITTC双参数谱，能够更好地反映随机海浪的统计特性。

图3 CARMA(2,1)滤波器生成谱与ITTC谱对比

从图3可以看出，虽然滑动平均部分的加入改善了自回归模型的不足，但是CARMA(2,1)模型对实际海浪谱的拟合仍存在缺陷，在低频段及高频段都略高于ITTC双参数谱。为了更加精确地模拟描述真实海浪统计特性的海浪谱，需要考虑构造更高阶数的滤波器模型。

由于三阶滤波器模型对ITTC双参数谱拟合程度的改善效果不太明显，下面给出四阶滤波器模型。

2.3 四阶滤波器

为了使滤波后的有色噪声更加符合真实海浪的统计特性，需要用到更高阶的滤波器模型。四阶滤波器依然是基于自回归滑动平均模型构造得到，这里探讨不同四阶滤波器模型的拟合效果。

2.3.1 CARMA(4,1)模型

由四阶自回归模型和一阶滑动平均模型构成的CARMA(4,1)滤波器表达式为：

(12)

对应的频率响应函数为：

(13)

对应的功率谱密度函数为：

(14)

该CARMA(4,1)四阶滤波器的各参数取值为a1=-0.312，a2=1.275，a3=0.073 8，a4=0.372，b1=0.153。滤波器生成谱见图4。

图4 CARMA(4,1)滤波器生成谱与ITTC谱对比

从图4可以看出，四阶滤波器的生成谱对ITTC双参数谱的拟合度明显优于二阶滤波器。但是在细节方面，低频区域略高于ITTC双参数谱，高频区域略低于ITTC谱。而根据前述二阶滤波器的模拟情况，高阶的MA模型恰恰可以解决这个问题。高阶的MA模型可以降低低频区域的谱密度值，并且提高高频区域的谱密度值。下文将采用高阶MA模型的四阶CARMA滤波器。

2.3.2 CARMA(4,2)模型

CARMA(4,2)滤波器由四阶自回归模型和二阶滑动平均模型构成，表达式如下：

(15)

传递函数的表达式为：

(16)

对应的功率谱密度函数为：

(17)

该四阶滤波器的各参数取值为a1=-0.932，a2=1.265，a3=-0.41，a4=0.243，b2=0.201。滤波器生成谱见图5。

图5 CARMA(4,2)滤波器生成谱与ITTC谱对比

从图5可以看出，由四阶AR模型和二阶MA模型组合而成的CARMA(4,2)滤波器对应的有色噪声功率谱，除了在低频区域仅有一小部分略高于ITTC双参数谱，在大部分区域近乎完全拟合。由此可见，四阶滤波器模型已能够很好地实现对实际海浪谱的模拟。不过，为了改善滤波器对应的功率谱密度在低频区域略高于实际海浪谱的这个缺陷，考虑引入三阶的MA模型做进一步探讨。

2.3.3 CARMA(4,3)模型

由四阶自回归模型和三阶滑动平均模型构成的CARMA(4,3)滤波器表达式为：

(18)

对应的传递函数的表达式为：

(19)

对应的功率谱密度函数为：

(20)

CARMA(4,3)滤波器模型的各参数取值为a1=-0.677 5，a2=0.9，a3=-0.237，a4=0.143，b3=0.183 5。滤波器生成谱见图6。

图6 CARMA(4,3)滤波器生成谱与ITTC谱对比

对比图6与图5，MA模型阶数的增加使得CARMA(4,3)滤波器生成谱明显改善了在低频区域对描述实际海浪统计特性的ITTC双参数谱的模拟效果。在高频区域，该滤波器生成谱不能完全趋近于零，但基本接近零。整体来看，CARMA(4,3)数学模型滤波器的生成谱与ITTC双参数谱高度契合，可以用来实现对真实海浪统计特性的描述。

从上面的分析可以看出，四阶滤波器CARMA(4,3)对ITTC双参数谱的拟合效果最好。但是滤波器阶数的提高会大大增加实际问题求解过程中的计算成本[15]。例如在利用有限差分法数值求解船舶横摇运动响应转移概率密度分布随时间的变化时，在每一个递进的时间步长内，若只考虑用白噪声作为船舶横摇运动微分方程的外干扰输入项，则对应的二维FPK方程的求解区域按50×50均匀网格离散化，网格数为502；若引入二阶滤波器模型对白噪声进行滤波处理，则对应的四维FPK方程的求解区域按50×50×50×50均匀网格离散化，网格数为504；若将四阶滤波器与船舶横摇运动微分方程联立，对白噪声进行滤波，则相应的六维FPK方程求求解区域按50×50×50×50×50×50均匀网格离散化，网格数为506。区域网格数以几何级数增长，会大大增加计算耗时。

因此在选择滤波器数学模型时，应综合考虑拟合精度与计算复杂度。低阶滤波器建议选择CARMA(2,1)模型，高阶滤波器建议选择CARMA(4,3)模型，下面将主要针对这2个滤波器进行海浪的模拟及验证。

3 随机海浪的仿真与验证

滤波器生成谱与ITTC双参数谱的拟合程度从理论上给出了利用CARMA模型构造滤波器来对随机海浪进行模拟的可行性。利用滤波器对波浪时历进行数字模拟，并根据时历得出的统计值与原波谱统计值进行对比，可以进一步探讨不同阶滤波器生成的随机海浪与原随机海浪的统计特性差异程度。

3.1 随机海浪的数学模型

实际海面上的波浪主要由风产生，是一种非常复杂的随机过程。由于风向的多变性和风的随机性，风浪可能向各个方向传播，起伏的波面就像形状不等的小丘。在本文中，为使问题简化，假定海浪只沿一个固定方向传播，其波峰线和波谷线彼此平行且垂直于波浪的前进方向，这种海浪被称作“二元不规则波”，或长峰波海浪。

在随机海浪研究中，以Longuet-Higgins模型[16]在工程中的应用最为广泛。Longuet-Higgins模型认为长峰波海浪可以看作由无数个不同波幅、频率与初相位的余弦波叠加而成。固定点海浪波面位移可表示为：

(21)

式中ζAi、ωi、εi分别为第i个余弦波的波幅、频率和初相位。其中εi为0～2π均匀分布的随机相位。

振幅ζAi与谱之间的关系：

(22)

3.2 海浪的仿真与验证

已知有义波高H1/3=2 m，特征周期T1=8 s的四级海况对应的ITTC双参数谱，以及前文所推荐的CARMA(2,1)和CARMA(4,3)滤波器对应的有色噪声功率谱，根据Longuet-Higgins模型生成波浪时历，对海浪波面的瞬时值进行模拟。

由ITTC谱和CARMA(2,1)、CARMA(4,3)2种滤波器生成谱对应的波浪时历如图7～9所示。

图7 基于ITTC谱生成的波浪时历

图8 基于CARMA(2,1)谱生成的波浪时历

图9 基于CARMA(4,3)谱生成的波浪时历

表1为CARMA(2,1)和CARMA(4,3)2种滤波器所生成波浪时历的统计值与ITTC谱生成的波浪时历对应的统计值的对比。

表1 波浪时历统计值的比较

由表1可以看出，基于自回归滑动平均模型构造的CARMA(2,1)二阶滤波器所生成的波浪时历统计值，比较接近ITTC双参数谱对应的统计值。而由CARMA(4,3)四阶滤波器生成的波浪时历统计值更接近ITTC双参数谱对应的统计值，对应的方差、有义波高、平均跨零周期的相对误差分别是4%、1.5%、5.3%。

根据上面对功率谱和生成的波浪时历统计值的比较结果，可以得出在精度要求不高的情况下，可采用CARMA(2,1)二阶滤波器得到随机波浪。而对于CARMA(4,3)滤波器来说，无论是从波谱曲线的形状趋势，还是所生成波浪时历的统计值，该四阶滤波器的功率谱都与ITTC双参数谱有着更高的契合度。滤波器阶数的提高虽然使其表达式更为复杂，但却保证了对实际海浪更高精度的模拟效果。值得注意的是，在进行随机海浪的数字仿真时，要同时考虑计算复杂度与模拟精度这两方面的要求来选择滤波器模型。

4 结论

1)二阶滤波器结果表明，MA模型的引入可以极大地改善单纯用AR模型对海浪谱的拟合程度。具有极零点谱形式的ARMA过程适用于海浪谱的模拟。

2)基于ARMA过程，可以构造多种形式的滤波器模型。四阶滤波器生成谱与ITTC双参数谱的契合程度优于二阶滤波器，但是在实际问题的求解中应综合考虑对模拟精度与计算复杂度的要求。

3)结合滤波器生成谱，利用Longuet-Higgins模型进行波浪时历仿真，生成的时历数据统计值与ITTC双参数谱对应的时历统计值之间的相似程度进一步验证了由ARMA过程构造的滤波器模型模拟随机海浪的可行性。