盾构引起的管线变形特性及近接影响分区研究
孔 杰,荣传新*,施 鑫,王厚良,孙学军
(1.安徽理工大学土木建筑学院,安徽 淮南 232001;2.安徽建工集团股份有限公司建筑设计研究院,安徽 蚌埠 233000)
随着城市地铁建设的普及,部分线路在规划时不可避免地会下穿地下市政管线。而盾构隧道近距离下穿管线时,开挖扰动及管-土相互作用极易引起路面沉降和管线受力变形甚至破坏,对城市地下管网及地表建筑物构成极大威胁。
目前众多学者针对盾构下穿既有管线进行了相关研究。文献[1]利用参数优化后的Pasternak模型研究了土体弹性模量、管隧夹角等因素对管道竖向位移及弯矩值的影响。文献[2]采用连续弹性介质模型和Pasternak模型分别建立了隧道下穿管线时管线挠度和弯矩的解析解。文献[3-4]利用能量法求解出盾构施工时管线的沉降,并对计算结果进行了对比验证。文献[5-6]通过数值模拟软件建立管线-土体-隧道三维数值模型研究了开挖过程中隧道尺寸及管线埋深等因素对管线位移的影响。文献[7-8]通过实验和数值模拟分析了管线在隧道盾构施工时的位移及内力特征。文献[9]研究了隧道近距下穿管线的爆破振动特征及安全标准。文献[10]研究了地下工程中近接施工时的力学原理与对策。文献[11]进行了地铁施工中临近管线的安全风险管理的研究。文献[12]研究了双线盾构隧道施工时邻近地下管线的安全性判别方法。
综上所述,目前研究大多集中于既定隧道盾构施工对既有地下管线的影响性分析,而针对隧道-管线相对位置近接程度判别标准及隧道近接下穿既有管线强弱影响分区的划分还不全面。因此,科学地预测评估掘进过程对既有管线的影响对于实际工程具有重要意义。本文以合肥地铁4号线桐-潜区间盾构隧道近距离下穿混凝土雨水管线工程为背景,通过现场实测及数值模拟,利用以单因素分析为基础的多元非线性逐步回归方法,分别进行基于地表沉降和管道变形的双线隧道近接施工影响分区的划分,以期为双线隧道近接下穿既有管线风险评估提供借鉴。
1 近接施工影响判别标准
盾构近接施工影响判别标准是划分近接施工强弱影响区的依据。根据两阶段法[13]原理,盾构隧道施工会对周围地层产生扰动,引起初始位移场;在管道周围地层位移场形成过程中,管土受管道刚度影响产生协同变形,管道最终位移量小于管道中心线地层初始位移量。因此,地层沉降量和管道变形量是判别盾构下穿管道影响程度的重要因素。一般情况下,盾构法施工时,应控制地表沉降值不超过30mm,地表隆起值不超过10mm[14],故采用-30~+10mm作为地表变形的控制标准。当地表沉降U≥10mm或者U≤-30mm时,属于强影响区;当5mm≤U<10mm或-30mm 根据GB50141-2008《给排水构筑物工程施工及验收规范》和GB50268-2008《给排水管道工程施工及验收规范》中的相关规定以及现场对刚性管线变形控制的相关标准,取5mm作为混凝土雨水管的变形控制阀值。当管线沉降U≥5mm或U≤-10mm时,属于强影响区;当2.5mm≤U<5mm或-10mm 合肥地铁4号线桐城路站至潜口路站区间为双洞单线隧道,全长534.8m,左、右线均为小半径曲线型隧道,隧道埋深14m,外径6m,两隧道中心线距离为15m。区间双线隧道垂直下穿一条深埋混凝土雨水管,管道埋深8m,外径1.8m,壁厚0.18m。本区间范围内共有6个地层,自上而下依次为杂填土、⑥2黏土、⑦1黏土、风化砂质泥岩、强风化砂质泥岩、中风化砂质泥岩,隧道和管线均位于⑥2黏土层中,管隧位置及相关测点如图1所示,土体基本物理力学参数指标如表1所示。 图1 管隧位置及管线测点分布图 表1 岩土体基本物理力学参数 为消除边界效应的影响,模型尺寸取为100m×60m×50m。兼顾计算时间与计算精度,盾构开挖区域网格尺寸取为1m,而模型边界采用较粗的网格尺寸约为3m。由于管道结构对于模型计算结果影响较大,故作加密处理,取单元尺寸为0.4m。整体模型包括81 635个节点和125 065个单元。结合桐潜区间盾构掘进参数实时监测结果,模型中模拟盾构时开挖面掘进压力取P1=120kN/m2、盾构千斤顶力取P2=570kN/m、注浆压力取P3=300kN/m2。 模型中仅考虑管线及隧道深度范围的杂填土及黏土地层,且假定土体为理想弹塑性材料,服从修正摩尔-库伦屈服准则。地层及注浆区域采用实体单元模拟,盾构外壳、衬砌管片及雨水管采用二维板单元模拟,除地层外其余材料视为各向同性的线弹性材料。 图2(a)为左右线依次施工完成后管线正上方地表的沉降曲线及现场实测对比结果。由图2(a)可知,地表沉降模拟结果与实测结果基本吻合, 实测地表沉降槽宽度略大于模拟结果。 由模拟结果可以得出, 在左线隧道开挖过程中,地表最大沉降值出现在左线隧道上方, 约为25.9mm, 实测最大沉降22.8mm; 随着右线隧道开挖, 最大沉降值点逐渐偏移至两隧道中心线位置, 模拟结果最大沉降约为28.8mm, 实测值为26.9mm, 偏差率为6.6%。 (a)地表沉降结果对比 图2(b)显示了双线隧道贯通后管线沉降对比结果。 由图2(b)可知, 受管线刚度影响, 在管土相互作用下管线沉降小于地表沉降, 模拟得到的管线沉降规律与实测结果一致, 最大沉降偏差仅为2.1mm,偏差率为9.1%。 由图2可知,模型计算的沉降结果和变形规律与实测值基本相符,但是由于工程现场同一层位土体分布并不均匀,而在模型中同一层位的土体默认是均质各向同性的,因此实测结果与模拟结果存在一定的误差,但该模型能较好地反映隧道盾构引起的地表和管线沉降分布规律。 1.校园环境方面。好的环境对于学生的学习与成长有着积极作用。为使学生更好地接受传统文化,主动诵读经典诗文,学校方面应加强校园文化建设。譬如在文化墙上手绘《弟子规》或者是《三字经》篇章,使其成为学生的行为准则:孝敬父母、尊师重道、团结友爱、积极进取。教学楼走廊墙壁上应挂诗词名作,学校的广播站应定期定时播放经典古诗文;在班级文化建设方面也应注重经典诵读,班级中学习园地应不定时展示出学生关于经典诗文的绘画、写作及摘录作品等。通过校园文化的建设,使整个校园充满诗意,促进学生对古诗文的学习。 为分析隧道近接盾构施工引起的既有管线变形及地层沉降规律,考虑管-隧竖向净距H和隧道水平净距S两种因素的影响,其中H的取值为0.5D、1D、2D、3D,S的取值为0.5D、1D、2D、3D(D表示隧道外径,取值6m)建立16种模拟工况。模型中采用的土体计算参数与表1保持一致,施工阶段设置与前文模型相同。 本文分析了S=0.5D时4种不同管-隧净距和H=0.5D时四种不同隧道净距下的地表和管线沉降曲线的变化,如图3所示。各工况下地表的最大沉降值和管线的最大沉降值如表2所示。 (a)S/D=0.5时不同工况下地表及管线沉降变化曲线 (b)H/D=0.5时不同工况下地表及管线沉降变化曲线图3 不同工况下地表及管线沉降变化曲线 由图3(a)可知,在管线刚度影响下,各工况地表沉降均高于管线沉降。左、右线隧道净距S相同时,随着管隧净距H的增大,地表及管线最大沉降值逐渐减小,工况1地表及管线沉降分别为42mm和34mm,工况4地表及管线沉降分别为12mm和8mm,地表和管线最大沉降同比分别减少71.3%、75.9%。此外,随着管隧净距H的增大,沉降槽宽度逐渐增大,表明盾构施工对地层和管线的影响范围不断扩大。 由图3(b)可以得出,H相同时,S增大, 地层沉降的范围随之增大, 地表各点对应位置的沉降逐渐减小,S/D=3比S/D=0.5时地表及管线的最大沉降分别减少了38.2%、 41.6%。对比各工况下双线隧道盾构开挖完成后沉降曲线可以得出,当S=0.5D时,地表和管线的沉降曲线服从高斯分布;当S=1D时,地表和管线的沉降曲线已经由V形逐渐过渡为U形;当S=2D时沉降曲线已不再满足高斯分布,近似呈W形。隧道净距增加至3D时,沉降曲线呈明显W形,且左线隧道上方沉降峰值略高于右线隧道,说明当两隧道间距S>3D时,后施工隧道对先施工隧道的影响可以忽略不计,可单独考虑两线隧道开挖对地层和管线产生的影响。 表2 各工况下地表/管线最大沉降值 mm 根据文献[15]的研究可知,管线在隧道盾构面推进过程中产生的沉降可以通过Gauss公式进行拟合,如下所示 (1) i=K(zt-zp) (2) 式中:Smax为管线沉降最大值,m;x为隧道中心线到管线的距离,m;i为沉降槽宽度,m;K为管线埋深处的沉降槽宽度系数;zt为区间隧道埋深,m;zp为管线埋深,m。 (3) 然后进一步分析盾构施工引起的管线内力变化规律。选取S=0.5D时4种不同管隧竖向净距和H=0.5D时4种不同隧道水平净距下的管线弯矩进行分析,弯矩分布曲线如图4所示。 (a)不同H下管线弯矩分布曲线 (b)不同S下管线弯矩分布曲线图4 不同工况下管线弯矩分布曲线 由图4(a)可知,在隧道净距一定时,管线的最大正、负弯矩值均随着管隧净距的增大而减小,H/D=3相比H/D=0.5时管线弯矩值减少了95.5%。4种工况下的管线最大正弯矩值都出现在管线中点位置,说明管线中心底部承受最大拉应力;随着管隧净距H的增大,管线最大负弯矩值逐渐偏离管道中心位置,表明管道顶部最大拉应力位置逐渐远离管线中心。 从图4(b)中可以看出,4种工况下管线最大正、负弯矩值出现的位置均随着隧道净距的增大而增大。S=0.5D时,由于管线沉降曲线整体呈V形,因此该工况下管线的弯矩分布曲线仅有1个正弯矩峰值;当S=1D时,弯矩分布曲线开始出现两个正弯矩峰值,且管线中线正弯矩值逐渐减小;随着S的进一步增大,正弯矩双峰值间距离逐渐增加且峰值基本相同,管线负弯矩由双峰值变为3峰值,表明隧道净距的增大不仅会改变管线拉应力极值出现的位置,还会增加管线拉应力极值的个数。 根据前文不同工况下数值模拟计算结果,本次近接施工影响分区的划分主要考虑管-隧道竖向净距H和隧道水平净距S两个因素的影响,依据文献[16]提出的基于单因素分析结果的多元非线性逐步回归方法,得到了基于地表沉降和管道变形的双线隧道近接施工强弱影响分区。 首先,对不同管隧净距下的地表最大沉降与自变量S/D进行回归分析,设其函数表达式为 U=y+AeB(S/D) (4) 通过拟合得到4个不同H/D下的回归公式,如图5所示。 图5 不同H/D下地表最大沉降U与S/D的回归关系 然后, 将变量H/D与函数表达式中的3个参数y、A和B再次进行回归, 得到y=-8.17709-47.03253e-2.14104(H/D), 拟合优度R2=0.988,A=-6.40864-94.004e-2.69182(H/D), 拟合优度R2=0.993,B=-0.68536-2.28333e-3.37403(H/D), 拟合优度R2=0.916。 最后,得到U与S/D及H/D的回归表达式为 U=[-8.17709-47.03253e-2.14404(H/D)]- [6.40864+94.004e-2.69182(H/D)]· e[-0.68536-28333e-3.37403(H/D)](S/D) (5) 根据式(5)可以将S/D表示成H/D和沉降量U之间的函数关系,如式(6)所示 (6) 以H/D为横坐标,S/D为纵坐标, 将地表沉降强弱影响分区的控制阀值-30mm和-10mm分别带入式(6)中,得到基于地表沉降的强弱影响分区曲线。按照相同的方法可以获得以管线变形值-10mm、-5mm作为判别标准的强弱影响分区曲线,双线隧道盾构施工近接影响分区曲线如图6所示。 图6 关于S/D和H/D的近接影响分区图 由图6可知,基于地表沉降的强弱影响分区均在基于管线沉降的强弱分区范围内,说明以管线沉降作为控制标准更加严格。考虑到冗余安全度的原则,选择基于管线沉降划分的影响分区相比地表沉降具有更高的安全系数。 (1)根据两阶段法原理,提出基于地表沉降阀值10mm、30mm和基于管线沉降阀值10mm、5mm的强弱影响分区控制的双判别标准。 (2)隧道净距S及管隧净距H的增大,均会引起地表及管线最大沉降值减小,沉降槽宽度增大。管线最大弯矩值随着H的增大而减小,管线正弯矩由单峰值过渡为双峰值,管线负弯矩由双峰值变为3峰值。 (3)在双线隧道盾构下穿管线近接施工的条件下,当管线与隧道垂直时,选择基于管线沉降划分的影响分区比基于地表沉降划分的具有更高的安全系数。 (4)上述结论是针对合肥地区黏土地层并基于管隧垂直这一特殊工况下获得的,而对于其他地区不同地质条件下管隧平行或斜交时的近接施工强弱影响分区还需进一步研究。2 近接施工模拟分析及验证
2.1 工程概况
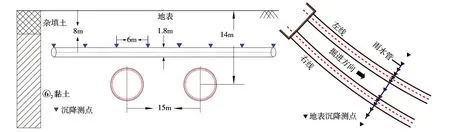

2.2 模型的建立
3 结果分析及验证

3 盾构下穿既有管线计算结果分析
3.1 地表和管线沉降分析

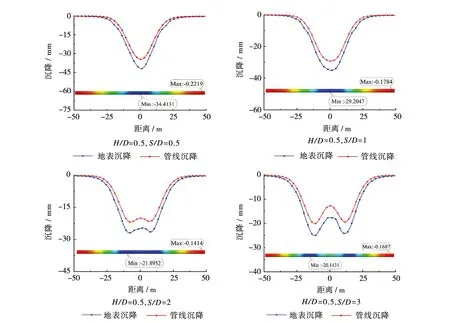

3.2 管线弯矩分析

3.3 近接施工影响分区划分



4 结论与展望

