环形剪切开孔软钢阻尼器参数优化设计
杨明飞,王 娟,王 磊,陈宜网
(1.安徽理工大学土木建筑学院,安徽 淮南 232001;2.安徽圣沃建设工程有限公司综合管理部,安徽 合肥 230031)
金属阻尼器具有造价低廉、滞回性能稳定、耗能能力良好等优点[1],其耗能性能主要受阻尼器形状和几何参数的影响[2]。目前,针对阻尼器形状和几何参数对其耗能性能的影响研究较多。文献[3]通过实验考察了两种不同截面构成的金属剪切型阻尼器的力学性能。文献[4]研究了新型混合摩擦金属被动阻尼器的垫片所受摩擦力的大小对其耗能能力和有效等效黏滞阻尼比的影响。文献[5]研究了C 形阻尼器的垂直和水平直径、厚度和深度和其屈服力、耗能性能的相关性。文献[6]研究了环形Q235钢板阻尼器的圆弧半径和钢板厚度、宽度对其耗能性能的影响。文献[7]分析了新型波形软钢阻尼器不同波角、厚度及腹板和翼缘材料的强度比对阻尼器各性能参数的影响。文献[8]101分析了钢板厚度、开孔数量及开孔尺寸等参数对环形剪切开孔软钢阻尼器力学性能的影响。文献[9]建立了一种基于Kriging代理模型和遗传算法进行结构形状优化的工程方法,文献[10]基于此方法提出开孔形状优化方法。文献[11]对菱形开孔剪切型金属阻尼器的开孔形状进行了优化。
现有研究大都是对金属阻尼器的形状和几何参数性能影响研究和阻尼器形状优化设计,鲜有对阻尼器几何参数进行优化设计。本文基于Kriging代理模型,针对文献[8]102所提出的环形剪切开孔软钢阻尼器进行参数优化设计,以期提高该阻尼器的耗能性能。
1 阻尼器数值分析
环形剪切开孔软钢阻尼器耗能钢板平面如图1所示。为了分析钢板厚度、开孔数量及开孔尺寸等参数对阻尼器耗能性能的影响,文中设计了6组试件,具体参数尺寸如表1所示。
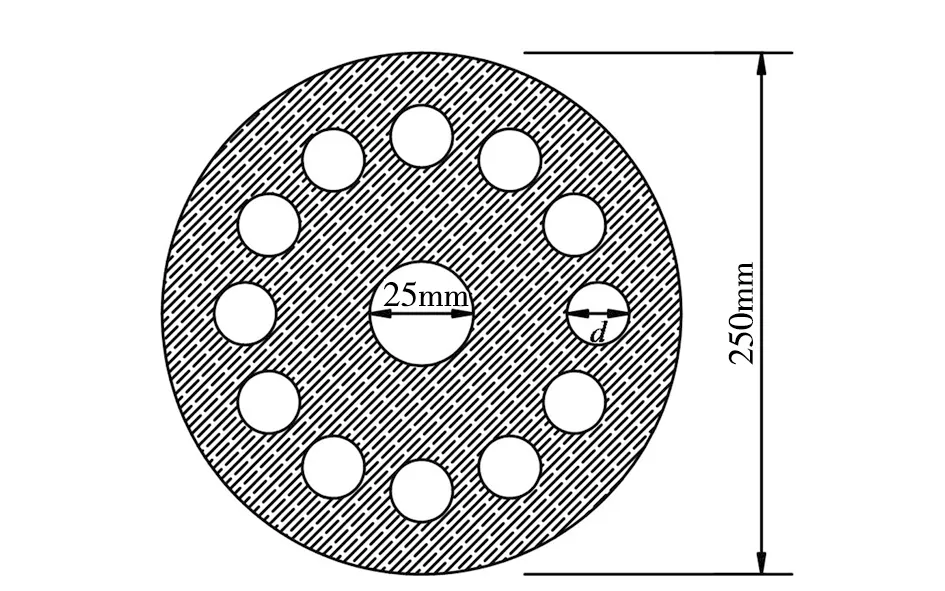
图1 阻尼器耗能钢板平面示意图

表1 阻尼器的具体参数尺寸
为了得出阻尼器自身的相关性能指标,文中采用有限元软件ANSYS模拟阻尼器的循环加载试验,加载方式采用控制位移加载法-低周循环往复加载,其位移幅值分别为2.5mm、5mm、10mm、15mm、20mm。提取阻尼器在不同位移幅值下的滞回曲线,从而计算得出其滞回面积、等效应变能和等效黏滞阻尼系数,具体结果如表2所示。

表2 阻尼器的耗能性能指标
由表1和表2可知,钢板厚度对阻尼器的耗能性能影响较大,增加钢板的厚度有利于提高阻尼器的耗能性能;而开孔率对阻尼器的耗能性能影响一般,当开孔率由0.12增大至0.18时,阻尼器耗能性能降低不明显;当开孔率由0.18增大至0.24时,阻尼器耗能性能降低较大。这说明可以通过优化阻尼器的几何参数提高其耗能性能。
2 基于Kriging代理模型优化方法
1.1 拉丁超立方抽样
在建立代理模型之前,首先需要进行抽样设计,所建立的代理模型精度通常取决于抽取样本点的数量和样本点在空间分布的均匀性。拉丁超立方抽样[12-13]是一种近似随机抽样的多维分层抽样方法,其特点是每一个样本点在小空间内随机地分布,且所有样本点投影到任意一维时,每一个小区间内有且仅有一个样本点。本文采用MATLAB软件里的lhsdesign函数来进行拉丁超立方抽样。
2.2 Kriging模型
在对自变量进行抽样设计后,需要通过数值模拟的方法得到与样本点相对应的响应值,从而建立设计变量与响应值之间关系的代理模型。Kriging模型是一种半参数化的插值方法,包含多项式和随机过程两部分[14],其数学模型可描述为
(1)
式中:f(βi,X)为多项式,本文选取1阶多项式模型;βi为回归系数列向量;zi(X)为随机过程,其具有如下的统计特性
E[zi(X)]= 0
Var[zi(X)]=σi2
Cov[zi(xk,xj)]=σi2R(θ,xk,xj)
式中:R(θ,xk,xj)为两个样本点之间的相关函数,表征任意两个样本点xk、xj之间的相关性。
本文采用MATLAB软件自带的一种Kriging工具箱DACE建立Kriging模型,DACE工具箱主要包含根据样本点构建Kriging模型的dacefit函数和根据Kriging模型计算待测点的响应值的predictor函数。
在Kriging模型建立后,还需要另取样本点来检验模型的精度,以保证模型的有效性。利用模型预估响应值与实际响应值的相关性r2检验Kriging模型的精度,当r2≥0.95时可认为模型精度满足要求,计算公式为
(2)
2.3 遗传算法
遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法[15]。在建立Kriging代理模型后,需要在设计变量取值范围内寻找出使得响应值最大的样本点,但所建立Kriging代理模型通常较为复杂,可能出现多个峰值点,利用一般的优化方法可能会被限制在局部最优点而不是全局最优。为了解决这个问题,本文采用遗传算法进行优化。应用遗传算法时首先对设计变量的染色体进行编码,然后随机生成一定规模的初始种群,初始种群数量取为50,再通过适应度函数的计算评价种群中个体的优劣程度,适应度函数公式如下
F=136.3e0.053t-25200k4.219-74
(3)
式中:F为恢复力,kN;k为耗能钢板的开孔率;t为取整后的耗能钢板厚度,mm。
接着利用选择、交叉和变异等操作得到新一代种群,交叉概率、变异概率、迭代次数等参数均为默认值,随后再对新的种群进行适应度计算,循环选择、交叉和变异操作,如此迭代下去,直到计算收敛,得到全局最优解,优化过程结束。具体可通过使用MATLAB软件中的遗传算法工具箱GA Toolbox实现。
3 算例
3.1 问题描述
本文对环形剪切开孔软钢阻尼器的几何参数进行优化,其目的在于提高阻尼器的耗能性能。在优化问题中,以钢板厚度t和开孔率k为两个设计变量,并以阻尼器的耗能性能E为优化目标,阻尼器的耗能性能可通过滞回曲线的滞回面积表示。
已有研究结果表明,阻尼器构造参数与其性能基本呈正相关,即增大钢板厚度或减小开孔率,阻尼器耗能能力随之提高,从而阻尼器自身用料增加、制作成本增加和刚度增大[8]105。在实际工程应用中,提高阻尼器的耗能能力固然重要,但制作成本的增加和阻尼器刚度的增大会影响结构的自身振动特性,不利于结构抗震,并且也不符合经济性的要求。因此,在一定的制作成本的情况下(即阻尼器总用料一定),优化阻尼器的耗能性能作为本文优化问题的一个约束条件。
因此,本文的优化设计以尽可能少的阻尼器制作成本来达到甚至提高预期的耗能性能为目标,即安全性与经济型的双重优化。以ASPD-1试件的参数尺寸(钢板厚度为18mm、开孔率为0.18)为阻尼器的原始尺寸,则阻尼器的总用料为
W=(1-k)tS=14.76S
(4)
式中:W为阻尼器耗能钢板的总用料,mm3;k为阻尼器耗能钢板的开孔率;t为阻尼器钢板厚度,mm;S为无孔耗能钢板的横截面积,mm2,为定值。
将k=0.18,t=18代入公式W=(1-k)tS中,经计算可得W=(1-k)tS=14.76S,则约束条件可以表示为
(5)
同时, 基于阻尼器的原始尺寸, 经过大量的数值分析和模型参数调整, 最终确定两个设计变量的取值范围为: 钢板厚度t的取值上下限分别为20mm和10mm,开孔率k的取值上下限分别为0.24和0.06[8]105。
综合上述条件,本次优化设计问题可用数学模型表示为
findx=[t,k]
minf(x)=-E
subjected to (1-k)t≤14.76S
also 10≤t≤20, 0.06≤k≤0.24
3.2 优化过程及结果分析
确定好设计变量的取值范围、优化目标及约束条件后,要利用拉丁超立方抽样方法进行样本点的抽取。一个优化问题需要进行训练点和检测点两次抽样,若设计变量维度为n,则抽取的训练点数为10n,测试点数为5n(n<5)和2n(n≥5)[16]。本文优化问题共两个设计变量,则需要抽取20个训练点来拟合Kriging代理模型和10个检测点来验证代理模型的精度。在样本点抽取后,利用ANSYS有限元软件进行数值模拟得到与样本点相对应的响应值。表3给出了20个训练点的具体数据与其对应的响应值。为了贴切实际和便于计算,本文将抽取样本点后的钢板厚度参数进行了取整。

表3 样本点具体数据及其响应值
基于以上20个训练点及其对应的响应值,利用MATLAB-DACE工具箱建立Kriging代理模型并检验其精度。图2给出了所建立的Kriging代理模型的响应面。
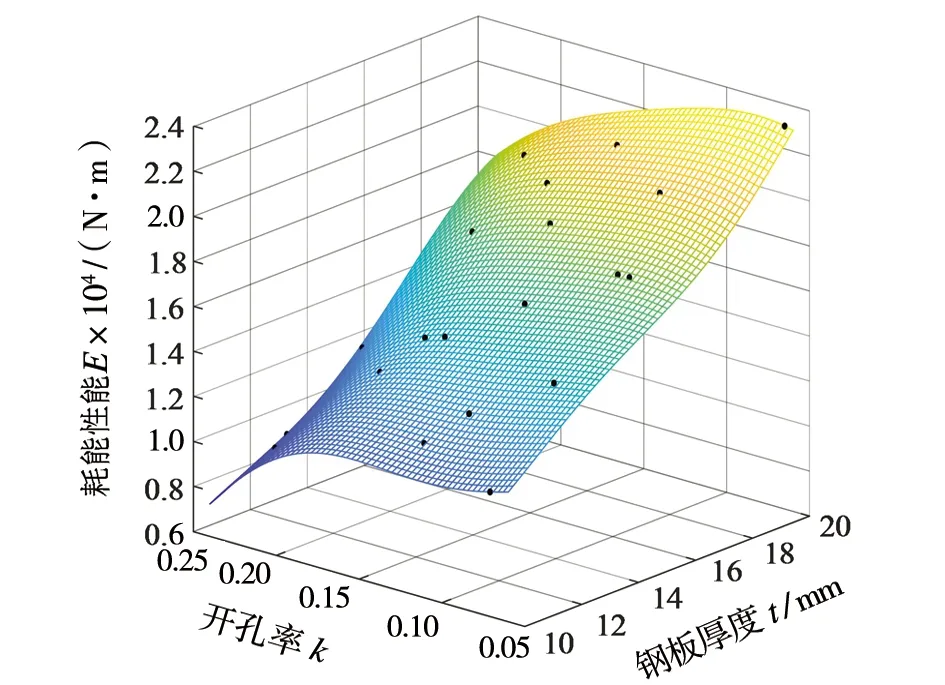
图2 Kriging代理模型响应面
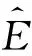

表4 Kriging代理模型的精度检验结果
由表4可知,代理模型预测的响应值与数值分析得到的响应值之间的相关性均不小于0.95,可见该代理模型的精度较高,对设计变量所预测的响应值较为准确,可以进行下一步的优化工作。
应用遗传算法对设计变量在其可行域及约束条件内进行寻优,设置初始种群规模为50,交叉概率为0.8,变异概率为0.1,迭代次数为50,以Kriging代理模型作为适应度函数,遗传算法的迭代搜索过程如图3所示。

图3 迭代搜索过程
由图3可以观察出,迭代搜索过程显示出了较好的收敛状态,适应度最大值很快地趋于一个常数,而适应度平均值随着迭代次数逐渐逼近适应度最大值,向着全局最优解发展,并经过约30次迭代后收敛,得到最大适应度值为20 119.43N·m,即遗传算法在设计变量的可行域内搜索到优化目标阻尼器耗能性能E的最大值为20 119.43N·m。
基于Kriging代理模型的阻尼器参数优化结果:优化前的钢板厚度为18mm,开孔率为0.18,耗能性能为18 952.69N·m,总用料为14.76S;优化后的钢板厚度为17mm,开孔率为0.178,耗能性能为20 119.43N·m,总用料为13.97S。由参数优化结果可知,经遗传算法优化后,得到了最佳的阻尼器参数,其耗能性能也得到了优化,提高了6.2%,并且总用料降低了5.4%,实现了以尽可能少的制作成本达到预期效果,甚至提高了耗能性能,达到了安全性与经济型的双重要求,同时也证明了基于Kriging代理模型的优化设计方法的有效性。
4 结论
本文建立了环形剪切开孔软钢阻尼器的参数与其耗能性能之间的Kriging代理模型,提出该阻尼器的参数优化设计方法。 通过Kriging代理模型的预测响应值与有限元软件数值的响应值对比分析发现,其相关性均不小于0.95,表明此模型拟合精度较高。 遗传算法优化分析结果表明, 环形剪切开孔软钢阻尼器的耗能能力提高了6.2%, 且总用料降低了5.4%, 实现了安全性与经济性的双重优化。
本文基于钢板厚度和开孔率两个参数提出了环形剪切开孔阻尼器耗能的优化设计方法, 但忽略了钢板内径、 外径等参数的影响, 未来将以此为基础, 针对该阻尼器其他几何参数提出优化设计方法。

