P-Net框架下的小样本雷达信号识别算法

徐帅， 刘鲁涛

(哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

当代雷达技术发展鼎力突进，新的雷达信号调制技术不断涌现，更多的信号类别进入信息化战场。这使得信息样本不充分的未知LPI雷达信号识别难问题日益突出。目前雷达信号识别的方法主要有2类：匹配模板方法、特征提取组合机器学习的方法[1]。此2类方法总体上实现了对全部雷达信号的有效识别，但是作为特征分析的主要手段，无论是人工分析还是机器学习，均需要建立在较大数量的标签信号样本的数据基础之上。

譬如传统方法以人工提取的信号特征参数为依据，早期文献[2]中LPI雷达信号的识别借助最大似然估计，对时域瞬时变化的某些统计特征进行分析和建模。对于PSK、FSK等经典调制方式具有可观的识别效果，但这种识别方法依赖一定数据量下的标签信号的人工分析，方才能建立出该类型信号适用的多维特征匹配模板。

文献[3]尝试将神经网络搭建引入信号调制方式识别的领域中，实现信号的自动分类识别，为往后LPI雷达信号识别开启了新思路。进入深度学习的框架领域后，国内外学者在该方向做了诸多探索。Kong等[4]通过时频分析建立LFM、Costas、BPSK等12种LPI雷达信号时频数据集，并使用CNN对该12种信号进行分类识别，低信噪比下识别率达90%。纵观近年来这一领域方法的研究，思路是将LPI雷达信号的时频域信息通过各种卷积神经网络，去自动拟合出一个高维的分类函数。训练的过程需要和标签信号做有监督学习，也意味着需要大量的标签样本提供训练支持，以此训练出一个期望的分类函数[5]。可以视为人工智能分类对传统人工识别的一种优化尝试[6]，但是依然没能解决需要大量已知的标签样本的问题。

面对当下复杂的信息战场环境中的大量的小样本信号，信息样本严重不足，常规的特征学习框架具有明显的局限性。虽然，文献[7]提出了一种基于多视角子空间聚类的无监督雷达信号识别方法，但是其完全脱离训练样本的策略在面对较复杂的识别任务时，聚类效果不佳[8]。

本文就对信号因信息样本不足，无法通过训练拟合的问题，提出一种基于原型网络P-Net(prototypical networks, P-Net)[9]的识别算法。获取小量信号样本的时频信息，拟合出整体信号的分类函数。该算法摒弃了常规的交叉熵损失[10]，通过优化充足类样本点和类原型的相对位置使得充足类样本点在空间类间分散、类内聚合[11-12]，得到的模型具有泛化能力。在测试过程中，小样本信号通过现有小样本的微调，可实现对全部类信号的识别。

1 系统概述

本节主要介绍了以P-Net和SPWVD时频分析为依托的小样本LPI雷达信号识别体统的结构组成及各模块功能。

如图1所示为小样本雷达信号识别系统的结构组成，该系统主要由3部分组成，时频图像获取，图像预处理与P-Net神经网络训练与测试。

图1 基于P-Net的小样本雷达信号识别系统结构组成

前两部分中时频分析是为了将时域数据转化为二维的时频数据矩阵。数据矩阵经过Imresize等预处理操作，可以集中呈现时频信息的关键部分，简化一些空白的冗余信息，为后续的识别网络的训练拟合和自动分类识别做好准备[13]。第3部分识别网络是本章的重点。原型网络是用来做小样本分析训练的一种神经网络，在得到前两部分处理完的雷达信号时频信息以后，可以在有限数量的雷达信号时频信息样本条件下，发掘样本之间的联系，寻求一个模型较好的空间表征。在测试的时候每个类别仅依赖于很少的几个样例就可以确定每一类的原型，以此达到小样本训练的目的。

此雷达信号识别系统避免了对庞大的标签信号样本的依赖，支持小样本训练在一定程度上优化了雷达信号识别的资源配置。

2 时频分析与图像预处理

面对多种复杂的雷达调制信号，时域和频域的独立信息有时缺乏可辨性，而在二维的时频联合域，可以清楚地辨析出各种调制方式的瞬时频率时变特性，因此，时频分析也作为雷达信号脉内识别的重要依据[14]。这里的时频信息是一个二维数据矩阵，它以图像的形式呈现。但是并不是在对图像进行研究探讨，本文关注的重点是数据矩阵中的较大数值的分布情况，它表征了信号能量在时频域的分散，这使得时频信息的识别有别于传统的图像的识别[15]。

经过参考，本文采用平滑伪Wigner-Ville分布[12](smooth pseudo WVD，SPWVD)表征时频信息。因为此部分不是本文研究的重点，直接给出它具体的数学表达并建立时频信息的图像表达。

(1)

图2是通过SPWVD变换以及Imresize的预处理过程，获取的10种常见LPI雷达信号的时频图像。

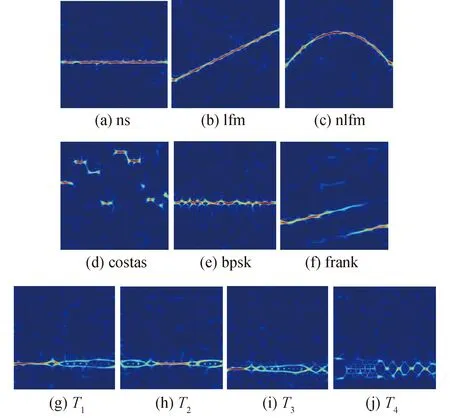
图2 LPI雷达信号的时频图像

通过上述处理，将雷达信号以时频图像的形式存储，并建立LPI雷达信号数据集。

3 识别网络

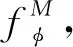
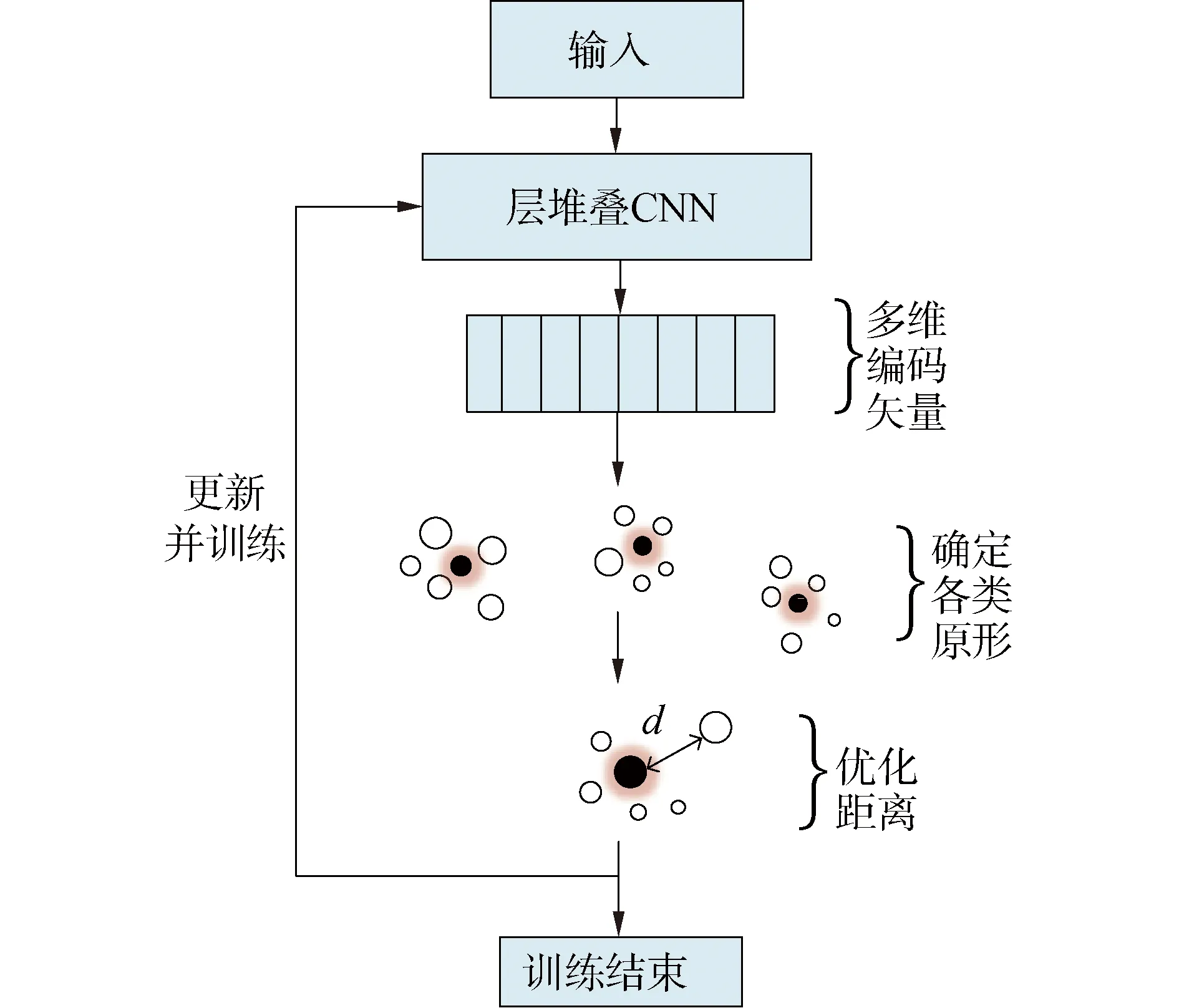
图3 P-Net结构示意

()

(2)

(3)

式中xi∈PM代表矢量点，yi∈[1,2,…,K]代表该点的标签。以图4为例，1-4是样本空间按矢量点的类分为 4个区域，图中区域面积的大小反映该类别下样本矢量点的多少。其中，1-3是样本充足类区域，4是小样本类区域。

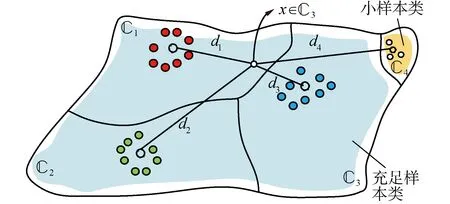
图4 P-Net的样本空间

1={(x1,1),(x2,1)…(xN1,1)}

(4)

式中N=∑Ni，N1,N2,N3≫N4。

对于每一个类别，选取该类别中所有样本点的中心c，用来表征该类别的空间信息。在运算中，选取该类样本点的坐标均值为原型(Prototypic)[5]:

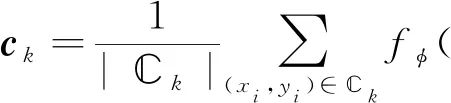
(5)

各类的原型ck∈PM承担了该类样本点在样本空间中的空间表征，而模型的训练在空间中寻求一种无序到有序的过程，如图5所示。P-Net的优化对象不同于普通卷积神经网络在概率空间取标签值的交叉熵，而是以矢量点在样本空间中到原型的欧几里得距离(euclidean distance)作为优化函数[9]:

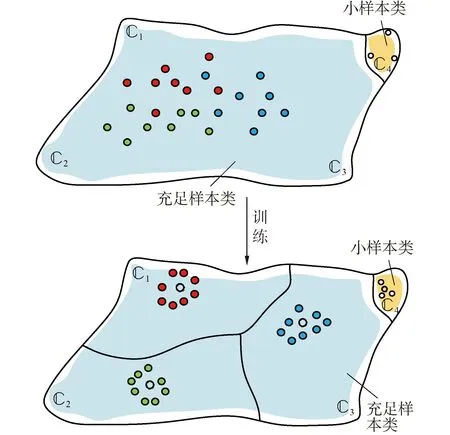
图5 P-Net训练过程

pφ(y=k|x)=softmax(dEuclido(fφ(x),ck))=

(6)

J(φ)=-logpφ(y=k|x)

(7)

其中J(φ)代表空间样本点到原型的损失函数(loss function)，对它采用SGD优化器或者亚当优化器，以BP反向传播的形式更新映射函数fφ。事实上，P-Net网络的训练过程是通过训练各类样本点在空间PM中的聚集程度，来实现映射模型fφ的获取。在某种程度上，P-Net的学习不同于一般CNN对“正确答案”——标签值的学习，而是学习样本点的空间特征表征能力，这样得到的训练模型具有一定的泛化能力。其表现在，通过充沛样本(1～3)训练得到的映射函数，对于小样本类别(4)的矢量点也具备聚集能力。

pre=k,dEuclido(fφ′(x′),ck)=Min

(8)

4 基于P-Net的LPI雷达信号识别

4.1 算法概述

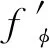
在具体的操作过程中，训练样本集以一个批次(episode)L为训练单位，其中每个批次由支持集(support-set)Ls和查询集(query-set)Lq组成(L=Ls+Lq)。

4.2 识别流程

具体识别的操作步骤如下：

1)按3中操作算法得到由雷达信号时频图构成的训练集。此训练集由足量的信号样本组成。

2)训练时，每个信号类任取Ls数量的时频信息图作为支持集，将支持集送入作为映射过程fφ的卷积神经网络，在样本空间PM得到若干支持样本点(support-points)。计算出每类支持样本点的原型。

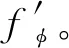
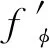
图6 P-Net训练及识别过程

5 仿真和分析

5.1 仿真参数设置

针对10种LPI雷达调制信号，通过Matlab 2016a仿真出I路和Q路的数据信息，作为初始信号信息。

10种LPI雷达调制信号数据获取的初始参数如下[12]：

NS：信号长度[500,1 024]，载频fc是U(1/4,1/8)的随机数。

LFM：信号长度[500,1 024]，带宽Δf和初始频率f0随机分布于U(1/16,1/8)。

NLFM信号：信号长度[500,1 024]，信号载频fc随机分布于U(1/20)到U(1/4)，调频斜率k随机分布于[2B/T,3B/T]。

BPSK：单序列长度为7，11，13。载波频率fc随机分布于U(1/8)～U(1/4)。循环相位码长度cpp是1～5的随机整数，码周期Np也是整数随机分布于[100,300]。

Costas码：跳频序列NF是[3～6]的随机整数，基频fmin随机分布于U(1/24,1/20)，信号长度[500,1 024]。

Frank码：载频fc随机分布于U(1/8,1/4)，循环相位码长度cpp是1～5的随机整数，步进频率M是4～8的随机整数。

T1-T4码：码序列段数k是4，5，6。编码周期T范围在[0.07,0.1]。

5.2 不同信噪比下的识别分析

本节针对小样本雷达信号的识别进行仿真实验。为了使雷达信号在复杂电磁环境中更具一般性，在上一节的10种雷达信号数据中加入高斯白噪声，选取信噪比的区间为-12～8 dB，并以步长2 dB选取若干测试点。

其中，在每个信噪比下，随机将5种信号作为充足样本类信号，剩余5种信号作为小样本类信号。P-Net的训练集由这5种充足样本类信号组成，每种充足类信号800个样本，不含小样本信号；小样本信号类的所谓的小样本为Lsmall=5带标签的时频信息图；测试集包含全部10种信号，每种信号100个样本用于测试。

在本节中，选取文献[17]的InceptionNet-v3网络、文献[18]的AlexNet网络以及文献[19]的ResNet-50神经网络作为本文P-Net分类系统的参照对象。以上三者算法与本文分类系统在信号自动识别领域有着相似性，且它们得到深度学习界广泛认可具有一定代表性。具体的，AlexNet、Inception-v3和ResNet-50属于传统的深度学习训练模式。它们都需要在足量训练样本支持的条件下，完成对信号样本的学习，属于常规而典型的有监督训练模式，这不同于本文所研究的P-Net训练模式。在仿真操作上为使信息条件等价，令每个信噪比下AlexNet、Inception-v3和ResNet-50的训练集由5类充足样本信号各800张时频图像，和5类小样本信号各5张时频图像共同组成。

使用5.1节参数去产生十种雷达信号用于本节3种系统的学习和测试。仿真对比结果如图7所示。

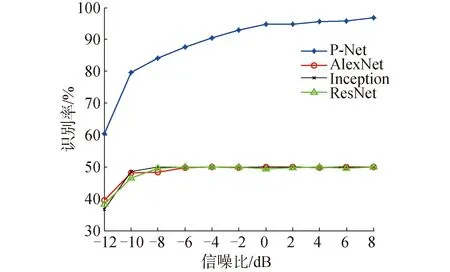
图7 整体识别正确率

P-Net系统的整体识别准确率与信噪比大小呈正相关，并且在给定等价的小样本信息条件下，P-Net的识别效果要明显优于后三者。AlexNet等常规深度学习网络架构随着信噪比的提升，识别率依然只能停滞在50%。这是因为它们能很好地学习5类足量样本信号的特征，而对另外5类小样本信号，缺乏有效的学习能力。

5.3 各参数变量对识别准确率的影响

P-Net雷达信号分类系统能根据训练样本集学习得到一个泛化的空间表征模型，然后在极少量的小样本信号条件下，完成对所有信号的分类识别。在整个过程中涉及到较多的变量条件，相关变量的改变都会影响到最后识别的正确率。

因整体识别率如图7已处于较高水准，本节主要关注信号的小样本识别率。将探讨如下3个重要变量对小样本识别率的影响：

1)充足样本类信号的训练集样本数。

充足样本类信号训练样本集的数量直接影响了模型在类中的表征精度，它与模型的刻画能力密切相关。保持其他各类参数变量不变(充足样本信号为5类，小样本信号的样本数量为5)，对该变量下不同数值大小做了统计分析，如图8所示。

图8 充足样本类信号的样本数对纯小样本识别率的影响

-8 dB以下时，系统受样本数量的影响较为明显且为正相关，信噪比较高时影响较小。但是随着样本数量的增加，纯小样本识别率的上限有所停滞无法达到100%。说明系统在上述参数条件下，识别率已达上限。

2)充足/小样本类数的相对关系。

充足/小样本类数同样和模型的表征能力密切相关。保持其他各类参数变量不变(训练信号样本数量为800，小样本信号提供的小样本数量为5)，在固定充足类数为5的条件下，观测小样本类数2～5时的纯小样本识别率；固定小样本类数为5的条件下，观测充足类数2～5时的纯小样本识别率。

对比发现，纯小样本识别率与小样本信号类数呈负相关，而受充足信号类数的影响不大。

3)小样本信号的小样本数Lsmall。

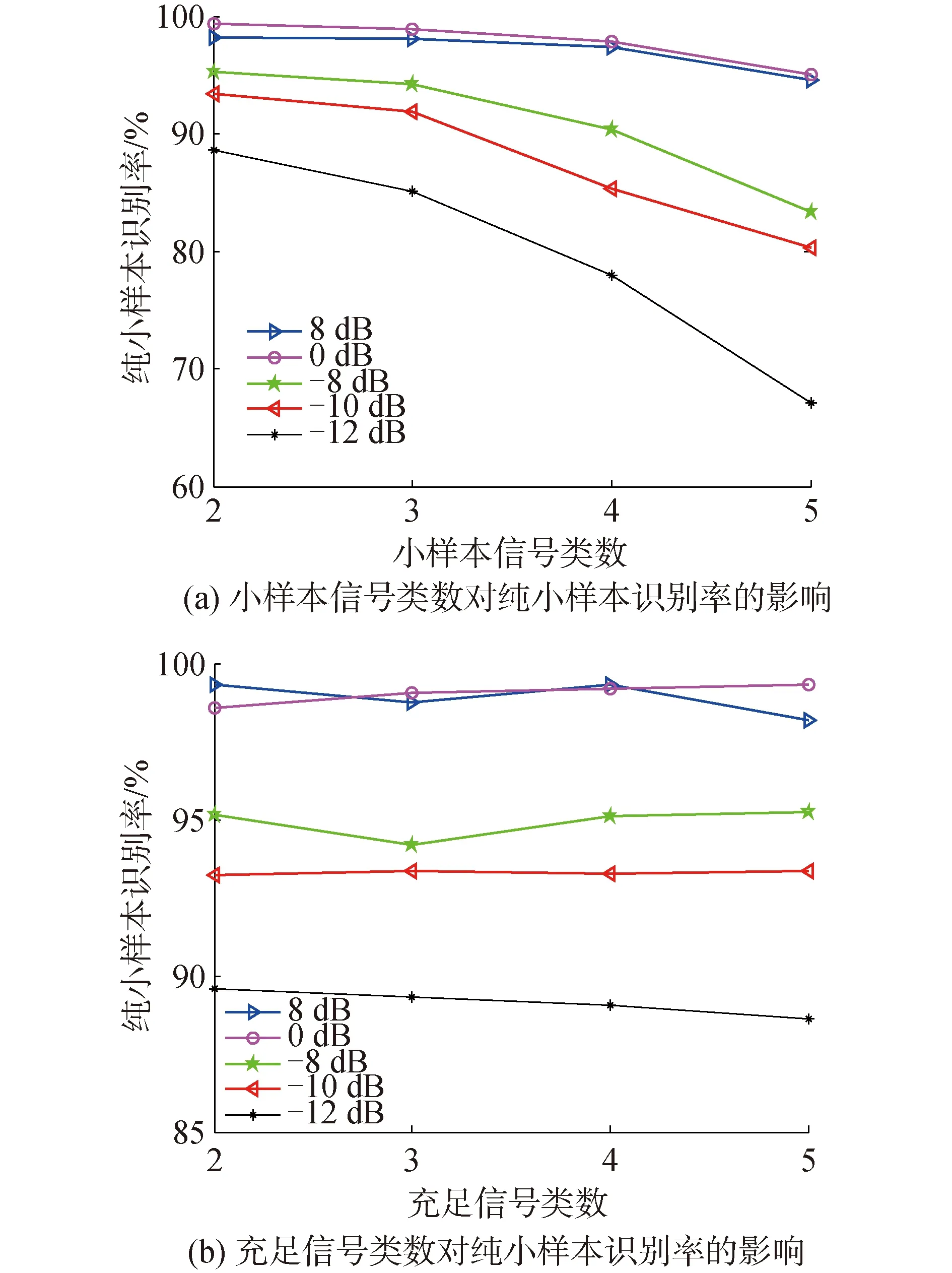
图9 充足、小样本类数的相对关系对纯小样本识别率的影响

对于已经训练完成的模型，在测试时的正确率同样受测试支持集样本数量的影响。该类样本数量越大，则对模型的利用率越大，能更好地发挥模型的表征能力。保持其他各类参数变量不变(充足信号为5类，训练信号样本数量为800)，对该变量下不同数值大小做了统计分析，如图10所示。

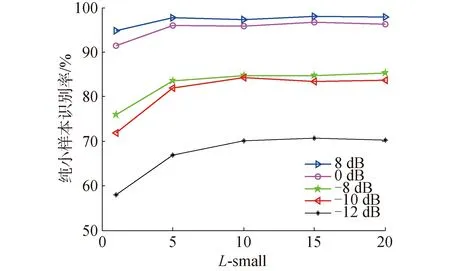
图10 小样本信号的小样本数对纯小样本识别率的影响

通过结果发现，在小样本区间[0～5]内，识别率与小样本数呈正相关，而超过5以后迟滞不变。实际中，小样本信号所提供的样本信息较少，符合小样本的思想。

6 结论

1)传统的雷达信号识别方法依赖雷达信号的大量样本数据以形成信号模板，对于有限的、少量的雷达信号数据缺乏有效的识别策略。

2)本文将雷达信号识别与深度学习中的原型网络结合，发挥原型网络在小样本训练中的优势，依靠已有的雷达信号数据库，不断优化样本类间距离，形成泛化的聚合模型。

3)捕捉有限的、少量的小样本雷达信号，就能识别出包括小样本雷达信号在内的所有LPI雷达信号。

4)仿真结果表明，等价样本信息条件下，AlexNet等普通有监督神经网络架构难以拟合出有效的训练模型，而本文提出的P-Net雷达信号识别算法能对小样本雷达信号达到较好的识别水准。