一种针对多用户通信的人工噪声鲁棒性优化方法
姚力, 刘友江, 张健
(1.中国工程物理研究院 电子工程研究所,四川 绵阳 621000; 2.电子科技大学 电子科学与工程学院,四川 成都 611731)
由于电磁波的广播特性,如何保证传输信息不被窃听成为了无线通信领域的关键问题。传统的无线通信保密一般采用密钥加密的形式,即发射端与接收端使用相同的或对称的密钥对明文进行加密解密运算的加密方法。但传统的密钥加密存在2个缺陷:1)密钥加密的保密性能高度依赖密钥的安全性,若密钥本身被窃听者截取或获得,则明文信息将完全暴露在窃听者面前;2)密钥加密一般以窃听者的计算能力来衡量密钥的加密性能,近年来,随着超级计算机技术的发展以及云计算等新技术的兴起,窃听者可以获得越来越强大的计算能力,使得原有的密钥可能无法确保信息安全,国内外的研究者们都在寻找一种能对密钥加密的2个缺陷进行补充的新加密方式,在这样的背景下,物理层安全的概念应运而生。物理层安全的思想最早来源于Shannon。Shannon[1]提出了 “完美保密”的概念,即通过某种编码形式,使得信源与编码后的码字相互独立,即可在不使用密钥的情况下,也能保证信息的安全。Wyner[2]基于Shannon的理论,证明了当合法信道的信道容量大于窃听信道的信道容量时,利用陪集编码的方式,发射端可以实现“完美保密”。进入21世纪后,由于多天线发射技术的迅猛发展,使发射端利用多天线自由度,构建优势信道成为可能。文献[3]研究由能量收集发射节点、目的节点和窃听节点组成的能量收集通信系统中,以最大化平均保密传输速率为目标的发送功率控制问题,文献[4]研究了基于Duffing振子阵列的四进制混沌接收机。与上述2篇文献的思路不同,文献[5]提出了利用人工噪声(artificial noise,AN)技术降低窃听者信道质量的方法。沿着这一思路,文献[6]研究了快衰落信道条件下AN的优化问题,文献[7]对慢衰落信道下,基于保密中断概率(secrecy outage probability,SOP)的AN优化问题进行了研究,文献[8]对SOP约束下,多用户多播信道的AN优化问题进行了研究。文献[9]通过神经网络,提出一种新的波束赋形(Beamforming,BF)方案。文献[10]针对退化高斯窃听信道下的物理层安全问题提出了一种基于极化码的物理层加密安全编码算法。文献[11]提出了一种针对不同重要度用户场景的最优化BF方案。
在传统的人工噪声相关研究中,一般假设发射端可以准确获取合法信道的信道状态信息(channel state information,CSI)。但在实际场景中,由于反馈信道的误差等原因,常常无法估计出准确的合法信道CSI,这就对发射端波束成形矩阵与AN算法的鲁棒性提出了更高的要求。过去的文献虽然也有关于发射端鲁棒性的研究,如文献[12]研究了认知无线电系统中AN算法的鲁棒性问题,而文献[13]研究了在安全服务质量限制下AN算法的鲁棒性问题,但对于多用户广播信道的安全通信,特别是慢衰落信道场景下,满足保密中断概率约束条件的多用户安全通信鲁棒性问题,现有的文献则鲜有涉及。
1 系统模型
本文针对一种慢衰落信道条件下,多用户多进单出单窃听(multiuser multi-input single-output single-eavesdropper,MU-MISOSE)保密通信系统,如图1所示。Alice为发射端,发射天线数为MT。Bob为单接收天线的合法用户,总用户数为K,其中Bob-k为第k个合法用户。为了保证足够的空间自由度以产生人工噪声,本文中假设MT>K。Eve为单天线窃听者,本文中假设Eve为被动窃听者,即Eve只进行窃听而不发射任何信号。
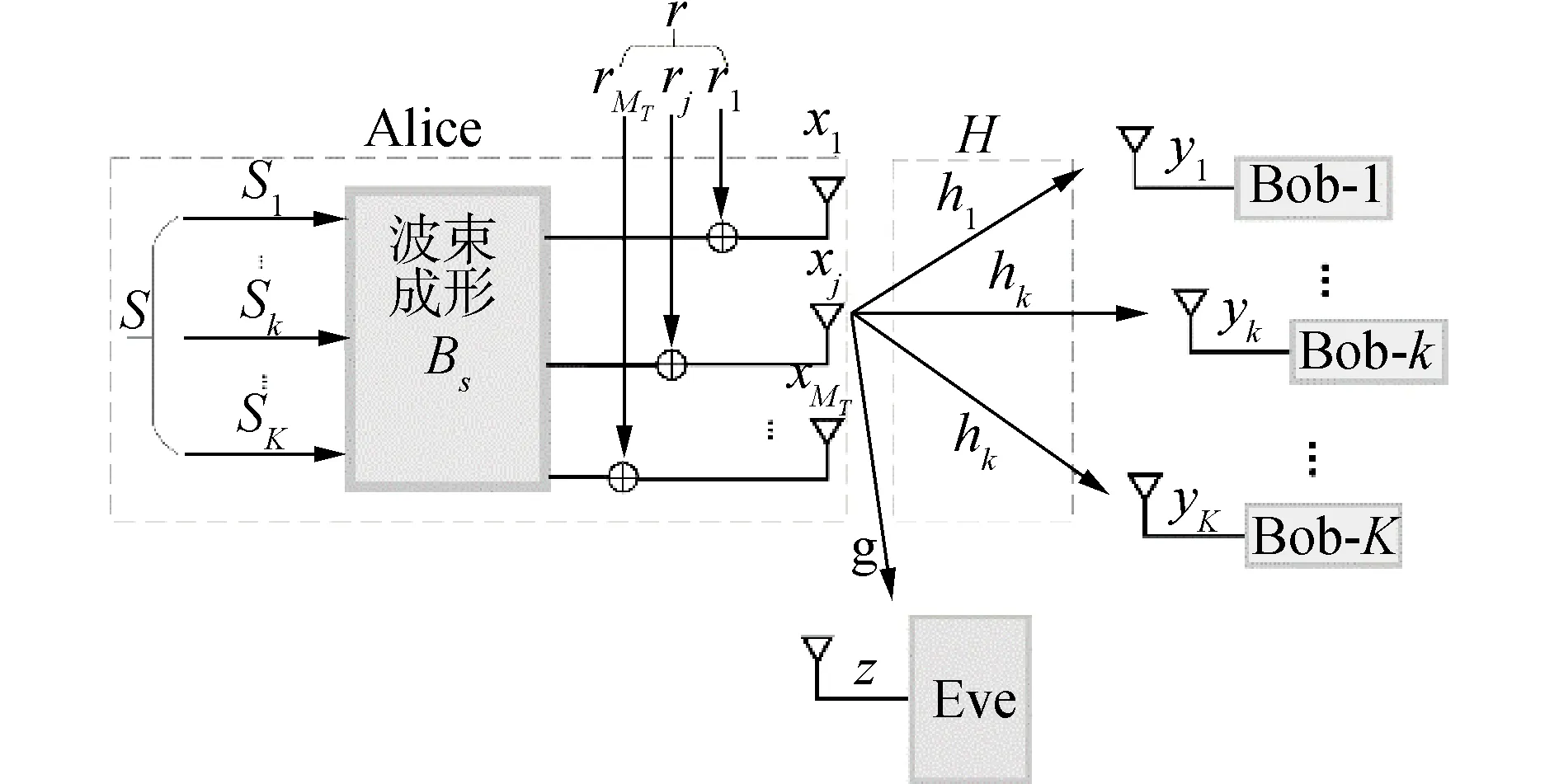
图1 MU-MISOSE保密通信系统模型
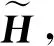
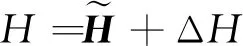
ΔH表示信道的估计误差。为了处理的简便,我们采用了常见的有界CSI误差模型,即:
(1)

由于Eve为被动窃听者,Alice难以获得其准确的信道信息。因此,本文中假设Alice只能获得窃听信道g的统计特性。此外,为了考虑最坏的情况,本文假设Eve可以准确地获取H与g。

x=Bs·s+r

在Bob-k的接收端,接收信号为:
yk=hk·Bs·s+hk·r+nk=
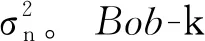
(2)

对于窃听端,本文中假设Eve尝试窃听某个其感兴趣的用户信号。由于Eve可以准确地获取H,故假设其可以完全消除用户间干扰,这种极端假设在过去的AN相关文献如[6-9]中常被使用,并且令信号安全通信更加难以实现。基于以上的假设,当Eve端窃听用户k的信息时,其接收信号为:
zk=g·bsk·sk+g·r+ne

(3)
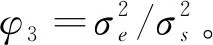
(4)
式中CBk=log(1+γBk)为用户k信道的信道容量;CEk=log(1+γEk)为Eve端窃听用户k的信息时,其信道的信道容量。
在慢衰落信道中,保密中断概率(secrecy outage probability,SOP)常被用于作为系统保密性能的量度。定义系统的SOP为:
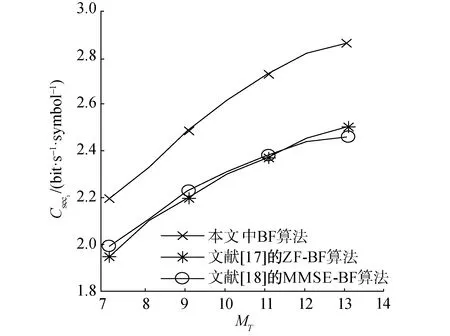
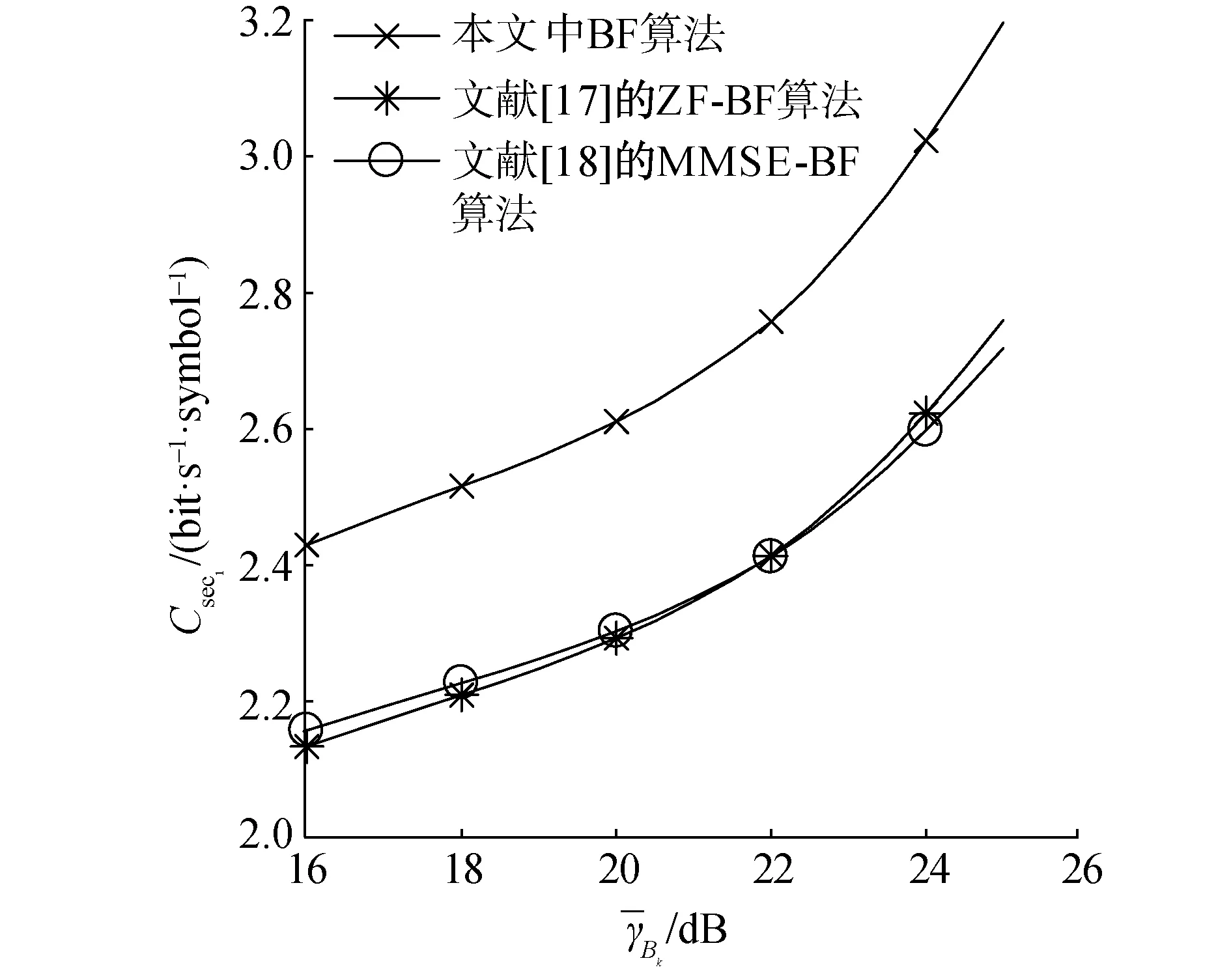
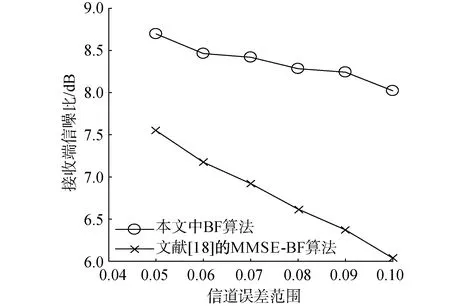
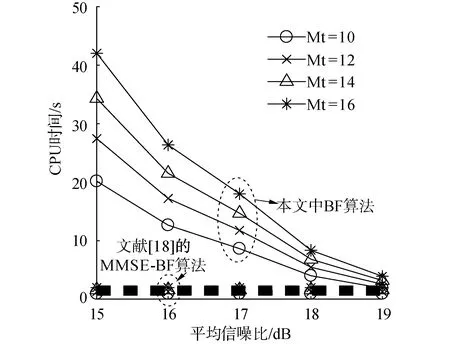
pout-k=Pr(Cseck (5) 式中RSk为信息信号sk的信息率。在本文中,我们希望设计一种在SOP限制与SINR限制下,使得K个用户中最小的RSk最大。这一问题可以表示为带约束条件的优化问题P1: (6) 式(6)为优化目标函数,式(7)为SOP约束,ε为预设的SOP约束常数。式(8)为SINR约束,γ为预设的SINR约束常数。式(9)为发射功率约束,式(10)保证优化变量为半正定矩阵。 显然,P1的约束条件皆为非凸函数。为了将非凸优化问题转化为容易处理的凸优化问题,将采用多种数学手段。 本节将对难以处理的非凸优化问题P1进行变换。首先处理SINR约束条件(8)。由于Alice无法获得准确的合法信道CSI,故式(8)中需要考虑信道估计误差ΔH。可以利用S-procedure来对式(8)进行变换: 引理1(S-procedure):如果有fk(x)=xAkxH+2Re(bkxH)+ck,k=1,2,Ak为n×n的Hermitian矩阵,bk为n×1的复向量,ck为实常数。则若要关系: f1(x)≤0→f2(x)≤0 成立,当且仅当存在一个常数η≥0,使得: 可将式(8)改写为: (11) (12) 式(12)可进一步展开为: (13) 因此,SINR约束条件式(8)可以被凸函数式(13)代替,优化问题P1可被改写为: (14) s.t.pout-k≤ε Bk0,Br0,ηk≥0 (15) 对于SOP约束条件式(7),可以使用文献[14]所提出的Bernstein-type不等式进行转化。 exp(-α) (16) 式中:λmax(A)为A矩阵最大的特征值。 为了应用引理2,令: RSk=log(1+γBk)-log(1+θk) (17) θk为新引入的中间变量。根据式(3)与式(4),SOP表达式式(5)可改写为: Pr(gBkgH-θkφ1gBrgH>θkφ3)= (18) α{λmax(Λk)}+}≤ε (19) 将式(19)与式(18)及SOP约束条件式(7)对比,可知若式(7)成立,需要满足: (20) 由于式(20)依然为非凸问题,故还需对式(20)做进一步处理。对于式(20)中的第1项Tr(Λk),可以转化为: Tr(Λk)=Tr[Bk-θk·φ1·Br]=Tr(Bk)-θk·φ1·Tr(Br) (21) 对于式(20)中的第2项,ΛkF可写作: ‖Λk‖F=‖Bk-θk·φ1·Br‖F≤ ‖Bk‖F+θk·φ1·‖Br‖F (22) 而: (23) 故: ‖Λk‖F≤Tr(Bk)+θk·φ1·‖Br‖F (24) 对于式(20)中的第3项,{λmax(Λk)}+可改为: {λmax(Λk)}+≤λmax(Bk)≤Tr(Bk) (25) 综合式(21)~(25),式(20)可近似为: (26) (27) (28) 结合式(17)、(28)有: (29) 由于γBk≥γ,故式(29)可近似为: 即: 1+γ≥t(1+θk) (30) 最终,可以将优化问题P2转化为优化问题P3: (31) Bk0,Br0,ηk≥0 1+γ≥t(1+θk) 然而由于Br、θk与t皆为优化变量,故约束条件式(26)与式(30)中都出现了非凸函数形式f(x,y)=xy。为了解决这一问题,如果θk为固定的常数,则式(26)与式(30)都将转变为凸函数;并且由于RSk为正,根据式(17),有θk<γ<γBk。因此,θk的最优解,可通过在(0,γ)范围内的一维线性搜索来获得。而当θk为常数时,优化问题P3可用现有的凸优化求解程序如CVX算法[15]来进行求解。 为了简化算法的计算复杂度,通过多次重复仿真,注意到对于不同用户,其最优的θk近似相等。故我们可以将K个变量θk简化为统一的变量θ。同时,我们注意到,当θ值较小时,优化问题P3无解,随着搜索算法的进行,θ值增大到某一值θ′时,优化问题P3开始有解,优化目标变量t取值为t′;当θ值继续增大,t值反而减小,即能够使得优化问题P3有解的最小θ值θ′即为最优解。这一现象可以通过P3中的约束条件进行解释,当θ值过小时,无法找到既能满足式(26)约束,同时满足式(9)约束的Bk与Br,故问题无解。而根据式(30),t与θ的乘积存在上界,当P3问题有解后,随着θ值继续增加,t值减小。故在搜索算法中第1个使P3有解的θ即为最优解。根据以上的分析,可以写出优化算法的流程: 1)设定: 系统常数MT、K、ε、γ、φ1、φ2、φ3、ψb以及步进常数τ。 2)输入: 3)初始化: 迭代指针n=1。 4)最优化: ▷ forθ=0:τ:γ 在固定的θ取值下,使用CVX算法,解决优化问题P3,获得对应的t(n),Bk(n),Br(n)。 判别t是否存在有效取值 如果是:跳出循环。当前的t(n)、θ(n)、Bk(n)、Br(n)即为问题的最优解; 如果否:继续循环。设定n=n+1。 ▷ end 通过上述中的算法流程获得最优的Bk-opt与Br-opt后,还需对其进行分解,获得最优的波束成形向量bsk及人工噪声向量r。由于无法保证Bk-opt与Br-opt为秩1矩阵,故无法对其直接做特征值分解。本文中采用文献[16]所提出的一种秩1近似法,以对Bk-opt的分解为例。令r为Bk-opt的秩,并令: 图2 不同发射天线数MT情况下,本文算法与传统波束成形算法保密容量Csec1的对比 图3 不同平均信噪比情况下,本文算法与传统波束成形算法保密容量Csec1的对比 图4 不同信道误差范围情况下,本文算法与MMSE算法接收端信噪比的对比 图5 本文算法与MMSE算法关于算法[18]复杂度的对比 1)本文将用以传输信息信号的波束赋形矩阵与用以干扰窃听者的人工噪声信号同时作为优化变量进行求解,设计出更加适合误差信道场景的预编码方案。 2)为了解决求解过程中复杂的非凸优化问题,本文采用了多种优化方法,对优化问题进行转化或近似,使其转化为易于求解的凸优化问题,并设计了一种全新的一维线性搜索算法。 3)在仿真验证部分,本文考察了不同系统参数对于算法性能的影响,并将提出的新设计方案与传统的发射方案作对比,证明了新设计方案在误差信道条件下具有更强的传输与保密性能。2 优化方法
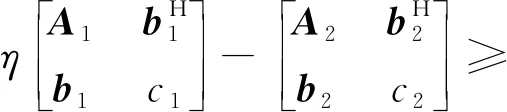
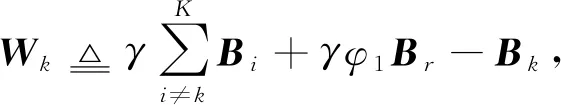
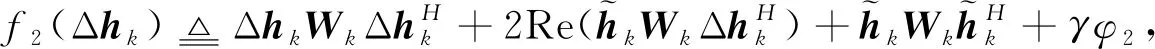
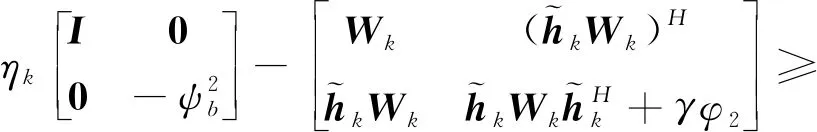




3 仿真验证


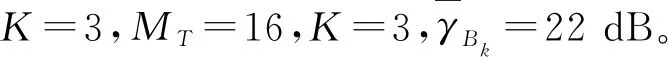
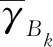

4 结论

