初高中教学的有效衔接

迟童心

【摘要】新时代课程改革背景下，初高中教学衔接的意义愈发凸显.函数内容在初中教材和高中教材中均有涉及，《普通高中数学课程标准（2017年版）》明确说明将函数纳入预备知识中.本文以函数内容为例，进行初高中教学衔接的研究，旨在帮助学生适应初中数学到高中数学的转变.

【关键词】函数;初高中;教学衔接

一、引言

新时代教育背景下，由于初中数学与高中数学的层次不同、跨度较大、侧重点不一致、抽象性差异等原因导致学生在高中数学学习阶段数学思维很难转变，对于新的知识内容无法准确理解.很多高中教师也反映学生的基础知识不够扎实，数学核心素养的形成不够完善.这对于教师的教学工作来说无疑是严峻的挑战.因此，初高中的衔接问题也成为教育界乃至社会各界广泛关注的重点.

函数通过构建模型来刻画现实世界的数量关系，进而通过对数量关系的探索解释现实世界，这体现在数学、物理等多个学科以及各个领域中.函数内容作为数学学习的主线之一贯串学生的整个初中、高中、大学以及研究生的学习阶段.函数与初高中数学中的方程、不等式有着十分密切的联系.因此，函数内容对于中学阶段数学学习的关键是不言而喻的，而函数概念作为函数知识内容的基础也是函数内容的核心，它的关键作用更加突出.

函数已经成为初高中数学的重要纽带之一.从初中到高中的学习阶段，函数部分由浅入深、层层递进，高中阶段的部分函数相关知识内容建立在初中阶段的基础上，做好初高中教学的衔接对函数部分的学习有着至关重要的作用.

二、初高中教学不易衔接的原因

（一）初高中学生认知发展不同

初中学生和高中学生相比无论是信息加工处理、空间想象能力，还是思维整体结构发展都具有不同的阶段性发展特征.因此，高中阶段的数学学习更加抽象化、复杂化，比较脱离生活实际.而高中函数的学习是在高一阶段，这个时候学生处于由一个阶段向另一个阶段发展的过程中，但各种认知水平还没有完全达到标准.初中学生处于具体运算阶段，思维的进行很难脱离具体事物的支持，逻辑结构比较单一.高中学生已经进入了形式运算阶段，思维水平相对进入了新的阶段，而这一阶段学生的表现就是逻辑思维进入高级阶段，抽象能力得到提升.此外，每个人的认知发展具有差异性，若学生的认知发展水平较差，或者是抽象能力不足、想象力不够等，都会影响初高中课程衔接的连贯性，尤其函数这一部分知识很难借助具体事物或者生活实例帮助学生理解.

（二）高中教师对初中教材了解程度不够

由于各种原因，不少高中数学教师并没有承担过初中数学课程讲解的任务，而且，许多高中数学教师并没有系统研究过初中数学的教材，从而使得这部分教师对于刚刚升入高中的学生的数学基础非常陌生，不了解学生在初中形成的数学思想方法以及学生思维发展程度.将原本为整体状态的数学知识内容分裂成两个部分对学生进行教学，会让学生在进入新的学习阶段后很难利用初中的数学知识作基础.数学知识不连贯，就无法形成整体的数学知识系统.甚至，初中数学没有学习的知识点有的老师也一笔带过，变成了学生的知识盲区.这部分老师将初中数学阶段和高中数学阶段完全分散，进入了一个只要将高中数学知识完全传授给学生就可以提高学生数学成绩的误区.事实上，这样的高中教师忽略了数学学科的整体性、思想上的一致性，更不符合高中数学课程标准中强调的基本理念之一——聚焦学生数学学科核心素养的形成，这对于初高中教学的衔接是非常不利的.只有高中教师熟悉学生初中的数学知识内容、整体框架结构、具体思想方法，再换位到学生的立场和知识积累状态去向学生传授高中数学知识内容，才能够达到初高中教学有效衔接的目标.

（三）初高中数学教学方法不同

和高中数学学习阶段相比，初中学习阶段的数学学习任务较少，教学进度较慢，教师有充分的时间和精力带领学生进行学习.细抠难点，重复重点，习题巩固，再加上初中阶段的习题类型一致，思想方法比较单一，学生经过大量的练习后很容易掌握数学知识内容.而高中阶段教学进度很快，教师重点在知识的引入、思想方法的形成、核心素养的建立，如果学生想要通过大量的练习来提升成绩是不现实的，这就对学生建立数学思想体系提出了新的要求.

（四）函数概念的发展历史

函数一词最早是由“function”一词转译而来，最早出现于数学家李善兰的《代数学》中.李善兰认为“函”可以表达出“包含”的意思，书中的函数指的是变量的意思.在17世纪时伽利略在他的著作《两门新科学》中突出了函数和变量的思想.17世纪时牛顿也抽离出了函数的思想，这里他用“流量”来表示变量关系.18世纪时约翰·伯努利将函数进行定义，他认为只要是变量x和常量所构成的等式都可以称之为函数，并对函数的表示方法进行了突出强调.在18世纪时欧拉也在其著作中将函数进行重新定义，他对函数的定义强调的是前面的量随着后面的量的变化而变化的依赖关系.到了19世纪的1821年，柯西对于函数概念部分进行了进一步的探究，他不仅在前人的基础上对函数的概念进行了更严密的定义，而且给出了自变量的定义.历史上首次提出自变量的定义的就是柯西.就在第二年，傅里叶提出了有关函数问题的新思路，他发现函数可以用曲线来表示，可以用某个单一式子来表示，也可以用多个复合式子来表示.这一发现使函数概念的研究又进一步深入.1837年狄利克雷提出了经典的函数概念，他对函数的依赖关系进行淡化，指出：“对于在某个区间上任一确定的x值，都有一个确定的y值和它对应，那么y叫作x的函数.”这个函数的全新定义用更清晰的语言去描述函数，也更容易被大众所接受.1921年库拉托夫斯基用集合的概念来定义函数，使得函数概念更加严密、严谨.1930年是这样对函数进行重新定义的：“若对集合M的任意元素x，总有集合N确定的元素y与之对应，则称在集合M上定义一个函数，记为y=f（x）.元素x称为自變量，元素y称为因变量.”这是函数概念的现代定义，这与今天我们在课本上学习的函数概念内容基本类似.D2357F07-1EC1-47E7-916D-2212900B0125

函数概念历经三个世纪的发展才逐渐完备，贯串古今，旷日持久.研究表明，中学生对于函数概念的定义方式与历史上对函数的定义具有很强的相似性.学生对于函数的认识过程与科学家们在历史上对于函数的认识过程十分贴近.这就说明在学习函数概念时，了解函数概念的历史发展会帮助学生掌握函数概念的本质.

三、初高中函数内容的区别和联系

（一）初高中函数概念的区别

初中和高中阶段的函数概念具有不同的表示方法.初中阶段函数概念属于描述性定义，强调变量之间的相互联系，以运动的观点进行探究，以自变量x和因变量y来定义函数概念，生动，立体，形象，贴近生活实际，使初中阶段的学生容易理解.高中阶段函数的概念是建立在集合知识基础之上的，强调定义域、值域，以及对应法则，通过设定两个特殊的集合，再根据函数的对应关系进行定义.集合的知识内容较为抽象，代表性不强，学生不易理解.

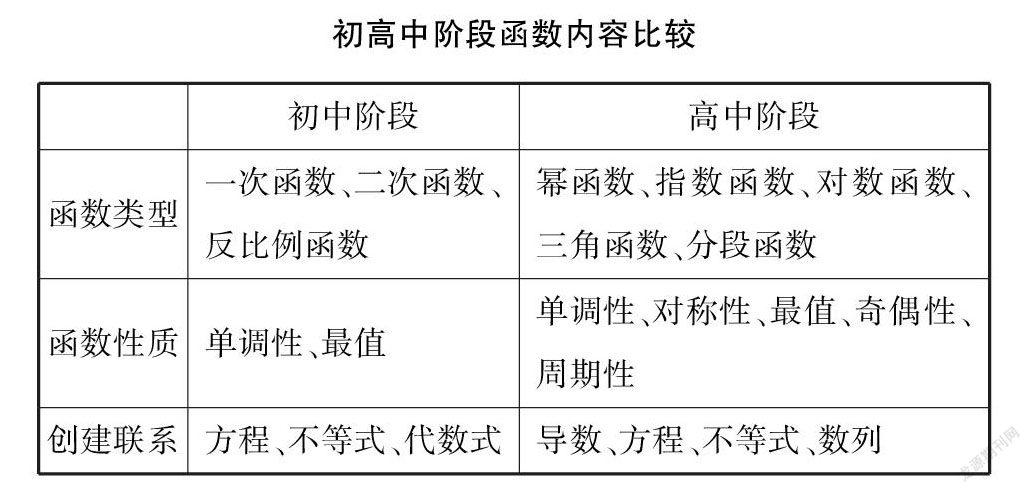
上表对于函数知识在初高中的不同进行了对比，可以明显地看出初中阶段的函数内容更加简单，所研究的函数类型比较单一，函数性质的涉猎也比较少.高中阶段的函数内容无论是函数性质、函数类型还是函数与其他知识内容的联系都比较深奥复杂.

（二）初高中函数教学目标的区别

无论是从初高中学生的思维发展阶段不同来说，还是从初高中知识的考查侧重方向不同来说，初中和高中阶段函数内容的教学目标都不一致，这一点从课程标准上可以充分体现.《义务教育数学课程标准（2011年版）》中对函数内容的要求侧重对常量以及变量的情况分析.《普通高中数学课程标准（2017版）》中对函数内容的要求是以提升数学核心素养为背景，重视变量的对应关系，同时，对函数性质的掌握也做出了要求.

（三）初高中函数教材呈现方式的区别

初高中教材中函数内容为便于学生的理解都是从具体生活实例中进行归纳，但呈现的方式具有不同的特征.比如，初中教材中函数部分更多的是以文字介绍，而高中教材中函数部分主要使用符号语言.再如，初中教材中函数部分知识内容较少，而高中阶段在了解函数概念后对于函数的几个重要性质进行了深入研究.

（四）初高中函数内容的联系

初中与高中函数内容的学习是螺旋式上升的过程，虽然侧重点不同，但是实质是相同的，并且它们在应用过程中经常将数与图形的对应关系相联系，也就是经常采用数形结合的方法，这是研究探讨函数性质过程中最为清晰直观的方法.在函数性质中，函数的单调性这一性质是在高中教材中给出的，但是函数变化增减的思想早在初中阶段的学习过程中就有涉猎，初中阶段用y随着x的增大而增大这样的语言去描述函数变化特征.函数内容其实是一个整体的数学知识内容，只是在初中和高中的不同阶段，我们根据学生的不同思想发展水平用不同的数学语言去描述和形容，但究其本质其实是相同的.初中函数内容和高中函数内容是相互渗透、相互作用的关系.

四、初高中函数部分教学衔接具体实例

（一）有关函数概念引入的衔接

在高中引入函数概念之前，学生已经在初中就掌握了从运动变化的角度所归纳的函数概念.因此，教师可以通过提问复习的方式帮助学生唤醒初中阶段的较为直观的函数概念，以加强初高中函数概念的联系.接著，教师可以通过实例创设问题情境，举例如下：

例1 小明到某文具店去采购笔记本，每本的价格为3元，设小明买了x本，购买笔记本共花费了y元.

此函数的解析式为y=3x（x≥0），重点强调函数的定义域.我们进一步设疑：此函数与y=3x是相同函数吗？这样的做法打破初中函数学习的局限，使学生通过实际问题认识到初高中函数部分的区别和联系.教师引导学生通过集合的表达方式，以对应关系为背景建立高中函数知识体系，对比初高中函数的不同使学生对高中函数产生疑问，进一步激发学生的学习兴趣.

（二）有关函数性质的衔接

高中数学中不少函数内容的分析都采用了数形结合的方法，而在初中阶段其实也有很多关于数形结合思想的渗透.比如，对于函数y=ax2+bx+c，若a>0，则开口向上;若a<0，则开口向下.这给学生在高中数学中函数内容的学习建立了思想基础.高中函数易引导学生思考研究未知系数a，b，c对方程的影响，尤其是在幂函数y=xa、指数函数y=ax（a>0，且a≠1）、对数函数y=logax（a>0且a≠1）中探索研究|a|对函数图像的影响，以及研究二次函数中探索b值对函数图像（对称轴）的影响.教师应在初中所学内容的基础上进行教学，衔接初高中函数内容知识，建立系统的函数知识体系.

（三）有关函数习题的衔接

在初中阶段系统学习函数内容时，其实对函数的性质——单调性已经做了简单的阐述：“随着x增大，y逐渐增大”或者“随着x增大，y逐渐减小”.虽然没有像高中函数那样将性质进行抽象，运用符号语言进行描述，但是也体现出了单调性的核心思想.在初中学习函数内容时，教师可以通过练习题向学生渗透高中函数的思维方式.

例2 下列函数中，自变量x在什么范围内，y随着x的增大而增大？自变量x在什么范围内，y随着x的增大而减小？

（1）y=3x2-6x+3;

（2）y=-2x-6;

（3）y=8x;

（4）如下图所示.

在初中阶段编排此类习题具有两方面的意义：一方面，（1）（2）（3）分别是二次函数、一次函数、反比例函数，考查它们的目的是使学生巩固函数的单调性，为高中学习函数的单调性打下坚实的基础，帮助高中阶段的学生形成全面深化的知识体系和思维体系.另一方面，（4）可以拓展学生的知识领域，与高中函数内容进行衔接.这个特殊的分段函数需要学生针对不同的x的取值范围进行讨论，在这里高中函数思想得到渗透，从而能帮助学生的知识体系向上兼容.

五、结束语

函数内容作为中学阶段数学学习的主线之一，无论是中考还是高考都有重要占比.初高中函数教学衔接对于初中阶段学生或高中阶段学生的知识掌握都具有重要意义.第一，将初高中内容进行衔接有助于学生整体把握

函数内容，将函数内容形成系统的知识体系，有助于学生建立数学思想方法.第二，将高中数学函数内容涉猎的数学思想渗透进初中数学中，对学生的数学思维的立体化形成具有深刻意义.初高中函数教学衔接对初中学生来说不仅可以拓展其数学思维，还给中考的拉分题提供了思路.第三，不少初中生在进入高中后，表示很难充分掌握高中数学中比较抽象的知识内容，对高中数学的思维方式不适应，而有效地衔接初高中数学内容无疑能解决这部分学生的问题.

【参考文献】

[1]邓勤. 新课程背景下初高中数学教学的有效衔接：从函数概念的教学谈起[J].数学通报， 2011（2）：33-35.

[2]佟震. 关于初高中数学衔接的思考：以高中二次函数教学为例[J].数学学习与研究，2017（11）：40.

[3]秦萍萍. 新课标下高中函数概念的教学研究：以海南师范大学附属中学为例[D]. 海口：海南师范大学， 2014.

[4]孙明侠. 新课程下高考中函数概念的易错点剖析[J]. 吉林省教育学院学报， 2016（7）：7-10.D2357F07-1EC1-47E7-916D-2212900B0125