非局部扩散三种群竞争系统的双稳行波解的Lyapunov稳定性

张国宝，郝玉财

(西北师范大学 数学与统计学院,甘肃 兰州 730070)

研究具有非局部扩散的三种群Lotka-Volterra竞争系统[1-2]

(1)

其中,u(x,t),v(x,t),w(x,t)分别表示三个种群在空间位置x和时刻t的种群密度,bij>0是种群j和种群i之间的竞争系数,ri>0是种群i的自然增长率,di>0是种群i的扩散系数,Ji是种群i的迁徙率.为了简单起见,通过时间和空间尺度变换,将各种群的环境承载力标准化为1.Ji*υ-υ称为非局部扩散算子,表示长距离的扩散机制,其中Ji*υ是R上的标准空间卷积,即

由系统(1)可见，种群v和种群w对食物资源有不同的偏好，即种群v和w之间没有竞争，但是,种群u与种群v,w都存在竞争关系.核函数Ji可以看作概率密度函数.假设核函数Ji和系统(1)的竞争系数满足以下条件:

(H1)Ji∈C(R),Ji(x)=Ji(-x)≥0,且

(H3)01.

条件(H3)表明种群v和w相对于种群u是弱竞争者,但将种群v和w放在一起可能会在与种群u的竞争中胜出.

非局部扩散系统存在于许多应用学科,如种群生态学、流行病学、相变以及神经网络模型等[3-7].系统(1)是如下具有随机扩散的Lotka-Volterra竞争系统的非局部扩散情形:

(2)

显然,系统(1)和系统(2)对应的空间齐次系统为

(3)

常微分方程系统(3)有一个平凡平衡点(0,0,0),4个半平凡平衡点(1,0,0),(0,1,0),(0,0,1),(0,1,1)以及一个正平衡点(u*,v*,w*),其中，

由条件(H3)可知,常数平衡点(0,1,1)和(1,0,0)是线性稳定的,其他平衡点是不稳定的，因此,该系统具有双稳非线性.假定目前的生态系统中已有种群v和w,现在引入新的种群u，一个很自然的问题是哪个种群将在竞争中获胜?为了回答这个问题,我们研究系统(1)的连接平衡点(0,1,1)和(1,0,0)的行波解.

系统(1)的行波解具有形式

(u,v,w)(x,t)=(φ,ψ,φ)(x+ct),

(4)

其中,x∈R,t≥0,c∈R是非零传播速度.将(4)式代入(1)式,可得系统(1)的波廓系统为

其中,ξ:=x+ct，且

基于对入侵者u的入侵过程的兴趣,(φ,ψ,φ)满足如下边界条件：

2017年，在b21>1,b31>1,b12+b13<1的假设下,Dong等[8]建立了系统(1)的连接平衡点(0,1,1)和(1,0,0)的单稳行波解的存在性和渐近行为，Zhang等[2]进一步研究了系统(1)的单稳行波解的唯一性和稳定性.最近,He等[9]考虑了系统(1)的行波解的最小波速,并给出了最小波速线性抉择的条件.特别地,Dong等[1]研究了系统(1)具有非局部各向异性扩散的双稳行波解，他们首先通过截断问题的极限论证建立了行波解的存在性和单调性,然后利用Ikehara引理得到了行波解的渐近行为,并在此基础上研究了波廓和波速的唯一性.到目前为止,系统(1)的双稳行波解的稳定性依然是未知的，因此,文中主要研究系统(1)的双稳行波解的稳定性.

1 预备知识和主要结论

(5)

其中,x∈R,t>0,且f1,f2,f3定义如下:

显然,在区域{(u,v,w)：u≥0,v≤1,w≤1}中,f1,f2,f3满足如下条件:

同时,系统(5)对应的行波解(φ,ψ,φ)满足

(6)

且具有渐近边界条件

命题1[1]假定条件(H1)～(H3)成立,则系统(5)存在连接平衡点(0,0,0)和(1,1,1)的波速为c∈R的非降行波解(φ,ψ,φ)(x+ct)，且上述双稳行波解在c≠0时是严格单调的.

定理1(Lyapunov稳定性) 假定条件(H1)～(H3)成立,(φ,ψ,φ)(x+ct)是系统(5)的双稳行波解,其中c≠0.设(u,v,w)(x,t)是系统(5)的具有初值(u,v,w)(x,0)=(u0,v0,w0)(x)的解,其中

则(φ,ψ,φ)(x+ct)是Lyapunov稳定的.即对任意的ε>0,存在常数γ>0,若

||(u0,v0,w0)(·)-(φ,ψ,φ)(·)||<γ

(9)

成立,则

2 Lyapunov稳定性

本节利用上下解方法研究系统(5)的具有非零波速的双稳行波解的Lyapunov稳定性.

定义1假定函数(u+,v+,w+)满足

(11)

其中,x∈R,t>0,则(u+,v+,w+)称为系统(5)的上解.类似地,通过改变不等号的方向可以定义系统(5)的下解.

设E-和E+分别是f1,f2,f3在(0,0,0)和(1,1,1)处的Jacobi矩阵,即

λ±=max{Reλ:λ∈σ(M±)}<0,

(12)

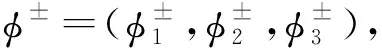
M±φ±=λ±φ±.

(13)

设E=∂(f1,f2,f3)/∂(u,v,w)是取值于(u,v,w)处的Jacobi矩阵.若取ν>0足够小,则

由(7)式可知,存在ξ1=ξ1(ν)>0,使得

定义函数

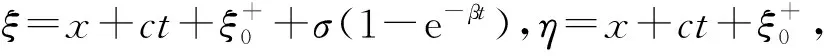
由(6)式可得

Γ(x,t)=σe-βt(βφ′(ξ)+δ(I1-I2)),

其中

取

由(18)和(19)式可知,存在常数ξ2>0,使得

接下来证明:对任意的(x,t)∈R×[0,+∞)和σ>0,若δ足够小,则Γ(x,t)≥0.令ξ0:=max{ξ1,ξ2+1},并且假设δ0≤ν/2σ.分以下三种情形进行讨论:

情形1η>ξ0.在此情形下,η>ξ2+1,因此,由(22)和(23)式可得

显然,ξ≥η>ξ1,所以由(17)式可知

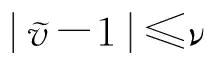
由(13),(15)和(22)式可得

因此

情形2η<-ξ0.和情形1类似地讨论可知Γ(x,t)≥0.

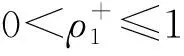
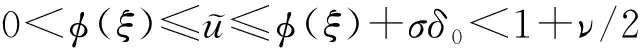
显然L3仅依赖于v.进一步有I2≤3L3.

定义

则

因此Γ(x,t)≥0只需取δ0≤βL4/(|c|+L1+3L3).因此,(11)式的第一个不等式成立.

同理可证其他不等式也成立.】

定理1的证明令

再由(9)式可得

其中,x∈R,t≥0.因此,由比较原理可得

这说明|u(x,t)-φ(x+ct)|<2σL5.因此,由σ=ε/(2L5)可得

||u(·,t)-φ(·)||<2σL5=ε.

同理可证

综上，定理1自然成立.】