一类带齐次凝聚核的Smoluchowski方程的尺度变换群及相似解

林府标,杨欣霞,张千宏

(贵州财经大学 数学与统计学院,贵州 贵阳 550025)

0 引言

1917年,统计物理学家Smoluchowski提出的Smoluchowski方程[1]，尽管精确解探寻困难，但其数值解却不断涌现，应用广泛[2-9]，如气或水溶胶科学、大气科学、云科学、工业环保科学、环境力学、纳米颗粒综合工程科学等.连续型积分-偏微分Smoluchowski方程可写成

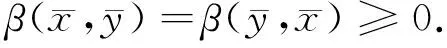
(2)

凝聚是指两个粒子成功碰撞聚并成一个质量较大的粒子.一对实体粒子发生碰撞的概率及碰撞之后的成功凝聚及反弹，是决定凝聚核的两个主要因素.凝聚核在气溶胶动力学、化学、物理学等诸多应用学科领域扮演着重要的角色.在纷繁复杂和类型多样的凝聚核中，γ次齐次凝聚核

(3)

以下是几类主要的凝聚核函数：

1)连续区布朗凝聚核函数[8]：

(5)

其中κ1=2kBT/(3μ)为碰撞系数，kB是玻耳兹曼(Boltzmann)常数，T是气体温度，μ是气体的粘性度.

2)自由分子区布朗凝聚核函数[8]：

(6)

其中κ2=(3/4π)1/6(6kBT/ρp)1/2为碰撞系数，kB是玻耳兹曼(Boltzmann)常数，T是气体温度，ρp是粒子密度.

3)剪切凝聚核函数[6]：

(7)

4)纯热泳凝聚核函数[9]：

其中Cs,Ct,Cm是气体-固体相互作用系数,A1是密立根(Millikan)滑移修正因子,ν是气体运动粘度，kg是气体导热系数，kp是粒子导热系数，T是局部气体温度，T是温度梯度，l是气体平均自由程.

近年来，探究积分-偏微分方程(1)的解及解法已受到国内外诸多学者的关注[2-9]，鉴于其精确解极度匮乏，常常需要借助数值离散方案、数值实验、近似解析逼近理论等方法.在工程应用领域，解析研究带最简单凝聚核的积分-偏微分方程(1)对应的初值及边值问题，往往都是既棘手又重要的课题.针对一般的凝聚核(2)，寻找积分-偏微分方程(1)的显式精确解及解法技巧是非常困难的，需要数学方法的重大创新或突破.

其中N0代表核滴的初始数量,p为常数，而一阶矩V代表空间单位体积被浓缩成水的体积.

2014年，Yu等[3]利用矩泰勒展式讨论了带凝聚核(6)的积分-偏微分方程(1)的解析解；2006年，Fournier等[4]分析了带凝聚核(7)和(8)的积分-偏微分方程(1)的测度值解的存在性和唯一性；2000年，Ramkrishna[5]研究了积分-偏微分方程(1)的相似行为和自相似解;1965年，Friedlander等[6]用相似变换得到了群体平衡方程的自保持分布的渐近形式解.近年来，林府标等[13]采用伸缩变换群分析法寻找带常数凝聚核、和凝聚核、乘积凝聚核的积分-偏微分方程(1)的相似解，Lin等[14]利用尺度变换群结合改进的李群分析法探寻群体平衡方程的精确解，文献[7-9]应用几何平均近似法、广义对数正态矩法、对数正态矩法等探讨了带凝聚核(5),(6)和(8)的积分-偏微分方程(1)的解析解.

受上述工作的启发，文中首先将量纲分析法应用于求解带齐次凝聚核(4)的积分-偏微分方程(1)，减少齐次凝聚核(5)～(8)中独立常量的数量，简化原方程带繁琐独立常量的复杂性；其次，将常用于函数、常微分方程、纯偏微分方程的尺度变换群分析法，用于带齐次凝聚核(4)的积分-偏微分方程(1)，尝试探究其有效性、可行性和简洁性，在不同于文献[5-6,13-14]的尺度变换群的作用下，用尺度函数的相似不变量构造自相似解和约化积分-常微分方程；最后，借助于带齐次凝聚核(4)的积分-偏微分方程(1)接受的平移变换群的平移作用和找到的自相似解，进一步构造原方程的新相似解.

1 量纲分析

量纲分析[10]在自然和工程科学有着广泛的应用领域，其基本理论来源于美国工程科学家 Buckingham，即所谓的Buckingham π-定理[11].机械工程、物理学等诸多实际问题中，往往需处理许多刻画自然现象本质的一些基本的量、控制参数及数量，如实验测量、长度、质量、时间等.量纲分析的主要思想，就是减少必不可少的相互独立的量的数量.

受文献[10,12-14]的启发，假设积分-偏微分方程(1)接受尺度变换系

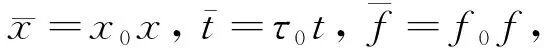
(9)

因此，带γ次齐次核函数(4)的积分-偏微分方程(1)可重新改写成

积分-偏微分方程(12)的初值和边值条件分别为

初值条件f(x,0)=0表示最初种群系统中没有粒子存在，边界条件f(∞,t)=0刻画尺寸足够大的粒子，种群粒度分布必然趋于零.

针对布朗凝聚核函数(5)，采用γ次齐次核函数的性质(4)可推出γ=0.若选取参数κ=κ1,f0=1/(κ1x0τ0)，则积分-偏微分方程(12)可写成

2 尺度变换群分析

假设积分-偏微分方程(12)接受单参数尺度变换群

借助假设条件可知,尺度变换群(18)将积分-偏微分方程(12)的任一解f=f(x,t)变换成积分-偏微分方程

的解.把解的表达式

及尺度变换群(18)代入积分-偏微分方程(19)，得到

鉴于f=f(x,t)是积分-偏微分方程(12)的任一解，由积分-偏微分方程(20)，可推出尺度变换群(18)所含参数λ1和λ2满足恒等式

μ=-(γ+1)λ1-λ2.

(21)

借助于量纲分析和尺度变换群的算法框架，研究积分-偏微分方程(12).鉴于因变量个数m=1，自变量个数n=2，尺度变换群的参数个数r=1,于是m+n-r=2，所以存在两个相互独立的尺度函数相似不变量

其中θ1i,θ2i,θ3i(i=1,2)为未知实常数.若要使尺度函数相似不变量(22)在尺度变换群(18)的作用下仍然保持为不变量，则有

将尺度变换群(18)代入尺度函数相似不变量恒等方程，得到

由群参数a的任意性，得到

把关系式(21)代入方程(23)，得到

3 解的群变换及相似解

类似于尺度变换群(18)被积分-偏微分方程(12)接受的证明方法，可验证积分-偏微分方程(12)接受单参数平移变换群

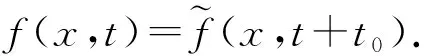
将解向量(25)代入(22)式，于是相互独立的尺度函数的相似不变量φ1和φ2可写成

φ1(x,t,f)=tf,φ2(x,t,f)=x.

借助于平移变换群Tt0的平移作用,带γ次齐次核函数(4)的积分-偏微分方程(12)的相似解可写成

f(x,t)=(t+t0)-1φ(x),

(26)

其中相似解(26)满足初值和边值条件(13)，函数φ(x)满足约化积分-常微分方程

若常数λ1≠0,令α=λ2/λ1,α∈R，则方程(24)可重新改写成

因此方程(28)的解向量为

将解向量(29)代入表达式(22)式，于是相互独立的尺度函数的相似不变量φ1和φ1可写成

借助于平移变换群Tt0的平移作用,带γ次齐次核函数(4)的积分-偏微分方程(12)的相似解可写成

f(x,t)=x-1-γ-αφ(z),z=x-α(t+t0),

(30)

其中相似解(30)满足初值和边值条件(13)，函数φ(z)满足约化积分-常微分方程

3.1 情形

针对布朗凝聚核函数(5)，用齐次核函数的性质(4)可得γ=0.结合相似解(26)和约化方程(27)，积分-偏微分方程(12)的相似解可写成

f(x,t)=(x+t0)-1φ(x),

其中函数φ(x)满足约化积分-常微分方程

类似地，结合相似解(30)和约化方程(31)，积分-偏微分方程(12)的相似解可写成

f(x,t)=x-1-αφ(z),z=x-α(t+t0),

其中函数φ(z)满足约化积分-常微分方程

3.2 情形

针对布朗凝聚核函数(6)，采用齐次核函数的性质(4)可得γ=1/6.结合相似解(26)和约化程(27)，积分-偏微分方程(12)的相似解可写成

f(x,t)=(x+t0)-1φ(x),

其中函数φ(x)满足约化积分-常微分方程

类似地，结合相似解(30)和约化方程(31)，积分-偏微分方程(12)的相似解可写成

其中函数φ(z)满足约化积分-常微分方程

3.3 情形

针对剪切凝聚核函数(7)，用齐次核函数的性质(4)可推出γ=1.结合相似解(26)和约化方程(27)，积分-偏微分方程(12)的相似解可写成

f(x,t)=(x+t0)-1φ(x),

其中函数φ(x)满足约化积分-常微分方程

类似地,结合相似解(30)和约化方程(31),积分-偏微分方程(12)的相似解可写成

f(x,t)=x-2-αφ(z),z=x-α(t+t0),

其中函数φ(z)满足约化积分-常微分方程

3.4 情形

针对纯热泳凝聚核函数(8)，用齐次核函数的性质(4)可得γ=1/3.结合相似解(26)和约化方程(27)，积分-偏微分方程(12)的相似解可写成

f(x,t)=(x+t0)-1φ(x),

其中函数φ(x)满足约化积分-常微分方程

类似地,结合相似解(30)和约化方程(31)，积分-偏微分方程(12)的相似解可写成

其中函数φ(z)满足约化积分-常微分方程

4 结束语

探究带齐次凝聚核的积分-偏微分群体平衡Smoluchowski方程的精确解及解法，在理论和实际应用上均是重要的研究课题，精确解可以很好地描述和刻画实体问题的本质规律.文中用量纲分析、尺度变换群和解的群变换技巧研究方程的相似解，并且用尺度函数的相似不变量构造相似解，丰富了精确解的多样性.如何获得约化的积分-常微分方程的精确解以及相似解与高精度数值解的误差，从而判断该相似解的精确程度与潜在应用价值，值得在今后的研究中深思和探究.