移位Bernstein多项式算法对粘弹性梁的数值分析

金素花，解加全，韩存弟，孙虹霞，陈一鸣

(1.燕山大学 理学院，河北 秦皇岛 066004；2.太原师范学院 数学系，山西 晋中 030619；3.太原理工大学 先进成形与智能装备研究院，山西 太原 030024 )

0 引言

粘弹性材料是介于理想粘性和理想弹性之间的一种材料，由于其具有良好的吸噪和减振性能[1-3]，所以在工程实践中得到了广泛应用.混凝土是生活中常见的一种粘弹性材料，经常被用于道路工程.随着粘弹性材料的逐渐发展，变分数阶模型得到了广泛的研究.相较于整数阶和分数阶模型，变分阶模型可以利用较少的参数去描述动态粘弹性行为.在大变形条件下，变分数阶微分算子比分数阶微分算子能更准确地模拟粘弹性材料的本构关系[4].为了准确描述非晶玻璃态聚合物的压缩变形，Meng等[5]提出了变分数阶本构模型，Li等[6]提出了一种变分数阶模型来描述形状记忆聚合物的粘弹性特性，并与分数阶模型进行比较，证明了变分数阶微分方程模型比分数阶微分方程模型更适合于形状记忆聚合物的记忆行为建模.

变分数阶模型的研究不仅包含模型的建立，还包含模型的计算.变分数阶粘弹性模型的研究主要有Adomian方法[7]、同伦摄动法[8]、同伦分析法[9]、变分迭代法[10]和小波函数算子矩阵分析法[11,12]等.由于变分数阶偏微分方程的阶数会随着自变量时刻发生变化，这种不稳定性极大增加了求解方程的难度，目前已有的计算方法都存在计算步骤复杂和计算精度低等缺点.Bernstein多项式具有良好的稳定性和逼近性.Kadkhoda[13]利用Bernstein多项式求解了流体力学中线性变分数阶微分方程，Wang等[14]采用Bernstein多项式研究了两类时间分数阶广义五阶微分方程的数值解，Derakhshan等[15]提出了一种利用Bernstein多项式求解Caputo-Prabhakar意义下一类非线性变分数阶微分方程的数值方法.

两端固定梁作为一个经典的力学模型在工程中有着广泛的应用.近年来，梁的分数阶振动被广泛研究[16,17]，但是对于梁的变分数阶振动的研究几乎没有，文中建立了粘弹性梁的变分数阶位移控制方程，用移位Bernstein多项式求解变分数阶粘弹性微分方程的数值解，并结合数值模拟分析混凝土粘弹性梁的动力学行为.

1 预备知识

定义1变分数阶Coimbra微分为[18]

其中,t≥0,0<α(x) ≤1,α(x)是变分数阶函数，f(x,t)是连续函数，Γ是Gamma函数.

定义2变分数阶Caputo微分为[19]

当f(t)=xmtn时，有

当xm=1时，有

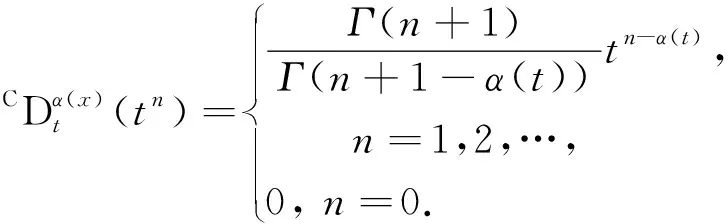
(4)

定义3在区间[0,1]上定义Bernstein多项式

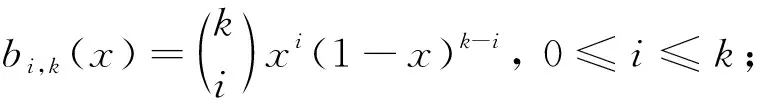
(5)

扩展x到区间[0,L]上，移位Bernstein多项式的通项公式为

用二项式定理展开(L-x)k-i，有

用一系列移位Bernstein多项式表示矩阵

其中，k为多项式的项数，且

P是可逆的，且Hk(x)=P-1φ(x).

2 控制方程的建立

考虑一个由粘弹性材料做成的梁，受到一个垂直于梁水平方向的外部载荷，使得梁发生形变，如图1所示.由于粘弹性材料的影响，其形变会发生一定程度上的恢复行为，因此，产生了垂直于梁水平方向的振动.两端固定梁的动力学方程为

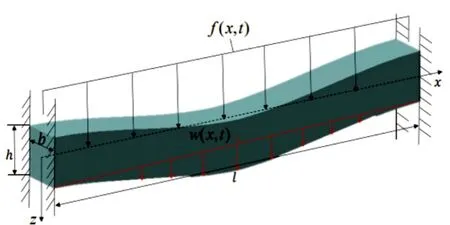
图1 两端横向固定梁的模型

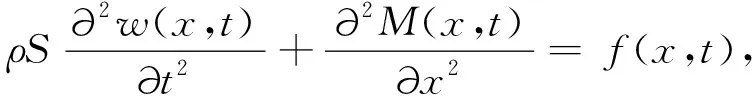
(11)

其中ρ是粘弹性材料的密度(kg/m3)，S是梁的横截面积(m2)，w(x,t)是梁沿外载荷方向的位移(m)，M(x,t)是弯矩(N·m)，f(x,t)是外部载荷(N).

梁弯矩和应力间的关系为

其中σ(x,t)是应力(Pa).粘弹性材料的变分数阶模型为

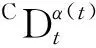
将(12)～(14)式代入(11)式，得到两端固定梁的控制方程为

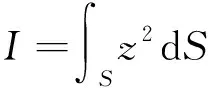
初始条件为

(18)

3 移位Bernstein多项式数值算法

应用移位Bernstein 多项式对梁位移控制方程在时域内进行数值求解，算法结构如图2所示.

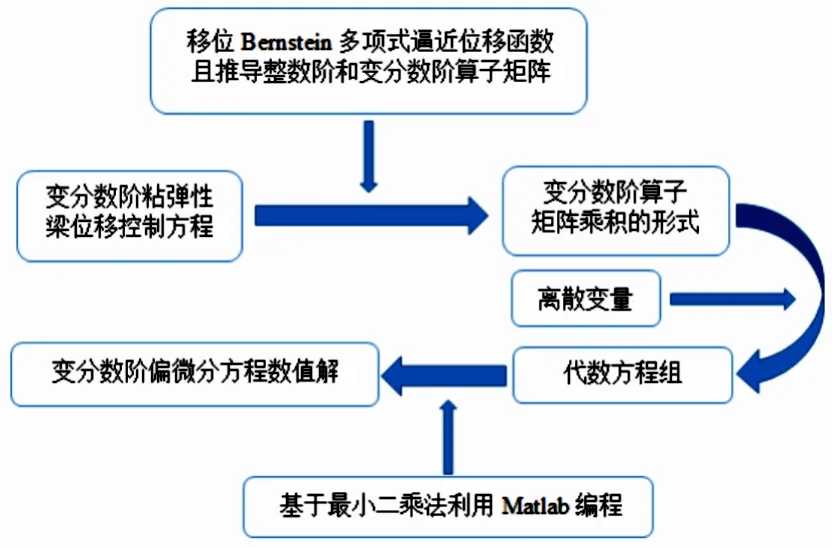
图2 移位Bernstein多项式的数值算法结构

3.1 基函数逼近位移函数

位移函数w(x,t)∈L2([0,L]×[0,R])用移位的Bernstein多项式去逼近，即

其中ui,j为二维函数，U为函数逼近系数.

3.2 整数阶微分算子矩阵

定义4如果存在矩阵D,使得φ′(x)=Dφ(x)，则称D为关于x的一阶微分算子矩阵，即

其中

将(20)式左右两边再求一次导数，有

φ″(x)=D2φ(x).

(23)

根据(20)和(23)式，应用数学归纳法可得

φ(k)(x)=Dkφ(x),

(24)

根据(19)和(23)式可以得到

3.3 变分数阶微分算子矩阵

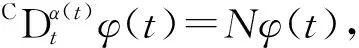
显然，有

其中

结合(19),(24)和(26)式，有

将(25)和(29)式代入(15)式，梁位移控制方程转化成矩阵乘积的形式

边界条件可以重新写为

初始条件可以重新写为

φT(x)Uφ(0)=φT(x)UDφ(0)=0.

(33)

利用配点法，将(30)式的变量进行离散得到一组代数方程组.应用Matlab和最小二乘法求得ui,j，代入原来方程即可得到两端固定梁的位移数值解.

4 数值分析

4.1 变分数阶微分方程数值解的比较

本节求解粘弹性梁位移控制方程算例的数值解，并对精确解与数值解进行比较.控制方程对应的一般算例为

边界条件

初始条件

其中

变分数阶函数α(t)=-0.1t+1,t∈(0,1).数值算例的精确解为w(x,t)=x2(1-x2)t2,x∈(0,1),t∈(0,1).

采用移位Bernstein多项式置配算法时，多项式的项数选择为n=4；用该算法求解变分数阶偏微分方程的算例时，数值解表示为wn(x,t).

图3为一般数值算例的数值解和精确解在x=0.5处的比较.由图可知，数值解和精确解的图像高度一致，说明文中算法对求解变分阶微分方程具有可行性.图4显示的是数值解和精确解的绝对误差e(x,t)=|wn(x,t)-w(x,t)|，绝对误差数量级可以达到10-11，进一步证明本文算法对解决变分数阶粘弹性梁问题具有足够高的准确性.

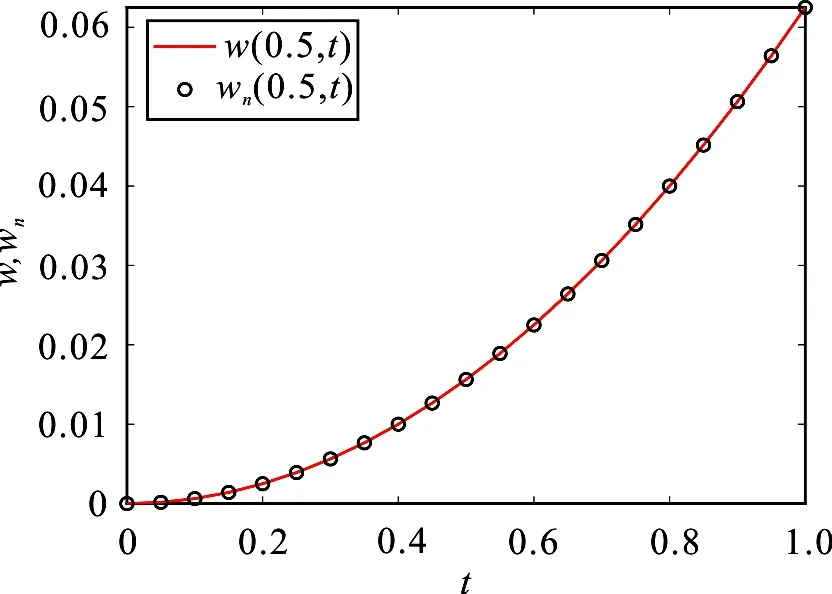
图3 算例的数值解与精确解

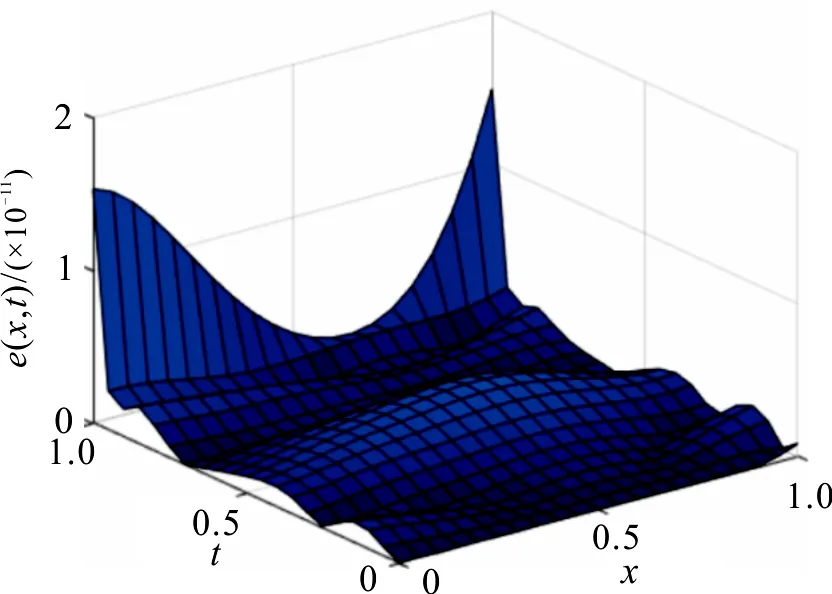
图4 数值解的绝对误差

4.2 不同载荷下的粘弹性梁分析

下面利用本文算法对混凝土梁进行模拟运算，混凝土材料的相关参数如下[20,21]：E=1 000 MPa,θ=0.18 s,ρ=4 000 kg·m-3.选取梁的长度l=5 m,横截面积S=0.01 m2,惯性矩I=0.14/12,变分数阶函数α(t)=-0.1t+1,t∈(0,1).

将数据代入梁的控制方程(15)，利用本文算法对粘弹性梁在不同载荷下进行数值求解.在不同均布载荷作用下，混凝土梁在不同位置和时间的位移数值解如图5所示.粘弹性梁的两端位移始终为零，不受时间的影响，这与边界条件是一致的.在其它位置，粘弹性梁的位移随时间逐渐增大，在t=1 s时达到最大值.粘弹性梁的最大位移在梁中部x=2.5 m处.梁的位移关于中间位置对称.

比较图5(a)和(b)可知，当粘弹性梁上施加的均布载荷不同时，其位移也不同.在f(x,t)=10的均布载荷下，位移最大值约为0.14 m，在f(x,t)=20的均布载荷下，位移最大值为0.29 m，说明粘弹性梁的位移随所施加的均匀载荷的增加而增加，这一结论与文献[22]的结论相一致.与分数阶方程相比，变分数阶方程能够较准确地模拟大应变下粘弹性梁的动态行为,因而具有更广泛的应用.

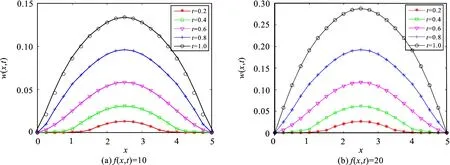
图5 不同均布载荷下的位移数值解

粘弹性梁在线性载荷作用下梁的位移随线性载荷斜率的增加而增大.当斜率为2(图6(a))时，梁的最大位移约为0.09 m；当斜率为4(图6(b))时，梁的最大位移约为0.19 m.

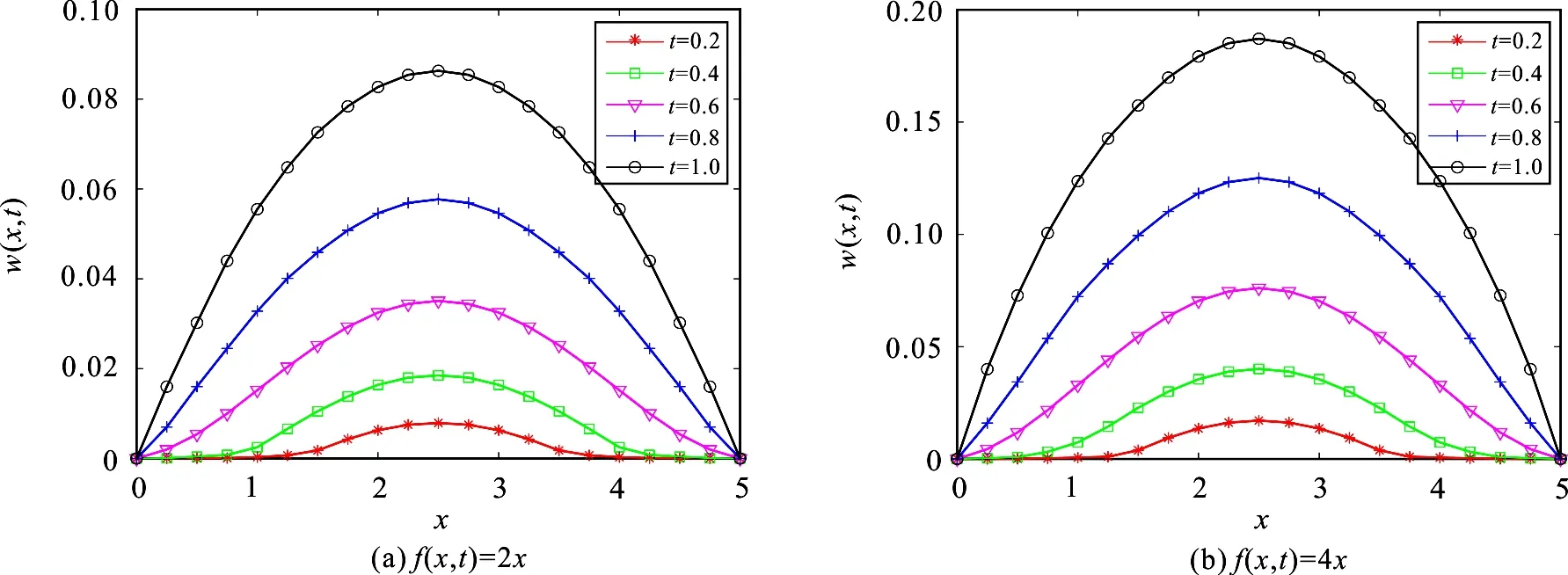
图6 不同线性载荷下的位移数值解

5 结束语

文中基于移位Bernstein多项式对变分数阶粘弹性梁提出了一种有效的数值算法.基于两端固定梁的动力学方程、粘弹性材料变分数阶本构关系和应变位移关系建立了变分数阶粘弹性梁的控制方程，数值分析结果表明，该算法求解变分数阶偏微分方程具有高效性;不同载荷下，混凝土梁的位移随时间的增大而增加,梁的位移在梁中间位置处达到最大值且关于其对称;混凝土梁的位移会随着均布载荷的增加而增加，同时也会随着线性载荷斜率的增加而增大.