基于三维点云的植物叶片重建及其面积估算*

陈 柱，杨 君*

(1.武汉科技大学冶金自动化检测技术教育部工程研究中心，湖北 武汉 430081；2.武汉科技大学信息科学与工程学院，湖北 武汉 430081)

植物叶片大小是监测植物生长及预测植物生长的重要参数之一[1]，也是植物生长管理的重要依据；叶片面积是植物生长发育过程中的一个重要评价指标。 叶片面积测量由最初的回归系数法[2]、方格纸法等发展到基于立体视觉三维点云的建模方法[3-8]。 基于立体视觉的三维点云重建技术为监测植物生长和测算叶片面积提供了新方法。 文献[3]利用Kinect v2 传感器进行三维重建。 文献[4]在机械臂上安装摄像头采集植株图像，采用多视角立体成像(multi-view stero，MVS)算法生成点云。 MVS算法可应用于任何种类或形态的植物，为植物自动化三维重建提供了一种方法，但文献[4]存在图像采集方法复杂的问题。 文献[5]利用3DSOM 软件进行植株三维重建，利用相机、三脚架、旋转平台等设备搭建图像获取系统，最终可获得多角度拍摄的植株图像，但当图像数量较多时，存在重建模型效果较差且设备复杂的问题。 文献[6]概述了运动恢复结构算法和多视角立体算法的原理，同时指出算法重建结果可能会出现孔洞等问题。 文献[7]利用3D 激光扫描仪从多个角度捕获植物的表面点云数据，同时提出用于粗略初始配准的特征点匹配算法并建立了植物的三维模型，使用三角剖分算法计算得到重建网格的表面积和体积。 文献[8]通过CNN网络，从单幅RGB 图像中得到待重建场景的深度图、分割图及平面参数，然后将平面深度图与相机标定获取的相机参数相结合，得到像素点的三维点云深度信息。

与上述方法相比，多视角拍摄二维图像的运动恢复结构(SFM)算法[9]更有优势，因为算法只需用到一台相机且能自动处理相机标志定位问题。 文献[10]采用运动恢复结构算法获取稀疏点云，并把点云分割、表面重建等算法结合，最终得到较精确的叶片面积。 SFM 算法在处理植株这类复杂结构对象时，稀疏点云的三维结构信息不足以完成植物的三维重建。 为解决上述问题，学者们把SFM 算法和MVS 算法结合，从而得到三维信息足够多的稠密点云。

为处理叶片重叠导致叶面积测量不准确的问题，本文提出了一种植物叶片三维重建补偿方法。该方法首先利用相机多角度拍摄植物图像；其次结合SFM 算法、CMVS 算法与PMVS 算法处理图像生成点云数据；然后对点云数据进行去噪、分割、填补、网格化处理；最后计算叶片面积。

1 方法与过程

本研究首先采用运动恢复结构(structure from motion，SFM)算法对多角度拍摄的二维图像进行处理，获得叶片的三维稀疏点云数据，再采用聚类多视角立体(clustering multi-view stereo，CMVS)算法和基于面片的多视角立体(Patch-Based Multi-View Stereo，PMVS)算法处理三维稀疏点云得到三维稠密点云；其次通过颜色特征空间阈值方法去除三维稠密点云的噪点；然后采用K-means++聚类算法对叶片的三维稠密点云进行分割；分割后用Harris 角点检测算法寻找分割重叠叶片的角点，通过角点对缺口叶片进行填补；最后用滚球算法对叶片进行网格化处理并计算叶片面积。 过程如图1 所示，算法分为四个步骤，依次为输入图像、点云重建(SFM 算法，CMVS/PMVS 算法)、稠密点云优化(点云去噪，点云分割，点云填补)、网格化及面积计算。

图1 总体算法流程图

1.1 实验材料

实验材料选取普通的树叶叶片，实验叶片分为四类:①叶片之间无重叠；②叶片小部分与另一叶片重叠；③叶片大部分与另一叶片重叠；④叶片交叉重叠。 本文仅考虑两片叶片重叠的情况。 其中类1 有五片叶片，编号为a1、b1、c1、d1、e1；类2、3、4 均有两片叶片，编号依次为a2、b2、a3、b3、a4、b4。 如图2所示。

图2 叶片重叠情况分类

图3 为多角度拍摄的50 幅类1 叶片图像。 每幅图像尺寸为3 024×3 024，图像为JPG 格式。 四种类别叶片各采集50 幅图像。

图3 50 幅类1 叶片图像

1.2 点云重建

点云重建由稀疏点云重建与稠密点云重建两个步骤组成。

1.2.1 稀疏点云重建

SFM 算法处理二维图像形成三维稀疏点云。图4 为SFM 算法流程。

图4 SFM 算法流程图

首先输入图像，采用尺度不变特征转换(Scale invariant feature transform，SIFT)算法[11-12]对二维图像进行特征提取与特征匹配；其次通过几何验证筛选图像匹配对完成图像配准；然后从图像匹配对特征点的像素坐标开始，利用对极几何原理，计算得到基础矩阵；在基础矩阵奇异分解运算后再进行三角化运算，得到特征点在世界坐标系下的坐标；最后使用光束法平差(Bundle adjustment，BA)最小化重投影误差。

重投影误差为真实三维空间点在图像平面上的投影与重投影的差值。 重投影误差图如图5 所示，轨迹j上的3D 点Xj投影至相机i的2D 图像平面上形成的点I(Ci，Xj)，即为三维空间点在图像平面上的投影点；虚拟三维空间点qij为重投影点。

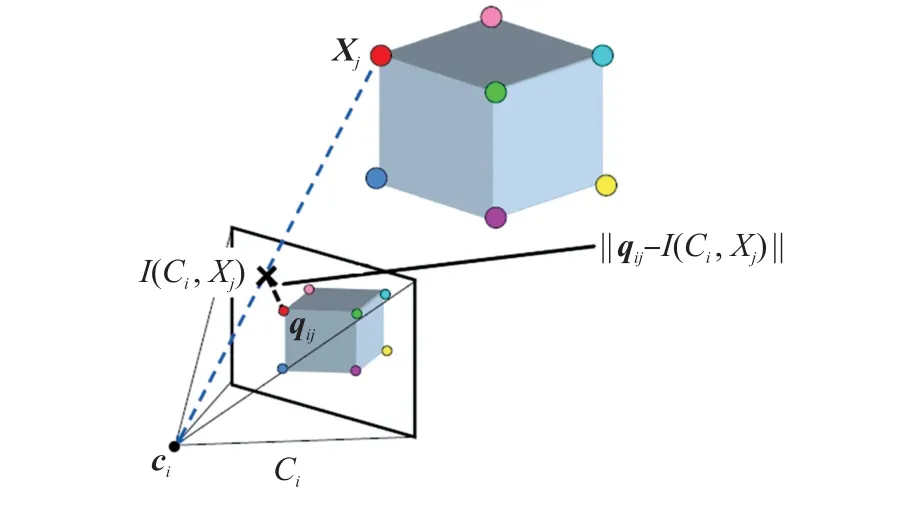
图5 投影误差图

当存在m个轨迹与n个拍摄视角时，重投影误差累计和g(C，X)为式(1):

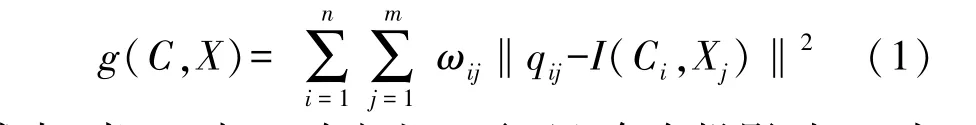
式中:当3D 点Xj在相机i平面上存在投影时，ωij为1，反之为0。 通过迭代的方式使累积和逐渐收敛到最小值，最终得到最优的相机姿态与稀疏点云。

1.2.2 稠密点云重建

稠密点云由稀疏点云获得法向量并向外扩散形成。 稠密点云重建分为两步:

①在紧密性、图像大小、覆盖范围的约束下，CMVS 算法将稀疏点云聚类到不同的图像簇。

②在局部光度一致性、全局可视化一致性的约束下，PMVS 算法将稀疏点云匹配、扩展、过滤[13]得到稠密点云。

本文通过VisualSFM 软件和MeshLab 软件实现SFM 算法和CMVS/PMVS 算法。

图6 为三类重叠叶片的稀疏点云重建结果、稠密点云重建结果和拍摄叶片时相机的空间位置。 图6 左半部分为稀疏点云重建结果，对三类叶片图像进行稀疏点云重建后，分别得到15 567、14 832、17 963 个 特 征 点， 生 成1 738 455、1 584 126、1 984 136个稀疏点。 图6 右半部分为稠密点云重建结果，生成的稠密点云较稀疏点云能更好的还原叶片真实形态。

图6 稀疏点云结果(左)与稠密点云结果(右)

1.3 点云去噪

在重建过程中，叶片存在白色背景或叶片表面反光导致叶片边缘存在噪点，如图6 叶片点云边缘所示。 本研究以点云颜色与噪点颜色存在差异为依据滤除噪声。

本文采用MATLAB Color Threshold 工具箱提取点云的HSV 颜色特征阈值[10]，归一化后三个通道的阈值范围依次为[0，0.225]、[0.395，0.969]、[0.067，0.585]，然后利用阈值范围生成掩膜矩阵。

我们先将点云数据的颜色矩阵作为初始对象生成新的颜色矩阵，以掩膜矩阵为索引生成所有点新的坐标矩阵；后将新的颜色矩阵和新的坐标矩阵写为点云格式，生成去噪后的叶片稠密点云。 去噪结果如图7 所示，图7 与图6 对比，去噪后叶片稠密点云边缘噪声点显著减少。 三类叶片点云数剩余1 553 845、1 321 255、1 626 512 个。

图7 叶片点云去噪结果

1.4 点云分割及填补

本文采用无监督聚类K-means++算法[14]来实现点云分割，对三类重叠叶片点云聚类分割的结果如图8 所示，完整叶片点云为深色，缺口叶片点云为浅色。

图8 三类重叠叶片分割图

类1 叶片能正常分割，不用填补，其他重叠叶片均需填补。

填补缺口叶片需找到缺口叶片点云的角点。 角点是连接物体轮廓线的点，它可以展现图像的图形特征并帮助减少运算量。 本文采用Harris 角点检测算法[15]寻找待填补叶片点云的角点。 Harris 角点检测算法选取某像素的领域窗口，当窗口在各个方向上滑动且窗口内像素平均灰度值产生较大变化时，则认为选取的像素点为角点。

以类2 叶片为例，填补算法步骤为:

①采用Harris 角点检测算法找到类2b2叶片点云处于缺口边缘的角点e21、e22，连接e21、e22形成线段l2，如图9(a)所示；

②移动线段l2至同一枝叶的另一完整叶片点云a2上，线段l2构成的平面将完整叶片点云截取为两部分s21、s22，规定s21为大面积，s22为小面积，如图9(b)、图9(c)所示；

③根据缺口叶片待填补大小选择s21或s22填补至缺口叶片点云b2，如图9(d)所示，选择s22；

④若填补后仍有空洞，则采用漫水填充算法[16]填充孔洞，填补算法完成，如图9(e)所示。

由图9(e)可看出填补算法对类2b2叶片进行了有效填补，使b2叶片的空缺部分得到填补。 类3、类4 叶片同理，如图10、图11 所示。

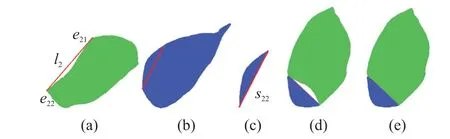
图9 类2 b2 叶片点云填补图

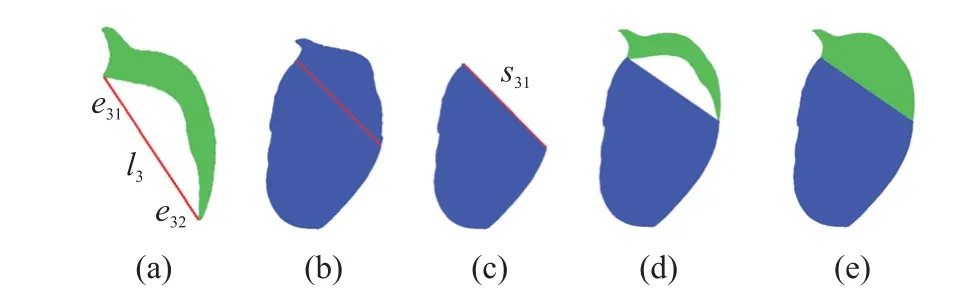
图10 类3 b3 叶片点云填补图

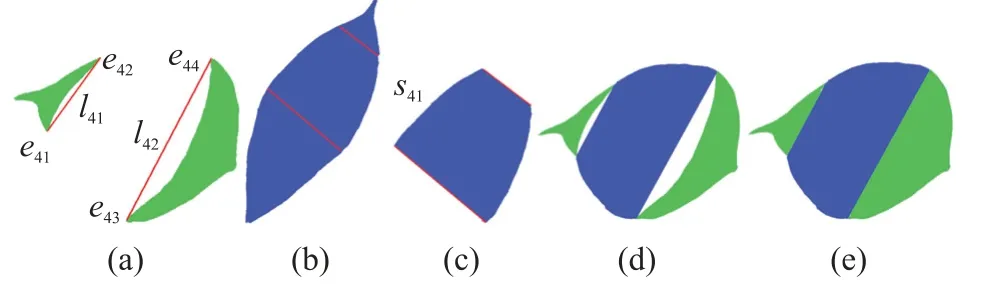
图11 类4 b4 叶片点云填补图

1.5 网格化及面积计算

1.5.1 网格化

本文采用滚球算法对稠密点云进行三角网格化，使用自适应半径的方法使球在搜索过程中更容易遇到新的点，可避免仅使用单一半径进行数据点搜索而留下孔洞。

滚球算法步骤为:首先，在点云中随机选取一点，寻找与其距离最近的两个点并将三点连接形成三角形；其次，将三角形的三条边作为网格的边界并列为备选边，选择三角形的一条边作为轴，使用自适应半径的方法使轴旋转生成球；然后，球在点云表面滚动且接触到新的点时，将该点和上述备选边连接形成新三角形并列入重建网格，将新形成的边列为备选边，同时将上一步生成的边取消备选；最后，再从备选边中选择下一边重复上述操作，直至所有点都参与滚动并生成三维三角网格。

类1a1叶片通过滚球算法得到的三维三角网格如图12 所示，叶片三角网格与真实叶片接近。

1.5.2 面积计算

本文在网格化后对所有三角网格面积求和，叶片面积是上述所有三角网格面积的累加。

以网格中△BCD 为例，如图13 所示，根据△BCD 三点的坐标可确定各边边长为:

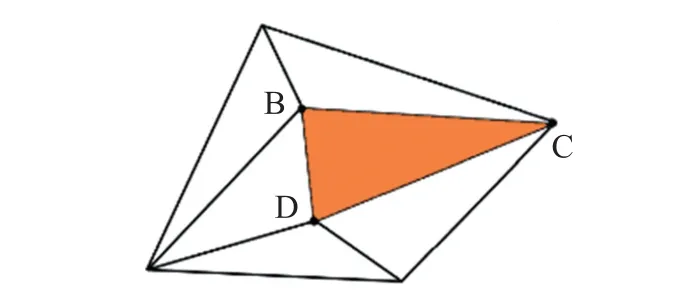
图13 BCD 三角网格图

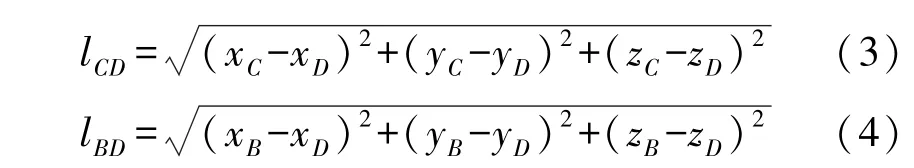
式中:lBC、lBD、lCD为△BCD 的三条边长，(xB，yB，zB)、(xC，yC，zC)、(xD，yD，zD)分别为点B、C、D 的坐标。

根据海伦凯勒公式可得△BCD 的面积为:

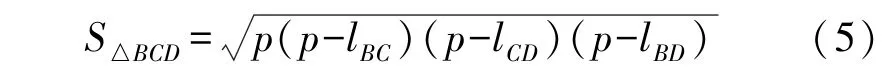
式中:S△BCD为△BCD的面积，p为半周长，值为(lBC+lCD+lBD)/2。

按上述方法可求得网格中所有三角形的面积，最后累加所有三角形的面积可得近似的叶片面积，累加公式如式(6):

式中:S叶为叶片面积，SΔ为单个三角网格的面积，t为三角网格序号，n为网格总数。

2 结果与分析

以扫描法为标准，将本文方法与方格纸法进行对比。 扫描法测量叶片面积时，将单个叶片按压平放至扫描仪1 ∶1 扫描。 对扫描的图像进行灰度处理，统计叶片像素数占纸张像素数的比例，已知纸张面积，通过比例计算得到叶面积。 方格纸法选取方格面积为0.25 cm2方格纸。 统计单个叶片占方格纸的数量，将满格和大于半格计为0.25 cm2，小于半格计为0 cm2。 图14、图15 依次为方格纸法和扫描法处理类1a1叶片得到的结果。

图14 类1 a1 叶片方格纸法结果

图15 类1 a1 叶片扫描法结果

扫描法的精度接近真实值，故本文把扫描法的结果作为对比标准。

方格纸、扫描法和本文方法计算所有编号叶片的面积，结果如表1。

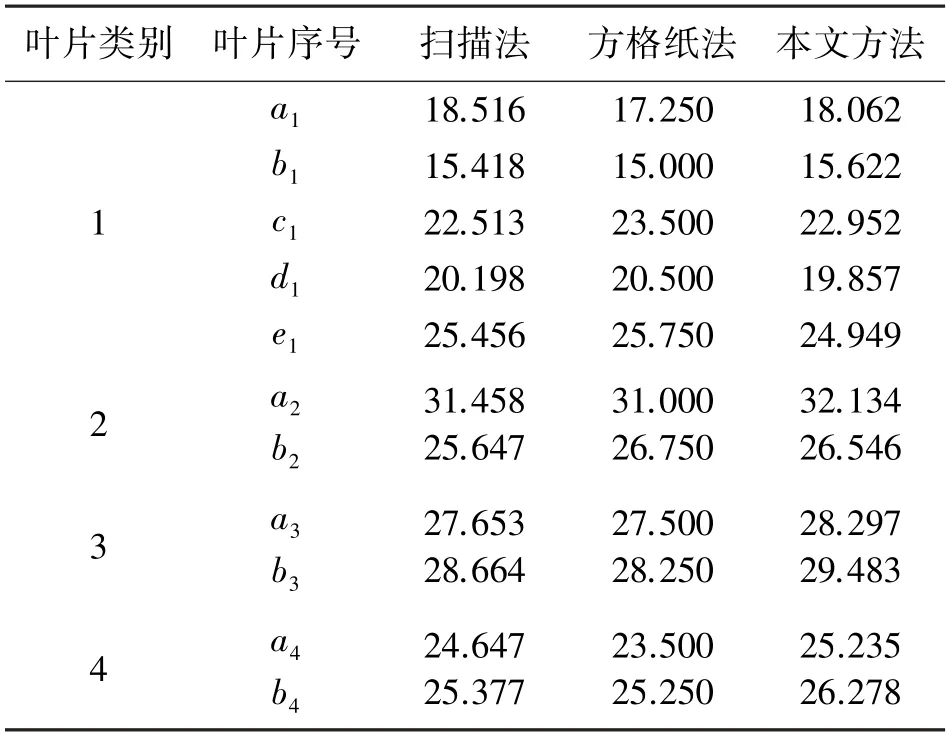
表1 叶面积计算结果 单位:cm2

由表1 数据可看出，本文方法相对于方格纸法更接近精度较高的扫描法。

表2 第三列是对重叠叶片的面积，第四列是对重叠叶片填补的面积。

表2 本文方法填补前后叶面积 单位:cm2

由表2 数据可知，三类重叠的b 叶片在填补处理后面积增加了3.810 cm2、27.337 cm2、18.116 cm2。填补后的结果更接近扫描法，验证了填补处理的有效性。

3 结论

本研究采用三维点云重建的方法测算叶片面积，对重叠叶片进行填补来处理面积测量不准确的问题。 填补处理能有效解决由于重叠导致的叶面积测量不准确的问题，与方格纸法相比，本文方法更接近扫描法，并有效地还原真实叶片面积。