一类扰动七次哈密顿系统的极限环
张景涛,余秋里,洪晓春
(云南财经大学 统计与数学学院,云南 昆明 650221)
1 引言和主要结论
俄国数学家V.I.Arnold在1977年提出了弱化的希尔伯特第16问题, 即研究扰动哈密顿系统的阿贝尔积分孤立零点个数的上界,这个上界也就是扰动哈密顿系统的极限环个数的上界. 文献[1]研究了系统
(1)
在任意n次多项式扰动下的阿贝尔积分孤立零点个数的上界问题, 得出上界为3[(n-1)/4]+ 12[(n-3)/4]+22(n≥5), 这个上界也是系统(1)在任意n次多项式扰动下极限环个数的上界. 由于扰动的Liénard系统

(2)
可以模拟电台和真空管道的震动,从而受到了学者们的广泛关注, 这里0<|ε|≪1,Rm(x)和Rn(x)分别是关于x的多项式, 而且deg(Rm(x))=m, deg(Rn(x))=n.
文献[2]研究了系统

(3)
并证明了系统(3)的阿贝尔积分最多有2个零点.
对于扰动的五次哈密顿系统
(4)
当p(x,y)=a0+a1x2+a2y2时, 文献[3]得出系统(4)可以同时出现3个极限环,还给出了出现双尖点极限环的情况. 当p(x,y)=a0+a1x2+a2y2+a3x2y2时, 文献[4]得出系统(4)可以同时出现4个极限环,也给出了出现双尖点极限环的情况.
对于扰动的五次哈密顿系统

(5)
其中p(x)=a0+a1x+a2x2+a3x3,文献[5]得出系统(5)可以同时出现4个极限环,4个极限环具有2种分布情况.
对于七次扰动系统
(6)
其中0<ε≪1,ai(i=0,1,2,3)∈R,p(x)=a0+a1x2+a2x4+a3x6. 文献[6]从理论上证明了系统(6)的阿贝尔积分在区间(0,1/24)上最多有4个零点,对于一些特殊的ai也可以有3个零点, 该文给出了系统(6)的极限环个数的上界. 因此,受文献[1-6]的启发,我们通过定性理论分析,借助于数值计算对其判定函数[7]进行研究,分析系统(6)的极限环分支情况,得出系统(6)可以同时出现3个极限环,最后使用数值模拟方法[8]对得出的结果进行了检验,并且给出了这些极限环的具体位置.
2 对未扰动系统的定性分析
为了研究扰动系统(6), 现在先分析未扰动系统
(7)
系统(7)是一个哈密顿系统,其首次积分为
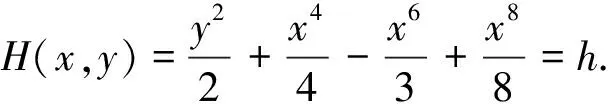
(8)
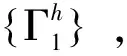
3x8-8x6+6x4-24h=0.
(9)

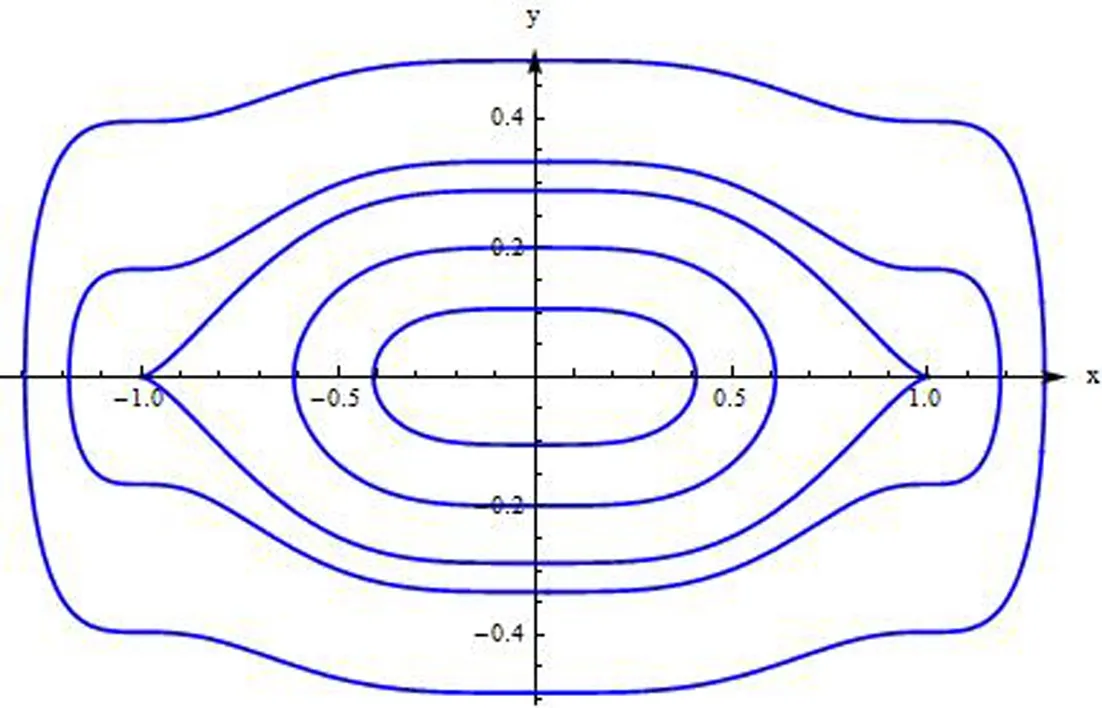
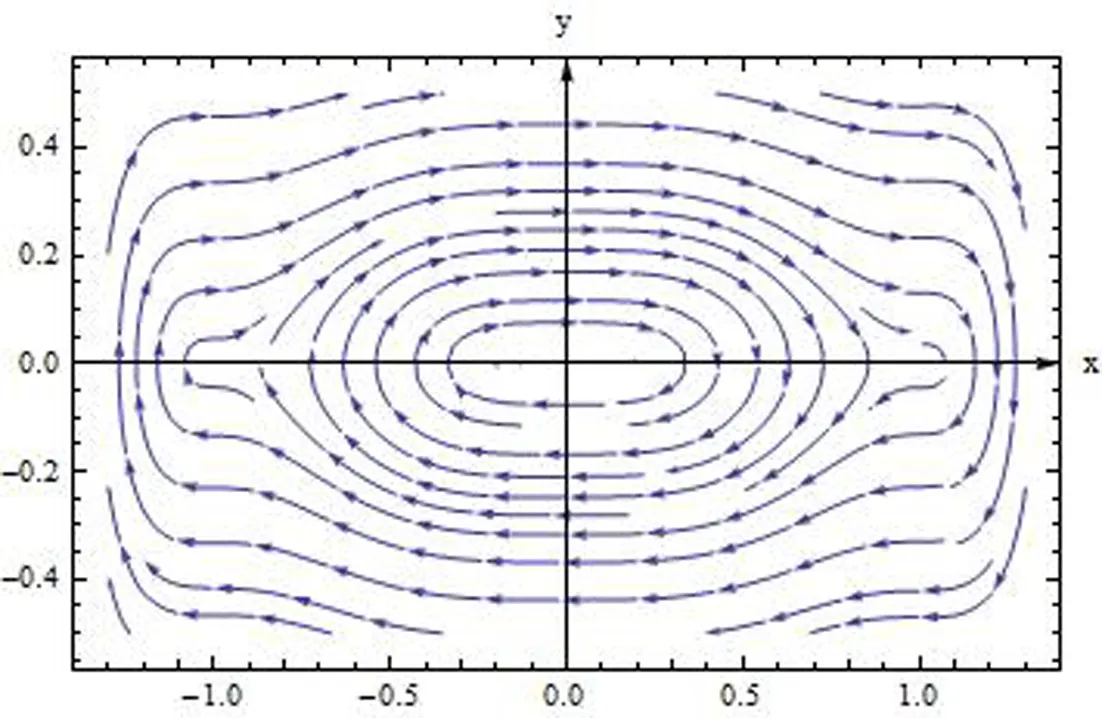
图1 系统(7)的相图和向量场图
3 扰动系统的判定函数与极限环
现在考虑扰动系统(6), 由文献[9]中的(3.1.4),我们可得其阿贝尔积分为
A(h)=∮Γh(a0+a1x2+a2x4+a3x6)ydx
=∬Γh(D)(a0+a1x2+a2x4+a3x6)dxdy,
(10)
其中Γh(D)为闭轨线Γh所围的内部区域. 令A(h)=0, 可得

(11)
由(11), 可得两个判定函数如下:

(12)

∞),
(13)
当a1=-0.8,a2=5.8,a3=-7.5时,由(12)、(13)及(9), 我们使用数值计算方法得系统(6)的判定函数表1, 又由表1得判定函数对应的函数曲线(称为判断曲线)图2, 其中红色曲线段部分是函数(12)对应的曲线, 绿色曲线段是函数(13)对应曲线的一部分.

表1 当a1=-0.8, a2=5.8, a3=-7.5时, 系统(6)的判定函数
使用文献[7]中定理1的办法,由系统(6)的判定曲线图2,可以得到以下结论:

图2 当a1=-0.8, a2=5.8, a3=-7.5时, 系统(6)的判定曲线
定理1 对于系统(6), 当a1=-0.8,a2=5.8,a3=-7.5,而且
(i)a0(h)=-0.0151203或a0(h)>0.016578时,系统出现1个极限环.
(ii)-0.0151203 (iii)0 当ε=0.001,a1=-0.8,a2=5.8,a3=-7.5时,分别特取a0=0.004,a0=0.00825727,a0=0.013,使用数值模拟方法[8],我们给出系统(6)中同时出现的3个极限环的具体位置(见图3-5). 在图3中,大、中、小极限环顺次经过点(0.9549,0)、(0.6006,0)、(0.1386,0), 它们依次是稳定的、不稳定的、稳定的; 在图4中,大、中、小极限环顺次经过点(1,0)(双尖点极限环)、(0.5682,0)、(0.2137,0), 它们依次是稳定的、不稳定的、稳定的; 在图5中,大、中、小极限环顺次经过点(1.027,0)、(0.5125,0)、(0.3048,0), 它们依次是稳定的、不稳定的、稳定的. 图3 当a0=0.004, a1=-0.8, a2=5.8, a3=-7.5, ε=0.001时, 系统(6)同时出现的3个极限环的分布情况 图4 当a0=0.00825727, a1=-0.8, a2=5.8, a3=-7.5, ε=0.001时, 系统(6)同时出现的3个极限环的分布情况 图5 当a0=0.013, a1=-0.8, a2=5.8, a3=-7.5, ε=0.001时, 系统(6)同时出现的3个极限环的分布情况 我们应用判定函数方法[7]和数值模拟方法[8]研究了系统(6)的极限环分支情况. 结果表明,系统(6)可以同时分支出3个极限环,且内外极限环都是稳定的,中间的是不稳定的, 或者内外极限环都是不稳定的,中间的是稳定的. 本文未能找到系统(6)同时出现4个极限环的具体情况, 我们的结果只能说明系统(6)可以同时分支出3个极限环, 不一定可以同时分支出4个极限环, 因为我们知道,对于任何系统而言, 系统的极限环个数≤系统的阿贝尔积分孤立零点的个数. 以上内容为纯理论研究, 研究系统的极限环个数及分布情况, 对于许多实际问题,若系统能够出现一个稳定极限环, 这是一种非常好的性态,例如在生物数学中, 研究人员也研究这一类极限环问题, 见文献[10-12]等.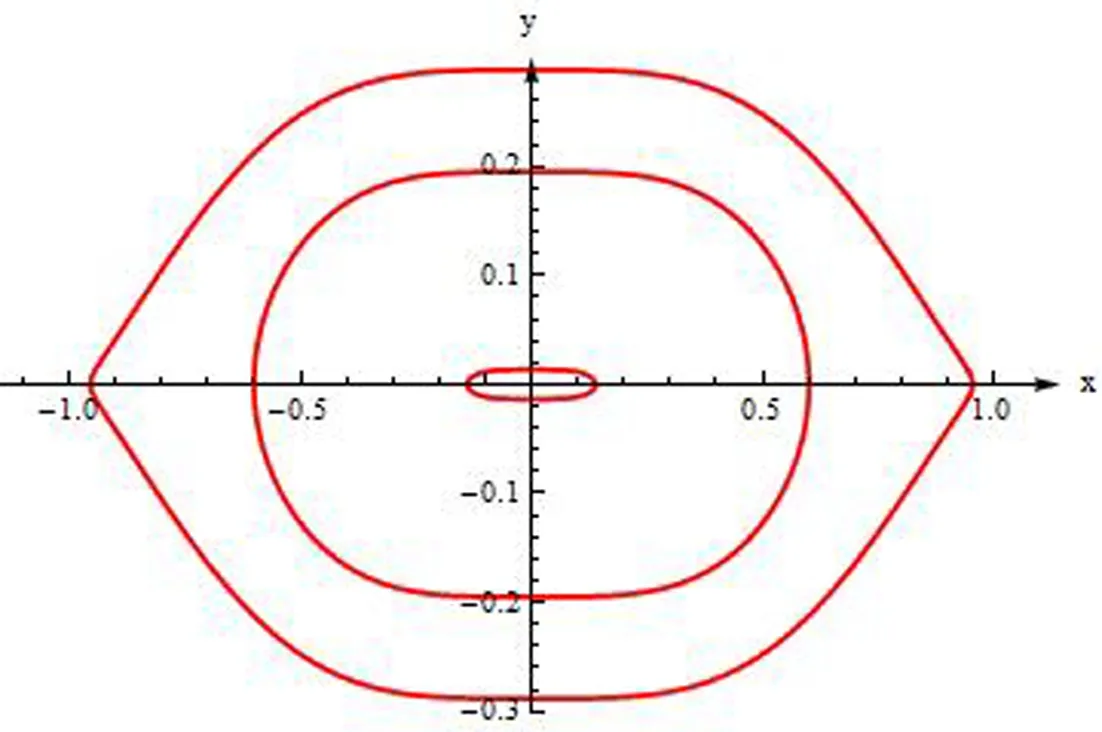

4 结 论

