基于RSM和BP-GA的甲基橙脱色条件的优化

高大响，黄小忠，陈智豪

（江苏农林职业技术学院，江苏句容 212400）

甲基橙是一种结构较复杂的偶氮类有机物，稳定性强，不易被降解，作为着色剂在纺织、造纸、印染以及食品工业方面应用广泛。目前甲基橙染料废水的处理方法主要有超声法［1-2］、电化学法［3-4］、光催化法［5-6］、芬顿氧化法［7-8］、自由基氧化法［9］等。这些方法存在技术复杂、设备投入大、运行费用高等问题，在实际应用中均存在一定的条件限制。因此，找到一种廉价、实用的降解方法，具有相当重要的现实意义。

大豆富含高活性的脂氧合酶［10］，加工豆制品产生的废水中也含有一定的活性脂氧合酶［11-12］。脂氧合酶催化不饱和脂肪酸氧化产生的初期产物脂质氢过氧化物和自由基等生理活性物质的化学性质活泼，可以起到氧化剂的作用［13］，进而直接与蛋白质、核酸反应［14］，还能氧化降解类胡萝卜素、叶绿素等［15］。有效利用脂质氢过氧化物和自由基等活性成分，在改变面筋结构、面条加工以及面粉漂白等方面有很多应用［16-18］，而在污染防治以及废水治理等环保领域的研究报道不多［19］。

RSM 是利用合理的实验设计和数据，采用多元二次回归方程拟合因素与响应值之间的函数关系，通过回归分析来寻求优化工艺参数。BP 神经网络是人工神经网络（ANN）的一种，也是近几年来快速发展起来的人工智能技术之一。GA 是借鉴生物界自然选择和群体进化机制形成的一种全局寻优算法，通过GA 对BP 神经网络进行全局寻优，可以获得优化方案［19］。本实验利用制备豆浆产生的黄浆水，在前期甲基橙脱色率的研究基础上［20］，以甲基橙完全脱色时间为目标，考察温度、pH 及甲基橙初始质量浓度对脱色时间的影响。分别利用响应面分析法（RSM）和BP 神经网络对脱色过程进行建模，采用插值算法对散点实验数据进行曲线拟合，利用GA 对BP 神经网络训练模型进行寻优，以获得最短脱色时间。

1 实验

1.1 材料与仪器

材料：大豆（市售），甲基橙。

仪器：九阳豆浆机、生化培养箱（江苏天翎仪器有限公司），723 型可见分光光度计（上海菁华科技仪器有限公司）。

1.2 黄浆水的制备［19］

将大豆在水中浸泡14～24 h，取出浸泡好的大豆加入豆浆机中打浆［m（大豆）∶m（水）=1∶6］；过滤豆渣，进一步煮沸豆浆并保持5 min；豆浆冷却至85 ℃，加入无水硫酸钙4%（对干豆质量）进行絮凝，静置10 min，过滤收集黄浆水。

1.3 实验方法

1.3.1 甲基橙脱色实验

取敞口静置24 h 的黄浆水，采用双层纱布滤除沉淀并适当稀释，调节pH。取50 mL 稀释液加入100 mL三角瓶中，再加入甲基橙，用黄浆水配制不同初始质量浓度的甲基橙溶液，混匀后置于恒温培养箱，在一定温度下进行脱色反应并开始计时，在不同时间段测试469 nm 处的吸光度直至数值稳定，计算甲基橙完全脱色的时间。

1.3.2 单因素实验

取敞口静置24 h 的黄浆水50 mL，以甲基橙完全脱色时间为因变量，分别改变温度、pH 以及甲基橙初始质量浓度3 个因素，考察其对甲基橙脱色时间的影响；利用插值函数interp 1，同时采用3 次样条插值（spline）法进行插值拟合，并利用Matlab 2015b 编写程序绘制图形。

1.3.3 Box-Behnken 实验

在单因素实验的基础上采用Box-Behnken 进行设计，考虑吸光度测定问题，甲基橙初始质量浓度为5～10 mg/L。选取3 因素3 水平设置相应编码值（见表1）。实验点共17 个，包括12 个析因点和用于估计实验误差的5个重复零点。每组实验重复3次，共51次。

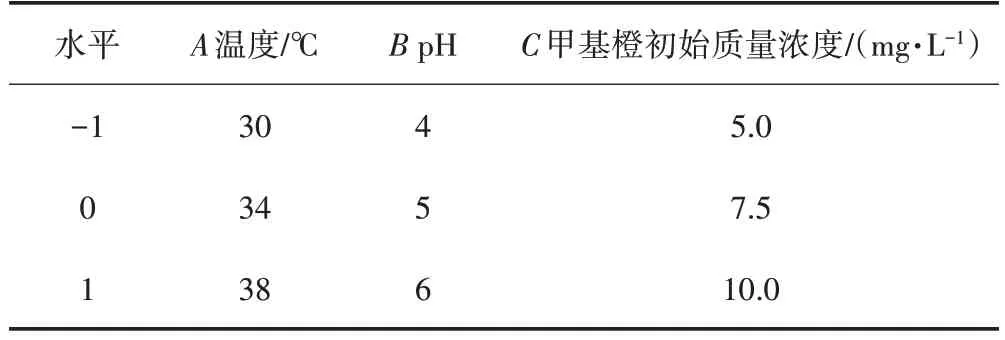
表1 Box-Behnken 实验因素与水平

1.4 优化模型

1.4.1 响应面模型

基于Box-Behnken 的实验数据均值进行响应面建模，得到如下公式：

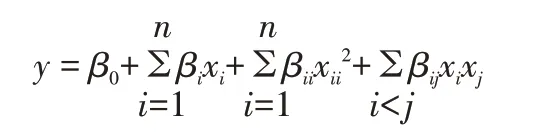
式中：y表示方程响应值（脱色时间，min）；β0是常数；βi、βii、βij分别为一次项系数、二次项系数和交互项系数；xi和xj为自变量编码值。Box-Behnken 实验结果的方差及回归分析在Design-Expert8.06软件中进行。

1.4.2 BP 神经网络模型

选取温度、pH、甲基橙初始质量浓度作为输入变量，甲基橙完全脱色时间为输出变量，输入变量范围见表1。以Box-Behnken 实验和BP 模型补充实验的81 个实验结果作为原始样本数据导入Matlab 2015b，采用3 层BP 神经网络进行建模，并编写相应程序。在训练前将实验数据随机分为69 个训练样本和12 个检验样本（预测样本）。分别检验在1～20 个隐层节点数情况下，预测结果与实际结果的误差绝对值之和，由此确定隐层节点数。再对样本进行建模，输入层传递函数为tansig，输出层传递函数为purelin，训练函数为traingda，学习率Ir 为0.05，最大训练步数为1 000，均方误差（MSE）目标设为1×10-5。为了提高学习能力，在训练前将实验数据进行归一化处理。

1.5 插值算法曲线拟合

用Matlab 2015b 对实验的样本数据进行编程，实现网格节点数据的插值和曲线拟合，三维网格生成使用meshgrid 函数，插值函数采用griddata。

1.6 基于BP 模型的GA 寻优

在Matlab 2015b 中输入命令optimtool，打开优化工具箱，求解器选择Genetic Algorithm，变量数选择3，以训练好的BP 模型作为适应度函数编写M 文件。变量上下限分别为［30 4 5］和［38 5 10］，GA 其他参数分别为：初始种群20，交叉概率0.90，变异概率0.05，进化代数100，其他保持默认。

2 结果与讨论

2.1 甲基橙脱色时间的影响因素

由图1 可以看出，pH、温度以及甲基橙初始质量浓度对黄浆水中的甲基橙脱色时间有明显影响，在其他因素不变的情况下，当pH 为5，温度约为35 ℃时，脱色时间最短，甲基橙脱色时间随着甲基橙初始质量浓度的升高而逐渐延长。

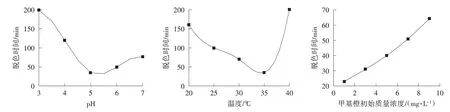
图1 pH、温度、甲基橙初始质量浓度对脱色时间的影响

2.2 响应面

Box-Behnken 实验设计及多元回归拟合结果见表2，方差分析结果见表3。

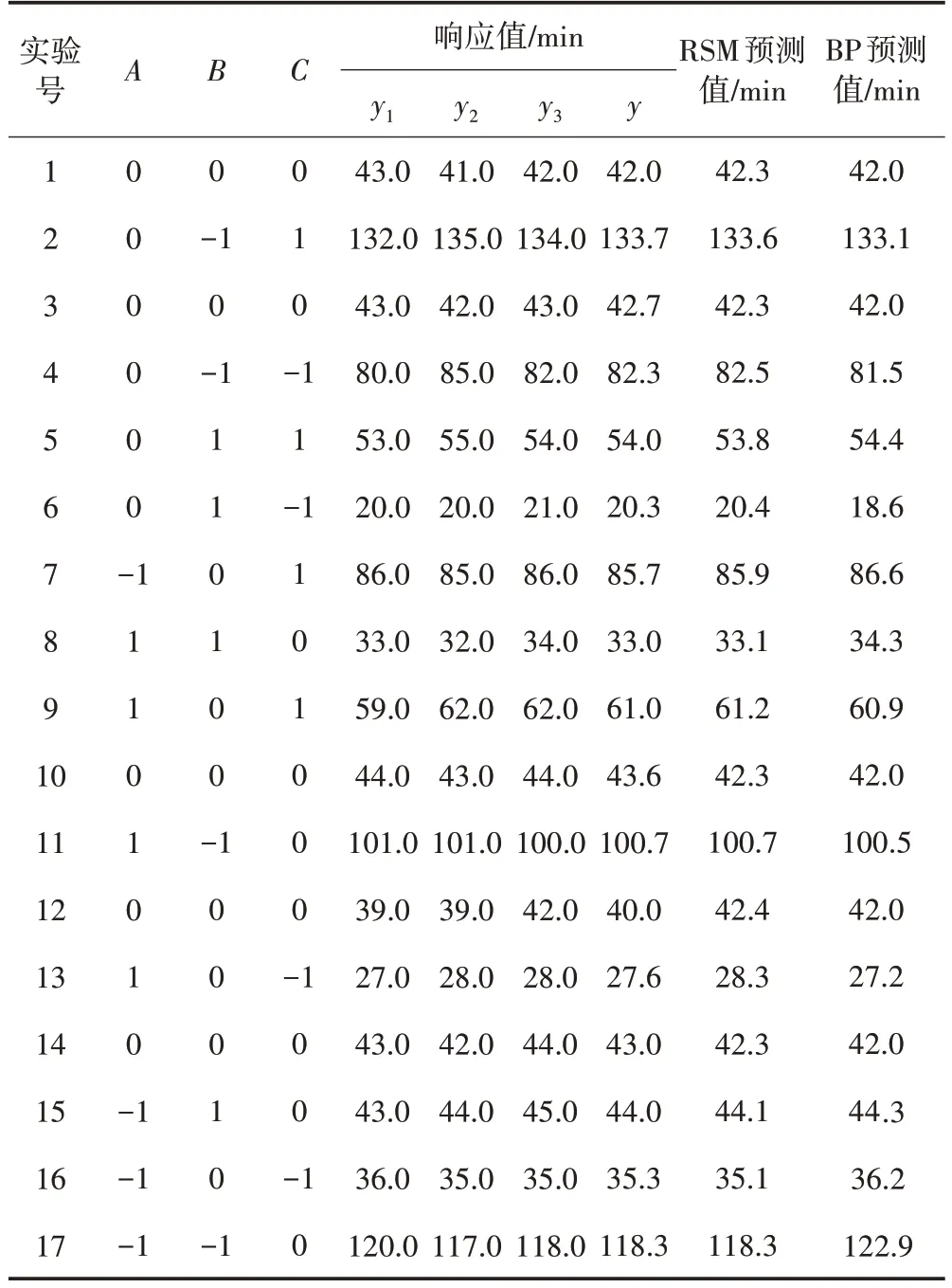
表2 Box-Behnken 实验设计及多元回归拟合

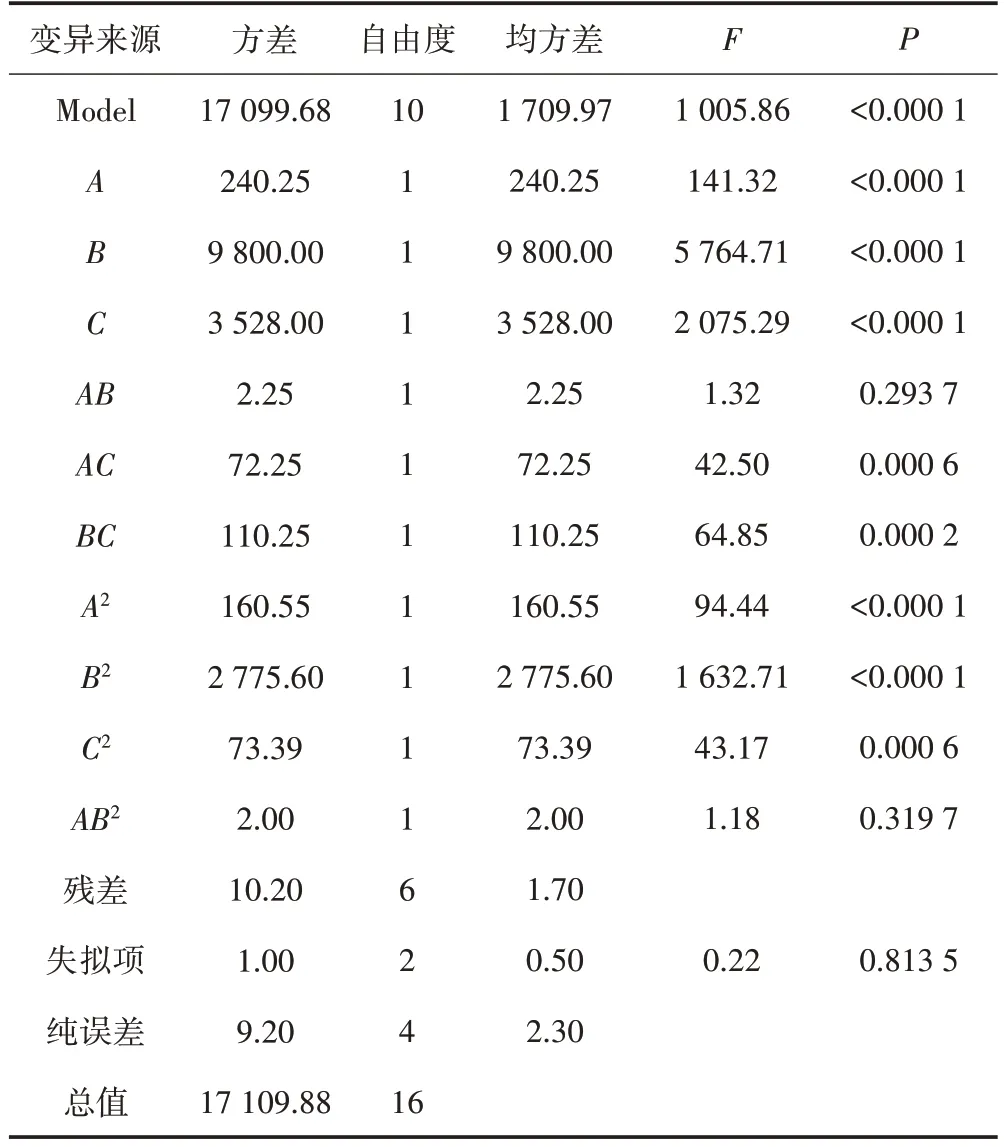
表3 方差分析

由表3 可知，回归模型P<0.000 1，表明模型能较好地描述甲基橙的脱色过程，实验方法可靠。模型失拟项P=0.813 5>0.050 0，差异不显著，说明模型预测值与实验值拟合的概率较大，拟合良好，回归方程的失拟平方和基本由实验误差等偶然因素引起；同时，该模型回归复相关系数R2=0.975 3，说明回归方程能够用于表2 中实验数据的拟合。该模型预测优化脱色条件为：温度34.9 ℃、pH 5.6、甲基橙初始质量浓度5 mg/L、黄浆水中甲基橙脱色的最短时间16.7 min。

方差分析结果表明，A、B、C3 因素以及二次项对甲基橙的脱色时间均有极显著的影响（P<0.01），交互项AC、BC也有极显著的影响，而AB的影响不显著。响应面分析得到脱色时间对温度、pH 和甲基橙初始质量浓度的二次多项式回归模型为：y=978.118 75-19.681 25A-197.375 00B+23.330 00C-2.312 50AB-0.425 00AC-2.100 00BC+0.385 94A2+17.175 00B2+0.668 00C2+0.250 00AB2。

2.3 BP 神经网络建模补充实验

由于BP 神经网络建模需要足够的实验数据才能保证模型的准确，在RSM 实验数据基础上，另补充10组共30个实验数据（见表4）。

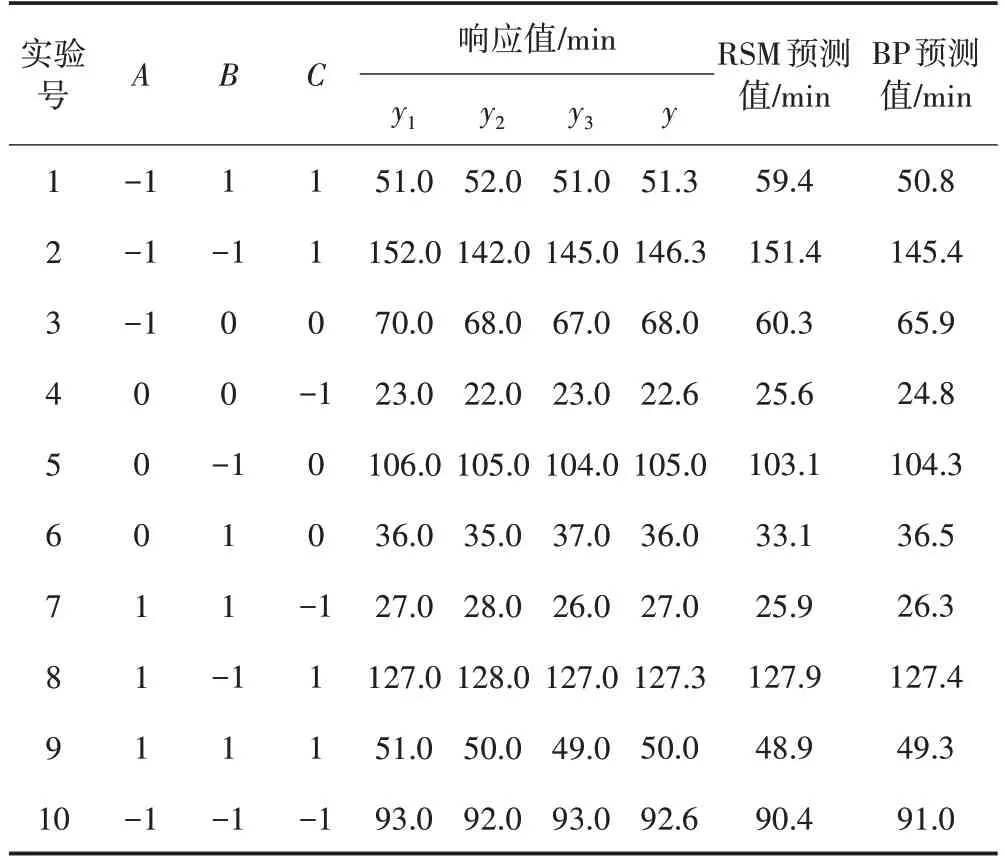
表4 补充脱色实验和RSM、BP 模型预测

2.4 BP 神经网络的建立与检验

BP 神经网络建模以表2 和表4 中的A、B、C为输入值，各自对应的实验值为输出值，将81 组实验结果用于BP 模型的建立。为获得更好的网络性能，依次选择1～20 个隐层节点数，以训练均方误差大小为指标，训练后得到相应的误差平方和，结果如图2所示。

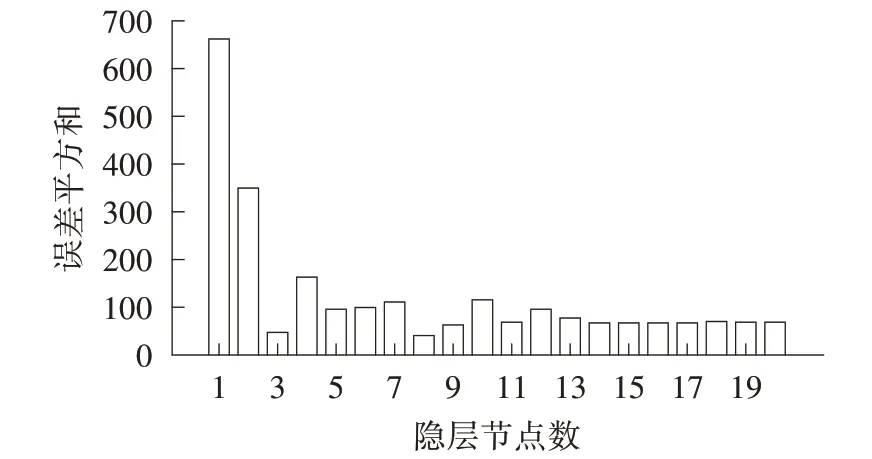
图2 不同隐层节点数下对应的误差平方和

由图2 可知，当隐层节点数为8 时，误差平方和最小，最后确定BP 神经网络的拓扑结构为3-8-1。选择8 个隐层节点数对BP 神经网络进行训练，经过481次迭代后，网络收敛精度达到10-3，网络停止训练，训练曲线如图3所示。

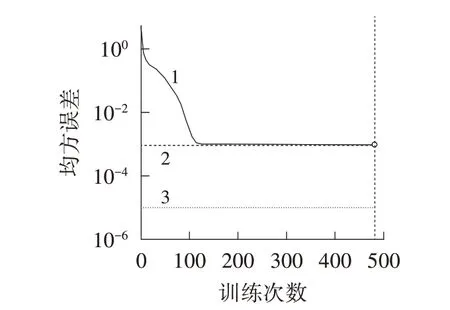
图3 BP 神经网络训练过程

由图4 可以看出，训练模型随机产生的12 个预测结果与实验值的拟合度较好，两者间的预测误差（如图5 所示）在5%（绝对值）以内，说明建立的BP 神经网络性能良好。

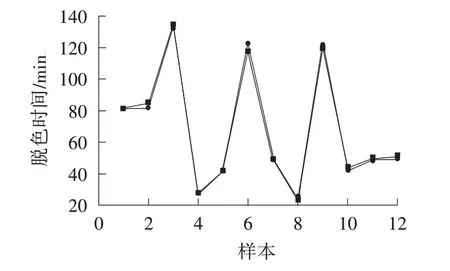
图4 检验样本预测脱色时间和实际脱色时间

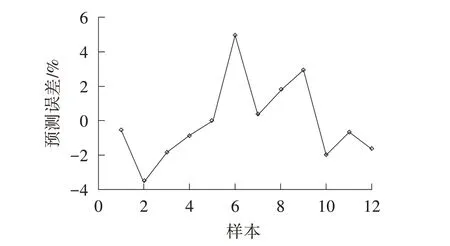
图5 BP 神经网络预测误差

2.5 插值算法拟合曲线和遗传算法优化

以表2、表4 的实验数据在Matlab 2015b 平台上编写程序代码，采用四维制图技术和插值算法拟合温度、pH、甲基橙初始质量浓度与甲基橙脱色时间的关系。由图6 可以看出，温度、pH 和甲基橙初始质量浓度间存在明显的交互关系。当黄浆水中的甲基橙质量浓度为5 mg/L，温度接近34.4 ℃，pH 为5.5 时，脱色时间最短。通过对实验散点数据进行插值分析和曲线拟合，便于实现编程，光滑度好，能较好地反映数据变化的规律，预测优化［21-23］。

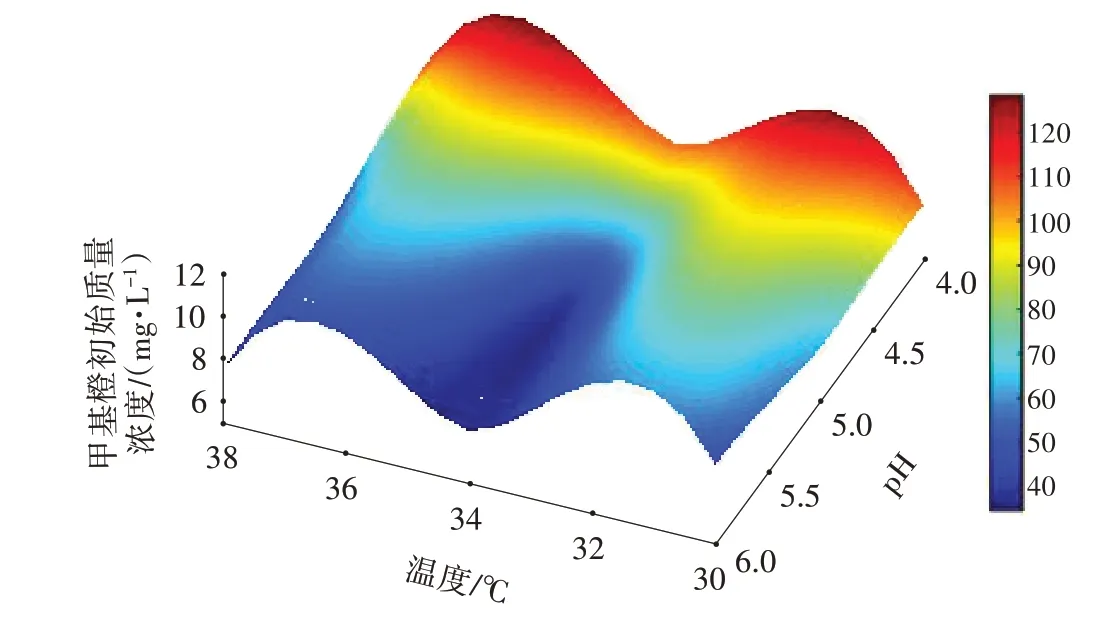
图6 插值算法拟合曲面图

在训练好的BP 神经网络模型的基础上，利用GA对脱色条件进行全局寻优。经过迭代43 次后，适度函数值趋于稳定，GA 找到了模型的最小值（如图7、图8所示）。当温度为34.4 ℃、pH 为5.5、甲基橙初始质量浓度为5 mg/L 时，脱色时间预测值为15.7 min。因此，当把BP 模型与遗传算法相结合，可以快速得到优化变量。基于BP 模型的GA 寻优与通过插值算法预测的脱色条件基本一致。

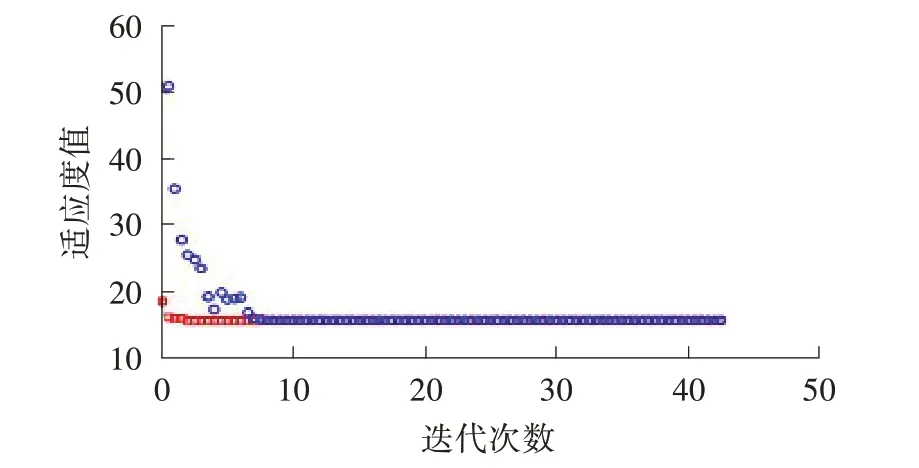
图7 GA 中适应度值变化过程

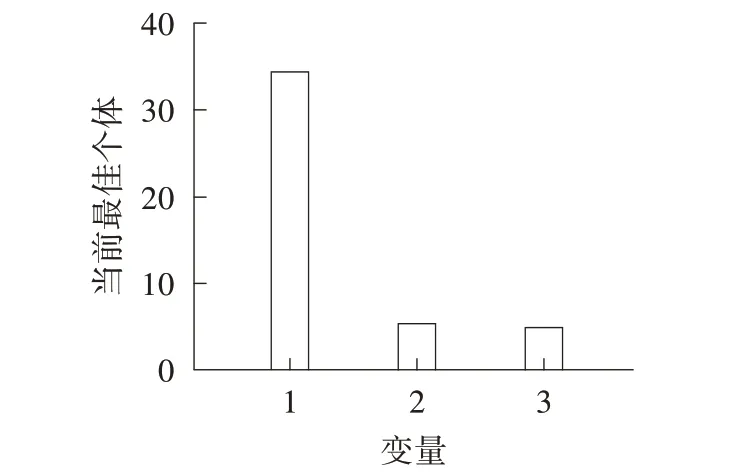
图8 GA 优化的最佳个体

当黄浆水中甲基橙质量浓度为5～10 mg/L 时，根据优化的脱色工艺条件进行实验，在温度为34.4 ℃、pH 为5.5、甲基橙初始质量浓度为5 mg/L 时，甲基橙脱色时间为16 min，与GA 寻优的结果一致。

2.6 脱色时间比较

对比10 组实验数据，以RSM 回归方程计算甲基橙脱色时间、BP 模型输出预测脱色时间，并分别与实验均值进行比较，结果如表4 和图9 所示。RSM 回归模型和BP 训练模型均能很好地预测不同条件下的甲基橙脱色时间，相比RSM 回归预测，BP 训练模型对数据的预测值更接近实验观察值，说明BP 模型的拟合效果比RSM 模型更好。

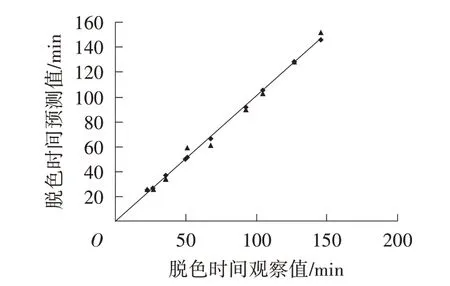
图9 BP 模型和RSM 模型预测的脱色时间与实验值对比

3 结论

（1）响应面分析法及其构建的回归方程能够对实验数据进行拟合和预测。预测的甲基橙优化脱色条件：温度为34.9 ℃、pH 为5.6、甲基橙初始质量浓度为5 mg/L，此时黄浆水中的甲基橙脱色时间最短为16.7 min。

（2）在补充数据的基础上，利用拓扑结构3-8-1的BP 神经网络对甲基橙脱色过程进行训练，并利用GA寻优，实验验证获得甲基橙脱色时间的优化条件：温度34.4 ℃、pH 5.5、甲基橙初始质量浓度5 mg/L，此时黄浆水中甲基橙的脱色时间最短约16 min。

（3）在数据较充足的情况下，BP 模型相比RSM模型具有更好的预测能力和外推能力。这可能是由于RSM 建立的数学回归模型属于二次多项式，对于给定的有限数据拟合能力有限；而BP 模型不需要预先给定函数，在实验数据足够的基础上，经过反复训练可以获得一个反映实验数据内在联系的数学模型，具有极强的非线性处理能力。