基于干扰观测器的平面2RR并联机器人高速运动的滑模控制
董楸煌, 陈志伟
(1.福建农林大学机电工程学院;2.现代农业装备福建省高校工程研究中心;3.福建省农业信息感知技术重点实验室,福建 福州 350002)
并联机器人具有刚度大、精度高、响应速度快等优点,针对不同的实际应用需求,有不同机构形式的并联机器人,其应用领域越来越广.随着机器人和机器视觉等技术的发展和交叉融合,在自动化生产线上利用机器人进行快速的动态分拣操作,并拓展到自动化、智能化农业生产装备等领域.例如可利用DELTA并联机器人或SCARA机器人进行快速分拣[1-4].DELTA并联机器人虽然具有较高的运动速度,但是并联机构的运动链闭链约束较多,使得其工作空间范围相对较小,不适合末端执行器在大范围工作空间运动[5].SCARA机器人的驱动电机和减速装置多安装于每个关节位置,这必然造成机器人的运动惯性较大,高速运动状态下会对系统产生较大的冲击.在自动化分拣操作时,大范围平面工作空间内的高速动态分拣操作,以及利用DELTA或SCARA等典型的机器人都存在不足之处.平面五连杆并联机器人的驱动装置均安装在基座,采用轻质运动连杆可有效减小运动惯性,具有较大的工作空间和较少的自由度,且可采用混合驱动方式,以节省硬件成本[6-7].
目前,关于并联机器人的研究主要集中在并联机器人机构学、运动学规划、动力学与控制等问题[8-10].赵匀[11]利用机构数值分析,对平面五连杆机构各杆件的长度等几何参数的设计要求进行分析.马承文等[6]采用杆件长度设计和质量分配方法对五连杆机构的动力学进行解耦合.上述研究并没有涉及动力学控制问题,而实际机器人的工程应用操作控制,需要结合动力学与控制等基础理论,才能达到理想的运动控制效果.韩江等[12]基于U-K方法对3RR并联机器人闭链约束关系进行动力学建模,并设计鲁棒伺服约束控制方法实现对末端轨迹的跟踪控制.张青云等[9]对刚柔耦合空间并联机器人提出一种前馈补偿的PD控制方法,实现轨迹跟踪与振动抑制.并联机器人机构运动链存在封闭几何约束关系,使得并联机器人的动力学模型存在高度非线性、强耦合的复杂关系[13].
本研究对一种平面2RR并联机器人进行动力学分析,针对机器人快速分拣操作要求,以及系统动力学方程存在的非线性、强耦合和不确定外界干扰等因素,设计了一种基于干扰观测器的滑模控制方法,以实现运动控制;通过李雅普诺夫稳定性判定,证明了该控制方法的可行性;并通过数值仿真试验,进一步分析该控制方法的效果.
1 动力学分析
应用于快速分拣的平面2RR并联机器人如图1所示.其末端执行器的工作空间结构特征为平面,结合机器视觉识别技术,可对不同颜色、大小和形状等特征有差异的目标载荷进行快速分拣,比如自动生产线上的工业产品,以及类球形果蔬、平面木质板材等非结构特征明显的农林产品,可有效提高分拣操作的工作效率和稳定性.
平面2RR并联机器人是五连杆组成的封闭运动链平面机构,可以看成是由两个平面二连杆机械臂子系统组成的.两个子系统的一端通过旋转关节与基座连接,另一端通过旋转关节连接在一起,形成并联机器人的末端执行器(图2).与基座相连的关节A1和A2由电机提供驱动力矩,为并联机器人系统的主动关节,中间关节B1和B2为无动力驱动的被动关节,E关节安装末端执行器,将驱动电机安装于基座上,可有效减小并联机器人结构的运动惯性,减小高速运动对动载荷的影响.
以主动关节A1为坐标原点,建立惯性参考坐标系o-xy,同时以各关节为坐标原点,建立各连杆的随体坐标系oi-xiyi(i=1,2,…,4),机器人的各个连杆相对于惯性参考坐标系x轴线的转动角度为θi(i=1,2,…,4).并联机器人系统的自由度为2,选取主动关节旋转角度θ1和θ4为系统的广义坐标,可利用第二类拉格朗日方程建立系统的动力学方程.
首先,定义拉格朗日函数为:
L=K-P
(1)
式中,K为系统的动能,P为系统的势能.
假设各连杆的质心位于其几何中心,则根据几何关系,可得各连杆质心相对于惯性参考坐标系o-xy的位置坐标为:
(2)
式中,xci、yci(i=1,2,…,4)为各连杆质心相对于惯性坐标系的坐标值,l0为主动关节A1与A2之间的距离,li(i=1,2,…,4)为各连杆的长度.由式(2)对时间求导,可得各连杆质心速度为:
(3)
由式(3)可得整个并联机器人的总动能为:
(4)
式中,mi(i=1,2,…,4)为各连杆的质量,Ii(i=1,2,…,4)为各连杆绕经过质心垂直转轴的转动惯量.
由于并联机器人做平面运动,总重力势能为恒定值,选取运动平面为零势能面(不失一般性),可得系统的总重力势能为零,即式(1)中P=0.
并联机器人系统是一封闭运动链系统,根据闭链几何约束关系可得,末端执行器的位置坐标满足如下约束关系:
(5)
显然,被动关节θ2、θ3均是θ1和θ4的函数,即θ2=θ2(θ1,θ4),θ3=θ3(θ1,θ4),则由式(5)对θ1和θ4求偏导,可推导得[11]:
(6)
可根据式(6)求得主动关节角速度和被动关节角速度之间的映射关系.
根据第二类拉格朗日方程,联立式(4)和式(6),并选取广义坐标θ1和θ4,建立如下平面2RR并联机器人系统的动力学方程:
(7)
式中,L为式(1)中系统的拉格朗日函数,τ1、τ4分别为对应主动关节A1、A2的驱动力矩,即系统的广义力.联立式(1)、式(3)、式(4)和式(6),并代入式(7)中,可推导得到并联机器人系统的动力学方程,并写为矩阵形式:
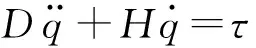
(8)
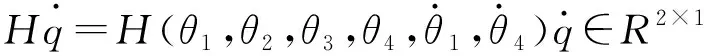
2 控制系统设计
平面2RR并联机器人在分拣操作过程中的高速运动会产生较大的动载荷,分拣的目标载荷也不确定,系统自身的非线性摩擦、外部的不确定扰动和强耦合等特点,使得机器人分拣操作控制系统的设计的难度加大.针对并联机器人上述特点,本文提出基于干扰观测器的平面2RR并联机器人滑模控制方法.滑模控制是一种非线性控制方法,具有较强的抗参数摄动与抗干扰性能,鲁棒性较强,无需精确的系统动力学模型即可对系统进行精确的轨迹跟踪控制.同时,滑模控制方法计算量小、实时性强,适用于对高速运动的控制.在滑模控制方法的基础上,通过引入干扰观测器补偿项,可对系统不确定性和外界干扰进行实时估计,提高控制系统的性能[14-15].
假设将平面2RR并联机器人系统动力学方程的不确定干扰项映射到系统广义坐标上的力矩为fi,结合式(8),系统的动力方程可改写为:
(9)
2.1 滑模控制方法设计
首先,设计控制方法的滑模面为:
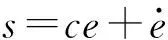
(10)
式中,c为二阶的正对角阵,e=qd-q为广义坐标的状态误差,qd为广义坐标的期望值.
针对机器人系统的动力学方程(式(9)),设计滑模控制方法:
(11)
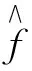
将式(11)代入式(9),可得:
(12)
假设惯量矩阵D-1存在,将式(12)等号两边同时乘以D-1,得到:
(13)
式中,f=-D-1fi.结合式(10)和式(13),可推导得到:
(14)
定义Lyapunov函数为:
(15)
对式(15)求导可得:
(16)
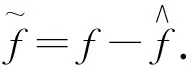
2.2 干扰观测器补偿项设计
为了对不确定干扰项进行辨识,提高控制系统的性能,设计干扰观测器为:
(17)
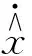
2.3 控制方法稳定性分析
定义Lyapunov函数为:
(18)
对V2求导数,可得:
(19)
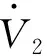
(20)
则结合式(16)和式(20)可得:V<0.
通过设计干扰观测器对不确定干扰项进行实时辨识估计,可使滑模控制切换增溢矩阵取较小的值,以减小并联机器人系统高速运动过程的抖振,提高系统运动控制的稳定性.
3 数值仿真分析
为了验证所设计的控制方法对快速运动并联机器人快速运动的控制效果,以图1中快速分拣并联机器人为例,并通过MATLAB数值仿真分析软件进行仿真验证.
3.1 系统参数和初始条件
快速分拣并联机器人为一做高速运动的平面2RR并联机器人,该机器人的结构原理如图2所示,机器人各连杆的惯性参数、几何参数和初始条件等系统参数如表1所示.
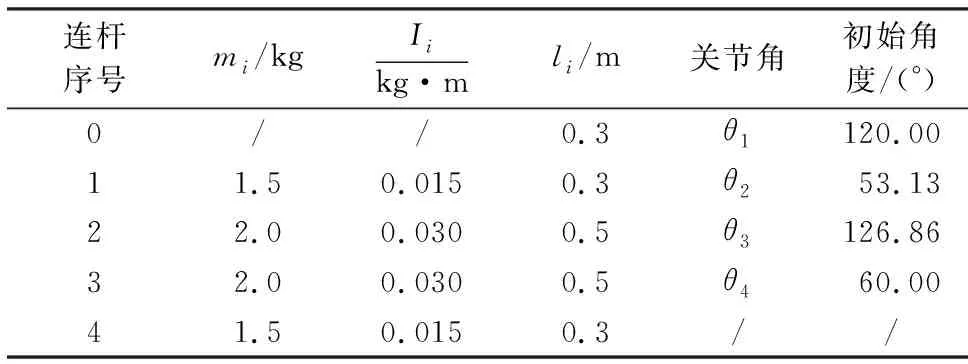
表1 系统参数Table 1 Parameters of the sorting system
3.2 仿真试验分析
3.2.1 连续轨迹的跟踪控制仿真 为了分析所设计的控制方法对于平面2RR并联机器人快速运动控制的效果,将所设计的滑模控制方法与机器人常用的独立PD控制方法进行仿真对比分析.采用PD控制方法使主动关节角度跟踪上期望轨迹,需耗时3 s左右(图3);而采用所设计的滑模控制方法,仅需耗时2 s左右,但是会存在抖振问题(图4).在滑模控制方法基础上,开启干扰观测器,能有效抑制滑模控制方法产生的抖振问题(图5).
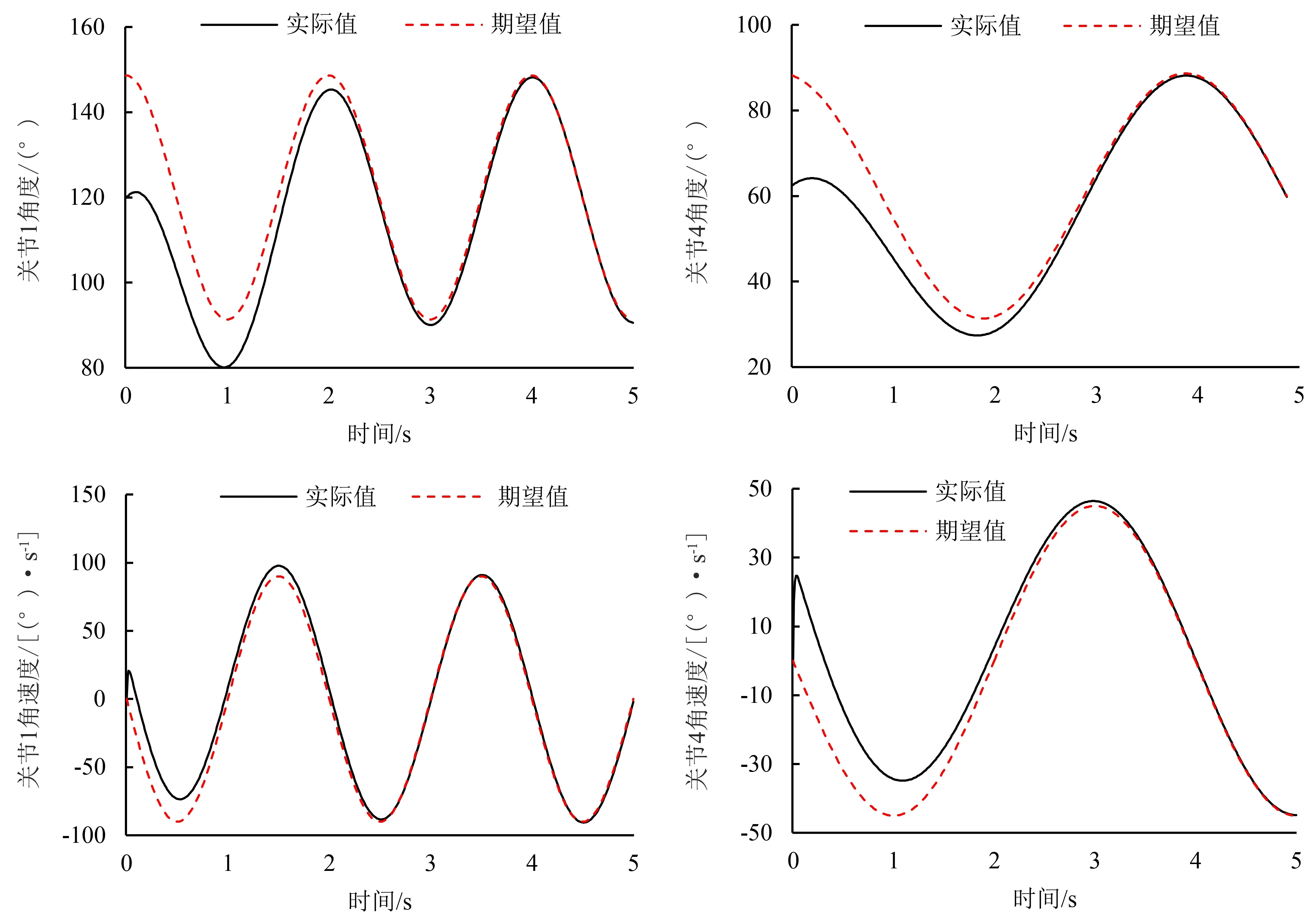
图3 PD控制时主动关节轨迹跟踪效果Fig.3 Tracking performance of active joint trajectory under PD control
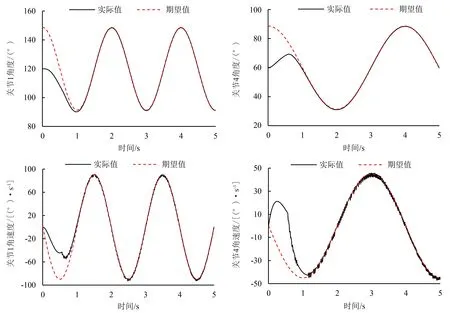
图4 滑模控制时主动关节轨迹跟踪效果(干扰观测器关)Fig.4 Tracking performance of active joint trajectory under sliding mode control (disturbance observer off)
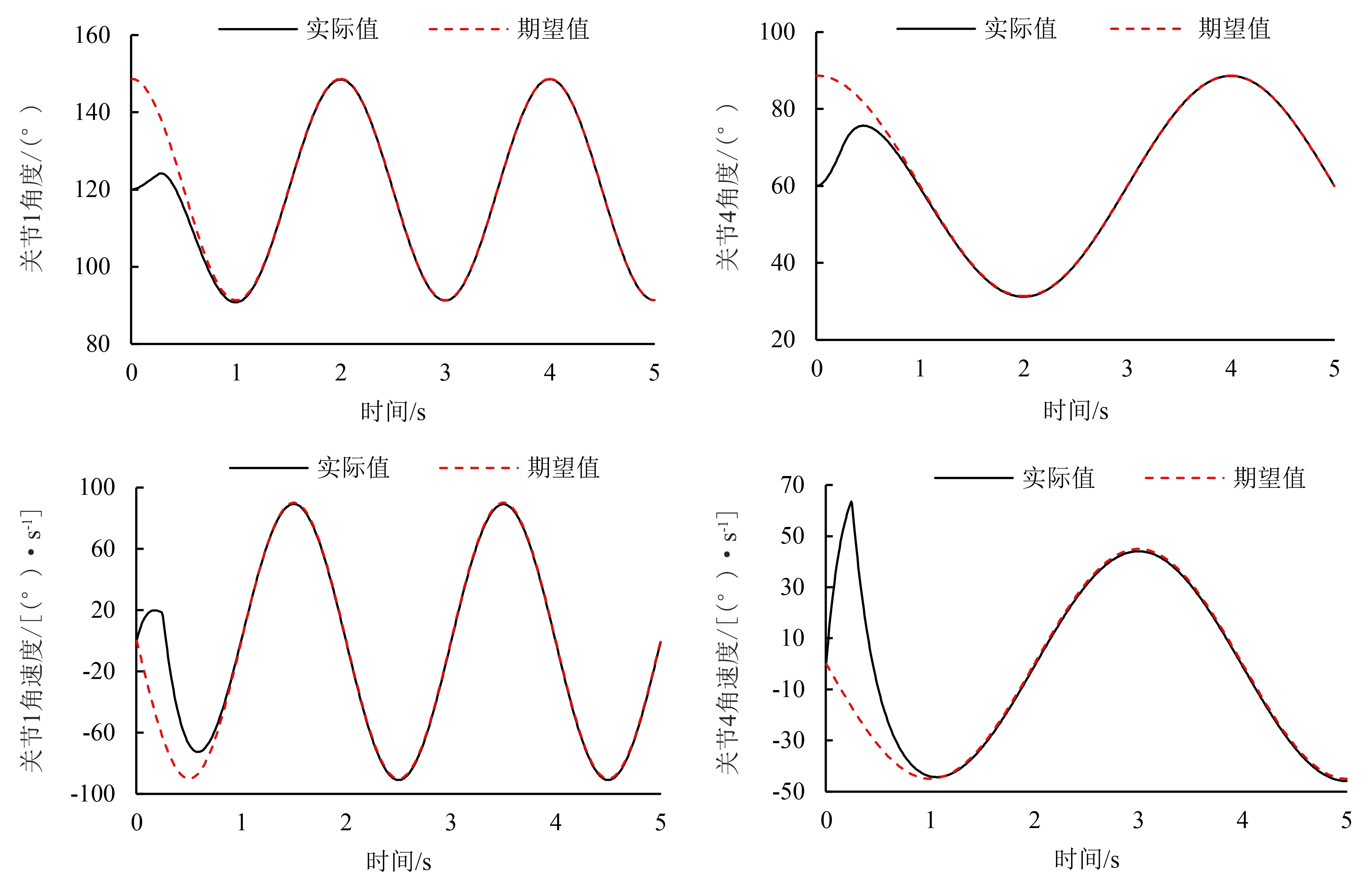
图5 滑模控制时主动关节轨迹跟踪效果(干扰观测器开)Fig.5 Tracking performance of active joint trajectory under sliding mode control (disturbance observer on)
3.2.2 点到点的快速运动控制仿真 并联机器人在进行快速分拣操作时,主要是对末端执行器进行点到点的跟踪控制.在开始时刻,机器人末端执行器在起始点处于静止状态,当末端执行器目标点的期望状态指令输入后,机器人系统开始快速运动到目标点对应的期望构型.仿真时,设置末端执行器目标点对应的主动关节θ1和θ4的期望值为:
θ1d=60°,θ4d=-60°
机器人到达目标点时,对应的期望速度和加速度均为零,被动关节θ2和θ3将在封闭运动链约束下,发生相应的状态变化.控制系统输入采用所设计的基于状态观测器的滑模控制方法,控制系统可调的参数值为:
c=diag[5 5],kf=diag[10 10],k1=diag[0.01 0.01],k2=diag[0.01 0.01]
当干扰观测器关闭,并联机器人系统只在所设计的滑模控制规律作用下进行控制,机器人末端执行器从起始点运动到目标点,对应的主动关节角度和角速度的变化规律如图6所示.在控制器的作用下,系统的关节角度能快速到达期望的构型,对应的关节角速度则存在抖振,无法消除不确定滑模控制方法自身的缺点和不确定干扰的影响,高速运动的并联机器人稳定性较差.
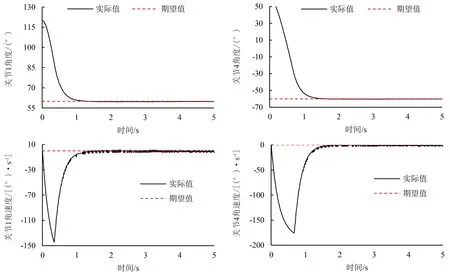
图6 干扰观测器关闭时主动关节状态变化Fig.6 Dynamics of active joint state with disturbance observer off
当干扰观测器开启,并联机器人系统在增加干扰观测器的滑模控制下,对应的关节角度和角速度的变化规律如图7所示.在滑模和干扰观测器共同作用下,系统主动关节角度和角速度都能快速到达期望值状态,有效克服了高速运动并联机器人系统的抖振问题,提高了控制的稳定性.

图7 干扰观测器开启时主动关节状态变化Fig.7 Dynamics of active joint state with disturbance observer on
在控制过程中,平面2RR并联机器人的构型变化过程如图8所示.仿真试验表明并联机器人能从初始构型运动到期望构型,并且系统始终保持封闭运动链的构型状态,这也验证了所建立的动力学方程和闭链几何约束条件的正确性.
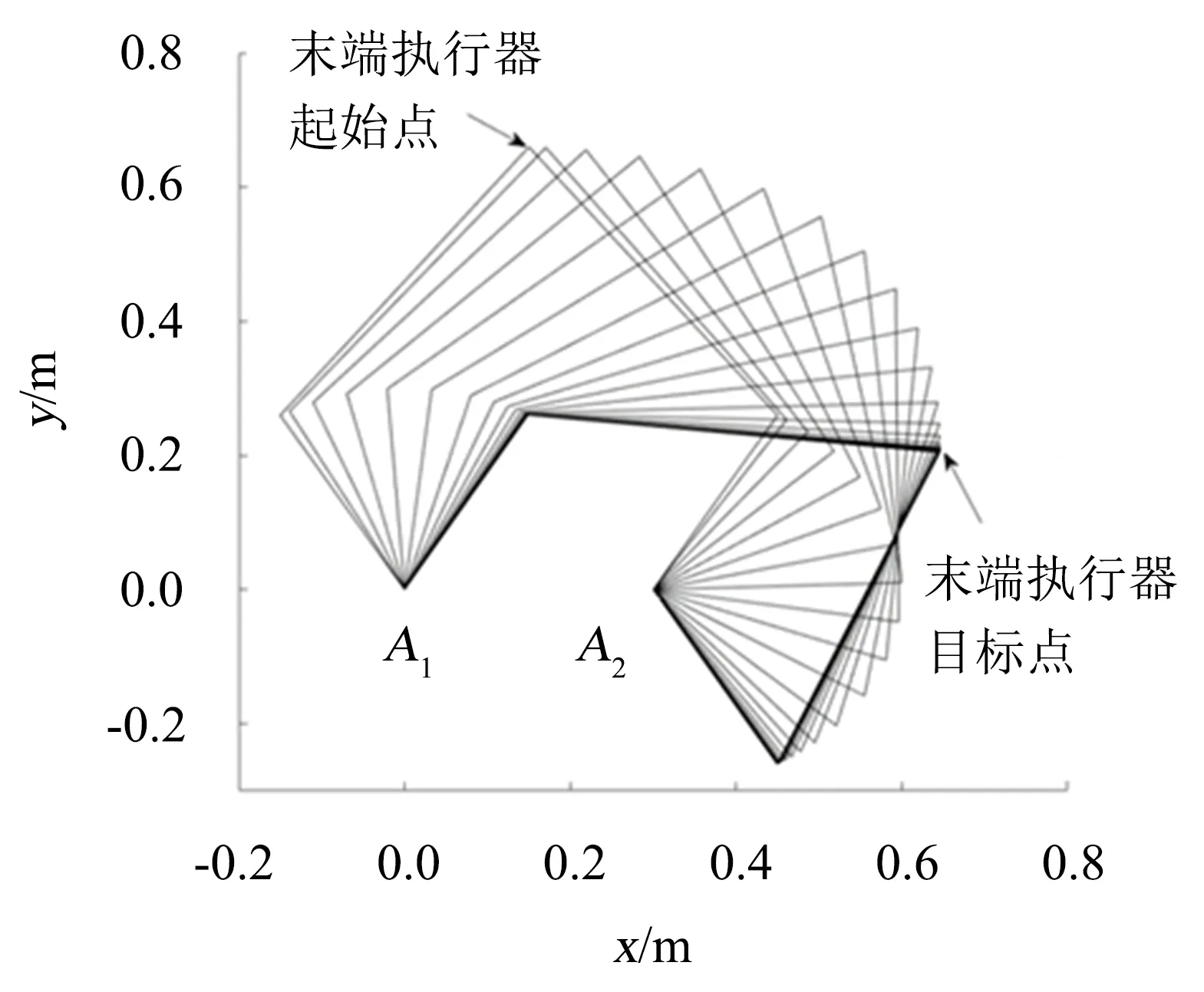
图8 系统构型变化过程Fig.8 Changing course of system configuration
4 结论
基于平面五连杆机构原理,设计具有两自由度的平面2RR并联机器人,实现在平面工作空间的快速分拣操作.利用第二类拉格朗日方程,并结合并联机器人闭链几何约束关系,建立了系统完全驱动形式的动力学方程.针对并联机器人动力学方程高度非线性和强耦合等特点,设计了基于干扰观测器的滑模控制方法,对并联机器人分拣操作的高速运动进行控制,利用李雅普诺夫稳定性判定证明所设计的控制方法是全局稳定的.数值仿真结果表明,通过常用的独立PD控制与所设计的滑模控制的对比,表明滑模控制能更快跟踪上期望的轨迹;在滑模控制基础上,增加干扰观测器对不确定干扰进行实时辨识估计,有效克服了滑模控制中的抖振问题和不确定干扰对高速运动并联机器人稳定性的影响.设计的基于干扰观测器的滑模控制方法计算量较小,具有较强的鲁棒性和实时性.

