一种基于阵列天线的卫星导航信号姿态谱估计技术

柳丰收,翟雄志,于 纯,张 建,程 铭,赵世佳

(中船航海科技有限责任公司,北京 100070)

0 引言

传统惯性导航系统(INS)存在累积误差随时间增大的缺点，且测量结果不属于同一坐标系，难以完成不同平台的姿态统一。全球卫星导航系统(GNSS)不仅可以完成定位、授时及测速，还可实现载体姿态测量,为船舶、飞机、导弹提供姿态数据，并且测量结果位于统一坐标系。从上世纪末，世界各研究机构就开始基于GNSS的姿态测量系统的研究，研究方向主要集中于多天线基线测量法，基线测量法的关键技术是载波整周模糊度解算，对此学术研究与工业生产多采用双频伪距法、模糊度函数法等方法。基线测量误差受基线长度及卫星DOP值影响，计算复杂度高且收敛慢。

在导航电子战领域，卫星导航接收机是恶意干扰的首要目标，利用阵列天线的空间滤波特性，在屏蔽干扰的同时可保留有用信号。同时，阵列天线还可完成干扰测向，利用阵列信号构建空间谱，通过空间谱极大值搜索获取干扰俯仰角信息。受此技术启发，如果已知信号方向，可对天线坐标系与卫星坐标系的相对关系(即天线姿态)进行计算。通过阵列信号分析，给出以天线姿态为变量的空间谱估计，建立了姿态空间谱估计(attitude spectrum estimation)技术，为阵列天线在卫星导航测姿技术领域的应用提供了理论支撑。

1 导航信号空间模型

1.1 导航信号空间模型

阵列信号表达式为:

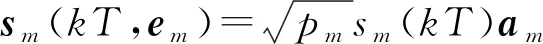
(1)

式中:为卫星信号编号，=0,…,-1(为卫星个数);为信号复包络;为采样点标号;为采样周期;位于天线坐标系，表示卫星信号方向矢量，位于卫星坐标系;为信号导向矢量，其第分量定义为：

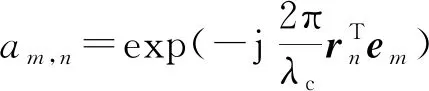
(2)

式中：为阵元编号，=0,…,-1(为阵元个数)；为信号波长；为信号功率；为阵元位置向量。天线坐标系与卫星坐标系的旋转关系即天线姿态。

1.2 天线坐标系下阵元坐标

以四元阵天线为例，建立阵元位置向量在天线坐标系下的数学表示，如图1所示。

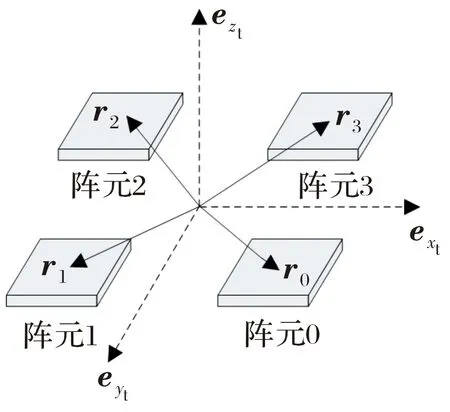
图1 天线坐标系

天线坐标系为：

={,,}

(3)

阵元位置矢量可以表示为：

=

(4)

式中：为天线坐标系下阵元坐标。

1.3 卫星坐标系下信号方向

卫星坐标系符合IERS规范，与CGCS2000定义一致。BDCS参考椭球如图2所示。

图2 BDCS参考椭球

卫星坐标系定义为：

={,,}

(5)

则第号卫星方向矢量在该坐标系下可表示为：

=()

(6)

式中：为信号在卫星坐标系下的单位方向矢量;为信号入射角度。

1.4 天线坐标系与卫星坐标系关系

根据坐标系变换理论，天线坐标系可通过卫星坐标系旋转得到，旋转可以分为3次，分别为绕轴旋转，绕轴旋转以及绕轴旋转，这3个独立旋转角称作欧拉角。以绕轴旋转为例，给出坐标旋转示意图如图3所示：

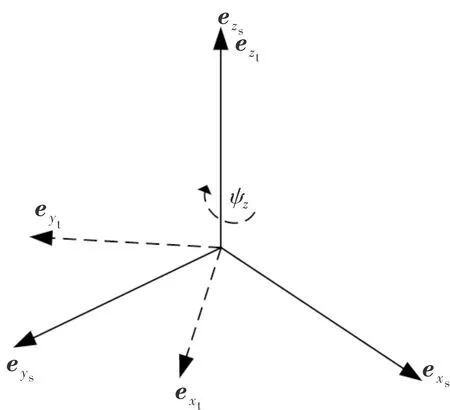
图3 坐标轴旋转

3次旋转矩阵分别为：

(7)

(8)

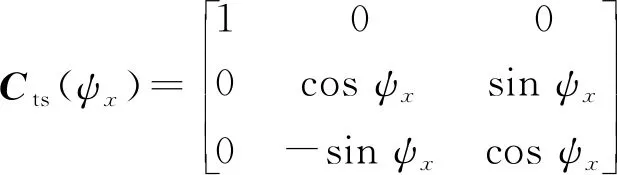
(9)

其中:()为绕轴逆时针旋转矩阵，旋转角度为；()为绕轴逆时针旋转矩阵，旋转角度为；()为绕轴逆时针旋转矩阵，旋转角度为。根据旋转关系得到天线坐标系与卫星坐标系的关系为：

=()

(10)

式中：()=()()()。

1.5 坐标旋转矩阵下信号模型

根据导航信号空间模型，将式(4)、式(6)及式(10)代入式(2)，得到含有天线姿态矩阵()的导向矢量(,)，其第分量可表示为：

(11)

综合信号包络与噪声后得到含有姿态信息的阵列信号模型：

(12)

式中：为噪声矢量;为热噪声标准差。

2 天线姿态谱估计

卫星导航信号到达地面功率非常低，往往低于噪声功率20～30 dB，为了进行姿态谱估计必须增强信号。为此提出阵列矢量跟踪环路,不同于传统意义上Spilker提出的多星矢量跟踪,采用矢量跟踪环路对阵列信号进行解调解扩及信噪比增强。以矢量跟踪输出信号为基础，提出基于多重信号分类(MUSIC)算法的单星观测姿态谱估计方法，进一步推广到基于正交投影算法的多星观测姿态谱估计方法。

2.1 矢量跟踪环路

矢量信号跟踪环路输入输出为矢量信号，每个分量对应一个阵元。取参考支路进行环路跟踪，再利用恢复的本地码与载波对其余支路进行载波与扩频码剥离，如图4所示。

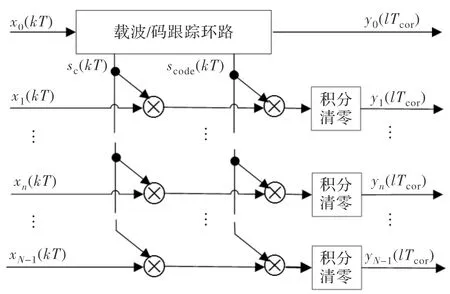
图4 矢量跟踪环路

其中第0支路进行环路跟踪，恢复出本地载波与本地码信号，利用该信号对各个支路进行相关解扩，积分清零器输出的相关值序列为：

(13)

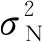
2.2 单星观测MUSIC姿态谱估计

MUSIC算法是一种经典超分辨率谱估计算法，常用来做频率与信号到达角估计。以基本MUSIC算法为蓝本，推导建立基于多重信号分类的姿态谱估计(MUSIC-ASE)。

以矢量跟踪环输出为阵列快拍的自相关矩阵：

=E[()()]

(14)

对式(14)进行特征分解，得到：

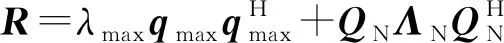
(15)

式中：为的最大特征值，对应信号能量;对应信号空间;特征值对应噪声能量;特征矩阵为噪声空间。理想情况下信号子空间与噪声子空间正交，可表示为：

(16)

实际工程中利用最小二乘法对式(16)进行变形，得到姿态谱函数：

(17)

式中：为天线姿态角;为已知信号方向。当接收机定位后，可获取卫星坐标系下的信号方向，通过最大值搜索便可获取天线姿态角。

2.3 多星观测正交投影姿态谱估计

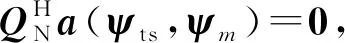
()=[(,),…,(,),…,(,-1)]

(18)

对其进行QR分解，得到：

(19)

根据矩阵理论，正交投影矩阵()将()沿着投影到上，从而避开的求解，即：

(20)

利用相关值序列估计出的正交投影矩阵为：

(21)

最终得到的多星观测正交投影法姿态谱为：

(22)

式中,‖‖是取矩阵的范数。当天线姿态变量等于天线姿态时，谱函数取得最大值。

3 仿真分析

影响姿态估计的主要因素包括观测卫星个数、信噪比、阵列孔径大小、卫星分布。以下针对这些因素进行仿真分析。

仿真中使用两种阵列，分别是9元圆阵与4元方阵。9元圆阵的阵元均匀分布于同一平面的圆周上，相邻阵元距离半波长，4元方阵的相邻阵元距离也是半波长。天线坐标系与卫星坐标系关系为：为10°，为20°，为30°。3颗卫星信号在卫星坐标系的俯仰方位分别为：卫星1(45°,0°)、卫星2(45°,120°)、卫星3(45°,240°)。姿态谱以最大值归一化，第一等高线下降0.5 dB，之后以3 dB下降。

实验1:理想情况与实际情况对比

采用9元圆阵，理想情况下信号导向矢量已知；实际情况中，采用信噪比为20 dB的相关值序列估计导向矢量如图5～图7所示。

图5 理想情况姿态谱

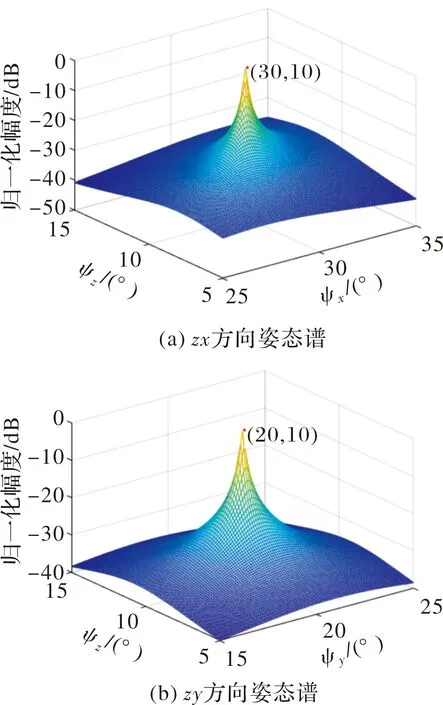
图6 实际情况姿态谱

图7 实际情况姿态谱等高线

对比实际与理想两种情况下的姿态谱，由于实际姿态谱估计使用带有噪声的导向矢量，从而造成谱峰钝化及能量泄露现象。图7为实际情况下姿态谱等高线，距离欧拉角真值越近,等高线越密集,说明谱峰越尖锐。

实验2:信噪比影响

在实验1的实际情况基础上，将信噪比减小到10 dB，其他条件不变实验结果如图8所示。

图8 10 dB信噪比姿态谱等高线

对比图8与图7可以看出：信噪比降低后欧拉角真值附近等高线变稀疏，说明降低信噪比会增加谱峰钝化，因此在做姿态谱估计时应选取信噪比较强的卫星。

实验3:卫星个数影响

在实验1的实际情况基础上，只利用1号星估计姿态谱，对比卫星个数的影响如图9所示。

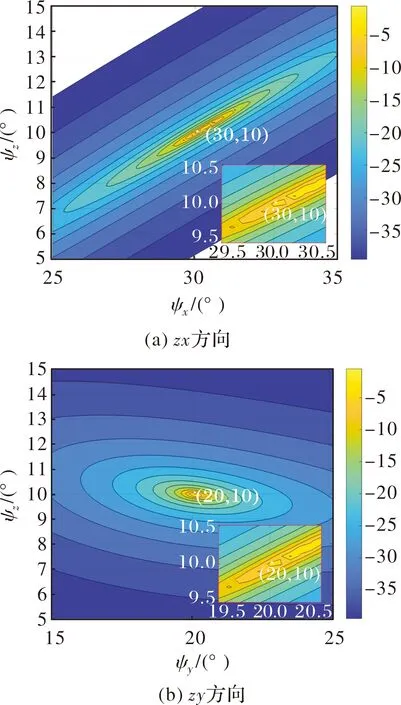
图9 单星观测姿态谱等高线

对比图9与图7可以看出：单星观测引起谱峰畸变、谱峰分裂，姿态谱沿着某些方向被拉长。说明单星观测引起谱峰模糊，这是因为单星观测所利用的卫星方向信息较少所至。

实验4:阵列孔径大小影响

在实验1的实际情况基础上，以4元方阵代替9元圆阵，通过减小阵元个数分析阵列孔径大小对姿态谱的影响如图10所示。

图10 小阵列孔径姿态谱等高线

对比图10与图7可以看出：减小阵列孔径后，在欧拉角真值附近等高线变稀疏，谱峰钝化，谱峰分辨率明显下降。

实验5:卫星分布影响

在实验1的实际情况基础上，将卫星方位角集中，由原来间隔120°减小为30°，如图11所示。

图11 卫星方向集中姿态谱等高线

对比图11与图7可以看出：观测卫星集中后引起姿态谱畸变并伴随谱峰分裂。这与单星观测情况类似，单星观测可以看作多星集中观测的极限。

4 结论

根据阵列信号空间谱分析理论提出基于阵列天线的卫星导航信号姿态谱估计技术，将阵列天线测姿问题转化为姿态谱的最大值问题。通过姿态谱的计算得到的天线姿态天然位于卫星坐标系，从而将不同接收机置于同一坐标系。通过仿真分析了影响姿态谱估计的主要因素及产生原因，得到提高姿态谱估计的基本原则：1)选用信噪比强的卫星;2)选用空间分布远且分布均匀的多颗卫星；3)增大阵列孔径。