3维非定常Navier-Stokes方程组高效全离散有限元方法研究进展∗

何银年，冯新龙

(1.新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830017；2.西安交通大学 数学与统计学院，陕西 西安 710049)

0 引言

3维非定常不可压缩Navier-Stokes方程组（简称N-S方程组）[1−14]:

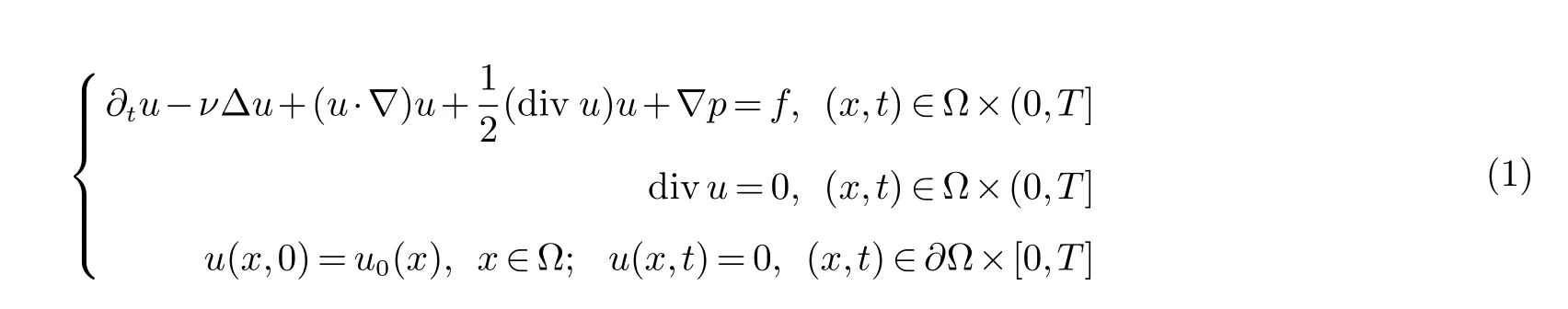
其中:u=(u1(x,t),u2(x,t),u3(x,t))表示速度向量,p=p(x,t)表示压力,f=f(x,t)表示给定外力,u0(x)表示初始速度,ν ＞0 表示粘性系数及T ＞0表示大时间区间长度,Ω ⊂R3表示有界区域.3维非定常不可压缩N-S方程组的初边值问题是描述不可压缩流体运动最一般的规律,是典型的非线性问题,在工程应用和非线性科学研究方面具有广泛的应用背景和重要的科学意义.然而,由于人们对N-S方程组的非线性现象本质和解的特性认识有限,使得数值求解N-S方程组成为一种十分重要的研究手段.但数值求解N-S方程组面临三大困难:即如何处理不可压缩约束条件div u=0,强非线性(u·∇)u和长时间区间[0,T]积分的问题[1−3].

对于依赖于空间时间变量(x,t)的非定常N-S方程组的数值求解,人们首先是设计空间变量离散化,考虑半离散解(uh(x,t),ph(x,t))所满足的近似N-S方程组,然后再考虑时间变量离散化,即全离散解所满足的有限维近似N-S方程组;或者相反先设计时间变量离散化,考虑半离散解(un(x),pn(x))所满足的近似N-S方程组,然后再考虑空间变量离散化,即考虑全离散解所满足的有限维近似N-S方程组.由于篇幅有限,本文仅考虑前一种情形,且仅考虑有限元的空间离散情形,不考虑有限差分方法、有限体积元方法、谱方法等其它方法的空间离散化情形.在设计空间变量离散化时,人们首先考虑的是如何克服不可压缩约束条件div u=0的困难.通常采取的方法是:(1)设计满足inf-sup条件的协调或非协调的有限元空间对(Xh,Mh)[1−8,13];(2)对一般的有限元空间对(Xh,Mh)构造稳定化的弱变分形式[15−18];(3)设计满足不可压缩约束条件div uh=0的有限元空间对(Xh,Mh)[19−22].考虑文章的篇幅限制,本文仅考虑满足inf-sup条件的一阶协调有限元空间对(Xh,Mh)情形.

非定常N-S方程组在经过空间变量离散化后,得到关于时间变量的一个非线性常微分方程组.因此为了得到非定常N-S方程组的数值解,还需要对时间变量实施有限差分离散化.为了克服长时间区间[0,T]积分的困难,需要设计一个大时间步长的有限差分数值方法.高阶时间精度的离散差分格式可以使得时间离散步长取大一些.考虑到非定常N-S方程组解的正则性限制,人们通常选取时间二阶精度的差分离散化格式.时间二阶精度的离散格式有全隐格式(例如Crank-Noclson差分格式[7]),半隐格式(例如Crank-Noclson外推差分格式[23−25]) 和隐式/显式差分格式(例如Crank-Noclson/Adams-Bashforth差分格式[26−27])等.众所周知,尽管二阶精度的全隐格式是无条件稳定的,但是对于每个时间层n,需要求解关于的非线性方程组,人们承受不了这个巨大的计算量耗费.其次时间二阶精度的半隐离散格式也具有线性化和无条件稳定的优点,克服了非线性的困难,但是对于每个时间层n,求解关于的线性方程组时,需要求解变系数矩阵的大型代数方程组,即其系数矩阵仍然依赖前两步的速度向量人们仍然难以承受这个大的计算量耗费.最后,用时间二阶精度的隐式/显式差分格式求解时,对每个时间层n,仅仅需要求解常系数矩阵的大型代数方程组.这样既克服了长时间积分和非线性的困难,又花费较少的计算量耗费.因此,把空间离散的满足inf-sup条件的一阶协调有限元空间对(Xh,Mh)方法和时间离散的二阶精度的隐式/显式差分格式结合起来,就得到求解非定常N-S方程组的高效有限元方法.对于时间二阶精度的隐式/显式差分格式,除了Crank-Nicolson/Adams-Bashforth(CN/AB)差分格式,还有二阶后差隐式/显式差分格式或称Gear外推差分格式[28−29]等可以被应用于求解非定常N-S方程组.

众所周知,尽管时间二阶精度的CN/AB全离散有限元方法吸引了众多学者的极大兴趣,然而在以往数值分析方面,许多学者认为即使在初值足够光滑的条件下,该数值方法的CFL稳定性和收敛性条件都要求时间离散步长τ严格地依赖于空间离散尺度h.在文献[3]中,Marion及Temam提出了下列的稳定性和收敛性条件:

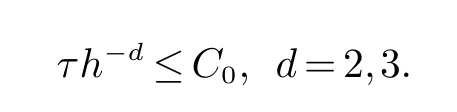
其中d=2,3表示空间区域Ω的维数.最近,Tone[27]给出了下列的收敛性条件:

另外,在修正的CN/AB情形下（非线性项和压力项都是显式的）,Johnston及Liu[30]提出了下列的稳定性条件:

最近,He及Sun[26]证明了求解二维非定常N-S方程组时稳定性和收敛性条件是τ ≤C,即是几乎无条件稳定和收敛的.此外,He及Sun[26]也证明了下列的收敛性结论:对每一时间步tn∈(0,T],全离散解满足下列的收敛率

其中:σ(t)=min{1,t},κ是一个依赖于参数(ν,Ω,T,u0,f)的一般性常数.这里数值速度在L2范数意义下关于时空变量(x,t)达到了最优收敛阶,数值速度和压力在H1-L2范数意义下关于时间步长τ没有达到二阶最优收敛.

在最新的研究中,He,Zhang及Zou证明了求解三维非定常N-S方程组时稳定性和收敛性条件是τ ≤C,并且也证明了下列的收敛性结论:对每一时间步tn∈(0,T],全离散解满足下列的收敛率

本文第一节主要介绍3维非定常N-S方程组有关数学描述和已有的存在性、唯一性和正则性结论.第二节主要介绍3维非定常N-S方程组有限元空间离散的有关数学描述和已有的收敛性和稳定性结论.第三节主要介绍3维非定常N-S方程组的时间二阶精度的CN/AB全离散有限元方法的有关数学描述和最新收敛性结论.第四节给出本文主要结论.

1 3维非定常N-S方程组的有关数学描述及预备知识

令Ω ⊂R3是具有Lipschitz连续边界的有界单连通区域,Banach空间Lp(Ω)是区域Ω上的p次Lebesgue可积函数全体,且赋予范数

为了书写简便,我们常常利用记号u(t)表示函数u(x,t).对于p=2,L2(Ω)是Hilbert空间且赋予内积和范数:

进一步,我们也引进下列Hilbert空间H1(Ω),H2(Ω):

以及下列内积和范数.

由Green公式,可以导出(1)的变分形式:求u ∈L∞(0,T;L2(Ω)3)∩L2(0,T;X) 及p ∈L2(0,T;M),使得对任意(v,q)∈X×M 满足

其中:X=(H10(Ω))3,M=L20(Ω)={q ∈L2(Ω);∫Ωq(x)dx=0},以及

如果(u,p)满足(4),被称为非定常N-S方程组的弱解.此外,如果弱解(u,p)还满足正则性u ∈L∞(0,T;X)∩L2(0,T;(H2(Ω))3∩X)及p ∈L2(0,T;H1(Ω)∩M),则(u,p)被称为非定常N-S方程组的强解.目前,对于一般的数据(ν,Ω,u0,f,T),非定常N-S方程组的弱解的唯一性和强解的存在性还是一个未解的重大难题[1−3,8−12,14].

本文中我们关于问题(1)中已知信息u0及f(t)作下列假设.

假设(A0):初始速度u0∈H2(Ω)3∩X且满足∇·u0=0,以及外力项f满足

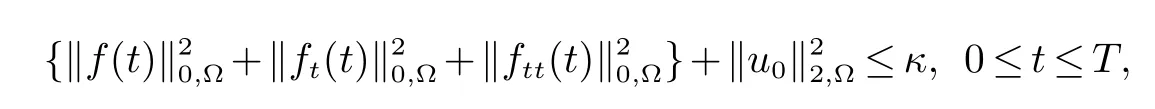
这里κ及以下κ0被用来表示依赖于数据(ν,Ω,T,u0,f)的正常数.

进一步,如果3维区域Ω是一凸多面体或边界∂Ω是C1,1的,则下列的正则性假设成立.

假设(A1):如果f ∈(L2(Ω))3,则Stokes方程组：

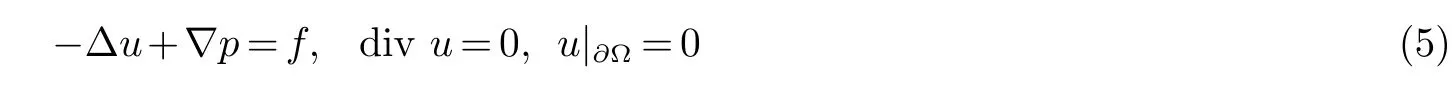
允许有唯一解(u,p)满足下列正则性：

其中c0=c0(Ω)是依赖于Ω的常数.

为了以后研究非定常N-S方程组解的正则性及其数值解的收敛性,我们需要引进下列Gadliardo-Nirenberg不等式[1−7]:

其中c1和γ0为依赖于Ω的常数.利用不等式(6)～(7),我们可以导出非线性算子B(w,u)的下列关系式:

其中N0=N0(Ω)是依赖于Ω的常数及

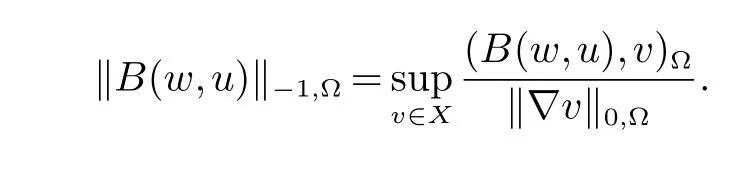
应用(8)并在(4)中取检验函数(v,q)=(u,p),我们得到下列的关系式:

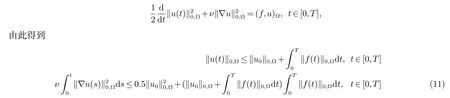
为了进一步得到解的正则性结论,我们需要对弱解(u,p)做出进一步的假设.

假设(A2):假定问题(4)的弱解(u,p)满足

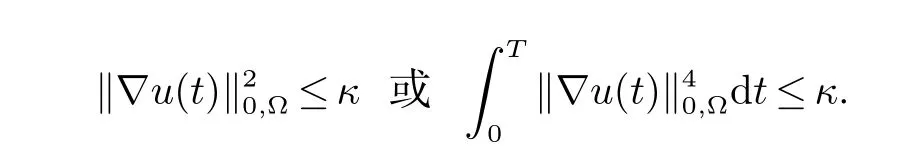
利用假设(A0)～(A2)及估计式(8)～(10),可以导出(u,p)如下的正则性结果[4].

定理1如果假设(A0)～(A2) 成立,则问题(4)的弱解(u,p)满足:

2 3维非定常N-S方程组的有限元离散化

为了方便,本文仅考虑3维有界的凸多面体区域Ω,对Ω进行拟一致正则的四面体网格剖分四面体单元K的直径表示为hK,并定义网格尺度为引进有限元空间Xh⊂X及Mh⊂M满足下列的一阶逼近和inf-sup条件假设[4].

假设(A3):假定有限元空间对Xh×Mh满足

(1) 对每一v ∈H2(Ω)3∩X及q ∈H1(Ω)∩M,存在逼近函数πhv ∈Xh及ρhq ∈Mh使得

成立及inf-sup条件:对每一qh∈Mh,存在vh∈Xh,vh/=0 使得

成立,其中c2及β是依赖于Ω的正常数.

根据文献[2,32-33],存在一系列有限元空间对Xh×Mh满足假设(A3),比如P2-P0元:

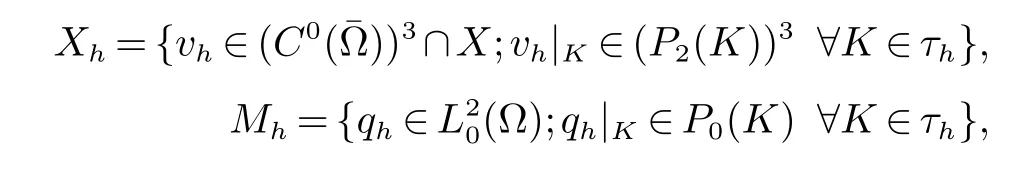
由于有限元空间对Xh×Mh满足假设(A3),可以定义有限元空间

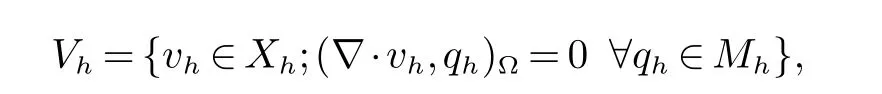
及离散Stokes算子Ah=-PhΔh,其中Ph是由(L2(Ω))3到Vh的L2-投影算子,满足

以及离散拉普拉斯算子-Δh被定义为

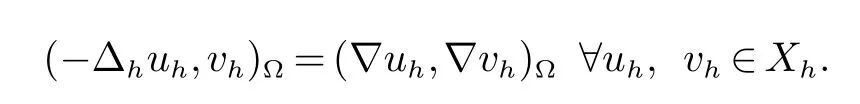
由此可以定义离散的Sobolev范数

根据离散Stokes算子Ah的定义,结合(7),可得下列离散Gadliardo-Nirenberg不等式[4]:

于是可以由(14)推出非线性项B(wh,uh)满足下列的有界性:

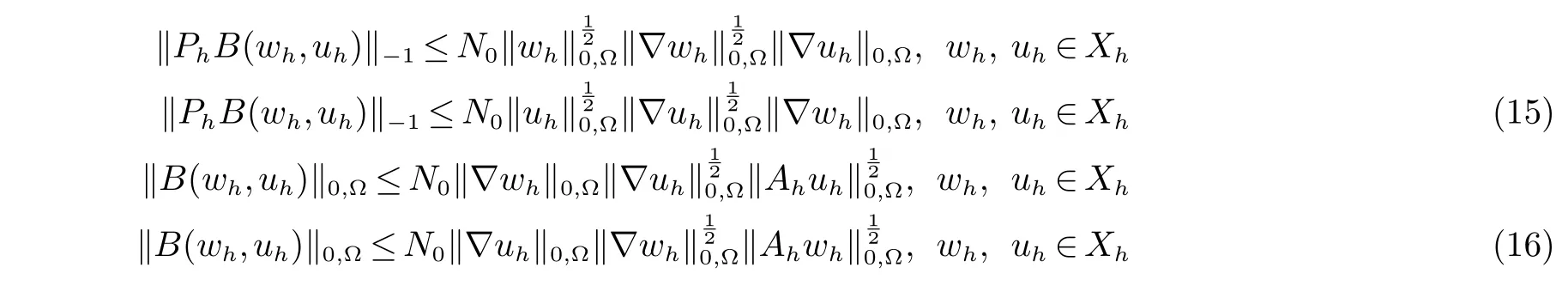
现在我们定义非定常N-S方程组(4)的有限元变分形式：对每一t ∈(0,T] 求(uh(t),ph(t))∈Xh×Mh使得对每个(vh,qh)∈Xh×Mh满足

其中uh(0)=Phu0.在(17)中,取(vh,qh)=(uh,ph)及利用(8),我们可得到

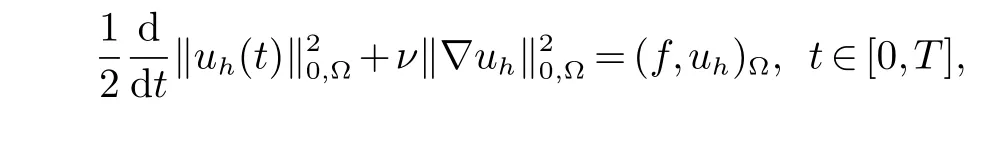
再利用假设(A0)～(A3)和B(w,u)性质及定理1关于(u,p)的正则性结论,我们可以导出(uh,ph)关于(u,p)的下列误差估计结果.

定理2如果假设(A0)～(A3)成立,则问题(17)的有限元解(uh,ph)满足下列误差估计:

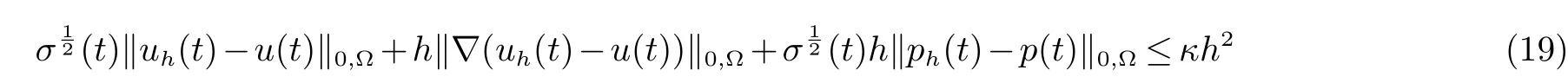
由于假设(A2)～(A3),(18)～(19),我们可以证明有限元解(uh,ph)满足下列稳定性[7]:

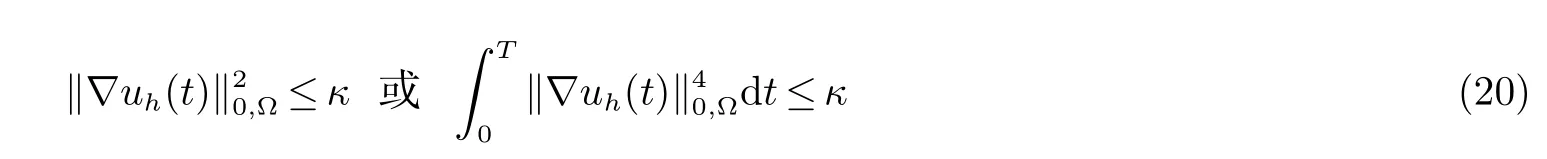
最后根据(15)～(20),我们可以证明对于每一t ∈(0,T],有限元解(uh,ph)满足下列进一步的稳定性:

上述稳定性结果是进行全离散有限元解的基础保障.

3 3维非定常N-S方程组的NS/AB全离散有限元解及其最优误差估计

成立.利用不等式关系(8),(15)～(16),(24),定理2,有限元解(uh,ph)的稳定性以及归纳法原理,可以得到满足误差估计结果.

4 结论

求解三维非定常N-S方程组的CN/AB全离散有限元方法在每个时间步都是解线性方程组(Stokes方程组),对每一时间层n,其系数矩阵是固定不变的.在该数值格式中线性项用隐式格式离散以增加其格式的稳定性能,非线性项用显式格式离散以保证格式的简单性.此外,现有研究分析表明该方法是几乎无条件稳定和收敛的,并且关于时间步长τ是最优阶收敛的,即该方法不要求时间离散步长τ不随着空间网格尺度h的缩小而影响时间步长τ的选取,从而允许选取大的时间步长τ,因此该方法也克服了求解3维非定常N-S方程组的强非线性和长时间区间积分的困难,另外由于使用满足inf-sup条件的协调有限元空间对Xh×Mh克服了不可压缩约束条件的困难.综上所述,CN/AB全离散有限元方法是求解三维非定常N-S方程组的高效有限元方法.