曲面上对流-扩散-反应方程的两种稳定化混合有限元方法的数值比较∗

金孟晴，冯新龙†，何银年,2

(1.新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830017；2.西安交通大学 数学与统计学院，陕西 西安 710049)

0 引言

对流-扩散-反应方程是基本的动力学方程,它描述了三种不同的物理现象：对流、扩散和反应[1−2].对流扩散现象包括河流污染、空气污染、污染物在核废料污染中的分布等.随着数学和工程研究的发展,人们需要使用更加复杂的数学模型来描述自然界中的一些物理现象,这就使得研究者们将注意力集中在曲面问题的建立与求解上.因此,曲面偏微分方程的重要性越来越突出.

我们知道求解曲面椭圆方程的有限元方法可以追溯到1988年[3],作者用三角剖分来离散曲面,此后相继出现求解曲面方程的方法.在流体力学中,一些文献介绍和总结了两相不可压流的数值模拟方法.在生物学领域,一些生物学家用曲面对流和扩散现象来描述生物膜上的物质转移[4−5]、种群迁移以及细菌在生物膜上的聚集现象[6−7].在大多数实际应用中,都需要求解曲面对流-扩散-反应方程.然而,用解析的方法在曲面上求解此类方程是一个巨大的挑战,尤其是对流占优问题的相关求解.尽管一些学者对对流占优问题的数值逼近做了大量的工作,但仍然存在一个问题,即如何找到一种精确、稳定、快速的数值方法对其进行模拟.

对流占优问题,使方程有了双曲方程的性质,这让求解变得更加困难,用一般的方法,比如标准的有限元方法、有限差分方法会导致所得到的解产生非物理震荡.只有当网格剖分的足够细时,解才会相对稳定.但对于高维问题,网格剖分较细会导致大的计算量和存储空间.因此,我们希望设计一种算法,即使网格尺寸稍大,也能克服上述问题.在本文中,我们采用混合的一阶形式来近似对流-扩散-反应方程，其中两个变量使用有限元对(P1-P1),根据平面微分方程中运用的稳定化思想[3,8−13],文中使用混合稳定化方法消除对流占优情况所产生的非物理震荡.最后进行了数值实验,来验证两种算法的有效性并得到了相应的结果.

1 预备知识

在这一部分,我们将介绍一些曲面的预备知识,比如曲面算子的一些符号和相应的Sobolev空间以供后面使用.此外,还推导了曲面上对流-扩散-反应方程的混合弱形式.

1.1 曲面算子

假设Γ ⊂R3是一个开区域,Γ ⊂Ω 是一个紧致曲面,可以用一个函数的零水平集φ(x)∈C2(Γ)定义,使得

对于充分光滑的函数f:Γ →R 在曲面上某一点x ∈Γ 的切向梯度可以定义为

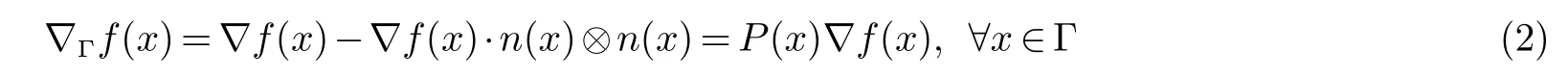
这里,P(x)=I-n(x)⊗n(x),∇表示平面上标准的梯度算子,其中曲面法向n定义为

函数φ 满足∇φ(x)/=0.

同样的,曲面上的散度算子F(x)=(F1(x),F2(x),F3(x))∈R3可以被定义为

自然的,Laplace-Beltrami 算子可以定义为

1.2 Sobolev 空间

假设Γ 是属于C2的一个曲面,Lp(Γ) 是可测量函数f:Γ →R 的空间,则我们将Sobolev 空间Wr,p(Γ) 定义为

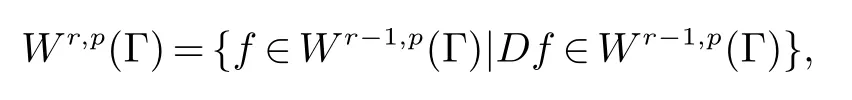
这将用于推导对流-扩散-反应方程的混合形式.

1.3 曲面对流-扩散-反应方程

我们所研究的问题是以下的对流-扩散-反应方程:在Γ上找到p,使得

其中:ε ＞0 是扩散系数,α ∈W1,∞(Γ)3是对流项且在Γ 上满足∇Γ·α=0,µ＞0 是反应系数,f 是体积力且属于L2(Γ).

引理1[14]假设α 在曲面Γ 上是给定的无散度速度场,即满足∇Γ·α=0.此外,如果α 和µ 满足下式,则方程(12) 有弱解

我们思考(12) 的变分形式:找到p ∈H1(Γ),使得

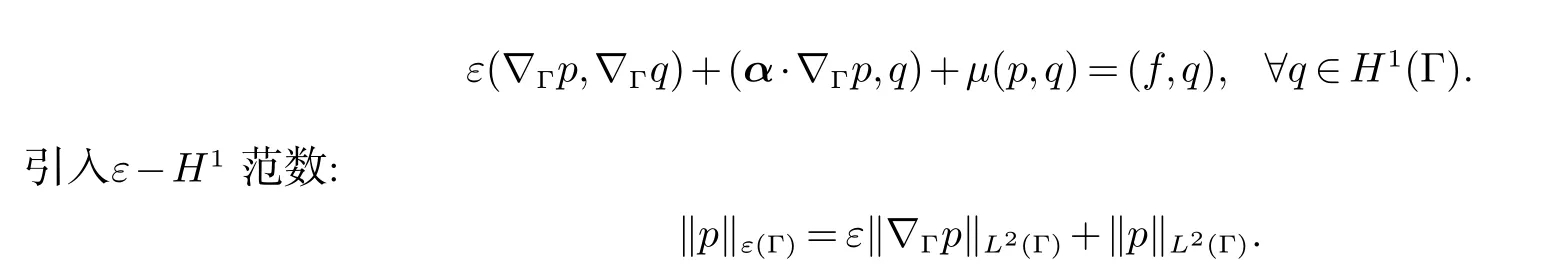
定理1[14]假设Γ ∈C2且p ∈H2(Γ),我们得到

算法一:定义扩散通量为vd:=-ε∇Γp,因此在Γ 上(12) 变成

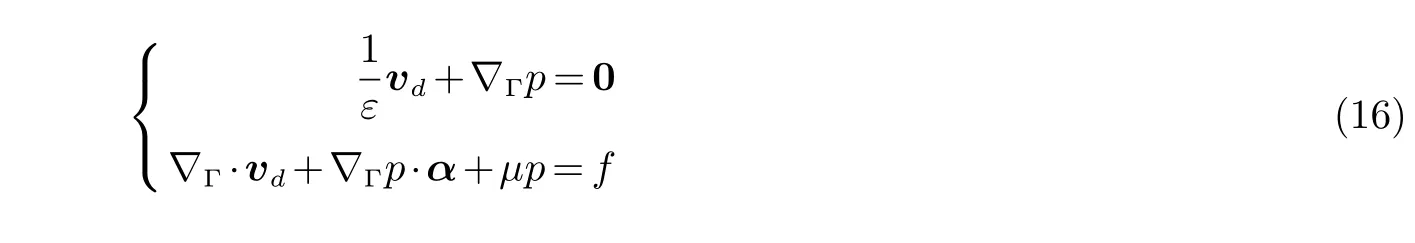
(16) 的弱解是:找到(vd,p)∈V×Q:=H(∇Γ·;Γ)×L2(Γ),使得

对所有的(w,q)∈V×Q.

算法二:我们定义总通量为v:=-ε∇Γp+αp,因此在Γ 上(12) 变成

(18) 的弱解是:找到(v,p)∈V ×Q:=H(∇Γ·;Γ)×L2(Γ),使得

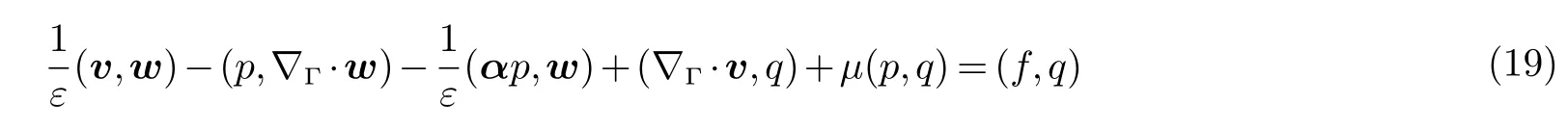
对所有的(w,q)∈V ×Q.

引理2[15]若α 和µ 满足(13) 且方程(12) 有唯一的弱解,使得

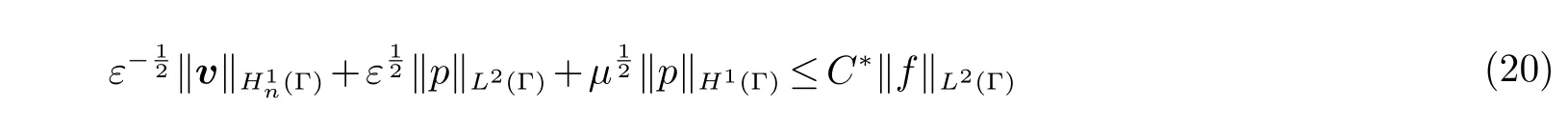
其中:C∗是一个正常数.

注1:使用Lax-Milgram 引理,可以证明(12)具有唯一的弱解p ∈H1(Γ).因此,问题(16)或(18)的任何一个解都是(12) 的弱解,反之亦然.

2 稳定混合有限元方法

在这个部分,将介绍一种稳定混合有限元方法.首先,我们用一致的分片三角形来逼近光滑曲面Γ.因此,由近似曲面Γh引入的几何误差一般为O(h2),其中h 是分片三角形Γh的网格尺度.

我们选择一系列的点{x1,x2,···,xNp} 生成一个不重叠的三角形单元{e1,e2,···,eNe},由这些单元近似光滑曲面所组成的曲面Γh被定义为:

其中:Ne和Np分别表示单元和节点的个数,h=max{h1,h2,···,hNe} 是离散曲面网格的大小.对于离散曲面Γh上的任意点x,有光滑曲面Γ 上的点a(x) 与之对应,满足以下的映射关系

其中:d(x) 是一个定向距离函数并且满足|d(x)|=dist(x,Γ),∇d(x)=n(a(x)) 和|∇d(x)|=1,详细介绍可参阅文献[16].

引理3[17]光滑曲面Γ 的定向距离函数d(x) 满足以下估计

其中:C∗是一个正常数.

对于曲面Γ 上定义的函数，我们可以将它投影到近似曲面Γh上

定理2[3]假设v 是v−l∈H1(Γ) 在Γh上的投影,则有下列范数等价

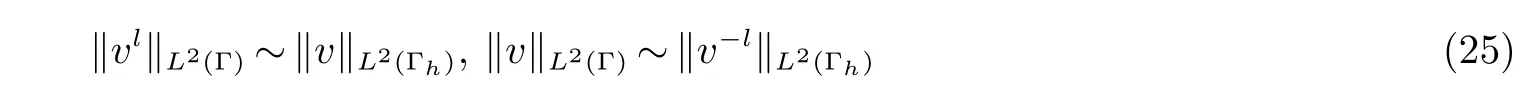
对于上面定义的有限元空间,我们引入了基于曲面Γh的有限元空间,其中通量变量v 的离散子空间为:

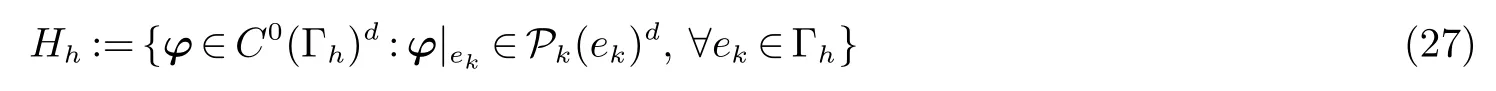
标量变量p 的离散子空间为:

我们可以得到(19) 的离散变分形式如下:找到(vh,ph)∈Hh×Qh,使得

本文在(17) 式的离散变分形式中加入了稳定项,此时,求解的离散形式变为:找到(vdh,ph)∈Hh×Qh,使得

本文在(29) 式上加入了稳定项,此时,求解的离散形式变为:找到(vh,ph)∈Hh×Qh,使得

其中:δ ＞0 是正的常数.

此外,我们在离散空间中定义算法一和算法二的范数:

算法一范数:

定理3设A(·,·)Γh是(30) 中的双线性形式.存在一个不依赖于ε,µ 和h 的正常数C,使得

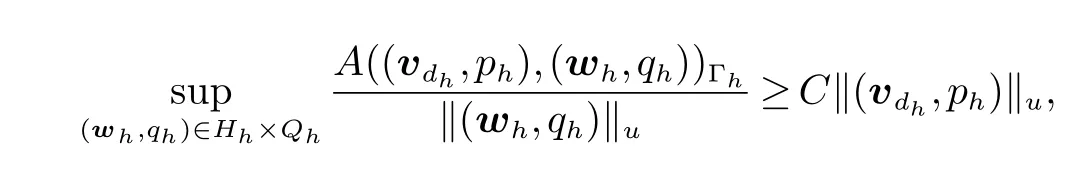
其中:(wh,qh)∈Hh×Qh.

证明 用A(·,·)Γh的定义,Cauchy-Schwarz 和Young 不等式,我们得到

注2:离散形式(32) 的稳定性在[15]中已被证明.

3 数值算例

在这部分,我们展示了几个数值实验的结果,以说明所提方法的有效性.

例1在球面上考虑问题(12).

球面隐函数为:

我们选择连续的精确解如下,右端项f 由精确解给出

这个实验的目的是检验方法的有效性.我们将取扩散系数ε 和反应系数c 等于1.为了计算误差阶,我们取网格剖分和自由度分别为h=0.2,0.1,0.05,0.025和447,1 703,6 718,26 562,所得到的结果如图1所示.从图1中,我们可以看到变量的L2范数的收敛阶是2阶,我们分别运用中间变量的定义将p 的H1范数的收敛阶提升到2阶,所得到的结果如图1所示,这些结果与我们所做的理论分析一致.

图1 比较两种方法中p 和v 的误差阶

例2在流行上,对方程(12),考虑扩散系数是ε=10−3的解间断问题.

曲面隐函数表达式为:

在这个实验中,我们所采用的精确解和对流项与例1相同,测试两种混合形式的对流占优问题.我们发现当ε 较大时,对流-扩散-反应方程具有光滑的精确解.然而,当ε 取值较小时,精确解的函数值是具有大梯度变化的对流占优问题.

我们在三角曲面网格上求解这个问题,图2是所得到的数值模拟结果.从图2中可以发现当ε=10−3时,其解在心型区域的中心上有非物理震荡现象.由于曲面的曲率不一样,在曲率大的地方模拟的效果比曲率小的部分差一些,且误差也较大.在这个数值实验中,我们将δ 设为1,并且采用相同的自由度求解此问题.由实验结果可知,我们的方法可以成功地捕获解的大跳跃,模拟效果较好.对比这两种方法可知算法二（运用全局中间变量）较好.

图2 当ε=10−3时,心型区域上两种混合形式的比较

4 结论

本文拓展并分析了两种稳定的混合有限元方法来求解曲面对流-扩散-反应方程.在给出稳定性分析外,还给出了一些数值实例,验证了已知理论的结果.采用这两种方法不仅可以有效地避免非物理震荡问题,而且提高了∇Γp 的精度.在文中还可以探讨高斯曲率、平均曲率等对其方程求解时的影响,今后将是我们的研究重点.