指向数学建模的数学应用课《三角测量》教学设计

王丽

◆摘  要：数学模型搭建了数学与外部世界联系的桥梁，是数学应用的重要形式，是应用数学解决实际问题的基本手段，也是推动数学发展的动力。本文以执教的三角函数应用课《三角测量》为例，讲述了如何在数学应用课中培养学生数学建模的核心素养，引领学生用数学的眼光观察世界、用数学思维思考世界、用数学语言表达世界。

◆关键词：数学建模;数学应用;三角测量

一、结合学情，预设学习目标

本着高中数学课程应面向全体学生，实现人人都能获得良好的数学教育，不同的人在数学上得到不同的发展的原则，我将本节课的学习目标预设为：

1. 我能够应用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的生活实际问题;

2. 我会从实际背景中提出问题、分析问题、建构数学模型、应用数学知识计算，进而解决问题;

3. 我要提高自己分析和解决实际问题的能力、动手操作的能力以及用数学语言表达和交流的能力，增强自己应用数学的意识，培养自己数学建模能力。

二、依据学情，预设重难点

根据我所教学生的实际情况，我预设本节课的重点和难点如下：

学习重点：利用正余弦定理解决实际三角测量问题

学习难点：在测量过程中，感受并抽象出数学建模过程，体会数学建模思想。

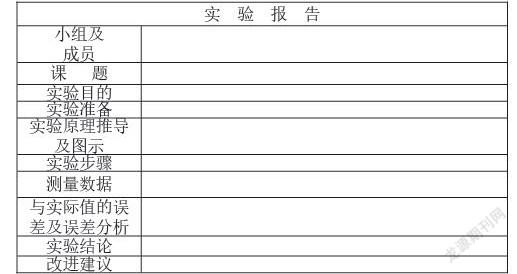
三、以生为本，定制实验报告

为了激发学生学习数学的兴趣，我依据组内异质、组际同质的原则把全班同学分成七组，不指定测量内容，不提供测量工具，充分发挥他们的想象力自定测量对象，如实填写实验报告，并在《三角测量》展示课上分享感悟。

我的设计意图是：让学生们自选情境、提出问题、建立并求解模型，检验和完善模型的数学建模过程。

四、精彩纷呈、进行课堂展示

1. 精彩励志、引入课堂

我以这段话“如果任何事物都保持一成不变，让我们如何期待生命的美好，所以生活需要惊奇、需要改变，我们开始探寻，追求完美，一直在努力，即使经历了无数次的否定，我们依旧坚持缔造卓越，只为可以成就他人，赏悦自己”的励志视屏引入展示课堂。

2. 你展示、我倾听

腾飞二组的展示形式是讲解自制的PPT。他们的分工是：组长是申尉孜，测量人员是：魏斌、杨昌蒙和申尉孜，计算：祖大元;解说：舒成敏;拍摄：方俊徽。他们的过程是：经过讨论，确定测量对象是草坪面积，确定测量方案;进行实地測量;他们的测量工具有计算器、百米尺。具体的测量步骤是：

（1）利用百米尺测出三边距离并记录

（2） 多次测量，减小误差

（3）根据所学知识整理数据，得出最终结果。

（4）要求：测量过程中不能践踏草坪。

（5）结合实地测量，画出简图如：

测量的数据是：a≈16.43m， b≈10.28m， c≈8.40m，

运算过程是：

先由余弦定理得cosA=[b2+a2-c22bc]=[10.282+8.402-16.4322×10.28×8.40]≈[-2750]，再由同角三角函数的基本关系式中平方关系可得：sinA≈[177150]，最后由面积公式可以得出：S[ΔABC]=[12]bc sinA=[12][×10.28×8.40×][177150]=[43177150]≈36.12m[2]

分析误差：测量工具步精确，应该使用更加精确的测量工具进行测量。

导数一组自称他们测量的是学校里非常美观的地方——学校绿化带的对角线长度。首先他们用视频展示测量的进程：计划——讨论——记录——第二次测量与记录——在展示板上画出示意图，经过测量得到以下测量数据：

3. 我们来探究

热情展示后必须要进行沉浸式的充分思考才能激发学生的数学思维，因此接下来我设计了几个数学探究活动。

探究1：倾听完各小组的展示，并结合课本P11-18页的例题，请大家探究可以归纳为哪些三角测量模型？并在各组的展示板上画出相应的数学图形。

探究2：回顾所经历的的测量过程，请归纳数学建模的步骤，并用思维导图画出来。

探究3：为了测定河对岸两点A、B间的距离，在岸边选定1公里长的基线CD，并测得[∠]ACD=90[°] [∠]BCD=60[°] [∠]BDC=75[°]

[∠]ADC=30[°]

（1）求A、B两点的距离;

（2）求解该题运用的哪种三角测量的模型？

五、教学感悟

《普通高中数学课程标准》要求我们要用教材去教，即通过高中数学课程的学习，学生能有意识地用数学语言表达现实世界，发现和提出问题，感悟数学和现实之间的关联;学会用数学模型解决实际问题，积累数学实践的经验;认识数学模型在科学、社会、工程技术诸多领域的作用，提升实践能力，增强创新意识和科学精神，提升了同学们团队合作、有效表达的综合能力。