基于光流矢量行波分离的相关加权逆时偏移成像
解闯, 宋鹏,2,3*, 邹志辉,2,3, 谭军,2,3, 王绍文, 赵波,2,3
1 中国海洋大学海洋地球科学学院, 青岛 266100 2 青岛海洋科学与技术试点国家实验室, 海洋矿产资源评价与探测技术功能实验室, 青岛 266100 3 中国海洋大学海底科学与探测技术教育部重点实验室, 青岛 266100
0 引言
逆时偏移起源于20世纪80年代(Whitmore,1983;Baysal et al.,1983;McMechan,1983),其基于双程波波动方程成像,能适应任意复杂速度模型,无成像角度限制,且理论上还可对回折波、棱柱波、绕射波、多次波等进行成像(杨仁虎,2021a),是当前公认的高精度成像算法之一.然而,由于逆时偏移需要基于双程波方程进行波场延拓,其在地震波传播到反射界面时会产生背向反射,而常规互相关成像条件不加以区分地将所有的震源正传波场与检波点反传波场直接应用于成像(杜启振等,2013;Chen and He,2014;杨仁虎,2021b),这会不可避免地产生大量的低波数偏移噪声.
目前主要发展了三类方法用于压制逆时偏移中的偏移噪声.第一类是压制背向反射方法,其通常采用无反射声波方程进行成像.Baysal等(1984)首先提出了基于常波阻抗假设的无反射声波方程,可显著压制垂向附近入射的地震波背向反射;宋鹏(2005)和Zhang等(2010)改进了无反射声波方程,提升了背向反射的压制效果.然而总体而言,这类方法的背向反射压制效果尚不够理想,难以达到有效消除偏移噪声的目的.第二类是滤波方法,Mulder和Plessix(2004)直接采用高通滤波方法对成像剖面进行去噪处理,该方法易于实现但合适的滤波器阈值范围较难选取;Zhang和Sun(2009)采用Laplace滤波方法对常规逆时偏移结果进行滤波,该方法对于低波数噪声通常有很好的压制效果,但其在去噪的同时也易损失部分低波数有效信息,且会引入高频噪声(杜启振等,2013).第三类是选择性成像方法,主要包括角道集叠加压噪方法与行波分离方法.角道集叠加压噪方法需对地下每个成像点进行角道集的求取,且需选择适当的角度阈值并对小于这一角度的所有成像值进行叠加,因此该方法计算代价较高(杜启振等,2013).相比角道集叠加压噪方法,行波分离方法无需进行角道集的求取,而是直接通过修改成像条件的方式(将震源波场和检波点波场分离成不同方向的行波,然后提取有效波场分量参与成像)来压制低波数噪声,其可高效地实现地下构造的精确成像,是一种较为理想的低波数噪声压制算法.Liu等(2011)、Fei等(2015)、胡江涛和王华忠(2015)、王一博等(2016)应用Hilbert变换实现了行波分离逆时偏移成像,有效地压制了偏移噪声.Chen和He(2014)采用Poynting矢量实现了震源波场与检波点波场上、下、左、右四个方向的行波分离,其可在付出极小的计算代价的前提下有效提高低波数噪声的压制效果,因此该方法受到了专家学者们的广泛关注(王鹏飞和何兵寿,2017; 王晓毅等,2021).
然而,当前基于Poynting矢量行波分离的逆时偏移算法依然存在如下问题:首先,Poynting矢量难以精确指示波场的传播方向信息,且其计算过程容易出现不稳定的现象,因此,基于Poynting矢量分离得到的各个方向的行波并不完全精确(Du et al.,2012;Zhang,2014;Duan and Sava,2015;Li and He,2020);此外,对于行波分离后得到的多个成像剖面,诸多专家学者多是进行人为的选择性组合(Chen and He,2014;王一博等,2016;Xue and Liu,2018),且通常赋予各行波分离成像剖面一个经验权重,未能实现各个剖面的高精度叠加成像.
光流法最早应用于解决相邻帧之间物体的运动信息问题(Horn and Schunck,1981;Lucas and Kanade,1981),随后被引入到逆时偏移角道集提取中(Zhang,2014;Gong et al.,2016;吴成梁等,2021).相比于Poynting矢量,光流矢量是一个经过多次迭代运算后得到的更逼近于真实波场传播方向信息的精确矢量,且在光流矢量的计算过程中还额外加入了正则化项,这也有效避免了由于计算得到的光流矢量值为0而出现的不稳定现象.本文首先将光流矢量引入到基于行波分离的逆时偏移压噪方法中,并基于光流矢量精确稳定地实现了震源波场和检波点波场的行波分离,由此分别得到了震源波场和检波点波场的多方向行波,进而由每两个行波互相关得到16个成像剖面,在此基础上,将这16个成像剖面分别与参考剖面做相关计算,并将相关值作为权重分别赋予各成像剖面,最终实现了基于光流矢量行波分离的相关加权逆时偏移成像,显著提升了逆时偏移的成像效果.
1 逆时偏移的波场延拓计算
在二维各向同性介质中,一阶应力—速度声波方程的表达式为:
(1)
式中,x、z分别为空间坐标,vx、vz分别为质点在x和z方向的振动速度,p为应力,t为时间,ρ为密度,v为声波速度.
采用交错网格对式(1)进行有限差分离散,从而实现正向延拓和逆时延拓.以正向延拓为例,式(1)差分离散后的高阶差分格式为:
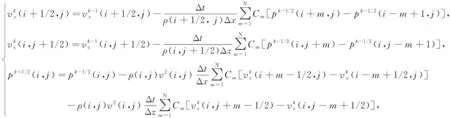
(2)
式中,k为时刻,i、j分别为x、z方向的空间离散点序号,N为差分阶数的一半,Δt为时间采样间隔,Δx、Δz为空间采样间隔,Cm为差分系数.
采用有限差分法进行波场延拓必须引入人工边界来界定计算区域,为较好地压制人工边界反射,这里采用完全匹配层(PML)方法.PML边界算法已有诸多学者进行研究(Berenger,1994;Collino and Tsogka,2001;Zhang and Shen,2010),本文在此不再赘述.
2 基于光流矢量的行波分离
Poynting矢量又叫能流密度矢量,最早应用于电磁计算领域(Poynting,1884),现在已成为地震波场计算中用于指示波场传播方向的常用算法(Yoon and Marfurt,2006).
一阶应力—速度声波方程的Poynting矢量为:
(3)
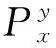
(4)
式中,Sl(x,z,t)、Sr(x,z,t)、Su(x,z,t)、Sd(x,z,t)分别为震源波场的左、右、上、下行波.由式(3)可知,Poynting矢量的计算是由波场的时间导数与空间导数的乘积组成,当时间导数或空间导数为0时,Poynting矢量值即为0,会出现不稳定的现象;此外,Zhang(2014)指出,Poynting矢量本身难以高精度地指示出波场的传播方向信息.
光流矢量是一个经过多次迭代运算后得到的,可稳定且精确地指示波场传播方向的矢量,本文将光流矢量引入逆时偏移的行波分离处理中.在二维逆时偏移中,光流问题的基本假设可以描述为邻近点的相邻时刻的波场是连续变化的,即:
u(x+dx,z+dz,t+dt)=u(x,z,t),
(5)
式中,u为波场,x、z分别为空间坐标,将u(x+dx,z+dz,t+dt)进行泰勒展开并舍去二阶以上的高阶项,可得:
uxq+uzw+ut=0,
(6)
式中,ux、uz均为波场的空间导数,ut为波场的时间导数,q和w分别为光流矢量的水平分量和垂直分量.
由于式(6)为欠定方程,需额外引入约束条件进行求解.本文引入全局平滑约束的正则化项(Horn and Schunck,1981),并构建如下的误差泛函:
E=∬[(uxq+uzw+ut)2+α2C]dxdz,
(7)

式(7)可通过梯度法进行极小化求解,可得:
(8)

(9)
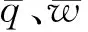
(10)
求解式(9),可得:
(11)
然后根据第n次迭代得到的光流矢量(qn,wn)可计算出第n+1次迭代的光流矢量(qn+1,wn+1),即为:
(12)
式中,n为计算光流矢量的迭代次数,其在本文模型实验中的值为10.
由式(12)可知,光流矢量不再是简单地以波场的时间导数与空间导数相乘的方式来直接求取波场传播方向信息,而是通过给定一个初始光流矢量,经过多次迭代运算后得到的一个更逼近于真实波场传播方向信息的精确矢量,且由于在光流矢量的计算过程中还额外加入了正则化项,只有当时间导数与空间导数均为0时,光流矢量值才为0,其有效避免了光流矢量计算过程中的不稳定情况.因此,从理论上来说基于光流矢量分离得到的各个方向的行波更为精确.
本文采用简单速度模型来验证基于光流矢量实现行波分离的精确性.图1为双层速度模型,第一层速度为2500 m·s-1,第二层速度为3000 m·s-1,该模型横纵向均为1500 m,空间采样间隔为5 m,震源位于(750 m,0 m)处,利用时间二阶、空间十阶交错网格有限差分进行波场延拓,震源采用主频30 Hz的雷克子波,时间采样步长为0.5 ms,记录时长为0.8 s.图2为0.3 s时刻的震源波场快照.图3a、b分别为基于Poynting矢量、光流矢量计算的反射界面附近(图2红框处)的波场方向.图4a、b分别为该时刻Poynting矢量以及光流矢量的水平分量.图5a、b分别为基于Poynting矢量、光流矢量实现波场分离后的左下行波.

图1 双层速度模型Fig.1 A two-layer velocity model
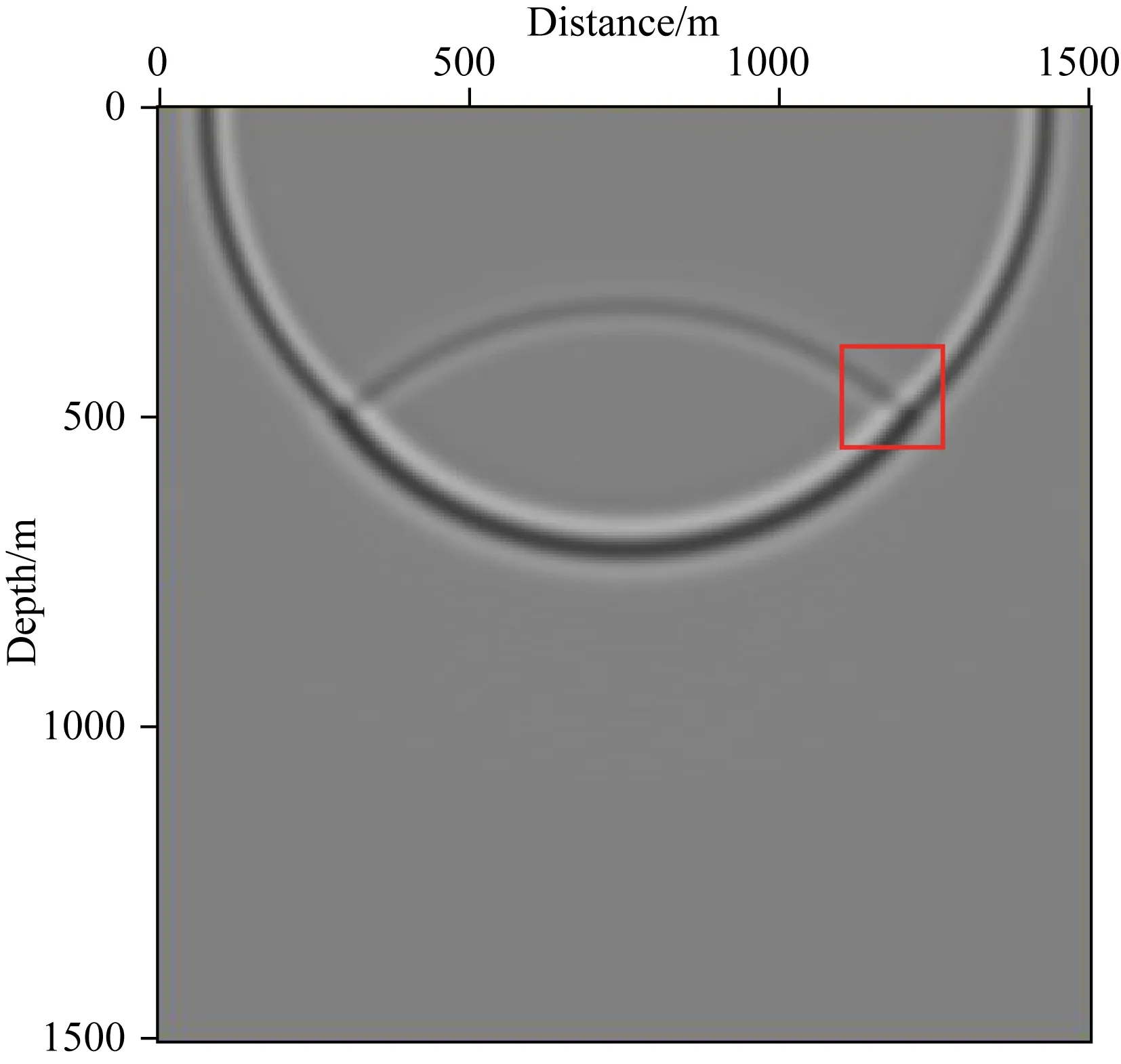
图2 0.3 s的震源波场快照Fig.2 The source wavefield snapshot at 0.3 s
由图3a、b(红圈处)与图4a、b(红色箭头处)可知,Poynting矢量难以精确指示波场的传播方向信息,且易出现奇异值,而光流矢量更为光滑,且有效避免了不稳定现象.对比图5a、b可知,基于Poynting矢量虽可实现行波分离,但由于Poynting矢量计算不精确、不稳定,其在实现过程中会引入如箭头所指处的其他行波分量,而基于光流矢量实现行波分离不会引入其他行波分量,分离得到的行波更为精确.
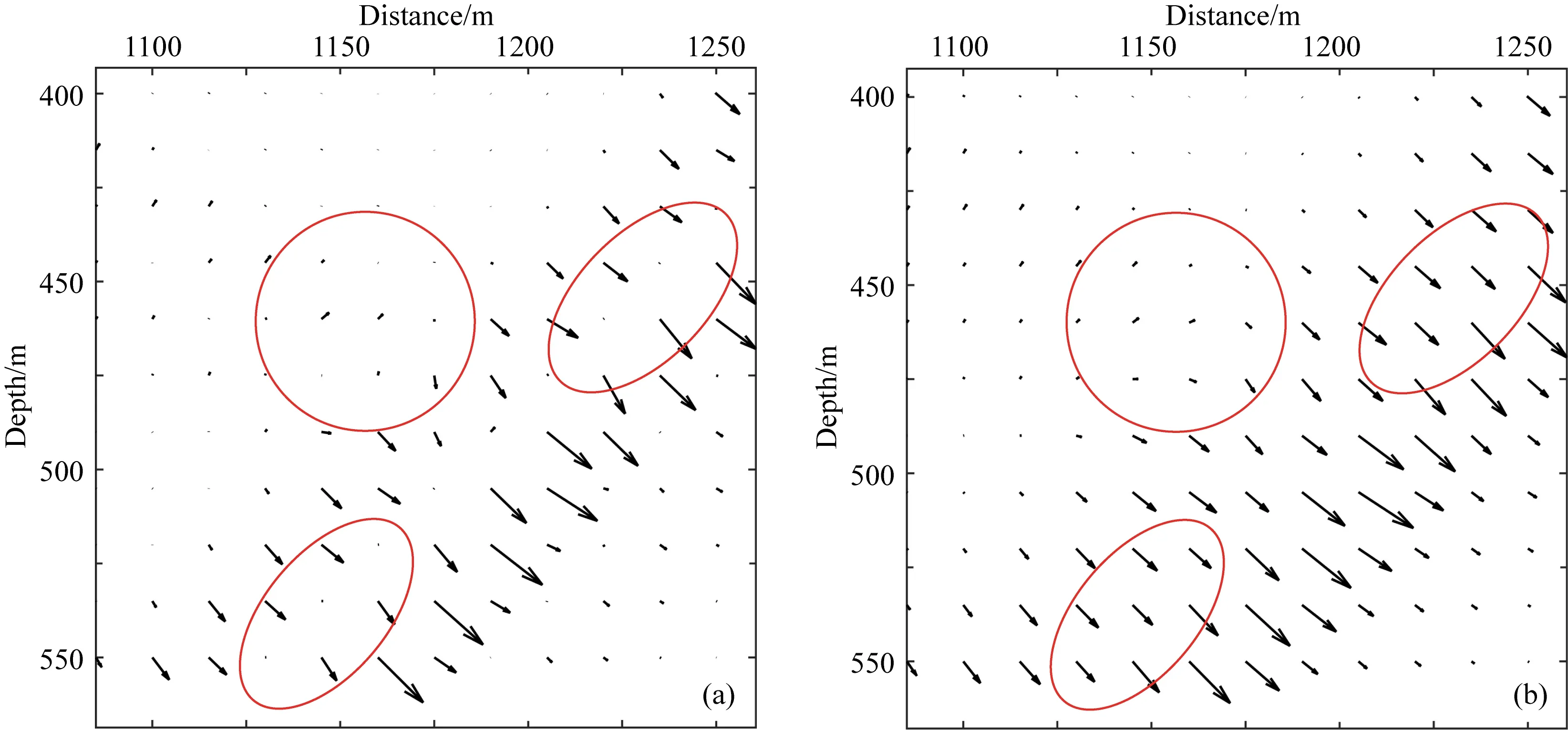
图3 波场方向(a) Poynting矢量; (b) 光流矢量.Fig.3 Wavefield direction(a) Poynting vector; (b) Optical flow vector.
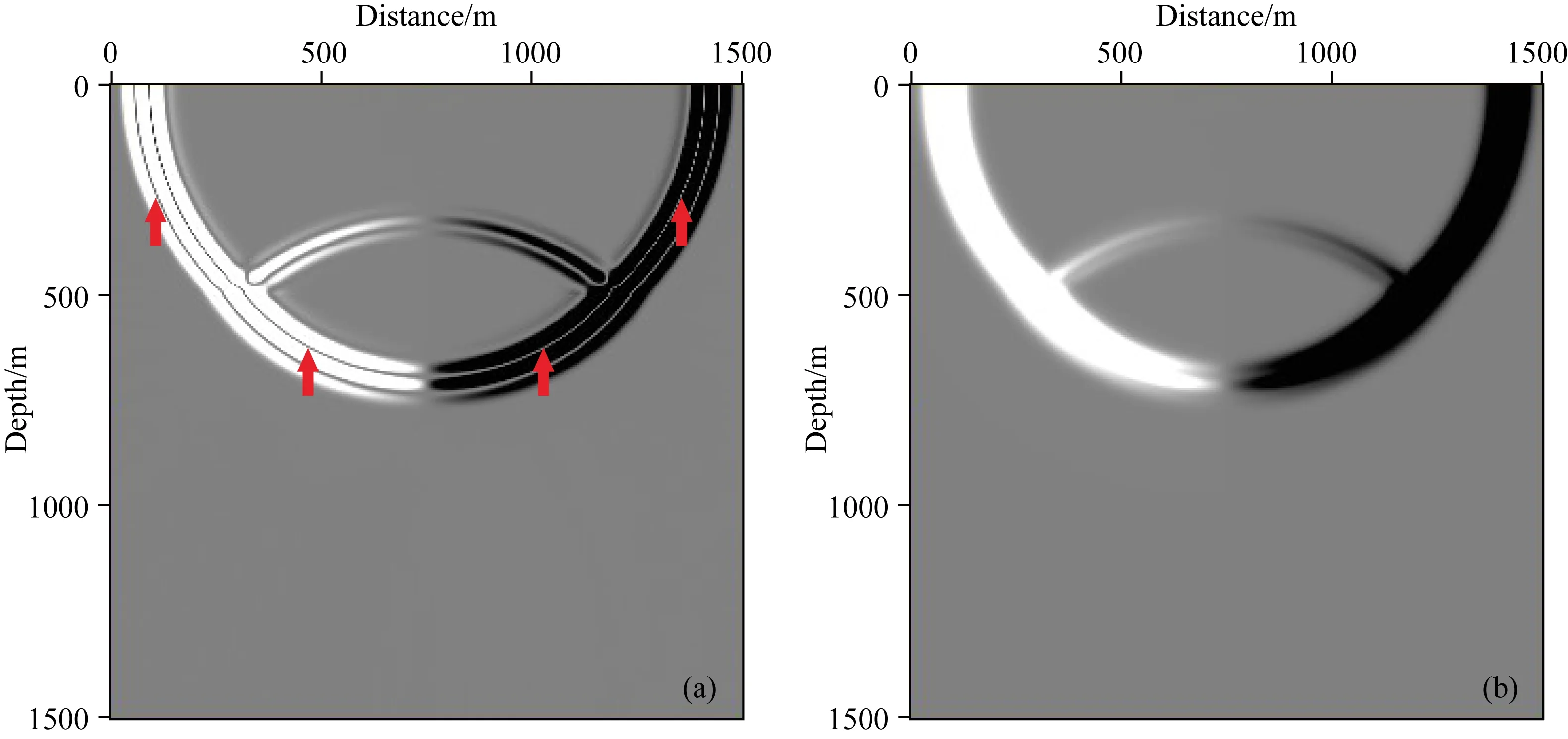
图4 水平分量(a) Poynting矢量; (b) 光流矢量.Fig.4 Horizontal component(a) Poynting vector; (b) Optical flow vector.
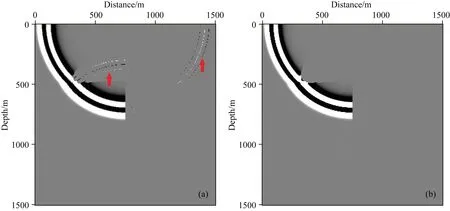
图5 波场分离后的左下行波(a) Poynting矢量; (b) 光流矢量.Fig.5 Left-down going wavefield after decomposition(a) Poynting vector; (b) Optical flow vector.
3 基于参考剖面的相关加权逆时偏移成像
本文基于光流矢量,应用式(13)实现左上、左下、右上、右下四个方向的行波分离:
(13)
式中,Slu(x,z,t)、Sld(x,z,t)、Sru(x,z,t)、Srd(x,z,t)分别为震源波场的左上、左下、右上、右下行波.Rlu(x,z,t)、Rld(x,z,t)、Rru(x,z,t)、Rrd(x,z,t)分别为检波点波场的左上、左下、右上、右下行波.根据行波分离结果,根据式(14)可进一步得到相应的16个归一化互相关成像剖面:
(14)
式中,I1(x,z)、I2(x,z),…,I16(x,z)分别为相应的16个行波分离成像剖面,分别如图6—图9所示.

图6 左上类型的震源波场与各检波点波场互相关成像结果(a) SluRld; (b) SluRlu; (c) SluRrd; (d) SluRru.Fig.6 The RTM images constructed by the cross-correlation of the left-upgoing type source wavefield with all decomposed receiver wavefields

图7 左下类型的震源波场与各检波点波场互相关成像结果(a) SldRld; (b) SldRlu; (c) SldRrd; (d) SldRru.Fig.7 The RTM images constructed by the cross-correlation of the left-downgoing type source wavefield with all decomposed receiver wavefields

图8 右上类型的震源波场与各检波点波场互相关成像结果(a) SruRld; (b) SruRlu; (c) SruRrd; (d) SruRru.Fig.8 The RTM images constructed by the cross-correlation of theright-upgoing type source wavefield with all decomposed receiver wavefields
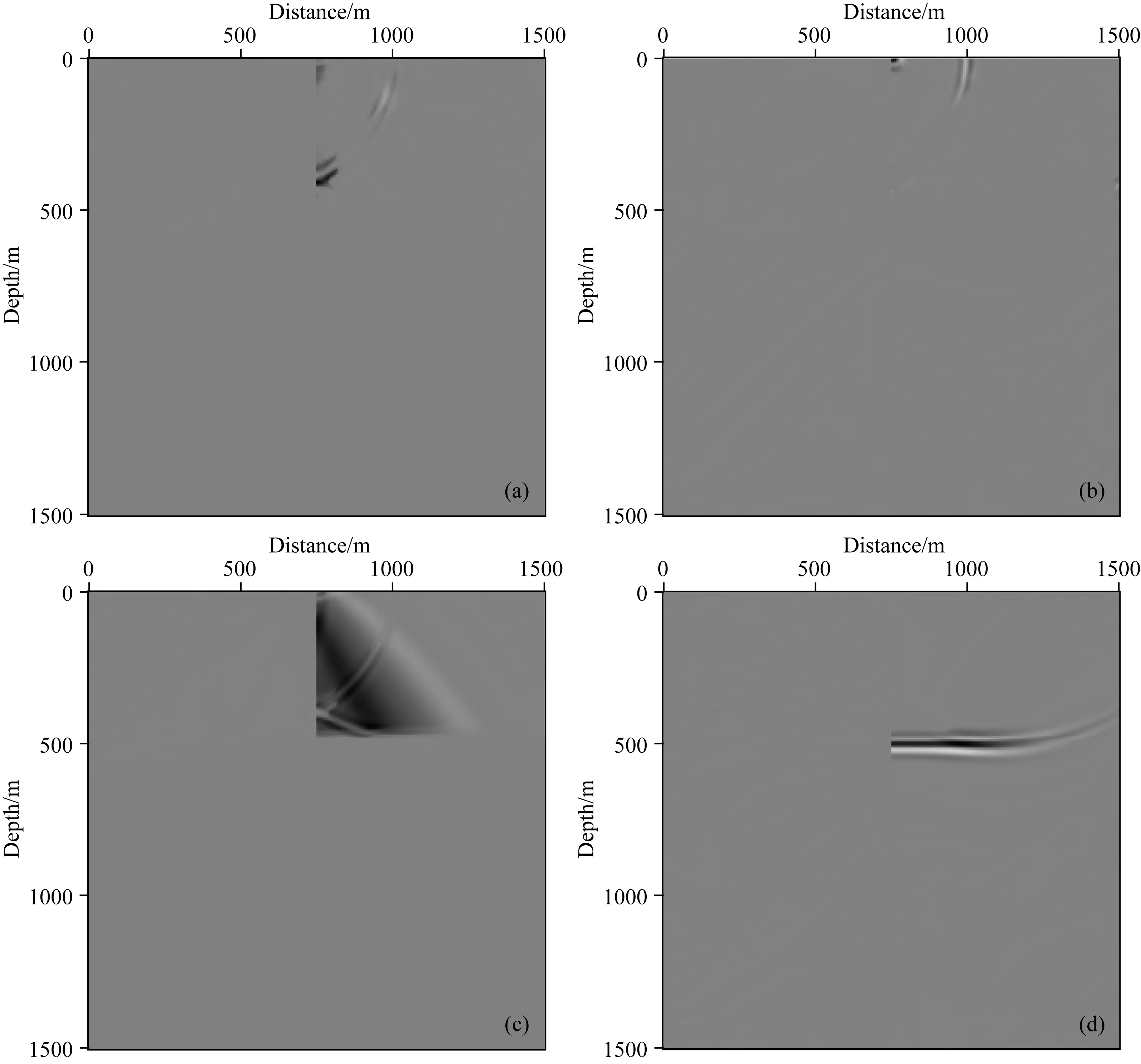
图9 右下类型的震源波场与各检波点波场互相关成像结果(a) SrdRld; (b) SrdRlu; (c) SrdRrd; (d) SrdRru.Fig.9 The RTM images constructed by the cross-correlation of the right-downgoing type source wavefield with all decomposed receiver wavefields
当前对于各个方向的正时、逆时波场相关成像结果,通常舍去同方向震源波场与检波点波场的互相关成像剖面(即I2(x,z)、I5(x,z)、I12(x,z)、I15(x,z)),并对保留的行波分离成像剖面分别赋予一个经验权重.事实上,除I2(x,z)、I5(x,z)、I12(x,z)以及I15(x,z)这四个成像剖面外,其余的剖面上依然存在低波数噪声,因此简单舍去这四个剖面的做法不能最大限度地剔除偏移噪声,且存在丢失有效信息的风险.为解决该问题,本文首先计算得到一个参考剖面Iref(x,z)(即将保留的成像剖面直接叠加),其可表示为:
Iref(x,z)=I1(x,z)+I3(x,z)+I4(x,z)
+I6(x,z)+I7(x,z)+I8(x,z)
+I9(x,z)+I10(x,z)+I11(x,z)
+I13(x,z)+I14(x,z)+I16(x,z),(15)
然后将式(14)得到的16个成像剖面分别与参考剖面做相关计算:
(16)
式中l为1至16的序号,w为各波场分离的成像剖面与参考剖面的互相关值,求取这16个互相关值中的最大值wmax,可得:
wmax=max(wl),
(17)
对互相关值w做归一化处理:
(18)
式中,W为最终的相关值,并将所得的相关值W作为权重分别赋予各波场分离的成像剖面,得到最终的基于光流矢量行波分离的相关加权逆时偏移成像结果:
(19)
这里依然采用第2节的简单速度模型来测试加权成像方法的效果.图10a为常规逆时偏移的结果,图10b为基于Poynting矢量行波分离的逆时偏移结果,图10c为基于光流矢量行波分离的逆时偏移结果.本文以图10c作为参考剖面,基于该参考剖面得到各个行波分离成像剖面的相关加权值分别为:0.0、0.0、0.0、0.0、0.0、0.99、0.01、0.002、0.0、0.0、0.0、0.0、0.013、0.002、0.0、1.0.基于光流矢量行波分离的相关加权逆时偏移结果见图10d.图10e为Laplace滤波方法逆时偏移结果.图11为相应的波数谱.
由图10、图11可知,常规逆时偏移成像结果中存在明显的低波数偏移噪声.在基于Poynting矢量行波分离的逆时偏移结果中,大部分的低波数偏移噪声得到压制,但由于行波分离不精确,其仍有部分噪声残留;在基于光流矢量行波分离的逆时偏移结果中,低波数偏移噪声得到了进一步的消除;通过对参考剖面相关加权的处理,低波数偏移噪声基本完全消除,而有效的构造成像得以凸显;从成像剖面上看,Laplace滤波方法虽然对低波数噪声的压制效果很好,但从波数谱中可以发现其处理结果中低波数信息损伤严重(如图11e中的红圈所示),存在损伤低波数有效信息的风险;此外,该方法也会引入部分的高波数噪声(如图11e中的红色箭头所示).

图10 逆时偏移的结果(a) 常规逆时偏移; (b) 基于Poynting矢量行波分离的逆时偏移; (c) 基于光流矢量行波分离的逆时偏移; (d) 基于光流矢量行波分离的相关加权逆时偏移; (e) Laplace滤波方法逆时偏移结果.Fig.10 The results of reverse time migration(a) Conventional reverse time migration; (b) Reverse time migration with wavefield decomposition based on Poynting vector; (c) Reverse time migration with wavefield decomposition based on optical flow vector; (d) Cross-correlation weighted reverse time migration with wavefield decomposition based on optical flow vector; (e) Reverse time migration using Laplace filtering.

图11 波数谱(a) 图10a对应的波数谱; (b) 图10b对应的波数谱; (c) 图10c对应的波数谱; (d) 图10d对应的波数谱; (e) 图10e对应的波数谱.Fig.11 Wavenumber spectra(a) Wavenumber spectrum corresponding to Fig.10a; (b) Wavenumber spectrum corresponding to Fig.10b; (c) Wavenumber spectrum corresponding to Fig.10c; (d) Wavenumber spectrum corresponding to Fig.10d; (e) Wavenumber spectrum corresponding to Fig.10e.
4 Marmousi模型实验
本文采用Marmousi-II局部速度模型进一步进行成像效果测试.速度模型横纵向分别为6500 m、3500 m(如图12所示),空间采样间隔为5 m.成像所用数据共101炮,从模型左端开始放炮,炮点两侧各260道接收,炮间隔为65 m,道间隔为5 m,炮点和检波点均在地表,深度为0 m.利用时间二阶、空间十阶交错网格有限差分进行波场延拓,震源采用主频30 Hz的雷克子波,时间采样步长为0.4 ms,记录时长为4 s.图13a为常规逆时偏移的结果,图13b为基于Poynting矢量行波分离的逆时偏移结果,图13c为基于光流矢量行波分离的逆时偏移结果,图13d为基于光流矢量行波分离的相关加权逆时偏移结果,图13e为Laplace滤波方法逆时偏移结果.图14为相应的波数谱.
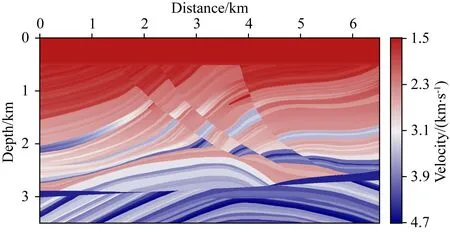
图12 Marmousi-II局部速度模型Fig.12 The local velocity model of Marmousi-II model
由图13a可知,偏移噪声严重影响了地层的成像质量,尤其在浅部地层和强波阻抗界面处,真实的成像构造被完全掩盖,成像精度较低.由图13b、c、d可知,三种行波分离方法均可起到显著的噪声压制效果,且相比常规行波分离方法,本文方法的噪声压制效果更佳,地下构造更清晰.由图13e可知,Laplace滤波方法虽可显著压制偏移噪声,然而从波数谱(图14)中可以发现,该方法在压制低波数噪声的同时极易损伤低波数有效信息(如图14e中的红圈所示),且会引入部分高波数噪声,因此从保护有效信息的角度来讲,Laplace滤波方法需谨慎使用或可作为其他成像算法的一个后续去噪处理手段.
此外,本文对Poynting矢量法和光流矢量法进行单炮逆时偏移计算效率测试,其结果如表1所示(本实验应用的GPU型号为Tesla V100).
由表1可知,本文方法的计算时间约为Poynting矢量方法的1.85倍,随着以GPU集群为代表的高性能计算机集群在地球物理领域的应用与普及,逆时偏移等成像算法通常都会有几十倍的计算效率提升,因此当前计算效率问题已不会成为限制本文算法在实际应用中的瓶颈.
5 实际资料试算
以东海某区域地震数据为例,测试本文算法的成像效果.该测线采用海洋拖揽单边放炮的采集方式,炮点位于检波点的右侧.成像所用数据共1612炮,每炮648道接收.炮间隔为37.5 m,道间隔为12.5 m,最小偏移距为187.5 m.炮点和检波点的深度为12.5 m.利用时间二阶、空间八阶交错网格有限差分进行波场延拓,时间采样步长为1 ms,记录时长为8 s.图15为该区域基于全波形反演方法得到的速度模型,横向为58.75 km,纵向为3.5 km.图16a为常规逆时偏移的结果,图16b为基于Poynting矢量行波分离的逆时偏移结果,图16c为基于光流矢量行波分离的逆时偏移结果,图16d为基于光流矢量行波分离的相关加权逆时偏移结果.

图15 实际资料的速度模型Fig.15 Velocity model of field data

图16 逆时偏移的结果(a) 常规逆时偏移; (b) 基于Poynting矢量行波分离的逆时偏移; (c) 基于光流矢量行波分离的逆时偏移; (d) 基于光流矢量行波分离的相关加权逆时偏移.Fig.16 The results of reverse time migration(a) Conventional reverse time migration; (b) Reverse time migration with wavefield decomposition based on Poynting vector; (c) Reverse time migration with wavefield decomposition based on optical flow vector; (d) Cross-correlation weighted reverse time migration with wavefield decomposition based on optical flow vector.
由图16a可知,在浅部地层处,低波数偏移噪声掩盖了真实的成像构造(如图中的黑圈所示).在图16b中,大部分的低波数偏移噪声得到压制.相比图16b,图16c中的偏移噪声更少.而在图16d中,低波数偏移噪声最少.由此可知,本文方法同样可以较好地实现实际资料的高精度成像.
6 结论与展望
本文首先基于光流矢量实现了震源波场和检波点波场的行波分离,并分别得到分离后的各方向行波及相应的16个成像剖面,在此基础上,将这16个成像剖面分别与参考剖面做相关计算,并将相关值作为权重分别赋予各成像剖面,最终实现了基于光流矢量行波分离的相关加权逆时偏移成像.理论模型数据和实际资料试算表明:
(1)光流矢量可精确、稳定地实现行波分离,基于光流矢量行波分离的逆时偏移可有效压制偏移噪声.
(2)相关加权处理避免了过多的人为干预,且可进一步压制偏移噪声、凸显有效的地下构造成像,从而显著提升逆时偏移的成像精度.
需要注意的是,与Poynting矢量相同,本文引入的光流矢量同样难以精确指示多波叠加情况下的行波传播方向.Tang和McMechan(2016)、Tang 等(2017)提出了一种多方向矢量方法,较好地实现了多行波传播方向的精确指示,但其需要付出较大的计算消耗,因此,进一步发展高效高精度的多传播方向指示算法将是下一步的主要研究工作.

