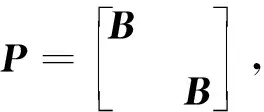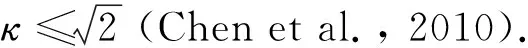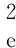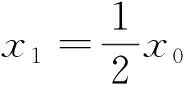基于自适应有限元正演的大地电磁法三维反演算法研究
秦策, 刘幸飞, 王绪本, 孙卫斌, 赵宁*
1 河南理工大学物理与电子信息学院, 河南焦作 454000 2 成都理工大学地球物理学院, 成都 610059 3 中国石油集团东方地球物理公司综合物化探处, 河北涿州 072750
0 引言
大地电磁法是实际工作中应用非常广泛的一种电磁勘探方法,在深部电性结构、矿产、油气和地热资源勘探等领域发挥了巨大的作用(赵国泽等, 2007).相对于一、二维反演,三维在消除假异常等方面具有很大优势(Siripunvaraporn, 2012).近年来,随着计算机硬件能力和方法理论的进步,同时三维数据采集也已逐步普及,三维反演应用越来越广泛(Dong et al., 2020; 杨文采等, 2020).反演需要使用正演来计算电磁场响应和灵敏度矩阵,三维正演是三维反演的基础,其计算精度越高,正演响应和灵敏度矩阵的精度也越高,正演计算速度越快,反演的效率也越高.在众多三维正演方法中,交错网格有限差分法有着理论简单、易于实现、计算量小等优点,是目前在三维反演中使用最多的正演方法(Siripunvaraporn et al., 2005; 胡祥云等, 2012; Kelbert et al., 2014; 董浩等, 2014; 秦策等, 2017; 阮帅等, 2020).但是,结构化六面体网格只能对地形进行近似,影响了对地形的处理效果.另外,反演中采用同套正演和反演网格,且网格不能自适应变化,这带来了反演网格设置的问题.若网格过密,则增加了反演的非唯一性;若网格过稀,则无法保证正演响应和灵敏度矩阵的计算精度,影响了反演的可靠性.在实际工作中,通常会使用不同的反演网格做多次反演,大大增加了数据处理的工作量和难度.
最近十年来,有限元法在电磁法的三维正演中得到了迅速的发展.非结构化网格(四面体和形变六面体)能够很好地模拟复杂地形和异常体.另外,自适应有限元法能够对网格进行自适应加密,相比全局网格加密可以更高效地提高正演响应的精度(Ren et al., 2013; Grayver and Bürg, 2014; 殷长春等, 2017; 赵宁等, 2019).很多学者基于有限元法实现了大地电磁法的三维反演(Grayver, 2015; Usui, 2015; Kordy et al., 2016b; Jahandari and Farquharson, 2017),也有学者将有限元法应用在了其他电磁法的三维反演中(Liu et al., 2019; Chen et al., 2020),这些研究取得了非常好的应用效果.更进一步地,若能够将自适应有限元正演方法应用在三维反演中,可以预见能够得到更好的效果.我们认为主要的困难是如何处理网格自适应加密的问题.一方面,大地电磁法的观测频率范围非常宽,因此希望能够自适应地对正演网格进行加密,不同频率使用不同的正演网格,以提高计算精度;另一方面,很多反演方法要求反演网格不能改变,反演过程中只能有一套网格,这与正演网格的自适应加密产生了矛盾.为解决此问题,我们设计了正演网格和反演网格相分离的策略,即保持反演网格不变,正演网格从反演网格出发进行自适应加密,以确保正演响应和偏导数计算的精确性,同时避免反演网格的过度参数化.
另外,有限元正演中使用的网格类型也是很多学者关心的问题.理论上,任何非结构化网格均可以模拟复杂异常体和地形.在实际应用中,由于四面体网格更容易生成,在电磁法领域应用最为广泛(Ren et al., 2013; Usui, 2015; Jahandari and Farquharson, 2017).也有一些学者利用非结构化的六面体网格得到了较好的结果(Grayver, 2015; Kordy et al., 2016a).至于哪一种网格更优,目前还没有定论.Cifuentes和Kalbag(1992)在结构问题的模拟结果中表明六面体网格的精度和稳定性相对四面体网格较高,Tadepalli等(2011)在生物力学中的模拟也得到了类似的结果,而在Ramos和Simões(2006)的股骨模拟中,四面体网格表现出了更大的优势.我们认为该问题与具体的领域相关,有待进一步研究.在本文的反演算法中,我们使用的网格分离策略需要保证加密前后的网格具有层级关系,因此选择使用非结构化六面体网格并利用八叉树方式对其进行加密.
本文的第1节介绍了三维自适应有限元正演方法,包括线性方程组的求解算法和面向目标的后验误差估计方法.第2节给出了本文中使用的L-BFGS反演算法以及网格分离策略.第3节中通过两个正演算例验证了正演算法的正确性和对地形的模拟精度,并重点对一个三维地形模型的正演数据进行了不同方法的反演,验证了本文网格分离策略的优势和处理地形问题的有效性.
1 三维正演算法
1.1 控制方程
取时谐因子为eiω t,大地电磁法中电场和磁场所满足的偏微分方程为

(1)
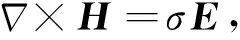
(2)
其中σ是介质的电导率,ω是角频率,μ是磁导率,其值为4π×10-7.对(1)式两边求旋度,并将(2)式带入,可得介质中电场所满足的二阶矢量亥姆霍兹方程:
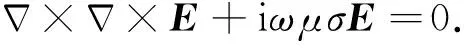
(3)
在边界上施加Dirichlet边界条件,即
n×E=n×E0,
(4)
其中n是边界网格面上的外法向向量,E0是边界上一维介质的电场响应,可以通过解析方法计算(Cagniard, 1953).
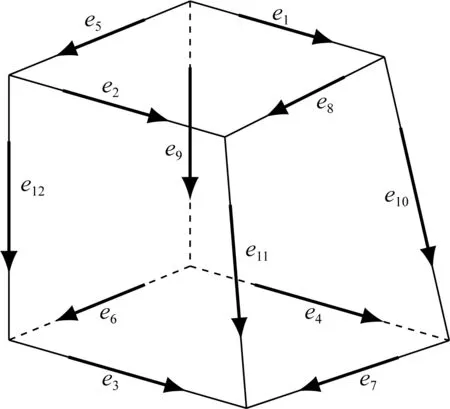
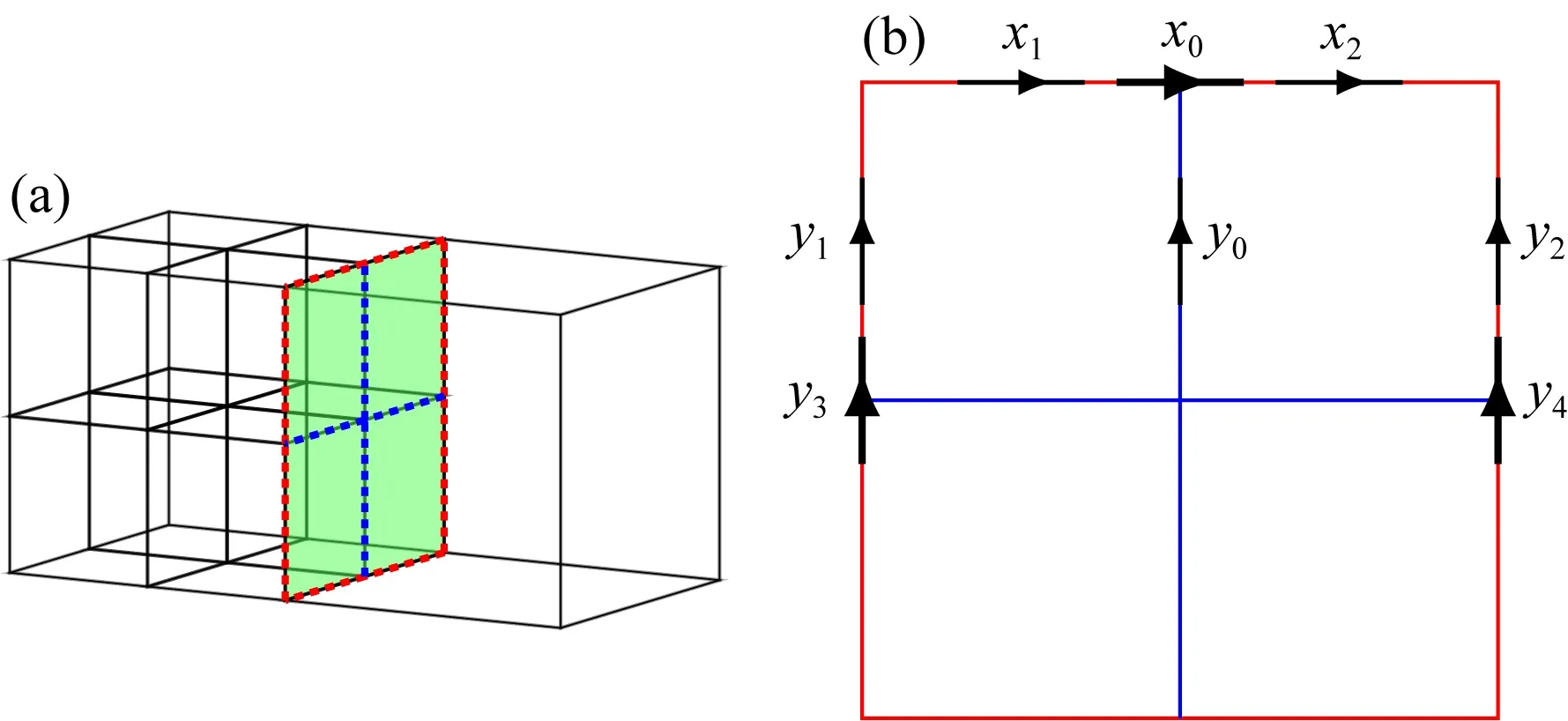
图1 非结构化六面体单元上的矢量形函数定义Fig.1 The definition of vector shape function on unstructured hexahedral element
1.2 自适应矢量有限单元法
使用数值方法求解上述偏微分方程,需要将求解区域进行离散化.为能够模拟起伏地形和复杂异常体,本文使用非结构化的六面体单元.同时,为满足电场的连续性条件,将形函数定义在单元的棱边上(Nédélec, 1986),如图1所示.在(3)式两边同时点乘矢量形函数V,并对全区域积分:
(5)
其中V∈H(curl;Ω).H(curl;Ω)是Hilbert空间上的旋度平方可积函数空间,其定义为
(6)
根据矢量恒等式和分部积分原理,式(5)可转换为
(7)
式(7)即为与式(3)所等价的泛函形式.将式(7)在区域中的每个单元进行积分并求和,可得
(8)
各单元上的积分可以由高斯数值积分方法进行计算(Venkateshan and Swaminathan, 2014).最终可得如下线性方程组
Ke=s,
(9)
任意点P处的电场值可由公式
(10)
计算.根据法拉第定律,点P处的磁场可表示为
(11)
以上两式中,ei是点P所在单元中第i个棱边上形函数的插值系数,Vi(P)是点P处第i个棱边上的形函数值.进一步可由电磁场值计算得到观测点处的阻抗张量响应.
在有限元法中,除了单元上形函数的阶数,数值解的精度基本取决于网格的大小.在三维情况下,全局网格加密会急剧地增加问题规模,是非常不经济的.本文使用基于面向目标后验误差方法的自适应网格加密来更有效地改善数值解的精度.附录B中给出了后验误差估计理论和自适应网格加密方法.
2 三维反演算法
2.1 目标函数
在反演中,我们的目标是获取一个模型,其正演响应能够在一定程度上拟合观测数据,同时又符合实际的地质规律.根据正则化反演理论(Tong et al., 2018),反演目标函数可表示为
φ(m)=(d-F)TV-1(d-F)+λmTLTLm,
(12)
上式中第一项为数据拟合项,衡量着数据拟合程度,第二项为模型约束项,λ为正则化因子,控制着模型约束项在目标函数中的比重,d为观测数据向量,m为待反演模型向量,F为模型的正演响应向量,V为数据方差矩阵,L为拉普拉斯算子的离散形式.
目前常用的反演方法大多派生自牛顿法,通过迭代法求目标函数的极小值,迭代形式为
mk+1=mk+αkpk,
(13)
其中pk为搜索方向,控制着模型的修正方向,αk为步长,控制着模型在搜索方向上的修正大小.在众多反演方法中,非线性共轭梯度法(NLCG)(Rodi and Mackie, 2001)和有限内存的BFGS方法(L-BFGS)(Byrd et al., 1994)只需计算目标函数值及其梯度,计算量较小,比较适合三维反演.其中,L-BFGS相对NLCG具有更快的收敛速度,同时确定步长所需的搜索次数也较少(秦策, 2018).经综合考虑,本文在反演中使用L-BFGS方法.
2.2 L-BFGS方法
在L-BFGS方法中,只需存储最近l次迭代中模型的修正量sk和梯度的修正量yk,其中
sk=mk+1-mk,
(14)
yk=gk+1-gk,
(15)
因此仅需要保存2l个向量,占用的内存空间较少.每一次反演迭代中,使用{s1,s2,…,sk}和{y1,y2,…,yk}近似计算Hessian矩阵,记近似Hessian矩阵的逆为Bk,搜索方向pk可表示为
pk=-Bkgk.
(16)
Bk的计算方法可参考Nocedal和Wright(2006).
在计算步长αk时,目标函数应获得足够的下降,同时计算量也不能太大.理想情况下,步长αk应是一元函数
f(αk)=φ(mk+αkpk)
(17)
的全局极小值点.但是在实际中,计算其局部极小也需要多次计算目标函数.更可行的策略是通过不精确的线搜索来获得满足条件的步长αk,既能使目标函数获得充分的下降,又花费尽量小的计算代价.最常用的条件是Wolfe条件(Nocedal and Wright, 2006),即充分下降条件
(18)
和曲率条件
(19)
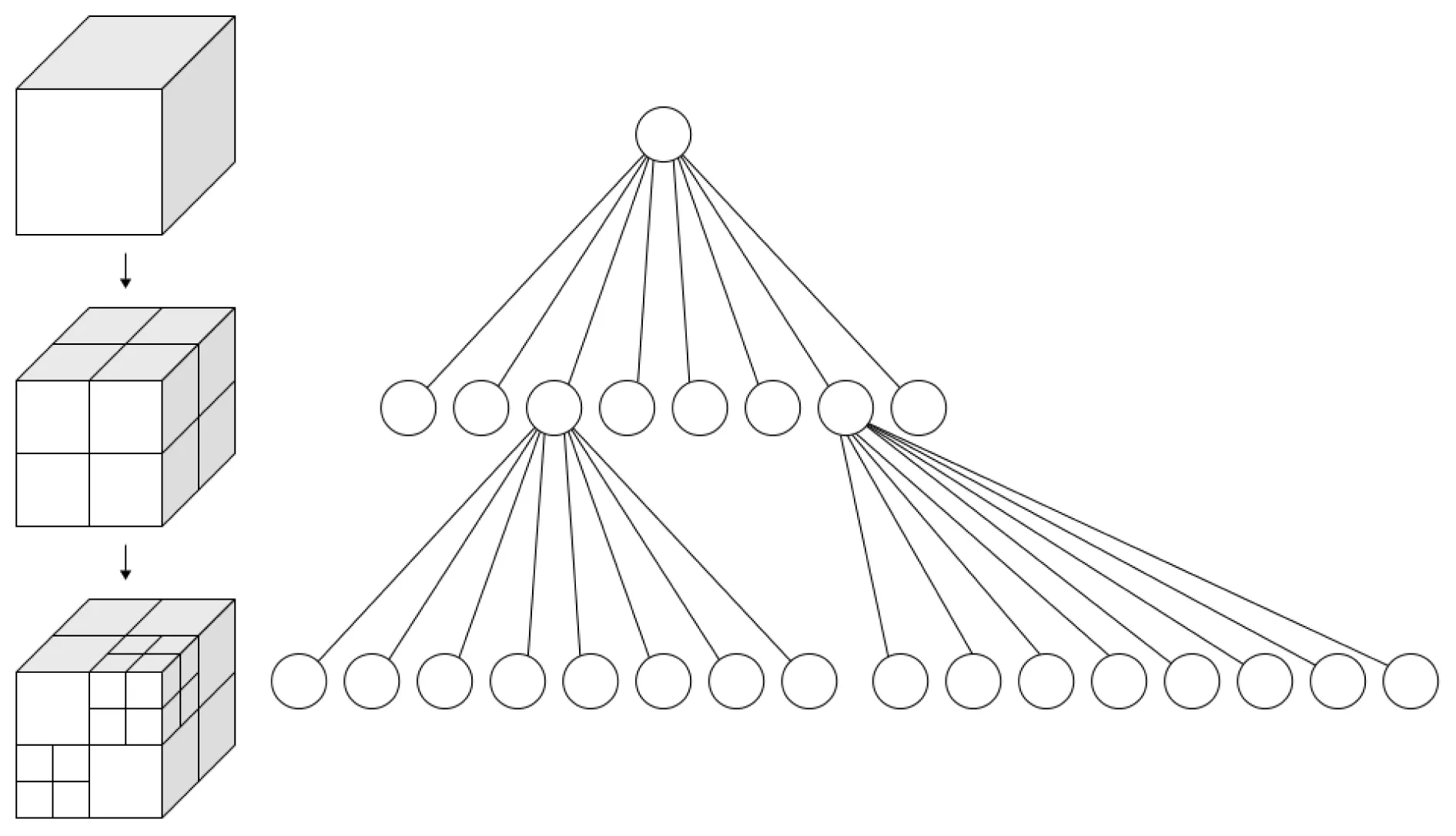
其中c1、c2为常数,且0 在自适应有限元方法中,正演网格会自适应地根据后验误差估计值进行加密,不同频率得到的最终网格也不相同.同时,L-BFGS算法也要求反演过程中网格不发生变化.为解决此问题,我们使用将正演网格与反演网格相分离的策略. 图2 网格分离策略示意图Fig.2 The schematic diagram of mesh separation strategy 算法1反演过程中梯度计算流程1:确定反演网格剖分T2:令gk=03:forf=1,…,Nfdo4: 令Tf0=T5: fori=1,…,Nmaxdo6: 对Tfi-1进行自适应加密,得到Tfi7: 令Tf=Tfi8: end for9: 在Tf上计算梯度gfk10: 令gk=gk+Dgfk11:end for 基于本文的正演和反演算法,我们使用C++程序设计语言开发了正反演程序.程序设计过程中使用了开源的有限元程序库deal.II(Bangerth et al., 2007; Arndt et al., 2021).本文的所有算例均在河南理工大学高性能计算中心的集群上完成,计算节点配备了Intel Xeon E5 2680 V4 CPU,包含14个处理器核心,主频为2.4 GHz,内存128 GB. 3.1.1 DTM1模型 为验证本文正演算法的正确性,我们使用标准模型DTM1(Dublin Test Model 1)(Miensopust et al., 2013)对程序进行测试.该模型的背景电阻率为100 Ωm,其中包含了三个电阻率差异非常大的块状异常体,异常体的位置、尺寸和电阻率如图3所示. 图3 DTM1模型示意图,图片修改自Miensopust等(2013)Fig.3 Sketch of DTM1 model, figure revised from Miensopust et al.(2013) 我们计算了10-4Hz至10 Hz范围内的21个频率的响应.正演过程中,初始网格中单元数为6498,自由度数为21640,每次加密约10%的网格,经过10次自适应加密,表1中给出了自适应加密过程中自由度的变化和计算时间.图4是全局网格加密和自适应加密过程中归一化后验误差的变化趋势,可以看到随着网格的加密,误差稳步下降.自适应网格加密时误差下降的速度更快,意味着可以用较小的计算量获得更高的计算精度.图5展示了频率分别是10 Hz和0.01 Hz时的自适应网格加密结果,可以看到网格得到了充分的加密,频率为10 Hz时浅部网格加密的较多,而频率为0.01 Hz时深部的网格更加稠密.这与我们对电磁波传播规律的认识是一致的,高频时电磁波衰减较快,因此浅部的网格加密较多;低频时电磁波衰减慢,深部的网格也需要加密.另外,由于电场穿过介质分界面是不连续的,所以网格在电阻率变化剧烈的地方加密的较多.从网格的自适应加密结果来看,本文使用的后验误差估计方法是有效的,能够较好地反映数值解的误差分布.同时,由于我们使用了面向目标的后验误差估计方法,观测点附近的网格都得到了加密,可以大幅度提高观测点处响应的精度. 表1 DTM1模型自适应加密过程中自由度数目及计算时间Table 1 Number of DoFs and computational time for DTM1 model using adaptive mesh refinement 图4 DTM1模型10 Hz和0.01 Hz自适应网格加密归一化误差收敛速度Fig.4 Normalized estimated errors using adaptive mesh refinement for the DTM1 model for frequency 10 Hz and 0.01 Hz 图5 DTM1模型第10次自适应加密结果(a)10 Hz;(b)0.01 Hz.Fig.5 Adaptive mesh refinement result of DTM1 model 已有很多学者对此模型进行了模拟(Miensopust et al., 2013).(0 km,0 km)位于三个异常体交界处的上方,其响应最为奇异.图6中展示了本文的计算结果与Mackie等(1993)的有限差分结果、Nam等(2007)等的有限元结果的对比.从图中可以看出,Zxy和Zyx的视电阻率和相位响应吻合良好,这证明了本文所采用方法的正确性. 图6 DTM1模型(0 km, 0 km)处的响应Fig.6 The response of DTM1 model at (0 km, 0 km) 3.1.2 地形模型 非结构化网格的优势之一是可以精确地模拟起伏地形.一般来说,四面体单元的适应性最强,可以模拟任意复杂的地形.在本文中,我们使用非结构化六面体单元,通过对单元进行形变也可模拟起伏地形.通过对一个二维山脊地形(Wannamaker et al., 1986)进行模拟来验证程序对地形处理的正确性.该模型的背景电阻率为100 Ωm,模型的中间位置包含一平台状的地形,如图7所示.计算了频率为2 Hz时的响应.图8中展示了初始网格和经过5次自适应加密得到的最终网格.初始网格非常稀疏,最终网格中,网格得到了充分加密.与DTM1模型类似,测点附近网格的加密次数更多,解的精度得到了保证. 图7 二维山脊地形模型示意图Fig.7 The diagram of 2D ridge topography model 图8 二维山脊地形模型网格自适应加密结果(a) 初始网格; (b) 最终网格.Fig.8 Adaptive mesh refinement result of 2D ridge topography model(a) Initial mesh; (b) Final mesh. 使用开源的二维自适应有限元正演程序MARE2DEM(Key, 2016)对此模型进行了模拟,并和我们的计算结果进行对比,如图9所示.可以看到,两者吻合良好,这验证了我们使用的非结构化六面体网格在处理地形问题时的正确性.另外,从响应中也可发现,地形的影响非常大.因此,在地形起伏情况下,其影响是不能忽略的,必须加以处理,否则会对反演结果产生严重的干扰.我们将在反演算例部分对地形的处理方法进行讨论. 图9 二维山脊地形模型响应(频率为2 Hz)Fig.9 Response of 2D ridge topography model (frequency is 2 Hz) 3.2.1 简单三维模型 我们首先通过对一个简单模型进行反演来验证算法的效率.此模型的背景电阻率为100 Ωm,其中包含4个块状异常体(2个高阻异常体和2个低阻异常体),电阻率分别为10 Ωm和1000 Ωm,异常体的尺寸为10 km×10 km×5 km,相邻异常体的间距为5 km,异常体的埋深为2.5 km,如图10所示. 图10 简单三维模型示意图Fig.10 The diagram of simple 3D model 计算了21个频率(对数等间隔地分布在10-3~10 Hz范围内)的阻抗张量响应,并在数据中加入2%的高斯噪声,对数据进行了反演.初始数据拟合差为16.7,经过18次迭代下降至0.97,反演结果如图11所示.从图中可以看到,四个块状异常体的电阻率和形态都被反演出来,且与真实模型吻合良好.验证了本文反演算法的收敛速度和反演程序的正确性. 图11 简单三维模型反演结果Fig.11 Inversion result of simple 3D model 3.2.2 三维地形模型 在前文的正演地形算例中,我们看到,大地电磁响应受地形影响非常严重,因此在处理实测数据时,必须对地形进行处理.一些学者提出了地形校正的方法(Nam et al., 2008),即根据地形的响应特征,将地形的干扰从观测数据中分离出去,再对不包含地形影响的数据进行反演.另外一种思路是不对数据进行任何处理,将地形包含在初始模型中进行反演.已有研究表明,即使使用台阶状的网格近似地形,也可以提高对地形的模拟精度,一定程度上减弱地形对反演结果的影响 (董浩等, 2014; 余辉等, 2019; 顾观文和李桐林, 2020). 我们建立了如图12所示的地形模型,通过对该地形模型的正演合成数据进行反演来讨论地形数据的处理方法.模型的背景电阻率为100 Ωm,包含2个块状异常体,电阻率分别为10 Ωm和1000 Ωm,尺寸为10 km×10 km×5 km.两个块状异常体上方各有一个平台状的正地形,高度为2 km.观测区域范围为22.5 km×37.5 km,覆盖了整个地形区域,测点间距2.5 km,如图12b中十字符号所示.观测频率共21个,对数等间隔地分布在10-3Hz至10 Hz范围内. 图12 三维地形模型示意图Fig.12 The diagram of 3D topography model 使用本文的自适应正演方法对此模型进行计算,并在阻抗张量响应中加入了2%的高斯噪声,得到地形模型的合成数据.我们首先使用近年来在学术界应用比较广泛的三维反演程序ModEM(Kelbert et al., 2014)对此数据进行反演.ModEM使用的是交错网格,对地形的近似程度取决于地形附近网格单元的大小,因此我们使用了三种不同尺度的网格.在地形区域,纵向的网格单元尺寸设置为100 m,横向网格单元尺寸分别选择500 m、1000 m和2500 m.如图13所示,三种尺度的网格都能在一定程度上对地形进行模拟,单元尺寸越小,对地形的近似程度越高,但同时也会导致区域内网格数目急剧增长.图14展示了使用不同尺寸网格的反演结果,图15是反演过程中RMS的收敛过程.可以看到,单元尺寸为2500 m时的反演结果很好地恢复了低阻和高阻异常体,但是背景中有虚假异常.经过50次迭代RMS只下降到约2.7,这是由于对地形的近似比较粗糙,不能很好地拟合数据.单元尺寸为1000 m和500 m时对地形的近似比较好,经过约30次迭代数据即得到了很好的拟合,低阻异常体的位置和电阻率都得到了较好的反映.但是,在结果中几乎看不到高阻异常体.我们推测主要有两方面的原因,一方面由于大地电磁法本身对高阻体不灵敏,另一方面可能是因为反演参数过多增大了反演的非唯一性. 图13 三维地形模型交错网格剖分示意图(a) 水平网格尺寸500 m; (b) 水平网格尺寸1000 m; (c) 水平网格尺寸2500 m.Fig.13 Staggered grids of 3D topography model(a) Cell size 500 m; (b) Cell size 1000 m; (c) Cell size 2500 m. 图14 三维地形模型交错网格反演结果Fig.14 Inversion results of 3D topography model using staggered grids 图15 三维地形模型交错网格反演过程RMS收敛曲线Fig.15 Convergence curve of RMS in the inversion process of 3D topography model using staggered grids 上述反演结果表明,使用较粗的网格很难拟合数据,而网格较密时反演非唯一性过强,反演结果并不理想.我们进一步使用本文的方法对地形数据进行反演,目标区域的网格单元尺寸为2500 m,并对地表附近的网格进行了加密和形变以适应地形.反演初始模型为100 Ωm的均匀半空间,同时我们也进行了不包含地形的反演.反演结果如图16所示. 图16 三维地形模型反演结果(a) 真实模型; (b) 包含地形的反演结果; (c) 不包含地形的反演结果.Fig.16 Inversion result of 3D topography model(a) The true model; (b) The inversion result with topography; (c) The inversion result without topography. 可以看到,在包含地形的反演中,两个异常体的尺寸、位置和电阻率都得到了较好的反映,模型背景也较为干净.相对地,在不包含地形时,反演结果较差,高阻体基本没有反演出来,反演结果中也出现了许多虚假异常.另外,低阻体的形状不准确,且位置发生了下移.我们认为主要的原因是正地形产生的低电阻率异常掩盖了高阻体的响应,导致高阻体未反演出来,同时也增强了低阻体的响应,导致其位置下移. 图17展示了两种情况下数据拟合差随迭代次数的变化趋势,在包含地形的情况下,经过23次迭代数据拟合差由10.3下降至0.98,而在不包含地形的情况下,经过50次迭代数据拟合差由20.5下降至2.3,且在后20次迭代中几乎没有下降,可以预见继续迭代下去也不会进一步下降.这说明在不包含地形的情况下,很难寻找到一个模型能够拟合地形数据,反演过程陷入局部极小.反演结果中的虚假异常体可能是迭代过程中为强行拟合地形数据所产生的“噪声”. 图17 三维地形模型反演过程RMS收敛曲线Fig.17 Convergence curve of RMS in the inversion process of 3D topography model 在反演初始模型中,我们使用了较为稀疏的网格.在计算梯度过程中,正演网格由反演网格出发自适应加密5次,每次加密约10%的网格.图18展示了反演网格和频率为0.1 Hz和10 Hz时包含地形的反演过程中最后一次迭代的正演网格.反演网格中单元数目为14400,经过加密,单元数目分别为442954和500375.从图中可以看到,两个频率的正演网格都得到了充分的加密,且10 Hz的正演网格浅部加密的较多,而0.1 Hz的正演网格深部加密的较多,与前文中DTM1模型的结果是一致的.这也说明了网格分离策略的优势,不同频率的正演使用不同的网格,从而保证所有频率的计算精度. 图18 包含地形的反演过程最后一次迭代中的正演网格(a) 反演网格; (b) 0.1 Hz时的正演网格; (c) 10 Hz时的正演网格.Fig.18 The forward mesh in the last iteration of the inversion process with topography(a) Inversion mesh; (b) Forward mesh of 0.1 Hz; (c) Forward mesh of 10 Hz. 本文基于自适应有限元算法,实现了大地电磁法的三维正演程序,并通过网格分离策略将其应用到了的大地电磁法的三维反演中.在正演中,我们使用了非结构化六面体网格和面向目标的后验误差估计方法,计算精度较高且能够模拟起伏地形,两个正演算例验证了处理复杂模型和地形的有效性.反演中,通过使用两套网格,将反演网格和正演网格分离.加密的正演网格保证了正演响应和灵敏度的计算精度,保证了反演的可靠性,同时较为稀疏的反演网格也不会增多反演参数个数.最后通过对三维地形模型的反演讨论了地形数据的处理方法.本文的方法具有一定的通用性,也可用于其他电磁法的三维反演中. 本文还有很多需要改进的地方.首先,在反演过程中,我们没有进行反演网格的加密.主要有两方面的原因,一方面,我们使用的L-BFGS方法要求反演过程中反演参数个数不能变化,否则会破坏反演过程中存储的辅助信息的一致性;另一方面,对于实测数据,我们并不知道需要在哪些位置加密反演网格以提高分辨率.Grayver(2015)使用模型的空间导数来加密反演网格,在合成数据的反演中显示了良好的效果,可以提高反演结果中特定位置的分辨率,但目前尚不清楚该方法是否适用于复杂的实测数据.另外,本文只对理论模型进行了试算,还未对实测数据进行测试.后续将针对这两方面进一步开展研究工作. 致谢本文的研究过程中使用了河南理工大学高性能计算中心的计算设备,特此表示感谢.也感谢审稿专家百忙之中审阅我们的论文并提出宝贵建议. 附录A 复系数线性方程组求解算法 令K=Kr+iKi,e=er+iei,s=sr+isi,式(9)可改写为 (A1) 为了保证其对称性,将上式中的第二行两端同时乘以-1,可得 (A2) 式(A2)中矩阵阶数为式(9)中矩阵阶数的2倍,与式(9)完全等价.为方便起见,我们将式(A2)中的系数矩阵记为A.构造分块对角矩阵: (A3) Py=c, (A4) 其中c是任意向量.由于P具有分块对角特性,上式可以转换为求解两次如下方程: Bz=d. (A5) 我们使用共轭梯度法来求解式(A5),并使用辅助空间算法作为预条件(Hiptmair and Xu, 2007). 附录B 面向目标后验误差估计方法 记有限元解为E,单元上的后验误差可表示为 (B1) (B2) (B3) 其中,he和hf分别是单元e的外接球和面f的外接圆的直径,nf表示面上的外法向向量,[·]表示相邻单元交界面处的跳跃量. 给定有限元解E,计算式(B2)需要在每个单元上对偏微分方程的残差进行积分.计算式(B3)中的跳跃量需要对[·]中的式子分别在相邻的两个单元交界面上进行积分,再计算其差值.上述积分可使用高斯数值积分方法来计算,即在每个单元上的8个积分点处计算待积分函数值,再乘以权重并求和(Venkateshan and Swaminathan, 2014). 在大地电磁法中,通常主要关心观测点所在位置解的精度.我们使用面向目标的自适应加密策略来针对性地提高测点处解的精度(Ren et al., 2013; 殷长春等, 2017).即通过在观测点处放置一个点源来构造对偶问题,使用对偶问题解的后验误差估计值对原后验误差估计值进行加权.由于点源的奇异性很强,所以它的后验误差估计值能够有效地区分对观测点处精度影响较大的单元,使用加权后的误差估计值指导网格加密可以快速提高观测点处解的精度.记对偶问题的解为ED,则面向目标的后验误差估计值可表示为 ηgo=ηe(E)ηe(ED). (B4) 由式(B4)得到的后验误差估计值可以指导正演计算过程中的局部网格加密.对于六面体网格,通常使用八叉树的方式对其进行加密,即把一个六面体单元的每条边都一分为二,连接各边中点、面中心点和单元中心点,可得到八个单元,如附图B1所示. 附图 B1八叉树局部网格加密示意图Appendix Fig.B1 The schematic diagram of octree local mesh refinement 附图B2 非协调网格示意图(a) 由相邻网格加密次数不同产生的非协调网格; (b) (a) 中左侧4个网格与右侧网格相交界面.Appendix Fig.B2 The schematic diagram of non-conforming mesh(a) Non-conforming mesh generated by different refinements of adjacent cells; (b) Intersection of 4 left cells and right cell. 需要注意的是,若相邻单元的加密次数不同,则会产生悬挂点.如附图B2a所示,细网格中红色棱边与相邻粗网格中较长的棱边部分重合,蓝色棱边与相邻粗网格的面相交,破坏了有限元解的切向连续性,须对其施加约束.附图B2b是附图B2a中网格交界面的平面图,与自由度x1、x2关联的棱边的长度是与x0关联的棱边的长度的一半,它们之间应满足的条件为 (B5) 与自由度y0关联的蓝色棱边与相邻单元的面相交,y0应等于与其同方向的两个自由度(y1、y2)的平均值,即 (B6)2.3 网格分离策略

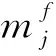


3 数值算例
3.1 正演算例
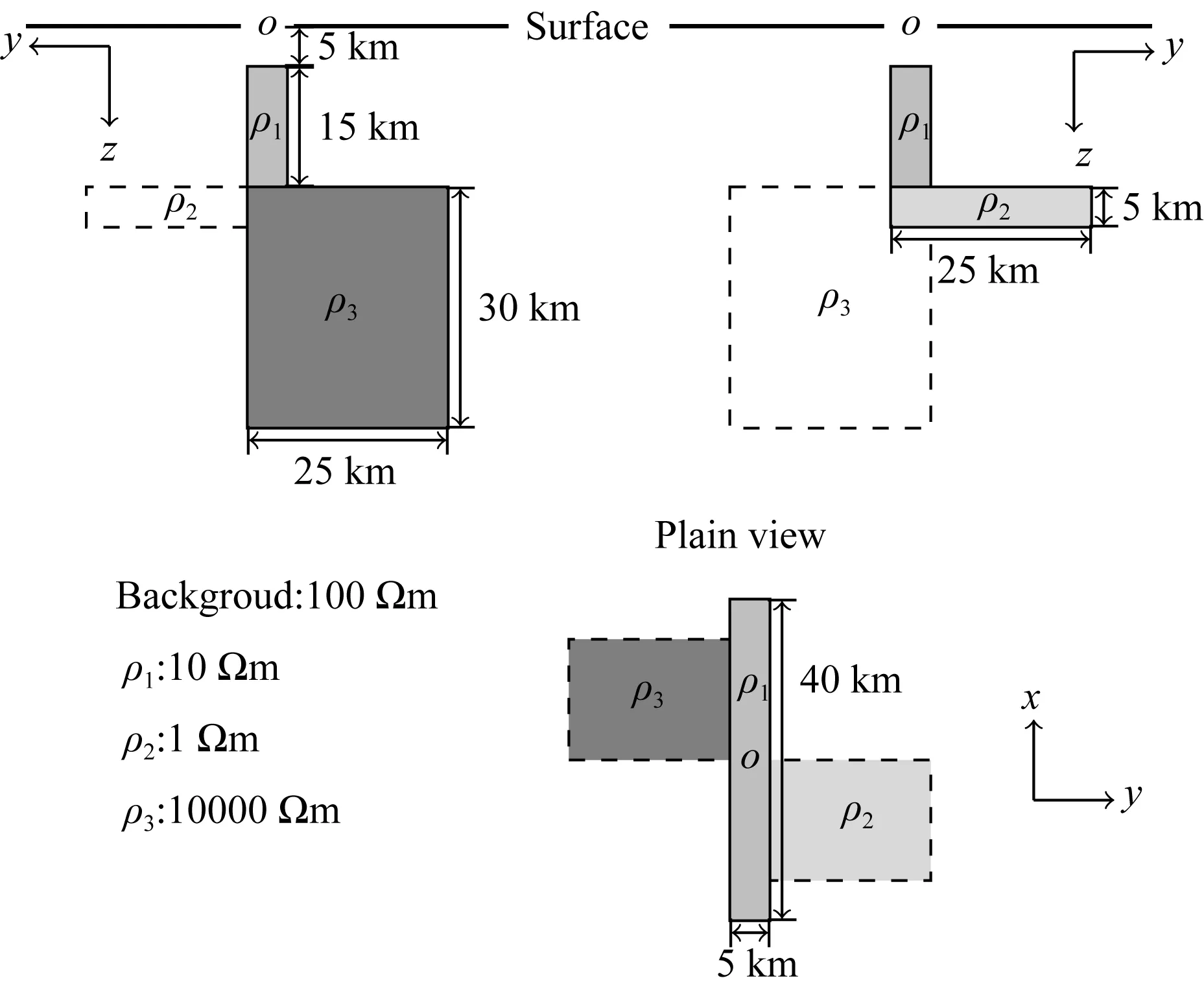
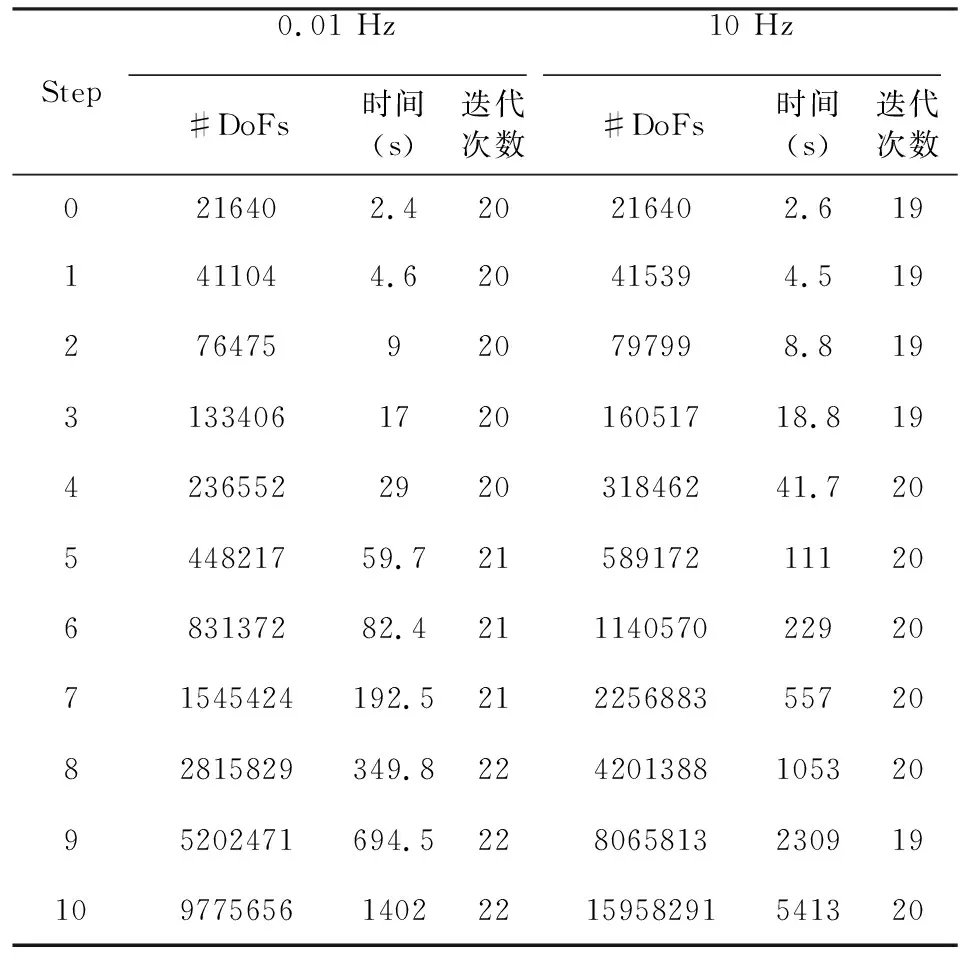
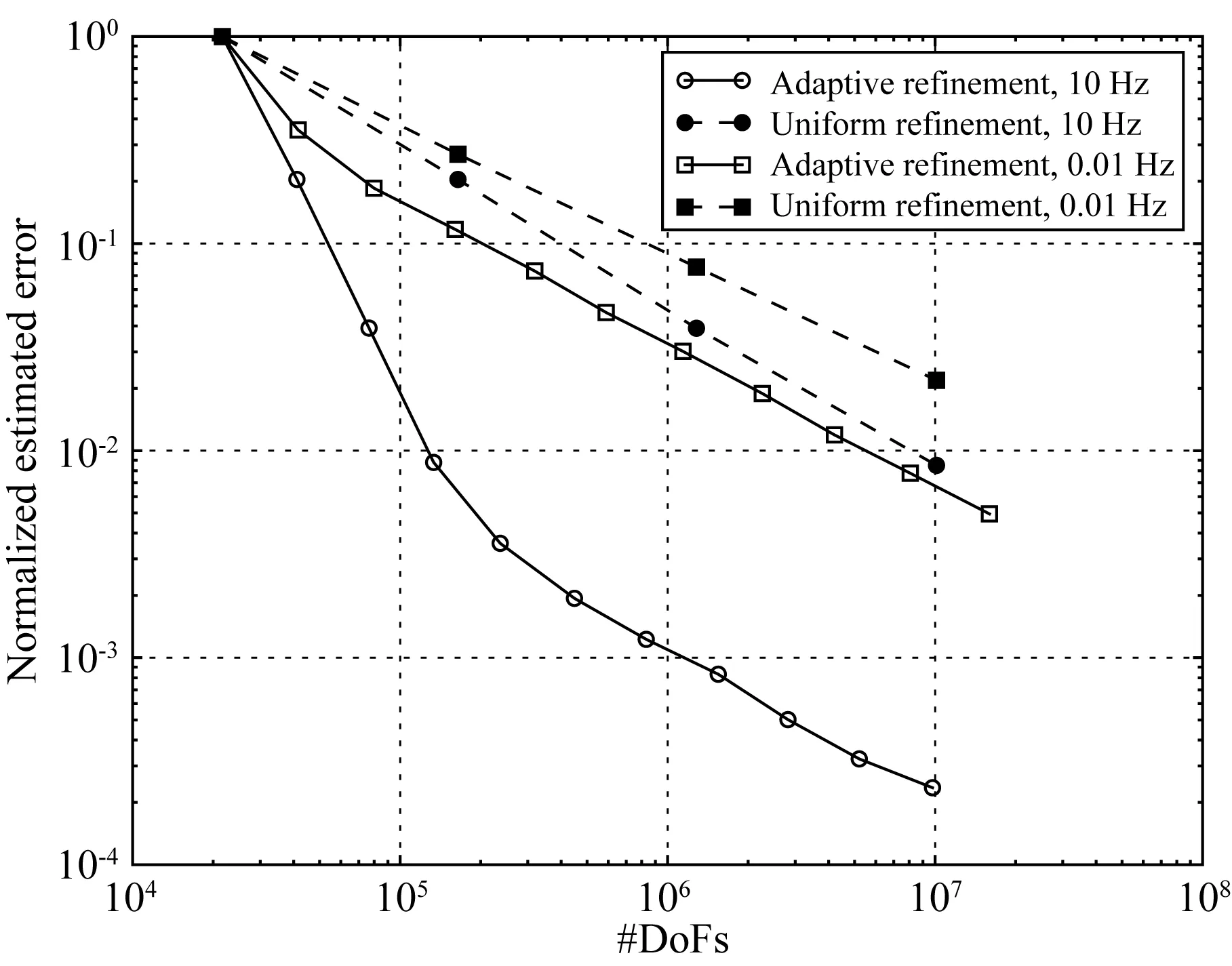
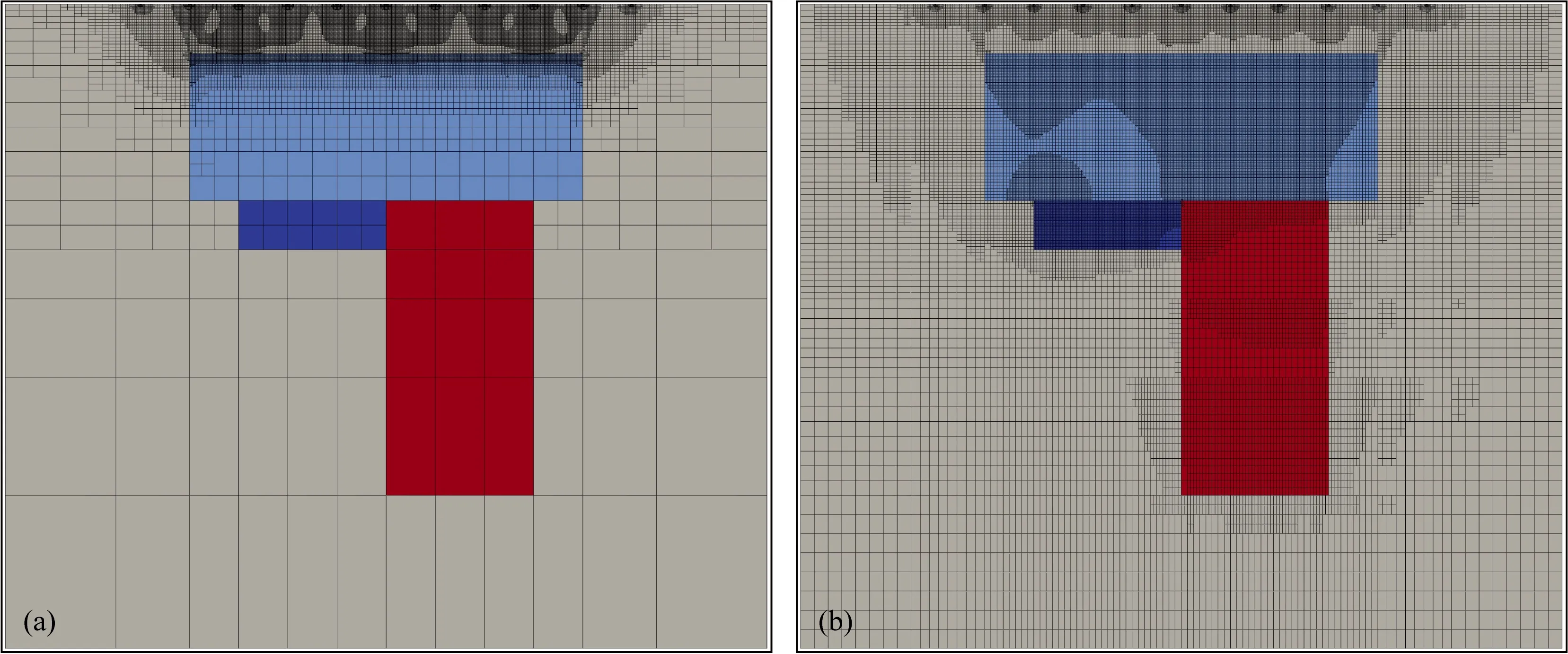
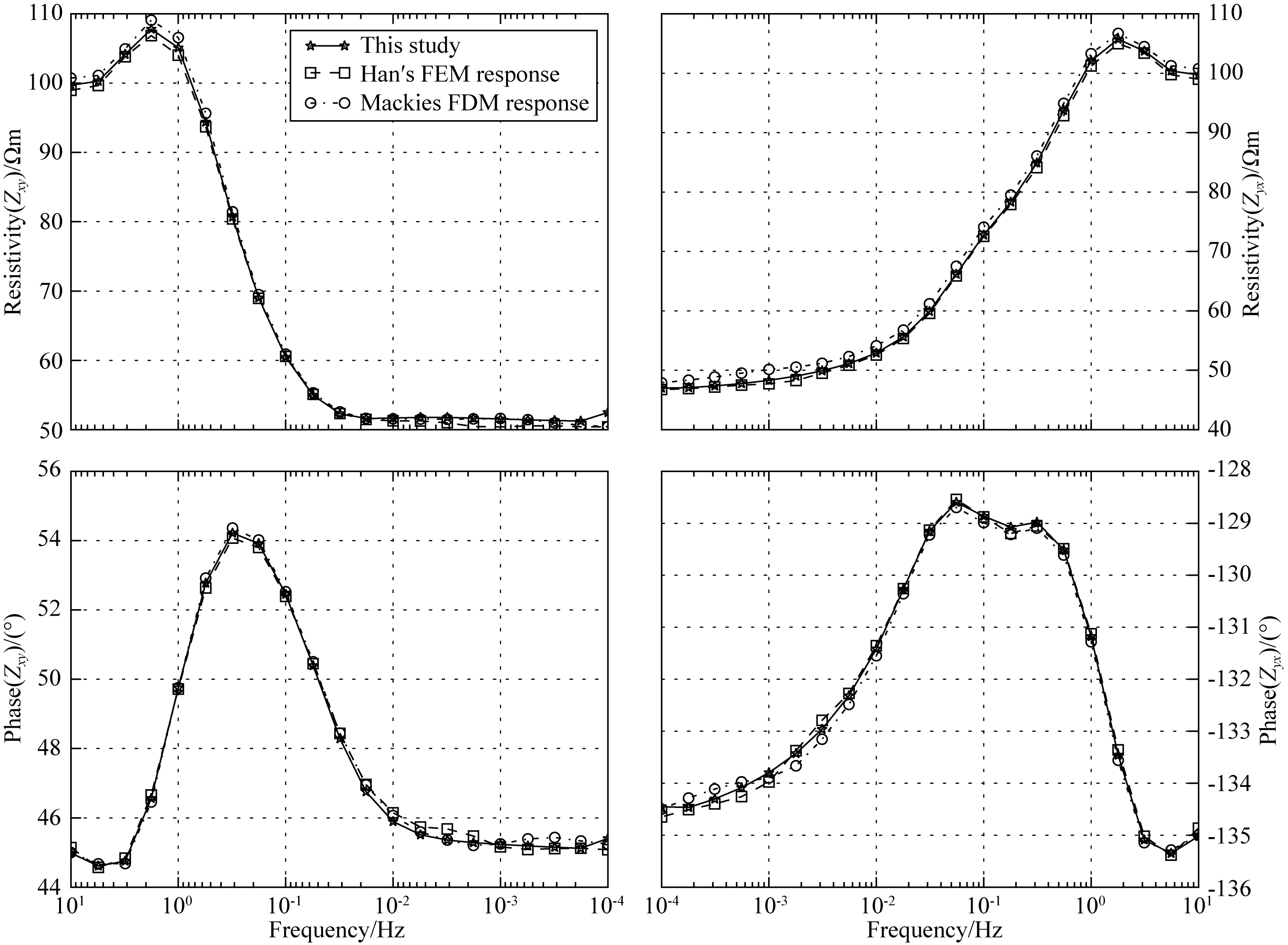
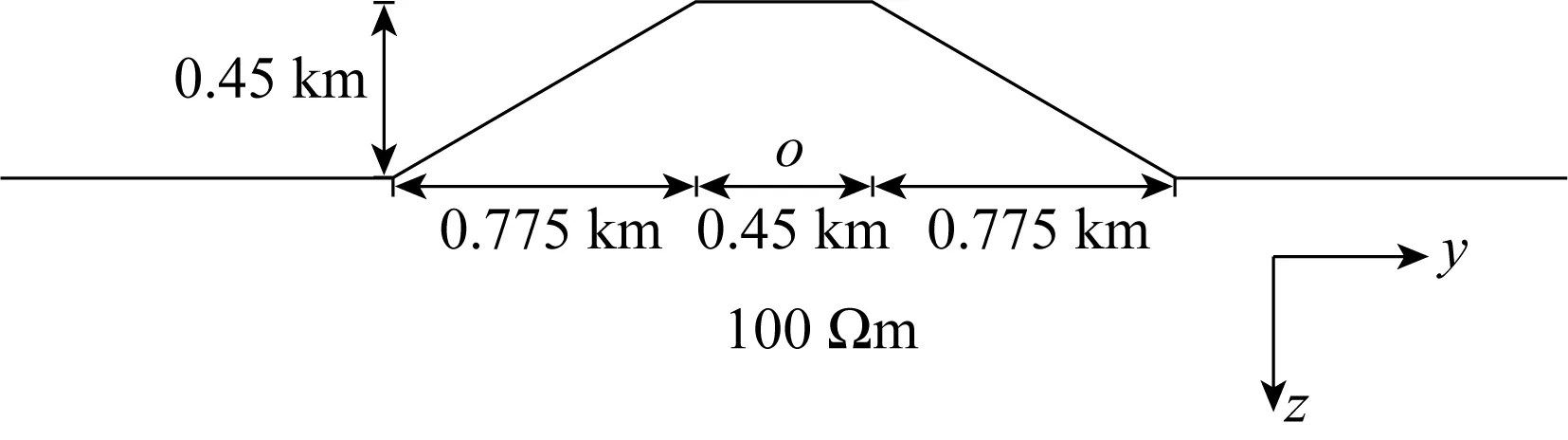
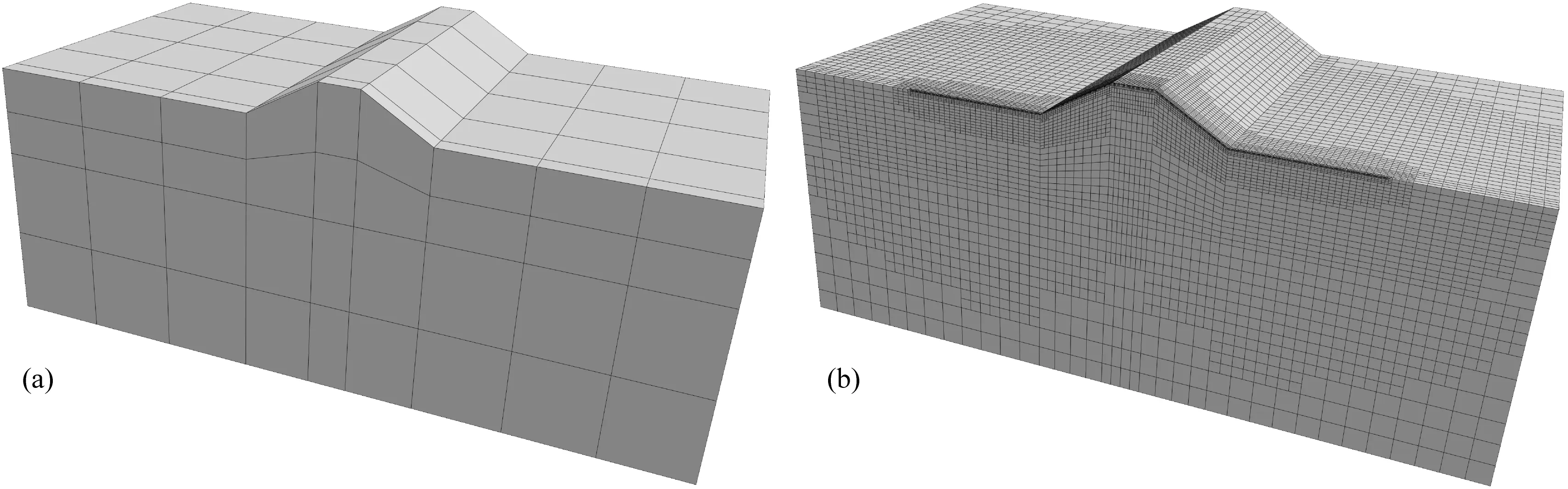
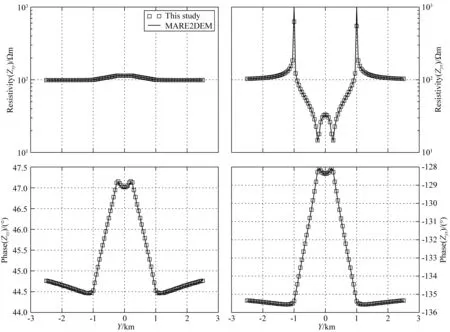
3.2 反演算例

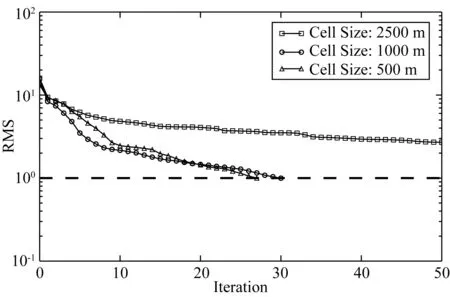
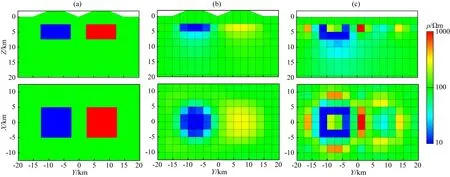
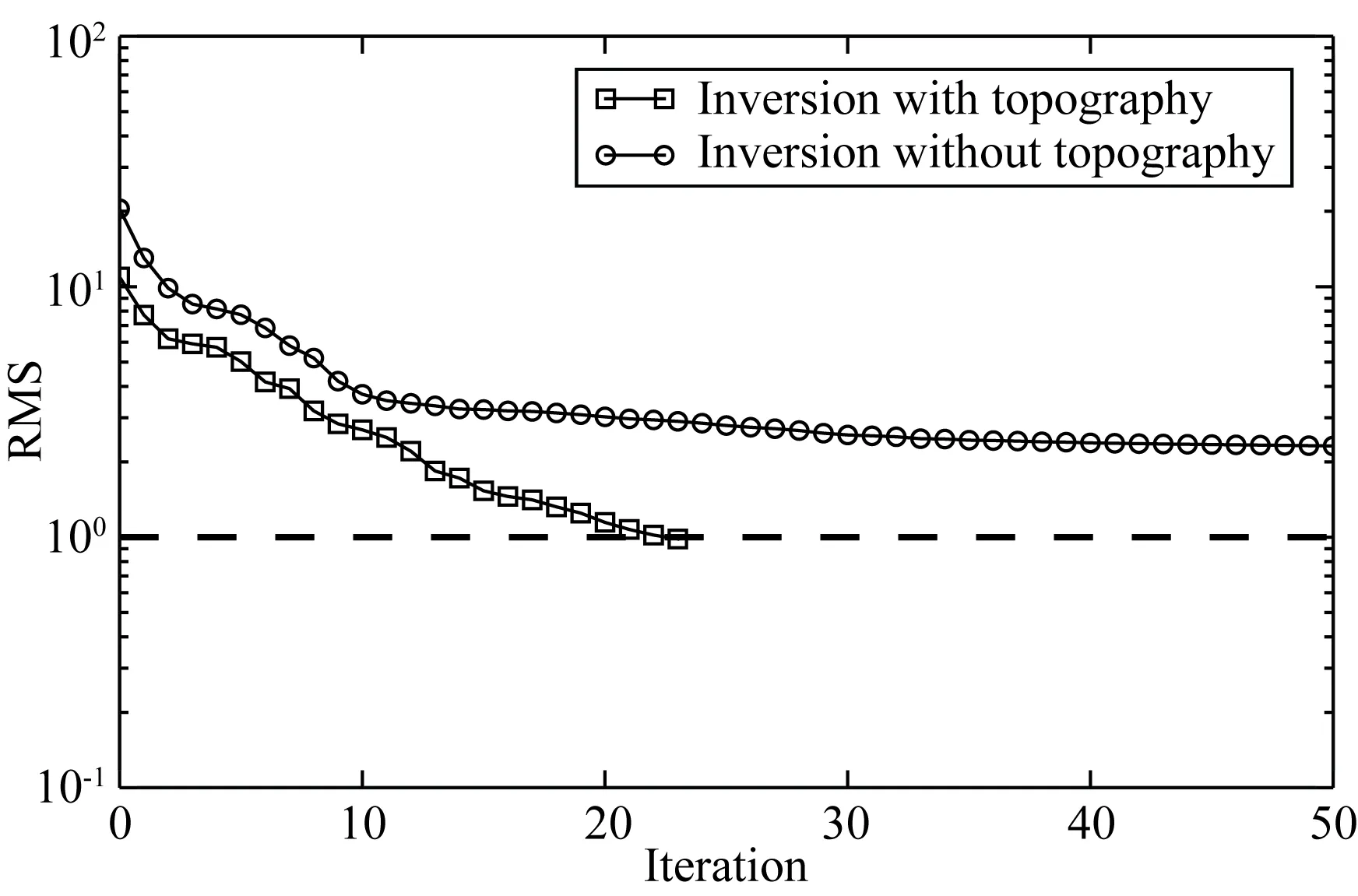
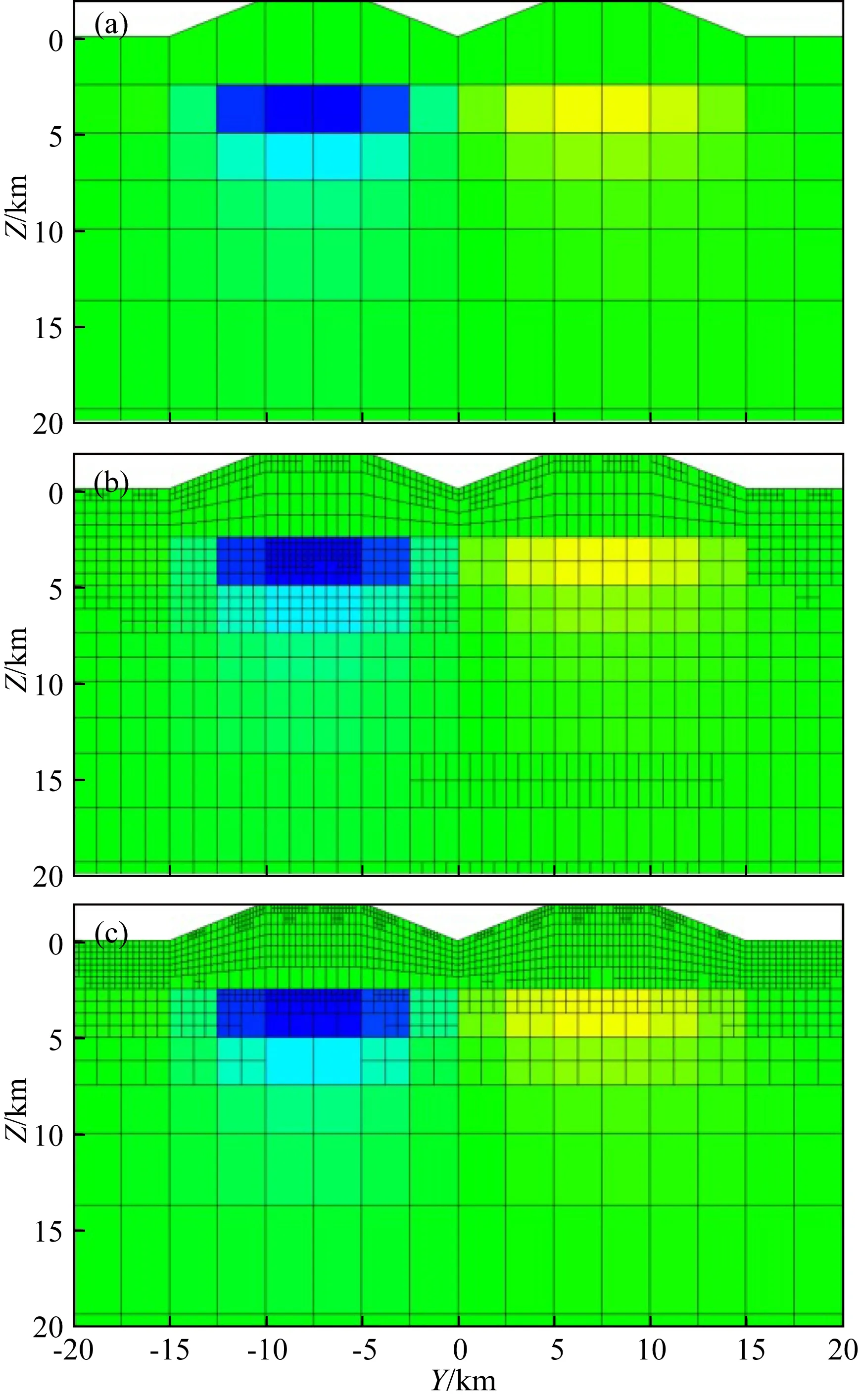
4 结论