热辐射成像法测量大型炉膛内三维温度场的算法新进展

闫慧博，唐广通，李路江，汪潮洋，李 欣，闫晓沛，李智聪，娄 春

(1.国网河北能源技术服务有限公司，河北 石家庄 050021；2.华中科技大学 能源与动力工程学院 煤燃烧国家重点实验室，湖北 武汉 430074)

0 引 言

在碳达峰和碳中和愿景下，一方面，火电企业的发电小时数将被进一步压缩，承担更多的调峰任务，火电机组会更多地在50%以下的低负荷运行；另一方面，火电机组将高比例掺烧高水分、高灰分经济煤种甚至污泥、生物质等燃料，锅炉的运行条件会严重偏离设计工况。在这些现实情况下，火电机组锅炉的清洁、经济、灵活运行，低负荷稳燃、水冷壁安全、主/再热汽温偏差等问题将更为突出，迫切需要对火电机组发电智能化实施技术升级，其中的关键技术之一是实现大型炉膛的三维、实时、数字化监测[1-3]。

大型炉膛内燃烧温度的三维空间分布正常与否，关系到炉内燃烧过程的安全性、经济性和污染物的排放水平。一方面，整体温度水平的高低与机组的负荷控制密切相关，一定的负荷输出对应着一定的炉内温度水平；另一方面，火焰中心高度偏离设计条件，将影响锅炉热经济性和出力，火焰中心在水平面上的偏斜，会引起火焰刷墙、水冷壁结焦甚至水冷壁爆管事故[4]。文献[5]指出，非接触式测温方法是火电机组锅炉炉内火焰等特殊环境温度测量的主要发展方向。但常见的火焰发射光谱、火焰图像处理技术都是视线检测技术，传感器接收的信号都是视线上的辐射累积，该类方法得到的温度结果是沿视线的平均值。要实现燃烧场中三维温度分布测量，必须通过平面激光、层析成像或热辐射成像[6]。而迄今为止已实际用于大型炉膛内三维温度场可视化监测的技术仅有声学层析成像法、吸收光谱层析成像法以及热辐射成像法[3,7]。

其中，声波在不同温度的介质中传播速度不同，是声学测温方法的原理。而声学层析成像法则是利用声源、声波导管和声波接收器等设备，根据多条路径上的声波飞渡时间来求解三维温度分布，即在得到每条路径上的声波飞渡时间数据后，建立温度场各离散网格温度值与声波飞渡时间值之间关系的代数方程组，将温度场的测量转化为求解方程组[8]。华北电力大学已将声学层析成像法用于国内200、600 MW等火电机组燃煤锅炉中三维温度场的在线监测[9]。

气体分子对于激光的吸收具有波长选择性，基于此原理，特定波长的激光穿过一定浓度的特征气体时会因吸收而减弱，并且衰减程度与气体的温度、压力、浓度以及激光路径均有关系。因此可以通过测量吸收前后的光强确定衰减程度，计算气体的浓度和温度等参数。基于可调谐二极管激光吸收光谱技术的发展，实际应用时将其与层析成像结合，用于测量燃烧火焰组分浓度和温度的二维分布[10]，国外已有部分火电厂利用可调二极管激光吸收光谱技术，安装激光发射及接收器等设备，测量锅炉炉内温度和气体浓度[5,11]。

国内著名燃烧测量专家周怀春教授在20世纪90年代首次提出了测量炉内三维温度场的热辐射成像法[12]，该方法基于燃烧自发辐射信息，由辐射传递方程建立热辐射成像模型，并考虑炉内燃烧介质和壁面的发射、吸收、散射(反射)作用。该模型将炉内燃烧温度、辐射特性(组分浓度)与炉膛边界上电荷耦合器件(Charge Coupled Device,CCD)摄像机检测到的热辐射图像联系起来，建立定量关系，炉内三维温度分布利用辐射传递反问题结合成像模型求解获得[4,6-7]。在实际应用中，热辐射成像法使用的设备通常是CCD摄像机，具有系统紧凑、易于实施等特点。相对于声学层析成像法和吸收光谱层析成像法的空间分辨率受路径限制、时间分辨率较大的缺点，热辐射成像法的空间分辨率与图像像素有关，且响应较快，因此时空分辨率较高，具有较大的应用潜力，目前已用于国内200、300、660 MW等十多台火电机组锅炉内三维温度场的在线监测中[13-16]。

结合大型炉膛内三维温度场可视化监测技术的实际应用情况，笔者将从热辐射成像模型及辐射传递反问题求解方法2个方面阐述相关的研究现状，对热辐射成像法测量大型炉膛内三维温度场的发展趋势和动态进行探讨。

1 大型炉膛内热辐射成像原理

1.1 热辐射成像模型

炉膛内燃烧介质和壁面发出的热辐射信号是一种光信号，其表征具有多种维度，如图1所示，在某一时刻t，位于炉膛边界上O(x,y,z)处的CCD摄像机接收到来自s(φ,θ)方向上的热辐射光束，其中x，y，z为三维空间的任意位置；φ、θ为热辐射光束的传播方向；λ为所采集热辐射信号的光谱信息；t为热辐射信号捕获的时刻。

炉膛系统是具有发射、吸收、散射特性的燃烧介质被具有发射、吸收、反射特性的壁面包围形成，固体壁面的发射、吸收和反射都在表面进行，而燃烧介质的发射、吸收和散射则在整个炉膛容积中进行，这使得热辐射成像不同于一般的光学成像。在热辐射成像过程中，位于炉膛边界上的CCD摄像机被视为一个接受燃烧空间辐射能量分布的二维传感器，就辐射而言，其接受到的能量包括壁面辐射和到达CCD的整个容积的辐射；就吸收和散射而言，投射到CCD上的能量在辐射行程中被沿程的介质吸收和散射而逐渐降低。因此，CCD摄像机接受的能量可分为4部分：壁面发射能量经介质吸收后的壁面直接辐射，介质发射能量经介质吸收后的介质直接辐射，壁面和介质发射能量经壁面反射后的壁面间接辐射，壁面和介质发射能量经介质散射后的介质间接辐射[17]。

图1中，位于炉膛边界O点处的CCD摄像机在s方向接受的能量信息被除以每个像素的成像面积和立体角后，可转化为辐射强度I(O,s)，结合辐射传递方程，包含了壁面直接辐射、壁面间接辐射、介质间接辐射、介质直接辐射的辐射强度I(O,s)可写为

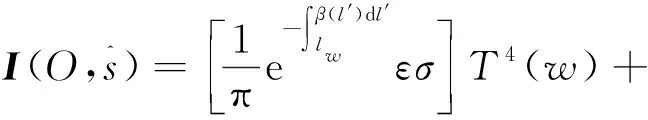
(1)

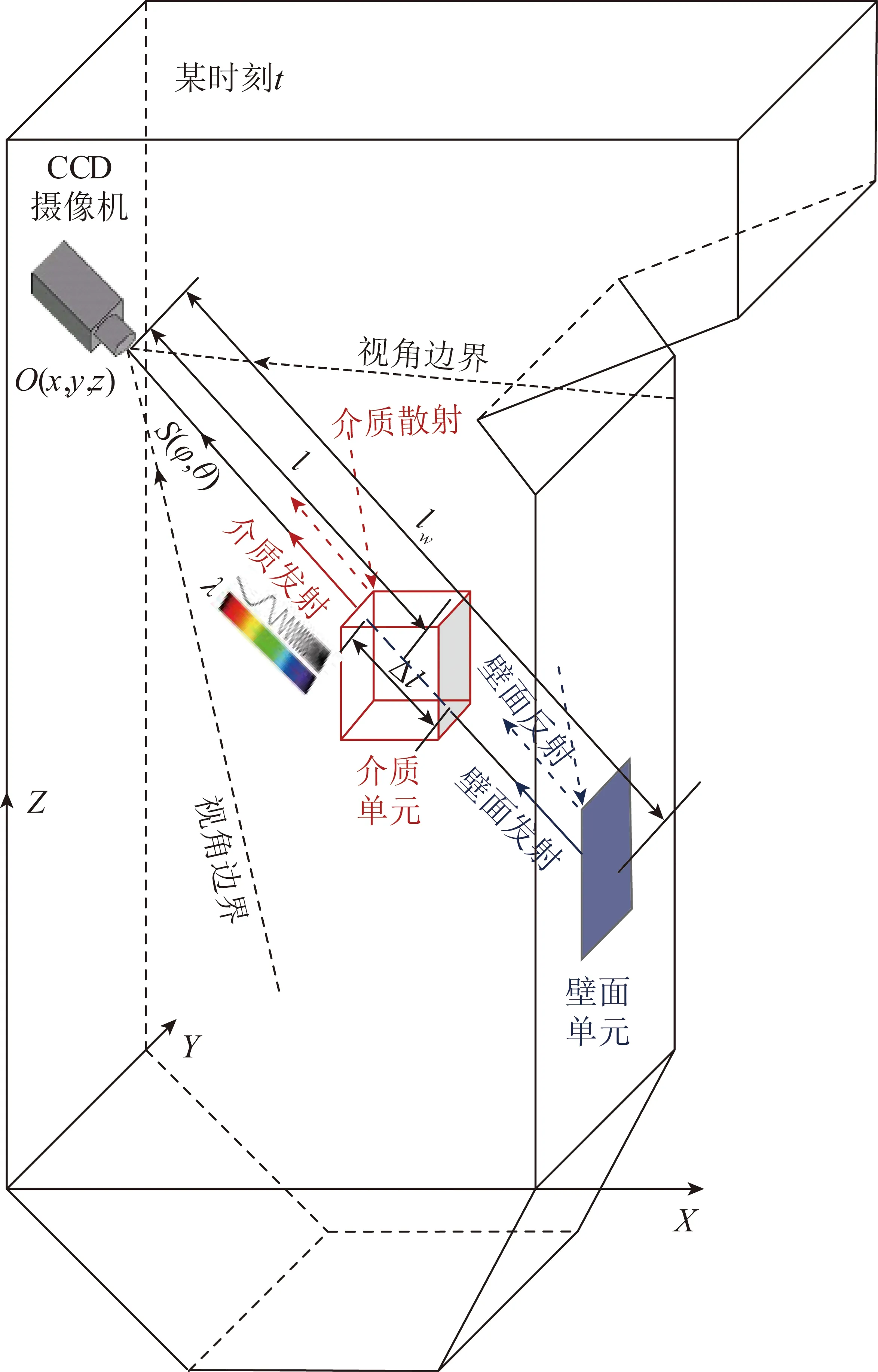
图1 一条视线方向辐射强度Fig.1 Radiative intensity in a line-of-sight direction

(2)

即：

I=A1Tg+A2Tw=AT，

(3)

1.2 热辐射成像矩阵的计算方法

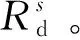
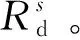
(4)

式中，i0、j0、k0为能量追踪起始点的坐标；il、jm、kn为能量追踪终点坐标。

具体步骤包括：① 介质或壁面单元中能束的发射位置和方向由随机选取的随机数确定；② 采用路径长度法确定能束传递路径及其能量衰减的处理，单元吸收导致能束能量的衰减，单元散射或反射则改变能束的传递方向；③ 能束跟踪过程一直重复，直到能束携带的能量被减少到某一极限小值。从一个单元发射的所有能束的跟踪计算结束后，得到这个单元对所有单元的DRESOR数。随后依次将每个考虑的单元作为发射单元进行计算，得到所有的DRESOR数。图2给出了一维轴对称系统中介质单元DRESOR数的分布，即每个介质单元发射的能量被所有介质单元散射的份额分布，由图2可知，介质单元对自身的散射影响最大，而且远离轴心的介质单元(第50个网格单元)，自身对自身的散射贡献更大。

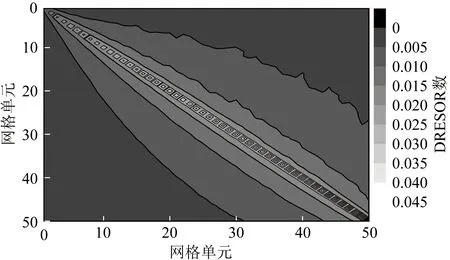
图2 DRESOR数分布Fig.2 Distribution of DRESOR values

如前所述，基于蒙特卡洛法的路径长度法、计算热辐射成像矩阵的DRESOR法是以各网格之间的DRESOR数的计算为核心，通过大量的能束跟踪进行求解(能束数的选择一般在10 000条以上，以确保计算的准确性)。为避免蒙特卡洛法产生的统计误差，以及多条能束追踪耗时较长的缺点，王贵华[19]提出了解方程DRESOR法，假设系统发射单元为黑体，而其他单元均不发射。系统内的辐射强度简化为仅由具有发射能力的微元体引起，其表达式仅为DRESOR数的函数，建立一系列方程组，通过方程组求解直接得到DRESOR数。具体步骤为：① 对辐射强度公式进行离散并划分系统网格，选定初始发射单元，设定其为黑体发射并且相对能量为1.0，其余网格均不发射；② 针对第i个网格，给出其中心点辐射强度的简化表达式，并根据入射辐射相等建立DRESOR数的方程；③ 改写方程为矩阵方程形式，并引入2或3阶指数积分函数进行求解。HUANG等[20]将该方法应用于三维发射、吸收、散射介质系统的辐射强度计算中，结果表明：在能束数为10 000条时，解方程DRESOR法的精度要高于DRESOR法，且计算效率提高3个数量级。

此外，刘冬[21]提出采用逆向蒙特卡洛法求解热辐射成像矩阵。正向蒙特卡洛方法需要追踪大量无法达到CCD摄像机的能束，这些无法到达接收区域的能束对结果没有贡献，从而导致计算效率低。而逆向蒙特卡洛法则是利用正向法的基本思想，反向跟踪统计结果，所追踪的每条能束都对摄像机成像有贡献，在不需要大量计算的前提下能较好地解决问题。牛春洋[22]提出吸收、发射、散射性介质任意方向辐射强度计算的广义源项多流法，这是一种在有限体积法基础上发展的热辐射成像矩阵的计算方法。该方法的思路是：利用有限体积法计算出系统中所有网格对应的源项，即广义源项；在源项已知的条件下，辐射传递方程转化为纯吸收介质中的纯微分方程，根据沿探测方向分段积分的方法从入射边界逐单元计算到介质的出射边界，从而得到介质任意方向上的辐射强度分布。该方法兼顾了计算效率和计算精度，既具有有限体积法的高效率和广泛适用性，又具有接近于蒙特卡罗法的计算精度。

2 辐射传递反问题求解方法

2.1 辐射传递反问题的不适定性分析

在热辐射系统中，由系统向外界射出的辐射信号反演重建系统内部参数或边界条件，这类问题称为辐射传递反问题。按应用目的又可以分为测量问题和反设计问题，从CCD摄像机所接受的炉内出射辐射信号重建炉内三维温度场属于前者。在数学特征上，这类辐射传递反问题具有严重的不适定性[23]，主要体现在2方面：一方面，反问题中的输入数据为欠定或过定，即测量的辐射强度数据远多于待求的温度数据，从而导致解的不唯一性甚至解的不存在性；另一方面，反问题的解对于输入数据往往不具有连续依赖性，即辐射强度数据的微小测量误差会引起温度场重建的不稳定。

首先是辐射成像过程对方向的选择性。CCD摄像机每个像素只对空间很小立体角内投射而来的辐射敏感，即位于很小立体角范围的空间点的温度对该像素接受的辐射信号具有明显贡献，表现为成像矩阵中对应元素的数值非0，且取值较大；相反，位于很小立体角范围之外的空间点的温度对该像素接受辐射能的贡献很小(当介质具有散射特性或壁面具有反射特性时)，甚至为0(介质无散射且壁面无反射)，表现为成像矩阵中对应元素的数值很小，或为0。这是造成成像矩阵在形式上表现为稀疏矩阵的第1个原因。

第2个原因是燃烧介质对辐射信号的衰减作用。对位于成像像素立体角范围之内的空间点，当这些点距CCD摄像机很远时，其辐射在空间传递过程中的衰减随距离的增大而显著增大，导致实际达到CCD摄像机的有效能量越来越小。这样会使成像矩阵中对应元素的数值越来越小，增加该矩阵的奇异性。

对于成像矩阵条件数很大的不适定问题，其求解方法主要有优化方法和正则化方法2类[24-25]，而优化方法又可分为基于梯度计算的传统优化方法和基于概率搜索的智能优化算法。

2.2 炉内温度场重建的传统优化方法

传统优化方法属于确定式算法(Deterministic Algorithm)，其求解过程如下：首先假定待重建参数的分布，然后通过控制方程的正问题求解得到测量参数的计算值，这个计算值与实际测量的结果存在差异，通过修正重建参数，反复迭代运算，当表征吻合良好性的目标函数减小到一个可以接受的数值时，迭代结束。当未知量的估计值沿着最大速度逼近目标函数最小值方向变化，该迭代逼近效果最佳。

以式(3)中重建炉内三维温度场为例，用Ical、Imeas分别表示辐射强度的正问题计算值和实际测量值，定义目标函数F(T)：

(5)

当Ical(T)最接近Imeas时，目标函数F(T)被最小化。而目标函数取决于一系列待求向量T，这将反问题的求解转换为一个最小化问题，目的是找到一系列T*满足F(T*)=min[F(T)]。如果F(T)光滑且连续可微分，则可基于梯度最小化从初值T0迭代得到T*。在第k次迭代中：① 检测Tk是否能让F(T)最小化，通常是看∇F(Tk)是否为0；② 如果Tk不等于T*，根据F(Tk)的局部曲率选择一个新的搜索方向pk；③ 最小化f(Tk)=F(Tk+αkpk)，得到步长αk；④ 如果有必要可以对αk或pk进行约束或修正，使得Tk+αkpk在一个合适的区域内；⑤ 得到重建参数的更新值，Tk+1=Tk+αkpk。

搜索方向根据目标函数的一阶灵敏性系数确定：

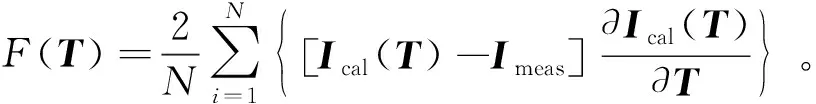
(6)

如果得到的所有测量值都在给定的相对误差范围内，就可以认为迭代可以收敛。

典型的传统优化方法有最小二乘法、共轭梯度法、最速下降法、牛顿法等[25]。LIU等[26]用共轭梯度法开展了三维炉膛系统中温度场反演的模拟研究，结果表明，即使介质辐射特性等参数存在随机测量误差，对温度场反演精度的影响也不大，相对误差始终小于15%；韩曙东[27]提出了加先验经验的最小二乘法，并用于300 MW机组锅炉的温度场重建试验，重建结果能较好地还原高低温区的位置及低温区的数值；王飞等[28]采用代数重建技术获得了300 MW机组燃煤锅炉的截面温度场，并对数值计算结果进行对比分析，温度相对误差小于50 ℃；黄群星等[29]提出了基于二元矩形插值公式的滤波反投影重建算法，快速重建出300 MW 电站锅炉内的准三维温度场。上述传统优化方法虽然能完成炉内温度场的重建，但也存在如下局限性：① 对初值依赖大，如果初值设置不合理，重建结果会很差，甚至找不到最优解；② 需要求目标函数的导数(梯度)，有的还要求目标函数一阶导数连续；③ 属于局部优化算法，无法获得全局最优解。

2.3 炉内温度场重建的智能优化方法

随着计算机技术的高速发展，具有仿生行为特征的智能优化算法受到广泛关注，也被大量用于辐射传递反问题的求解中[30]。作为一种启发式算法(Heuristic Algorithm)，智能优化算法是从某一个随机解出发，按照相应的算法机制，以一定的概率在求解空间中寻找最优解。根据模拟对象的数量不同，智能优化算法又可分为基于生物群体模拟的智能优化算法和基于生物个体模拟的智能优化算法，前者包括微粒群算法(Particle Swarm Optimization,PSO)、蚁群算法(Ant Colony Optimization,ACO)、遗传算法(Genetic Algorithm,GA)等，后者包括人工神经网络(Artificial Neural Network,ANN)、支持向量机(Support Vector Machine,SVM)等。这类基于概率搜索的优化算法与传统优化算法相比，无须已知优化问题的精确数学模型，也无需求解目标函数的梯度，采用启发式的概率搜索，能够得到全局最优解，且不依赖于初始条件。

群体智能优化算法的结构形式相似，如图3所示。先通过初始化给出反问题可能解的一个子集，然后在该反问题的解空间内，对这个子集施加某种算子操作，得到一个新的子集，重复对新子集进行某种算子操作，直到该子集包含最优解。不同的群体智能优化算法所采用的算子操作不同，更新规则不同。当前发展较成熟且已在测量相关辐射传递反问题中得到广泛应用的主要是微粒群算法和蚁群算法。

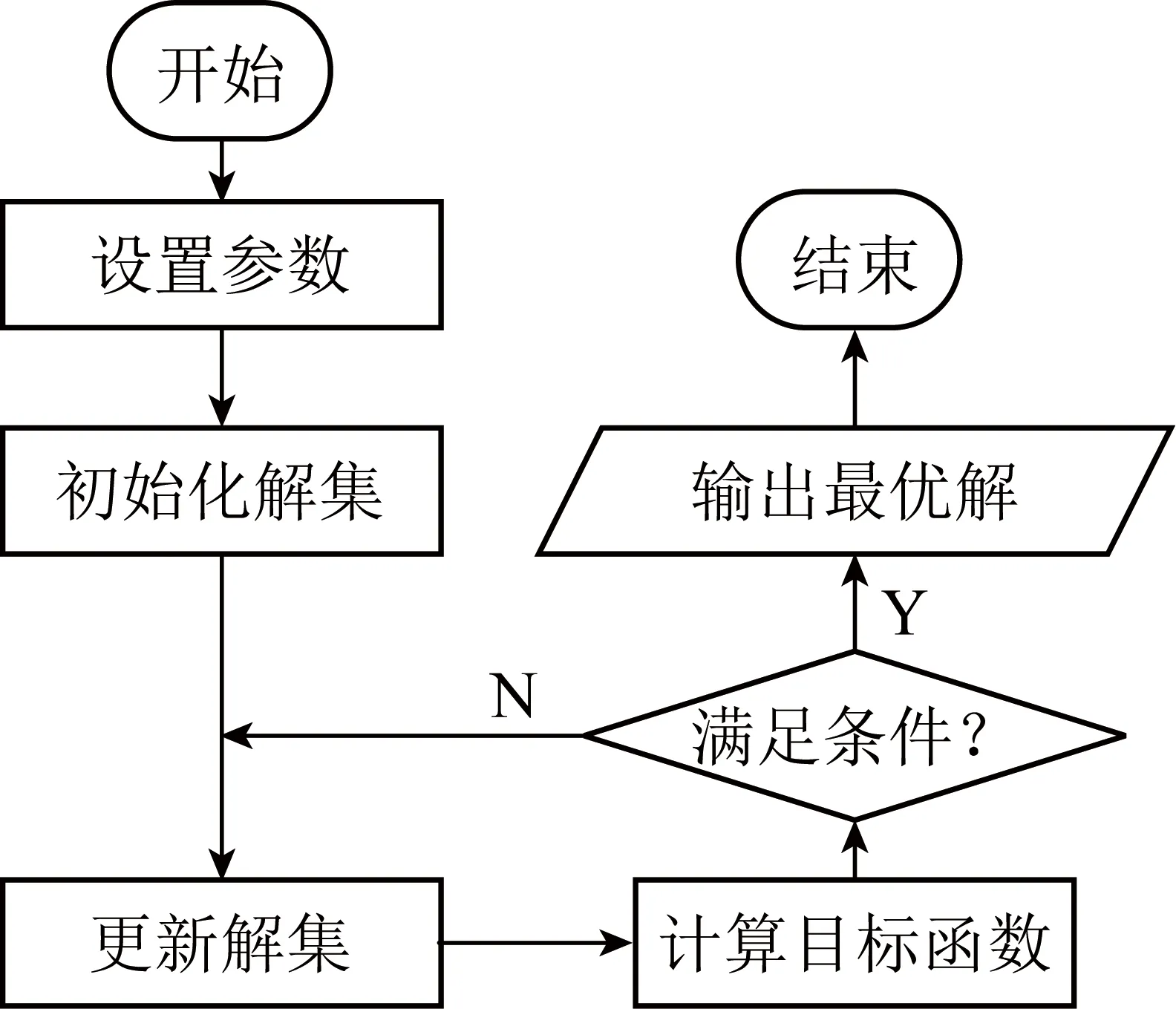
图3 群体智能优化算法基本框架Fig.3 Frame of swarm intelligent optimization algorithm

微粒群算法的思想源于鸟类群体觅食行为[31]鸟群在寻找食物过程中，开始比较分散，逐渐聚成一群，最后找到食物。将觅食区间中的每只鸟看作一个粒子，鸟的飞行速度表示粒子的速度，每只鸟的位置是粒子的位置，同时也代表优化问题的一组解，而食物的位置则表示优化问题的最优解，并通过迭代搜索得到区域内粒子的最优位置。迭代过程中，粒子自身位置的更新是通过将当前位置向量与更新速度后速度向量进行叠加实现，而速度向量的改变则与其自身速度及其历史飞行经验和群体飞行经验相关，并受最大和最小飞行速度的限制。QI等[32]首次利用微粒群算法反演了吸收、发射、散射介质中的辐射源项；孙亦鹏等[33]采用随机微粒群算法从乙烯扩散火焰出射辐射强度分布中同时重建了火焰中温度和碳黑浓度分布，2种特性的重建结果相对误差均小于2%；LIU[34]也用随机微粒群算法开展了温度场与介质辐射特性同时重建的模拟研究。

蚁群算法是通过模拟自然界蚂蚁群体寻优行为提出[35]，蚂蚁在觅食时总能绕过障碍物找到从蚁巢到食物源的最短路径，原因是蚂蚁在发现食物后返回蚁巢搬救兵的路上会留下一种信息素，其他蚂蚁发现信息素后，在选择路径时会选择信息素大的路径。随着时间推进，较短的路径上累积的信息素浓度逐渐升高，选择该路径的蚂蚁个数也越来越多，最后整个蚁群都会集中到最佳的路径上。如果用蚂蚁的行走路径表示待优化问题的可行解，整个蚁群的所有路径构成待优化问题的解空间，蚁群最终找到的最佳路径对应的便是待优化问题的最优解。齐宏等[30]已将蚁群算法用于稳态辐射-导热耦合反问题、瞬态辐射传递反问题的求解中。

此外，在基于生物个体模拟的智能优化算法中，人工神经网络通过模拟人脑神经元的结构，按不同的连接方式组成不同的网络，实现深度学习求解各种优化问题[36]。该算法能够无需事先确定输入输出之间映射关系的数学方程，仅通过自身的训练学习规则，在给定输入值时得到最接近期望输出值的结果。常用于辐射反问题求解的是前馈神经网络(Feedforward Neural Network,FNN)。图4给出了其基本构架，各神经元分层排列，每个神经元只与前1层的神经元相连，接收前1层的输出，并输出给下1层，各层间没有反馈。根据网络结构的不同又包括：多层感知器神经网络(Multi-Layer Perceptron Neural Network,MLP)，卷积神经网络(Convolutional Neural Network,CNN)，极限学习机(Extreme Learning Machine,ELM)等。

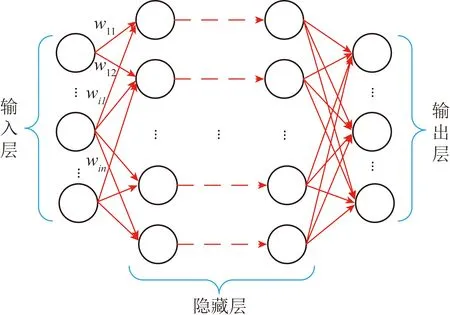
图4 前馈神经网络的基本构架Fig.4 Basic architecture of feedforward neural network

现有研究中，MLP、CNN、ELM已被用于从边界出射辐射强度中重建燃烧火焰的辐射源项、温度及组分浓度分布，且具有较高的重建精度(小于3%)。YU等[37]将虚拟火焰样本的边界辐射强度作为输入数据，利用极限学习机重建火焰的辐射源项。JIN等[38]提出了一种基于卷积神经网络的三维快速火焰化学发光层析成像重建系统，测量结果证明，CNN模型能够以可靠的精度和结构相似性从实时捕获的投影中重建火焰三维结构。REN等[39]利用多层感知器神经网络，将平面燃烧器的红外光谱辐射作为测量数据，反演温度分布和气体组分浓度。WANG等[40]开发了一种两步多层感知器神经网络，以协助基于碳烟辐射的温度测量方法来反演层流扩散火焰温度场，结果证明该方法表现出较强的预测稳定性。李智聪等[41]选用多层感知器神经网络，从乙烯层流扩散火焰的高光谱辐射强度中预测了火焰温度和碳烟浓度分布，并评估了MLP模型的预测和抗噪能力。

上述智能优化算法的发展为大型炉膛内三维温度场重建提供了新的手段和思路，WEI等[42]采用遗传算法重建了一台四角切圆燃烧炉内的三维温度场，相对误差约为1%；许烨烽等[43]采用多层感知器神经网络建立了深度学习模型，开展了大型炉膛内横截面温度场重建的模拟及试验研究，初步检验了人工神经网络算法在重建大型炉膛内三维温度场的可靠性。

需要注意的是，经过训练后的人工神经网络模型能够快速完成温度、辐射特性的重建，但网络训练还需要大量数据集，这是影响重建精度的关键因素之一；群体智能优化算法虽然不需要大量训练数据，但需要构建目标函数搜寻全局最优值，重建温度场所需时间也相对较长，有待进一步提高效率，以实现炉内温度场的在线测量。

2.4 炉内温度场重建的正则化方法

20世纪60年代，前苏联学者吉洪诺夫提出了处理不适定问题的正则化方法(Regularization Method)，这使得反问题的研究进入了一个新的阶段，其基本思想是：用一族与原不适定问题相邻近的适定问题的解去逼近原问题的解[44]。典型的正则化方法有吉洪诺夫正则化(Tikhonov Regularization,TR)、截断奇异值分解(Truncated Singular Value Decomposition,TSVD)、最小二乘QR分解(Least Square QR decomposition,LSQR)等。下面以式(3)建立的热辐射成像模型为例，分别介绍这3种正则化方法重建温度场的原理及应用。

ZHOU等[45]提出了修正的吉洪诺夫正则化方法，其基本原理是寻求T使得式(7)极小化：

(7)

其中，D为正则化矩阵，用于建立相邻单元之间的温度分布连续约束关系；α为正则化参数，用于控制连续约束关系的强弱。在极小式(7)的情况下式(3)的正则化解为

T=(ATA+αDTD)-1ATI。

(8)

目前，该方法在实际炉膛内三维温度场重建中得到了较广泛应用。文献[13-16]给出的200、300、660 MW燃煤机组锅炉内三维温度场结果，都采用修正的吉洪诺夫正则化方法重建，并与抽气热电偶、高温计等测温方法进行对比，偏差在5%内，重建的结果能给出炉膛三维空间内全场温度分布，并反映炉内燃烧工况的变化，对于预防炉膛熄火、提高燃烧稳定性、分析炉膛辐射换热具有重要作用[46]。此外，修正的吉洪诺夫正则化方法还被用于轧钢厂步进式加热炉[47]、石油化工厂管式加热炉[48]、化工厂裂解炉[49]、单火嘴燃烧炉[50-51]等燃油或燃气工业窑炉内三维温度场的可视化重建中，为改进生产工艺、提高产品质量提供指导。需要注意的是，式(7)中若α=0，反问题的解为最小二乘解；若α趋近于∞，则得到均匀的温度分布。这表明正则化参数的取值对温度场重建结果有较大影响，通常可采用L曲线准则法选取正则化参数[52]，但需大量计算时间。为解决这个问题，QIU等[53]提出了一种基于三次样条插值的正则化重建和广义奇异值分解的混合方法，用以提高正则化参数的选取精确和效率，结果表明，此方法能得到理想的正则化参数，进一步提高三维温度重建精度及效率。

截断奇异值分解是一种矩阵因式分解技术[54]，首先，把成像矩阵A的奇异值分解的表达式为

(9)

其中，左奇异值向量ui和右奇异值向量vi分别为矩阵U和V为正交列向量；S为元素是奇异值的对角矩阵，Si满足：S1>S2>…>SN≥0。将容易造成不稳定的较小的奇异值直接截去，使原来的不适定问题转化为一个适定问题求解，可得式(3)的正则化解为

(10)

其中，整数p为截断参数，且p≤N，也称为正则化参数，其选取也可以采用L曲线准则。黄群星等[55]应用截断奇异值分解开展了三维温度场重建的模拟研究，通过分析不适定问题，发现在不同的模拟测量误差下，TSVD能成功得到合理的解，重建温度场的误差小于1%，能较好地再现原始假设温度场的特征。谢正超等[56]以10 m×10 m×10 m的三维炉膛为对象，对比分析了吉洪诺夫正则化和截断奇异值分解在炉内三维温度场重建中的效果优劣，结果表明：一般情况下吉洪诺夫正则化算法重建的温度场比TSVD算法重建的温度场误差要小，计算所需时间短，最高温度重建更准确。

LSQR算法是一种基于迭代的求解包含大型稀疏矩阵的最小二乘问题的算法，其基本思路是将复杂最小二乘问题转化为简单最小二乘问题，再采用基本的QR分解法求解[57]。刘冬等[58-59]采用 LSQR算法对三维温度场重建中的病态矩阵方程进行求解研究。结果表明，LSQR算法具有较好的数值稳定性和较强的抗测量误差能力，适于大型电站锅炉燃烧温度场特别是高温区的重建，误差小于1%，显示了其在温度场在线重建方面的潜力。

此外，考虑大型炉膛的尺寸及炉内颗粒浓度引起的消光效应，用热辐射法重建炉内三维温度场时，炉膛的光学厚度(系统尺寸与介质消光系数的乘积)是一个重要的影响因素。尤其是燃用煤粉、天然气、油、生物质、垃圾等不同类型的燃料时，炉膛的光学厚度也明显不同。并且，对于实际炉膛，除了光学厚度对三维温度场的影响之外，炉膛壁面有积灰、结渣等现象时，壁面发射率也会发生变化，同时也会影响温度场的重建。文献[60-62]分别采用上述正则化重建方法开展了炉内三维温度场重建的模拟研究，给出了不同的光学厚度、颗粒浓度、壁面条件下三维温度场的重建误差，结果表明：当光学厚度、颗粒浓度在一定范围内时，炉内三维温度场的重建能够较好再现真实温度场的分布特征。

3 结语与展望

热辐射成像技术与声学或吸收光谱层析成像均将温度场的测量转化为求解方程组，但2类方法截然不同。首先，声学层析成像和吸收光谱层析成像分别会引入声波、激光作为信号源，同时需要信号发射和接收装置，而热辐射成像则是利用炉内自发射热辐射信号，只需接收来自炉内的信号。其次，声学层析成像法和吸收光谱层析成像法的空间分辨率受路径限制且时间分辨率较大，而热辐射成像法的空间分辨率与图像像素有关，响应较快，具有较高的时空分辨率。并且层析成像是一种数学技术，是由低维投影数据反演高维目标的技术，基于投影，仅考虑了由于介质吸收引起的信号沿视线方向的衰减；而热辐射成像技术本质上是一种物理概念，基于辐射传递方程，除考虑介质和壁面的吸收外，还考虑由于介质在4π空间中散射及边界(壁面)在2π空间中反射引起的信号衰减。此外，现有的层析成像技术获得的是二维空间的数据，再通过逐层扫描获得三维空间的数据；而热辐射成像所考虑的介质发射、吸收、散射及壁面发射、吸收、反射过程是在三维空间进行，从根本上就是一种三维检测技术。

随着成像技术的发展，获取炉内热辐射信号的途径除了用CCD摄像机相机外，还能用光场相机、多光谱或高光谱相机等新型设备。相比于传统相机，光场相机不仅可记录投射到相机探测器上光线的强度，而且能分辨光线的方向；而多/高光谱成像仪则在每个成像单元测量大量连续波段辐射强度，能够提供包含空间和光谱信息的火焰辐射分布信息，为热辐射成像法用于大型炉膛内三维温度场重建指明了新的发展方向。