基于迭代的旋转视觉元件针脚位姿估计精度优化

邝泳聪，陈泽田

(华南理工大学 机械与汽车工程学院，广州 510640)

0 引言

插件机是将针脚电子元件插装到印刷电路板的精密组装设备，当前异形插件机采用的底部视觉算法简单直观，但由于部分元件底部反光较强，导致针脚图像提取困难，这影响了插件良率。插件机旋转视觉通过转动元件，从不同角度位置获取针脚的背光图像，有助于解决反光影响针脚识别精度的问题。

随着插件机的推广应用，除了保证精度外，插件效率上也提出更高的要求，当前高精度机型的插件模块，采用伺服电机一对一直接驱动，保证了定位精度，但其插件模块较重体积也难以缩小，因此高效率机型的插件模块设计，改由一个电机通过同步带拖动多个旋转轴，好处是减轻插件模块重量也便于缩小体积，不利因素是同步带存在弹性变形和齿隙，只做微小角度转动时，同步带传动的旋转轴可以满足插件精度要求，但做大角度转动时，角度旋转误差较大。前期旋转视觉研究主要针对高精度机型，该机型旋转轴的实际旋转角度与理论值非常接近(误差小于0.03°)，因此用旋转角的理论值计算针脚姿态，精度能满足要求。将旋转视觉应用到高效率机型时，由于实际旋转角与理论值差异大，用旋转角理论值估算针脚位姿，精度难以保证。常规的解决方案是每个旋转轴安装高精度旋转编码器，测量实际的转动角度，但这不但增加成本也不利于插件模块小型化，因此有必要从软件算法上寻找解决方法。

旋转测量时元件针脚之间相对位置固定，因此转动取像时所有针脚转过的角度相同。借鉴现有基于约束的优化方法，本文提出一种基于位置约束和迭代拟合的针脚位姿估计精度优化方法，通过上述针脚位置约束拟合出针脚的实际初始角和每次转过的角度。基于约束的优化是工程领域的一个重要课题，约束条件的存在限定了决策变量的可行范围，使解更具目的性。空间位置约束是一种常见的数学约束，通常表现为目标点相对参考系位置的几何关系。工程上已有诸多利用相对位置不变性进行后续处理的算法流程，多视图聚类根据多视角包含共同空间区域信息的一致性原则作为约束条件，从而对不同视角拍摄的对象进行聚类分析，ICP点云拼接则是根据刚性不变性估计变换矩阵并利用点云簇内部空间坐标相对不变的关系进行迭代的三维拼接。此外，在视觉标定中，Zhang式标定法利用了标定板角点相对位置不变约束完成空间点至相机坐标系的对应关系，根据目标结构特点，采用几何约束的方法是提升位姿估算精度的有效方法。文献[5]利用物体表面多种几何特征，如点与点、线与线的位置约束构造超定方程进而获得高精度的位姿估计。文献[6]根据物体几何不变性计算协方差从而提高深度相机的位姿估计精度；苏杰等通过夹持器的形状约束来对目标进行位姿估计；Hou等利用单目相机拍摄物体旋转不同角度的图片，并利用几何约束进行三维重建以提高精度，文献[9-10]基于相机成像线性特征实现对位姿估计的优化及高精度的畸变校正。

本文所提出的针脚位姿估计优化方法，利用元件各针脚相对位置固定的约束关系，将圆轨迹拟合与旋转角迭代拟合相结合获取实际旋转角的最优估计，进而得到精密的针脚位姿估计值。论文先建立基于位置约束的旋转角拟合模型，并从理论上分析了该方法的可行性；进而通过仿真分析该方法的精度与图像噪声、像素分辨率、针脚数和旋转取像点数等主要因素的关系，并进行效率分析，从算法精度和效率上验证了该方法的可行性。

1 针脚图像坐标与旋转角的函数关系

1.1 旋转视觉针脚位姿重构模型

针脚测量时旋转轴带动元件旋转，在不同的角度位置获取针脚的侧面图像。如图1～2所示，针脚末端在图中用点表示，理想情况下，旋转轴坐标系与世界坐标系重合且在摄像机坐标系的轴上，但由于加工和装配都会存在误差，旋转轴与世界坐标轴之间有一定夹角。

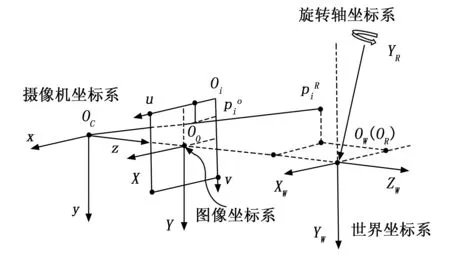
图1 旋转立体视觉成像模型

目标点

P

的旋转轴坐标系坐标与图像投影坐标间的转换关系为：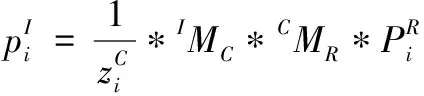

(1)

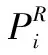
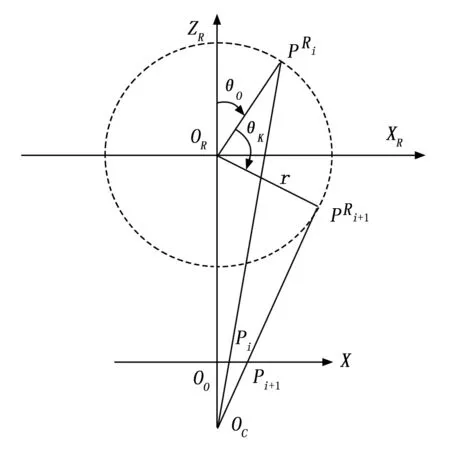
图2 旋转角与针脚图像投影的关系

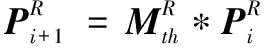
(2)

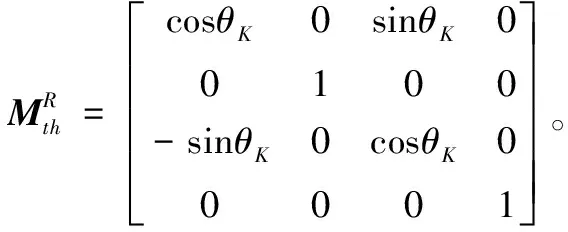
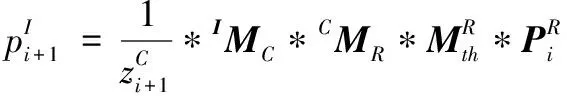
(3)

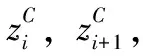
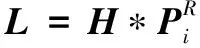
(4)

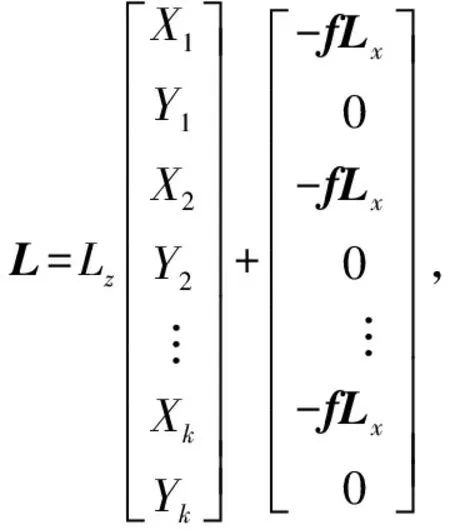
1.2 针脚图像坐标与旋转角的函数关系

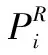
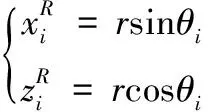
(5)

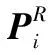
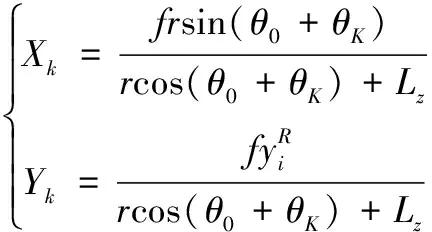
(6)

其中:

k

=1时

θ

=0。

2 针脚位姿估计的迭代拟合

2.1 基于位置约束的旋转角求解模型

1)针脚位置约束:

元件针脚旋转测量时，针脚间存在位置约束关系：元件多个针脚之间相对位置固定，因此每次转动取像时所有针脚转过的角度相同，从式(6)可知，在每个取像角度位置，每个针脚都会增加两个图像坐标方程，针脚越多增加的方程数越多，而待求变量只增加一个

θ

，本文所提出的旋转角拟合方法，就是通过上述的针脚位置关系拟合出各个针脚的实际初始角度位置

θ

和每次转过的

θ

。

2)旋转角求解模型 :

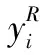
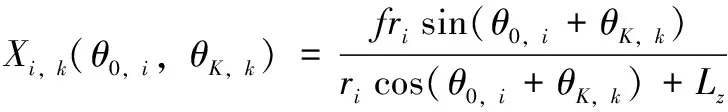
(7)

式中,

i

指元件第

i

个针脚，如

x

,指针脚

i

在第

k

个取像位置的

X

方向图像投影坐标，

r

是针脚

i

的旋转半径，

θ

0,指针脚

i

的初始取像角度，每个针脚位置不一样，因此每个针脚的初始角度不同；

θ

,(

k

=1,2…)指从初始取像位置转到第

k

个取像位置时转过的角度增量值，

k

=1时

θ

,=0。当

θ

0,和

θ

,已知时，根据式(7)可以得到针脚图像坐标的估计值。

3)旋转角拟合的可行性:

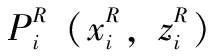
2.2 基于旋转角迭代拟合的针脚位姿估计

1)针脚位姿估计迭代拟合流程：

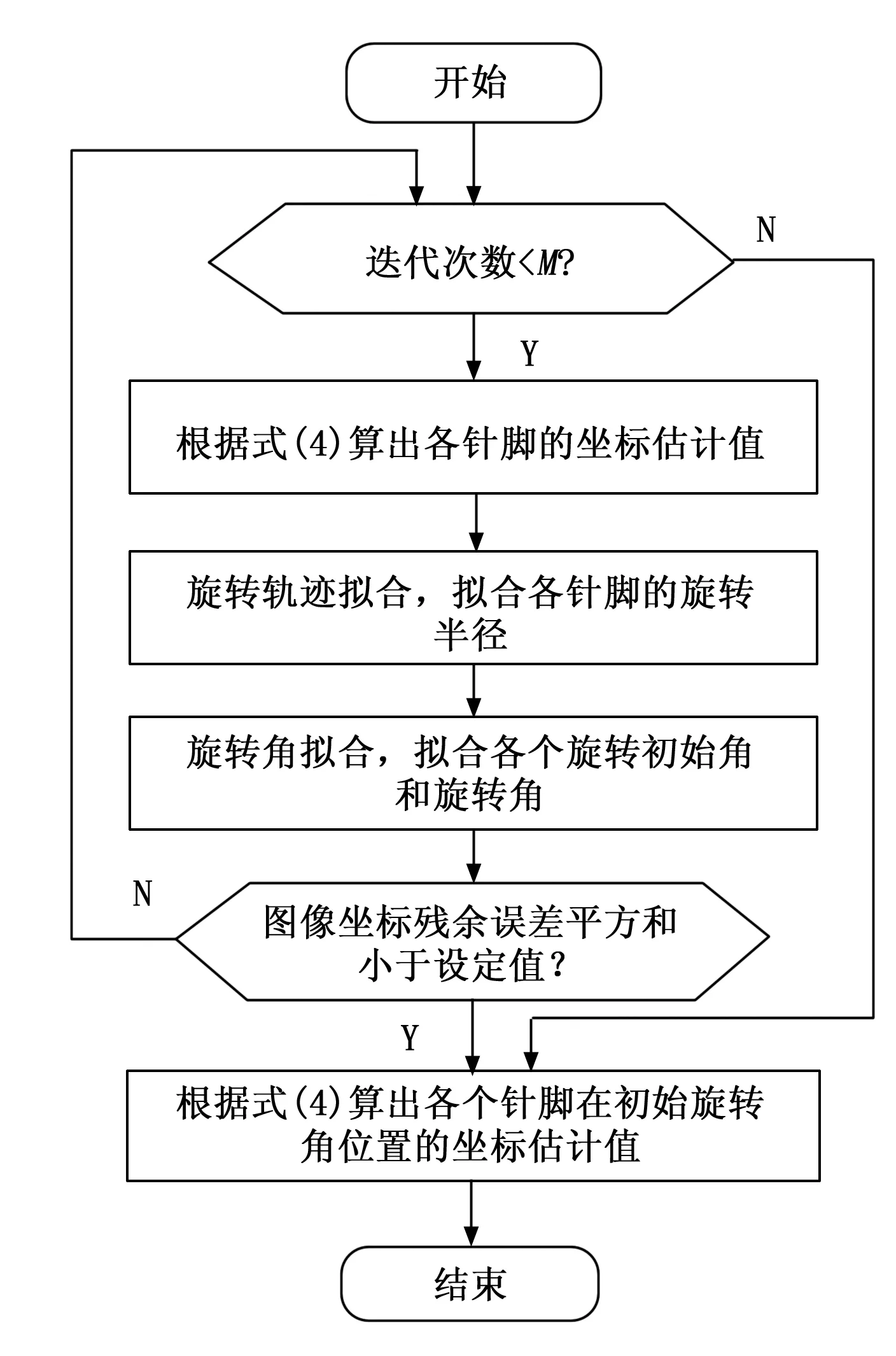
图3 针脚位姿估计的迭代拟合流程

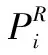
(2)旋转轨迹拟合:

除了因为定位偏差外，转动取像时针脚的轨迹都在圆周上。每个针脚与旋转中心距离不一样，因此各针脚的圆轨迹半径不同。针脚

i

的

k

个取像点所在的圆周轨迹方程为：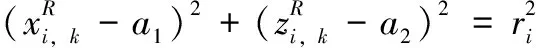

(8)

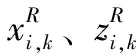
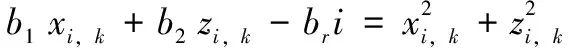
(9)

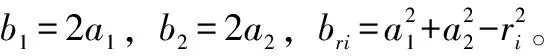
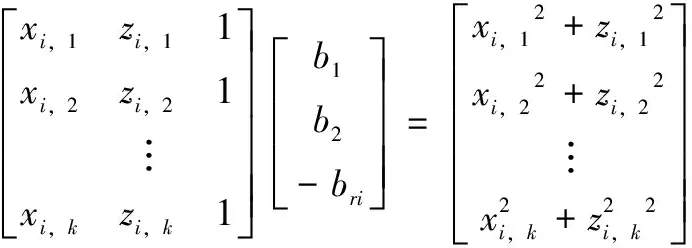
简记为：

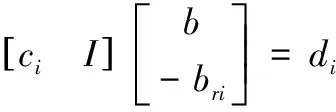
(10)

因为元件的所有针脚都同时绕旋转轴转动，因此所有针脚要对同一个旋转中心进行拟合，由式(10)得到

i

个针脚的圆轨迹拟合方程：

(11)

用奇异值分解等方法解式(11)，可得出各针脚旋转半径值及旋转中心。

3)旋转角迭代拟合：

根据式(7)构造的旋转角方程属于非线性方程，一般通过最小二乘法迭代拟合求解。基于迭代的最小二乘拟合是提升位姿估算精度的有效方法，文献[13]提出一种基于最小二乘的正交迭代算法，并通过实验证实该算法在提升相机位姿估计精度的有效性；文献[14]提出一种基于归一化图像平面中单应性误差的最小二乘解法以及一种迭代估计方法，实现了高精度的视觉测距；文献[15]运用随机霍夫变换与最小二乘结合，并根据聚类方法获得提取出PCB板真实的缺陷圆孔边缘；文献[16]根据最小二乘原理将工作台误差方程转化为正规方程，进行位姿的自校准；文献[17]基于自适应迭代加权最小二乘进行姿态追踪与几何重构等。

将式(7)通过泰勒级数展开为一阶导数形式，有：

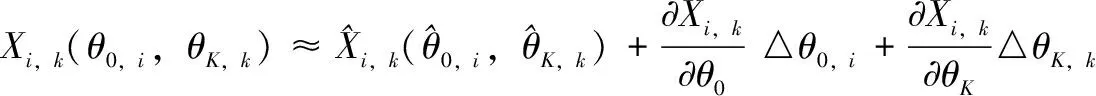
(12)

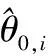
δX

(

θ

0,,

θ

,)=

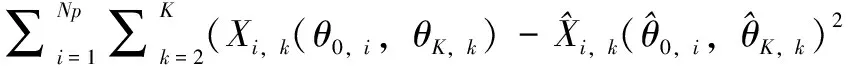
(13)

利用最小二乘方法迭代运算，令针脚图像的真实坐标和估算坐标的残余误差平方和

δX

(

θ

0,,

θ

,)逼近或达到全局最小，可得到

θ

0,和

θ

,的最优估计值。考虑到旋转角寻优范围比较小(初始值在±0.5°以内)和针脚测量的实时性要求，本文主要采用高斯-牛顿方法迭代求解式(13)。非线性方程的求解，主要是求解待求参数的调整量。对于针脚

i

，式(13)最小二乘解的雅可比矩阵、图像坐标残余误差

V

和旋转角参数调整向量△

θ

分别为：

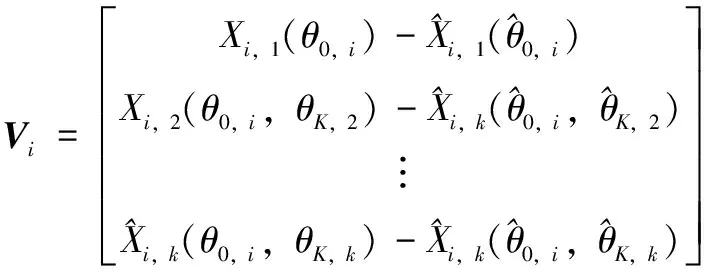
(14)

其中：0,对应矩阵的第一列，,对应矩阵的其余部分。元件所有针脚一起转动，因此在同一取像位置

k

各个针脚的旋转角偏差修正值赋予相同值△

θ

,；因为存在制造误差，相同型号的不同元件针脚间距也有微小差异，所以各针脚的初始角赋予独立的偏差修正值△

θ

0,。根据式(14)得到所有针脚联合求解的相应矩阵：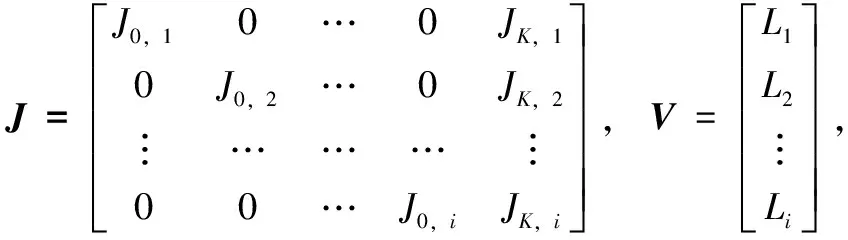

△=[△

θ

… △

θ

0,△

θ

,2△

θ

,3… △

θ

,[，=diag[

w

…

w

w

w

…

w

]是加权对角矩阵，针脚位姿估计主要根据

θ

的估计值，因此

θ

和

θ

赋予不同权值

w

和

w

。根据高斯-牛顿法可得到旋转角参数调整向量：△=(**)***)

(15)

第

j

次迭代后旋转角估计值修正为：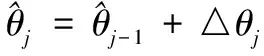

(16)

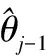
3 仿真实验与讨论

为验证本文所提出的针脚位姿估计优化算法的有效性，在Matlab2020a开发环境下对所提出方法进行仿真实验。除非特别说明，默认仿真参数如表1所示。其中图像噪声指图像离散误差之外的其它图像误差(包括图像畸变、热噪声等)；针脚真实坐标是在理论值基础上将元件整体在旋转轴坐标系

x

轴和

z

轴方向上做±1 mm以内的随机平移和±1°以内的随机旋转偏移得到；针脚的初始角

θ

0,根据各针脚的真实坐标与

z

轴的夹角，加上元件的初始测试角得到；根据各针脚的

θ

0,和

θ

,用式(7)算出无图像噪声的针脚图像坐标(计算时添加旋转轴径向跳动误差)；再添加图像离散随机误差和图像随机噪声则得到针脚真实图像坐标；图像离散误差、图像噪声和针脚真实坐标的随机偏移都是通过各自的幅值乘上表中的正态随机数得到；径向跳动误差按均匀分布产生。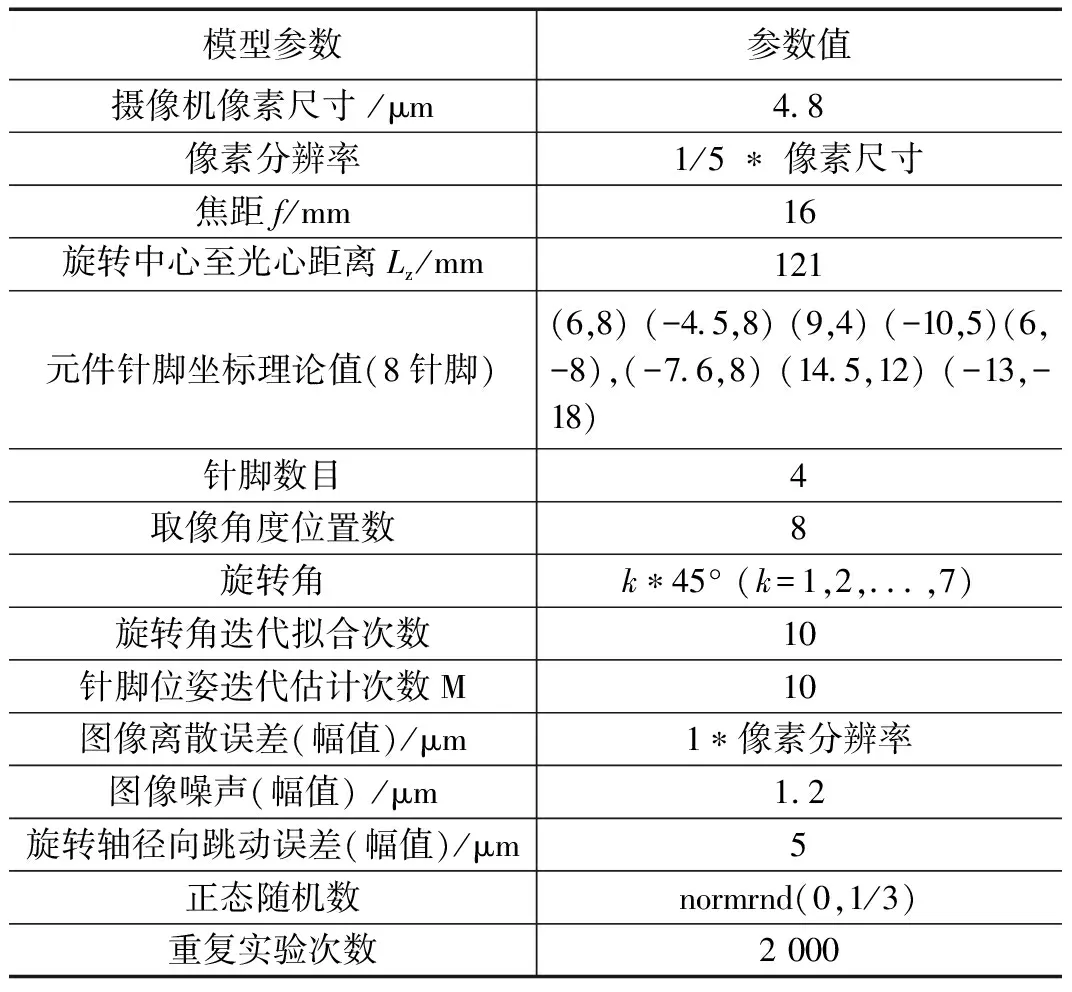

表1 仿真参数

重复实验为独立实验，每次实验的输入数据添加的相关误差或噪声都是重新产生。单次实验完成后，将针脚三维坐标的估算结果与针脚坐标的真实值比较，得到针脚位姿估算误差。重复实验完成后，对每次实验的数据统计，得到各个针脚位姿估计误差的均值

m

和方差

σ

。单次实验的结果有偶然性，为了保证仿真结果的可信度，用

m

±3

σ

作为针脚的位姿估计误差，将所有针脚位姿估计误差的最大值，作为重复实验的最终结果。

3.1 多针脚基于迭代法仿真

下文将分析本文所提出方法的针脚位姿估计精度与图像噪声、像素分辨率、针脚数和旋转取像点数等主要因素的关系。同步带传动的旋转轴大角度转动时，定位误差在±0.5°以内，因此设定旋转角误差的仿真取值范围为0.05°～0.50°。

1)迭代与非迭代：

按图3所示的流程，根据表1参数设置不同的迭代次数进行仿真，分析迭代次数对算法精度的影响。这里迭代次数指的是图3所示的

M

，

M

=1对应非迭代，即直接用旋转角理论值通过式(4)计算针脚位姿，不进行实际旋转角的迭代拟合；实验结果如图4所示。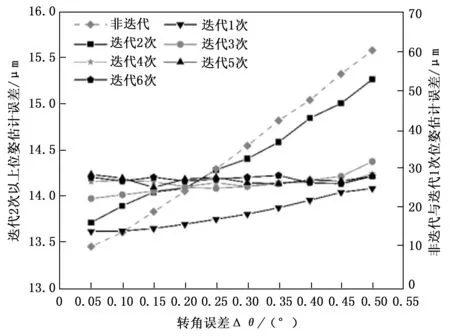

图4 迭代次数与位姿估算精度关系

由图4可见，非迭代算法的位姿估计误差与转角误差成正比；迭代算法明显提升了针脚估算精度，尤其是对于大的转角误差；增加迭代次数能进一步改善角度拟合精度，从而提升针脚位姿估计精度，迭代3次针脚估算精度已基本稳定；当旋转角误差较小(图中<0.1°)时，非迭代的针脚位姿估计精度比迭代略高，其原因是受图像随机噪声和像素分辨率的限制，下文将对该现象进一步说明。

2)图像噪声：

本小节分析针脚位姿估算精度与图像随机噪声的关系。图像随机噪声(幅值)分别取0.3 μm、0.6 μm、1.2 μm和2.4 μm，其它参数按照表1设置。

由图5(a)可见，图像噪声越大位姿估算误差越大；随机噪声最大幅值不变时，迭代拟合的针脚位姿估计精度几乎不受旋转角误差的影响；由图5(b)可见迭代估算误差与图像噪声成正比，图像噪声越小估算精度越高，0.5°以内的旋转角误差基本不影响位姿估计精度；

本文算法利用旋转测量时所有针脚具有相同旋转角

θ

,的特点，将所有针脚旋转方程构造成超定方程组解算

θ

0,和

θ

,，但每个针脚的图像坐标因噪声产生的误差都是独立且随机的，理论上本文算法对图像噪声引起的误差是无法抑制的。

3)像素分辨率:

一般情况下，摄像机的像素分辨率对图像测量的精度有直接影响，现有视觉检测技术都能达到亚像素分辨率，如MVTec 公司软件产品的边缘提取能力达到1/50像素，Keyence公司的IM-8000测量仪亚像素边缘提取能力达到1/100像素。本小节分析不同像素分辨率对针脚位姿估算精度的影响，像素分辨率分别取1/10、1/5、1/2和1倍摄像机像素尺寸，其它参数按照表1设置。

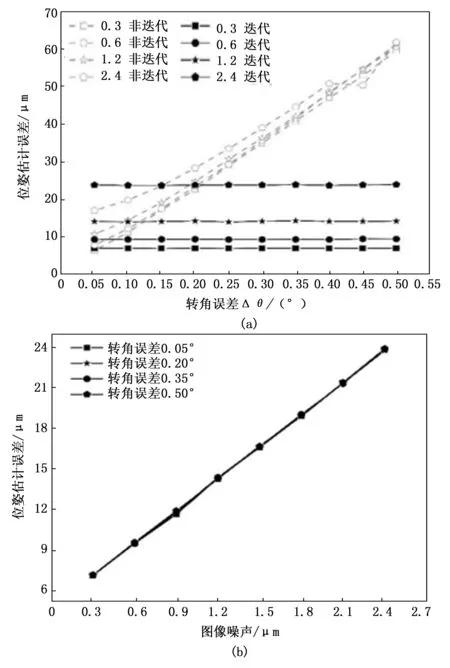
图5 位姿估计误差与图像噪声关系

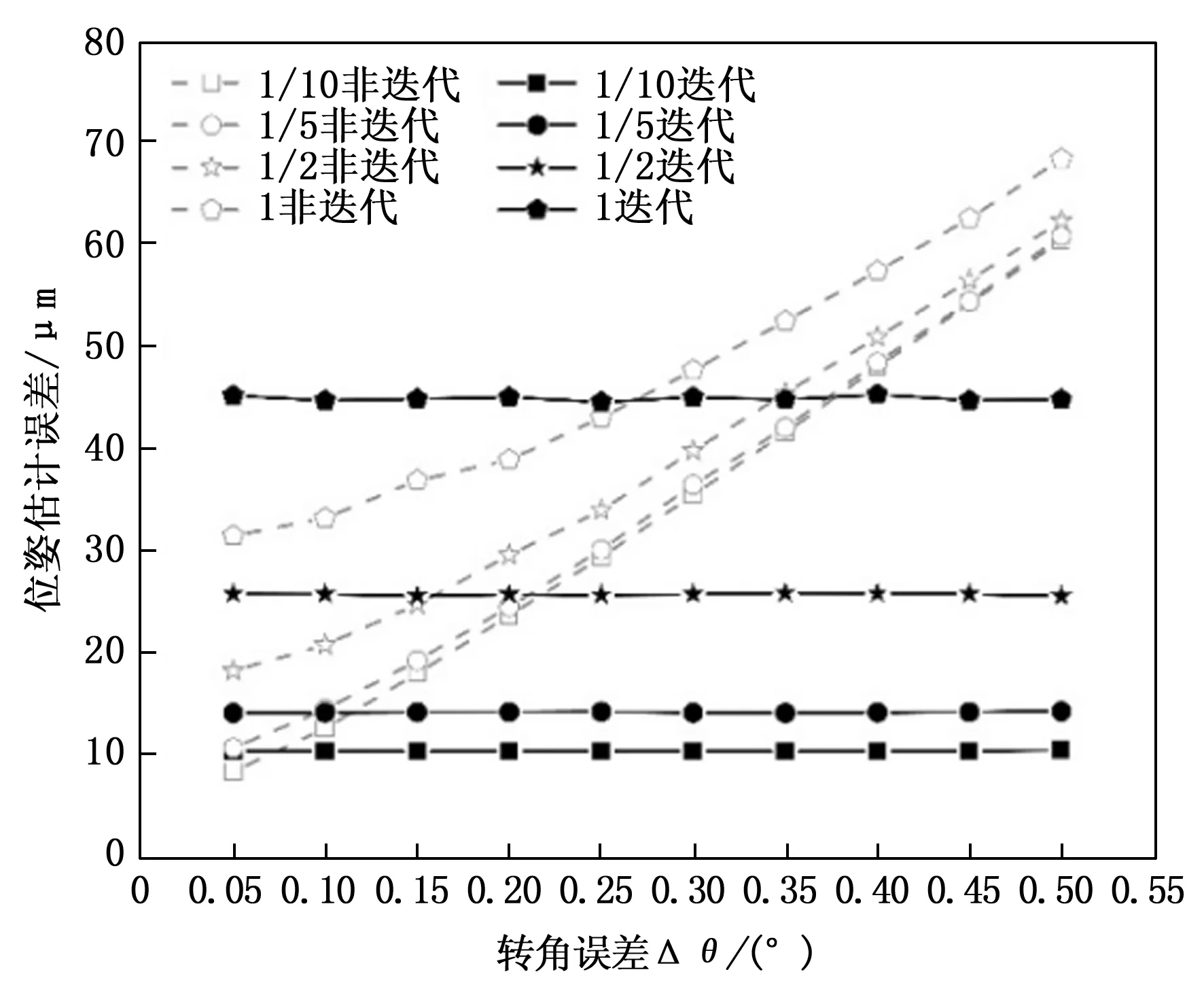
图6 像素分辨率对位姿估算精度的影响

从图6可见，像素分辨率越高，迭代和非迭代算法的针脚位姿估计精度都越高；总的来看，像素分辨率对迭代法估计精度的影响更明显。旋转视觉的针脚图像通过背光拍摄，图像对比度较高，因此针脚图像坐标的提取可获得较高的分辨率。

4)针脚个数：

如3.1节所分析，增加针脚元件针脚数量可增加式(7)方程的数量，这有助于提高旋转角的拟合精度，进而提升针脚位姿的估算精度。常见异形元件针脚数在2～8个左右，针脚数量更多的元件如PCI插槽等，元件本体较长，并且旋转拍摄时容易出现针脚遮挡的情况，因此不适合用旋转视觉检测定位。本小节针对2～8个针脚的元件，分析针脚位姿估计精度与针脚数量的关系，其它参数按照表1设置。

从图7可见，针脚个数越多，基于迭代的针脚位姿估计误差越小；图中非迭代算法的结果曲线，增加针脚数会导致定位误差变大，分析其原因为：新增针脚的旋转半径大，非迭代算法对旋转角误差没有修正作用，因此相同转角误差时大的半径所带来的针脚位姿估计误差也越大。

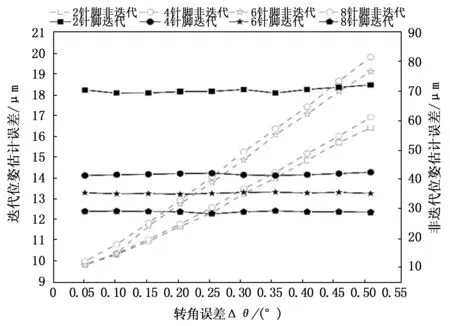
图7 针脚个数与针脚位姿估算精度关系

表1仿真参数和旋转角误差皆根据插件机实际工作参数而定，常见异形元件针脚数为2～8个，异形元件的插件误差通常要求不超过±0.05 mm，由图7可知， 其中2针脚元件的迭代位姿估计误差同比最大，但最大误差基本在±0.018 mm以内，可见本文所提出的迭代方法的针脚位姿估算精度完全能满足插件机的精度要求。

5)旋转取像点数：

本小节研究取像点数对位姿估算精度的影响，取像点数分别为4、6、8、12，旋转角均匀分布在圆周上，其它参数按照表1设置。

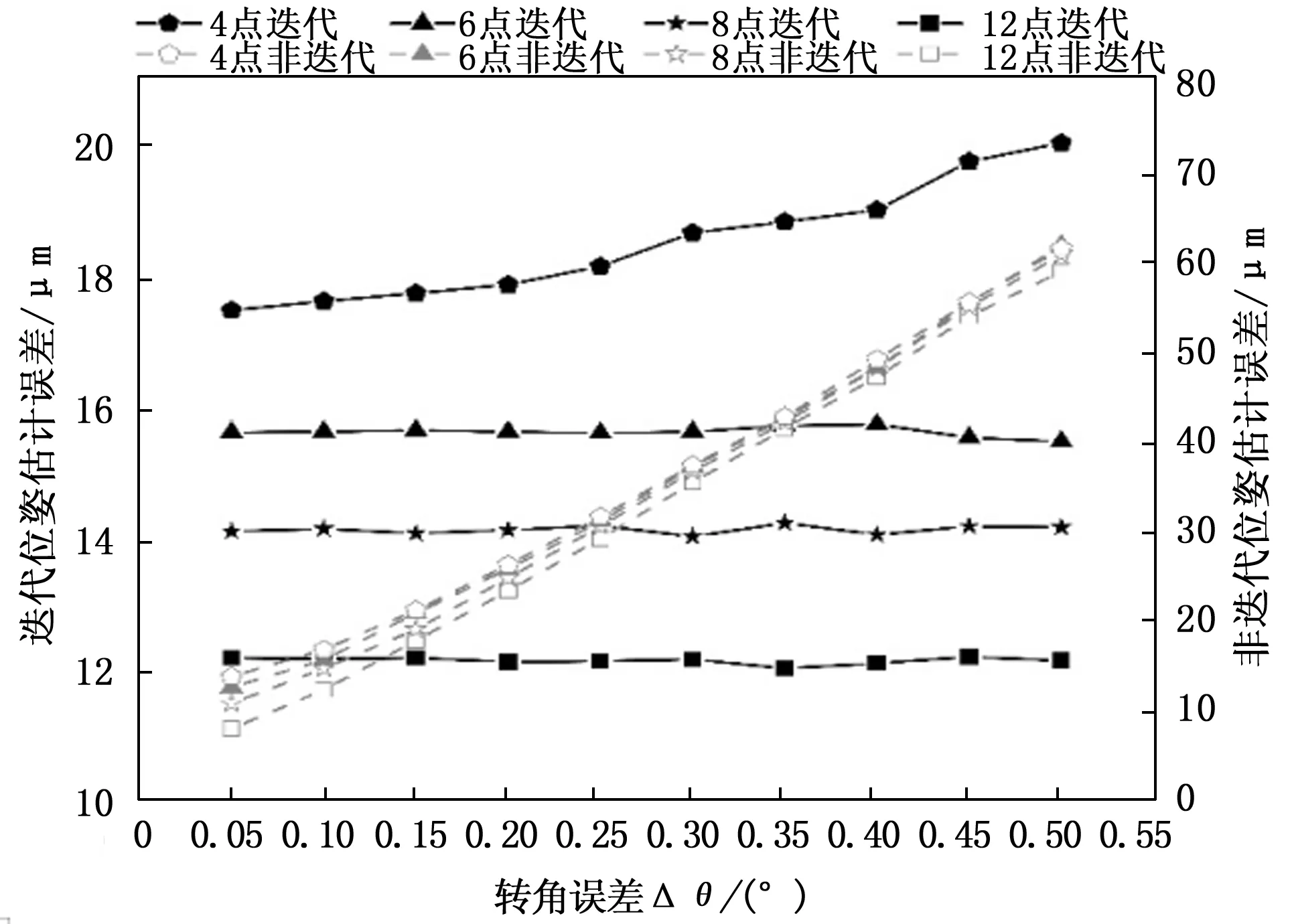
图8 取像点数与针脚位姿估计精度关系

由图8可见，取像点数越多，基于迭代的针脚位姿估计精度越高，这是因为增加旋转取像次数同样可增加式(7)方程的数量，因而有助于提高旋转角的拟合精度，进而降低位姿估算误差；但多的取像点数也是增大测量耗时的主要因素，因此需平衡取像点数与检测效率之间的关系，目前常用的取像点数为8点；此外，增加取像次数也有助于非迭代算法降低位姿估计误差，但因为该算法没有修正旋转角误差，因而其估算误差随转角误差增加而增加。

3.2 效率分析

为了验证本文针脚位姿估计优化方法的实时性，在配置为CPU i7-8550U、4.00 GHz、8 GB内存的计算机上用Matlab2020a的时间探查器分析计算效率。除了迭代次数和阈值外，影响迭代耗时的主要因素是针脚数和旋转取像点数，本小节针对常用针脚个数和取像点数分析本文优化方法的实时性。针脚个数分别取2、4、6、8，旋转取样点数分别取3、4、6、8、12，其它参数按照表1设置，算法平均耗时如表2所示。

表2 不同条件下优化方法耗时表

从表2中可见，算法的耗时与针脚数量、取像点数基本正相关。目前异形元件插件机每轮插4～6个元件，平均每个元件耗时500～800 ms。插件头从取件位移动至插件位一般需要350～400 ms，移动过程中同步进行旋转图像采集、针脚图像提取和位姿计算。从开始采集到完成针脚图像提取一般需要200 ms左右；插件一般都是逐个进行，因此第一个元件的针脚位姿估算至少有100 ms左右的处理时间。从表2可见，除了最高耗时135.80 ms的组合外，其它组合都能满足首个元件的插件实时性要求，在常见2～8针脚元件以及取像点中，最高耗时也少于65 ms；插装一个元件需要200 ms左右，因此随后插装的几个元件，表中的所有组合都能满足效率要求。

根据以上的仿真结果可得到如下结论： (1) 迭代法确实可降低因同步带传动带来的旋转角定位误差对位姿估计精度的影响；(2)图像噪声越小迭代法的位姿估算精度越高；(3)针脚个数或取像点数越多，迭代算法的估算精度越高；(4)像素分辨率越高，迭代法的针脚位姿估计精度越好；提高像素分辨率，可以改善图像噪声大而转角误差较小时迭代法的位姿估算精度。

由于篇幅限制，上述数据主要根据表1参数配置得到的。将表1的元件针脚坐标理论值和旋转角，换为其它元件针脚坐标或旋转角度组合(旋转半径在25 mm以内，组合的角度差异一般要求20°以上)，得到的数据与以上仿真结果类似。

4 结束语

本文在前期研究基础上，针对因旋转角误差影响针脚位姿估计精度的问题，提出一种基于位置约束和迭代拟合的元件针脚位姿估计精度优化方法。该方法利用元件针脚位置固定的约束关系，将圆拟合与旋转角拟合相结合，通过迭代实现了针脚位姿精密估计；理论分析和仿真结果都表明，该方法的精度和实时性均能满足异形插件的要求，本文研究为新款异形插件机因同步带传动引起的针脚位姿测量精度问题，提供了可行的解决方案。