“三问”——让数学思维向纵深发展
许敬
[摘 要]发展学生的逆向思维一直是教师追求的核心目标。在实现这一目标的过程中,教师可以引导学生将“倒过来推想”理解为:从情境现有的状态和经历的过程出发,去倒推之前的状态,即逆向思考,也就是要知道一个物体原来有多少的问题,必须要知道这个物体现在的状态和经历的变化过程。
[关键词]问题;倒推;逆向思考
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2022)08-0042-03
我们常常会被公开课中展现的“流畅”所迷惑。如,在我校的公开课“解决问题的策略——倒推”中,课堂上出现了一个共性的现象:教师自始至终都按照事先设计好的思路“牵着学生的鼻子走”,即便到了要放手让学生自主去探究的环节,依然不忘要引导学生几句;在问题抛出后,只要有小部分学生能够答出预设的知识点,教师就理所当然地认为全部学生都懂了,马上进入下一个环节。在这样流畅自然的课堂中,那些没有发言的学生真的听懂了吗?他们在思考的过程中遇到了哪些障碍?与此同时,那些发言的学生答出预设的知识点之后,是否都真正理解了?这些潜在的、有价值的问题往往随着下课铃声的响起,就再也没人过问了。
那么,究竟该如何做,才能让学生的数学思维在课堂教学中向纵深处发展呢?笔者将上述“流畅”的教学设计过程进行了舍弃,重新从本课的教学主体出发,采用“三问”的教学方式:1.启问,创设合适的情境,引导学生自觉思考“为什么要用倒推的策略”;2.追问,通过在新知的探究过程中,对学生进行抽丝剥茧式的追问,让学生在解决问题的过程中真正感受“怎样的情境才需要用倒推的策略来解决”,认识到此类问题的本质特征;3.自问,在新知建构的各个环节中合理设计反思、比较环节,让学生在自问中思考,使数学思维真正向纵深处发展。
基于以上“三问”,笔者重新确定本课的教学目标:第一,使学生认识倒推问题的特点,学会用倒推的思维分析问题,并确定解决问题的思路,最终根据问题的特点采用具体的倒推方法来解决问题;第二,使学生经历用倒推策略解决问题,丰富倒推策略的体验过程,感受倒推的知识与方法之间的联系,从而体会倒推这种逆向思维的好处,积累数学活动的基本经验,发展思维的灵活、敏捷等品质;第三,使学生在经历用倒推策略解题的过程中,感受倒推策略的应用价值,培养克服困难、学好数学的信心。同时,笔者还将本课的教学重点改为理解和认识倒推策略,将教学难点改为根据题目条件找到能够应用倒推策略的方法,并确定具体的解题步骤。
在观摩了多位教师的倒推策略主题教学之后,笔者从学生的实际出发,对之前的教学过程进行了调整和重新设计,现将再次执教这节课的过程整理如下。
一、情境导入,让启问引发学生思考
出示问题:今天天气特别热,李明在放学的路上买了一个冰激凌,此时他的口袋里还剩15元,想知道他的口袋里原来有多少钱,缺什么条件呢?
师:要想知道李明的口袋里原来有多少钱,不仅要知道现在的情况,还要知道原来口袋里的钱经历了哪些变化。(板书:买冰激凌花掉了5元)现在,你知道李明的口袋里原来有多少钱了吗?
生1:原来有5+15=20(元)。
师(追问):明明“花掉了5元”,为什么还用加法计算?
生2:因为花掉的5元是这笔钱原有的一部分。
生3:因为求原来的钱数,就要把花掉的钱还回去,所以要用加法。
师:请大家在头脑中想象一下问题情境的变化过程——原来有一些钱,花掉了一部分,剩下一部分,要求原来有多少钱,实际就是要将花掉的钱——
生(齐):再放回口袋里。
【设计构想】策略的形成,一定是学生在充分体验解题过程的基础上,发现这类问题的特点,从而激活已有的经验来获得相应的解决办法。本节课一开始,笔者以学生熟悉的“求口袋里原来有多少钱”为素材,出示一个缺少信息的问题,引发学生对钱数变化的关注。该设计属于“三问”中的启问环节,让学生自觉进入思考的场域,同时题目的设计考虑到了用倒推策略来解决的问题所具有的典型特征:结果是怎样的,经过了怎样的变化过程,最终求的是最初的状态。使学生在明确特点的基础上,自动抽象出数学模型。接着,笔者通过追问,引导学生理解“求口袋里原来有多少钱”就是要将花掉的钱还回去,让学生在简单、熟悉的生活场景中初步体验倒推的策略,为广泛、灵活地应用倒推策略解决问题奠定基礎。
二、自主探究,让追问深化探究过程
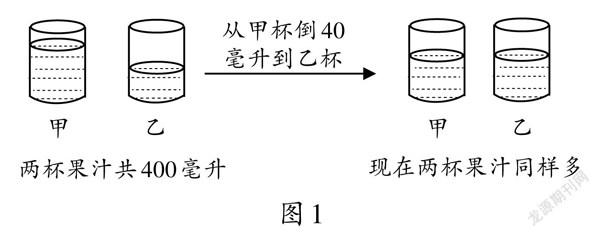
出示问题1:今天,王芳和萧桐来到李明家做客,李明家有一多一少两杯果汁,共400毫升。如果用这一多一少的两杯果汁招待两位客人,合适吗?聪明的李明从甲杯里倒40毫升果汁到乙杯里,这时两杯果汁就同样多了。(出示图1)
师:仔细看图1,你能提出哪些问题?
生1:现在甲、乙两杯果汁各有多少毫升?
生2:原来甲、乙两杯果汁各有多少毫升?
师:请大家以这两个问题为线索,先独立思考,有想法后再尝试在小组内讨论,必要时也可以通过画图、列表等策略来帮助自己厘清思路。(给学生提供尽可能多的表达方式,从而发散学生的思维)
师:哪个小组来汇报你们讨论的结果?
生3:因为400÷2=200(毫升),所以现在甲、乙两杯果汁各有200毫升。
师(追问):为什么要用除法计算呢?
生3:因为这时候两杯果汁是同样多的。
师:那么“原来甲、乙两杯果汁各有多少毫升”又该如何求呢?
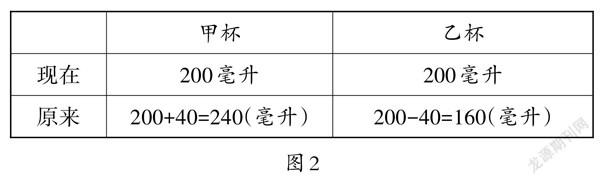
生4:可以用列表的方式。(如图2)
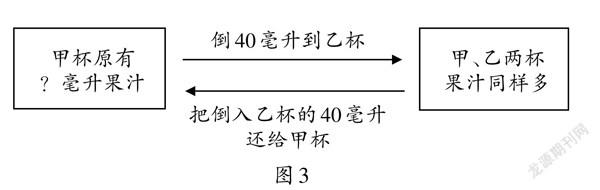
生5:也可以用画图的方式。(如图3)
(教师结合学生的发言,用动画演示将倒入乙杯的40毫升果汁倒还给甲杯的过程)
师:根据这样的倒推过程,你能列式计算吗?
生6:能。现在甲、乙两杯果汁各有400÷2=200(毫升),那么甲杯原来有200+40=240(毫升),乙杯原来有200-40=160(毫升)。
师:求原来有多少果汁,都是从哪里入手的?从现在的果汁怎么能得到原来的果汁?(板书:现在[]原来)
师:今天这节课,我们就重点来探讨像上面这样从结果出发,根据题中的变化步骤一步一步倒过来思考的策略——倒过来推想,也就是我们数学中常说的倒推、还原。(板书:倒推、还原)
【设计构想】教学任何解决问题的策略,都不能仅靠教师去讲授,而应是让学生在经历抽丝剥茧的过程中找到解题方法,由内而外获得真实感受和体验,这样的思维过程更清晰,学生对解题步骤的感知也更明确。与此同时,不同题目情境的复杂性不一样,学生在面对复杂问题时,会出现对题干信息处理不全面,解题思路不明朗的情况,而追问环节的设计则起到了引导的作用,让学生的探究和建构过程清晰可见。
出示问题2:赵蕾原来有一些邮票,又收集了35枚,发现部分与之前搜集的有重复,就送给了钟晴20枚,最后还剩下64枚。求赵蕾原来有多少枚邮票?
师:这个问题与刚才的情境相比,有什么不同?
生7:信息变多了,而且数量之间的关系没有刚才图示的那样直观。
师:你打算怎样处理题目中的条件,使问题看起来更加直观、简洁?
(教师根据学生的回答写出流程:赵蕾原有?枚→得到35枚→送出20枚→现有64枚)
师:要求赵蕾原来有多少枚邮票,可以从哪里开始思考?
生8:把变化的过程还原回去。
三、比较反思,让自问触及知识本质
师:刚才我们研究了关于求钱数、倒果汁和集邮这样三个用倒推策略解决的实际问题,谁能说说这三个问题有什么异同点?
生9:求钱数和倒果汁的问题信息量相对较少,条件之间的数量关系也比较简单,解决起来相对容易。
生10:集邮问题的信息量比较大,条件之间的关系较复杂,理解时存在一定的难度。
师:这三个问题的解决思路有什么一样的地方?
生11:都是从现在出发,运用倒推的策略解决。
生12:结果都可以用正推的方法来加以验证。
师:需要运用倒推的策略来解决的实际问题,有什么典型的特征?
生13:不论是哪个情境,其典型特征都是在知道事物经历了怎样的变化过程和现有结果的基础上,求原来的状态。
【设计构想】本节课在教学的多个环节中设计了及时的自问,让学生去回顾、比较、反思不同情境下,用倒推策略解决问题所具有的共同点,使学生能够站在一定的高度真正地去触摸倒推策略的实质,慢慢养成缜密的数学思维,提高数学思考的能力。
四、联系生活,让倒推策略发挥作用
出示问题1:王芳每天起床穿衣服要用10分钟,吃早饭要用15分钟,步行去学校要用20分钟,她需要在8:00前抵达学校,那么王芳每天早上最迟什么时候起床?
师:要解决这个问题,你准备从哪里开始思考,打算运用什么策略?
出示问题2:花果山上有棵蟠桃树,孙悟空天天来这棵树上摘桃吃,第一天吃了树上的一半多1个桃,第二天又吃了树上剩下的一半多1个桃,最后树上还剩下17个桃,这棵蟠桃树上原来有多少个桃?
师:请你尝试用不同的方法來解,并比较用倒推策略解题的方法,看哪一种更有优势。
出示问题3:星期天,李强和王芳相约一起去郊游,出发时他们乘坐的1路公交车上有48人,到图书馆站下车11人,到少年宫站上车15人,这时1路公交车上有多少人?
出示问题4:星期天,李强和王芳相约一起去郊游,出发时他们乘坐的1路公交车上原来有一些人,到图书馆站下车11人,到少年宫站上车15人,现在车上还剩52人,他们出发时1路公交车上有多少人?
师:问题3和问题4两个情境的特征有什么不同?什么样的情况下需要用倒推的策略来解决?
五、回归反思,提升对倒推策略的认识
通过对本课的设计,笔者逐渐意识到,策略单元的教学如果不能让学生真正地认识情境的特征,明确解题的思路,那么是无法让他们真正做到触摸知识本质的。那么,如何在教学中让学生认识情境特征,明确解题思路呢?笔者将方法总结为以下三点。
一是通过创设合适的情境,设计具有挑战性的启问,让思考成为可能。从本课的教学设计思路和具体安排可以看到,开头通过求钱数这一生活化的情境创设,引发学生自觉进入思考:要想解决原来有多少钱,必须怎么样?在研讨时,将“倒过来推想”分解为思维方式的逆向思考和具体运算的逆向运算两层含义。笔者基于这样的思考进行教学设计,真正做到了良好的开端是成功的一半。二是通过在学生合作探究的过程中,恰到好处地设计追问,让学生的思维向深处发展。本课将倒推策略的相关内容“镶嵌”在倒果汁和集邮这两个情境中,通过一系列追问的实施,让学生的思维不是仅仅停留在表面,而是沉下去找到需要用倒推策略解决的问题的本质特征,从中感知策略、认识策略,最终深化策略。三是通过安排适时的自问,让联结知识的本质浮现出来,为综合应用各种策略解决问题打下坚实基础。学生在经历自主探究之后,能够适时自问,问学到的知识,问掌握的方法,问如何进行思考,还会问今天这节课获得了怎样的经验和体会。如此,学生便能在策略意识形成的过程中继续成长。
总之,教学设计的出发点是以学生为主体,通过创设合适的情境,为学生提供自觉思考的空间和时间。通过教师的追问和引导,学生在自主建构知识的过程中,思维不再浮于表面,而是向下去探寻问题更为普遍的共性特征。最后,让学生通过及时的自问来形成核心思维,从而真正做到举一反三、触类旁通。
(责编 李琪琦)

