基于改进N-K 模型的铁路工程质量风险因素耦合效应分析
莫俊文,李 甲
(兰州交通大学土木工程学院,甘肃兰州 730070)
1 研究背景
铁路工程关系国计民生。近年来我国铁路项目的建设力度日益加大,《新时代交通强国铁路先行规划纲要》也明确提出了完善质量管理体系、确保工程质量安全的要求。在建设过程中,铁路工程质量易受到来自人员、材料、环境、设备、管理等多种风险因素的影响,如何对风险因素进行有效控制成为学者研究的重点,如唐秋宇等[1]对风险影响因素的综合重要度进行排序,找出川藏铁路雅林段工程建设质量管控重点;卢睿等[2]基于贝叶斯网络对风险因素的敏感性分析与逆向推理,提出了铁路四电工程质量安全三维管理体系;Kuo[3]等利用网络理论,以风险因素作为节点、因素间相互影响关系作为传递路径,建立地铁施工事故网络并找出关键风险因素和风险传递路径。既有的质量风险研究大多采用独立量化各风险因素的风险值来确定工程整体风险等级的风险评价模式,然而在实际的铁路工程施工系统中存在着多个风险影响因素,各风险因素不仅会单独作用,更会在传递过程中发生交叉耦合,使得原风险扩大或产生新的风险。因此,在分析风险的发生机理时,不仅要对单个风险因素进行分析,还要考虑到风险因素之间出现交叉耦合,分析因素的耦合性并对耦合作用强度进行度量。而现有的风险因素耦合效应研究大多集中于交通运输和煤矿等领域,例如黄文成等[4]基于“触发器”概念分析铁路危险品运输系统耦合风险因素的形成机理,认为安全事故的发生取决于因素风险耦合值大小;乔万冠[5]运用系统动力学对煤矿事故风险因素耦合值进行度量,发现人与管理因素在风险因素耦合中参与最多。在工程领域中,Fang 等[6]提出了城市群城市化与生态环境的互动耦合理论和时空动态耦合模型,用于促进大城市群的可持续发展;周红波等[7]将复杂网络与N-K 模型相结合,探讨了塔吊安全风险事故的来源和路径;Yang 等[8]开发了基于社交网络分析的风险分析方法用于评估复杂绿色建筑项目中的风险及其相互作用。
通过分析文献可以发现,现有相关铁路工程质量风险因素耦合的研究较少,且绝大部分没有考虑二级子因素之间的耦合效应对风险总水平值的影响。因此,在现有的研究基础上,笔者基于参与地区科学基金项目的研究,采用N-K 模型,结合系统动力学模型定量计算影响我国铁路工程质量风险的因素耦合值。N-K 模型是 Kauffman[9]提出的一个解决复杂问题的通用模型,它主要用于分析系统内部各个要素间的相互作用对系统整体产生的影响,但是N-K 模型只能计算当前主因素之间的耦合值,不能动态预测因素的耦合关系变化对系统风险的影响程度,而系统动力学模型恰好可以通过对复杂系统进行动态预测来剖析系统中各因素之间的相互影响关系,因此本研究选择利用系统动力学模型对N-K 模型进行改进,建立铁路工程质量风险动态耦合分析模型。改进后的模型从耦合作用的角度对影响铁路工程质量的风险因素展开研究,通过计算不同耦合方式下的主因素风险耦合值,并对子因素之间耦合值变化对风险系统的影响进行仿真模拟,动态预测风险耦合关系变化对未来风险的影响,以探明对铁路工程质量风险管理影响最大的风险因素耦合组合,找出风险系统的关键脆弱部位并针对结果提出相应的控制措施,为铁路工程质量风险管理和防范提供决策依据和理论支撑。
2 风险因素耦合分析
2.1 风险因素识别
按照风险识别流程,采用人员(man)、设备(machine)、环境(medium)、管理(management)的4M 系统理论并参考李梦晨等[10]、Taheri 等[11]和夏铭[12]的研究,秉持清晰全面、便于计算的原则,将铁路施工质量风险管理系统分为4 个主因素以及17 个二级子因素(见图1)。
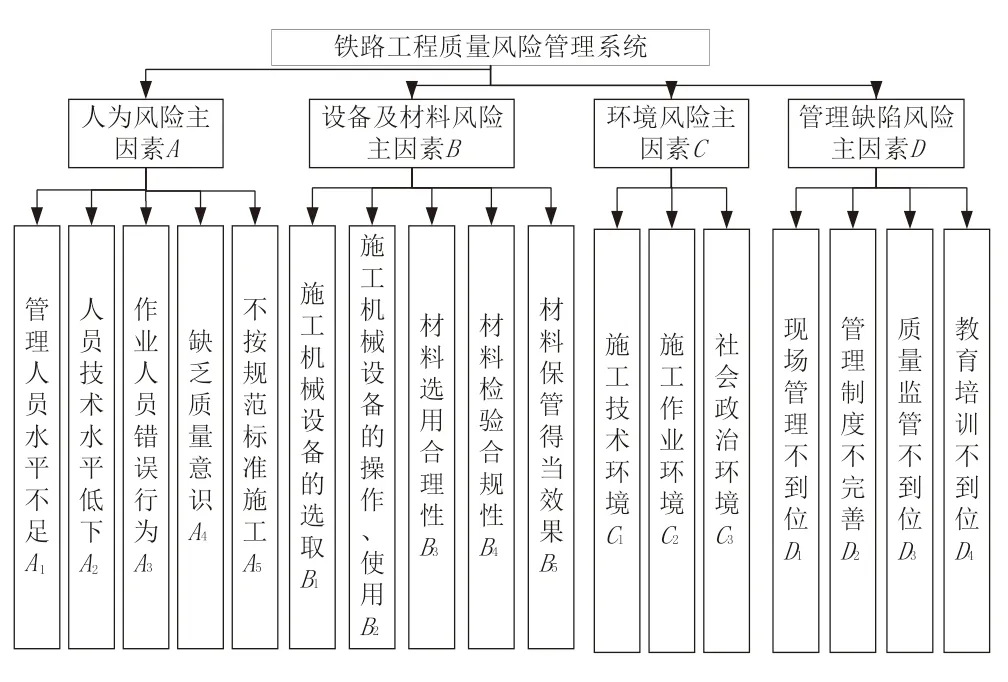
图1 铁路工程质量风险因素识别结果
2.2 风险因素耦合机理分析
“耦合”这一概念源于物理学,表示两种或两种以上的系统或运动形式通过相互影响、相互作用彼此趋于协同的现象[13]。铁路工程质量风险因素耦合过程如图2 所示。

图2 铁路工程质量风险因素耦合过程
参考黄文成等[4]、乔万冠[5]、杨婷等[14]、付邦稳等[15]的研究,将铁路工程质量风险因素耦合分为以下3 类:
(1)单因素耦合风险,指主因素自身包含的风险子因素之间发生的耦合作用。
(2)双因素耦合风险,指影响铁路工程施工安全的两个风险主因素间的耦合作用。以a、b、c、d分别代指人为风险、设备及材料风险、环境风险、管理缺陷风险,耦合值分别记为
(3)多因素耦合风险,指影响铁路工程施工质量的3 个及以上主风险因素间的耦合作用。其中,三因素风险耦合值分别记为四因素风险耦合值记为T(a,b,c,d)。
3 风险因素耦合度量模型
3.1 N-K 模型
N-K 模型可以通过统计某种耦合方式发生的概率来计算风险子系统之间的交互信息[12]。其中,T值表明耦合作用对发生质量风险可能性的影响程度,T值越大即质量风险越大。参照Kauffman[9]的研究,N-K 模型包含2 个参数:N为构成系统中因素的个数;K为因素之间存在的相互耦合关系的个数。如果系统中有N个因素,每个因素有v种不同状态,则系统因素耦合方式有vk种;当K达到一定程度的时候,系统因素耦合关系组合起来便可形成网络,K的取值范围为计算公式如下:

式(1)~(11)中:“*”表示该因素处于未知状态;为人在第h种状态、设备及材料在第i种状态、环境在j种状态、管理在第k种状态下4 种因素风险耦合发生的概率。
3.2 系统动力学模型
由于N-K 模型无法对由耦合关系变化造成的影响进行动态预测,因此参考刘熠林[16]、姜盛玉等[17]和Yang 等[18]的研究,采用系统动力学方法改进N-K模型,以人为和管理(以下简称“人-管”)风险因素耦合为例,对两主因素下的子因素耦合情况进行仿真模拟,通过调节不同耦合因素组合之间的耦合值来观察一定时期内人-管风险因素耦合系统的风险总水平变化趋势,筛选出影响人-管风险系统风险水平变化的关键耦合因素组合。如图3 所示。

图3 铁路工程质量人-管风险因素因果关系
4 实证分析
4.1 N-K 模型计算主因素耦合度
2019 年1 月—2020 年8 月,国家铁路局官方网站共通报事故调查处理结果和行政公开处罚信息132起(以下简称“样本工程事件”),整理所得不同耦合方式导致事故发生的次数p和频率P如表1 所示。

表1 2019 年1 月—2020 年8 月我国铁路事故统计
要想计算各风险因素耦合作用后产生的风险T值,首先需得确定条件下样本工程事件中单因素、双因素和多因素发生概率,以为例,其计算过程如式(12)~(14)所示。


同理可得剩余单因素、双因素和多因素确定条件下发生概率(如表2 所示)。

表2 确定条件下样本工程事件中风险因素的耦合概率
根据表2 以及式(1)~(11),可以计算出不同风险因素耦合方式下的耦合风险值T,计算结果见表3。

表3 样本工程事件中风险因素的耦合值
4.2 人-管因素耦合系统动力学模型仿真
在进行数据统计时,人-管因素出现耦合的概率最大,根据Frank Bird 在海因里希事故因果连锁理论的基础上提出的现代事故因果连锁理论,尽管人的不安全行为导致事故的重要原因,但认真追究事故的根本原因是管理失误[19],因此选择人-管风险因素耦合系统为本次仿真对象,利用Vensim PLE 软件进行仿真模拟,仿真边界是一个完整的铁路工程质量风险管理系统中的人为因素子系统和管理因素的子系统。模型仿真的时间边界为24 个月,运行步长为1 个月。系统流图如图4 所示。其中,L表示人-管系统因素耦合风险水平总值;L(A)表示人为因素风险水平,L(D)表示管理缺陷风险水平,L(mn)表示人-管风险因素子系统第m类风险因素的第n个指标的风险水平;R(A)表示人为因素风险水平变化量,R(D)表示管理缺陷风险水平变化量,R(mn)表示第m类风险因素的第n个指标的风险水平变化量;表示第m类风险因素的第n个指标与第类风险因素的第 个指标之间的风险耦合值。其中

图4 样本工程事件人-管风险因素存量流量图
在进行仿真前,首先要确定9 个二级子因素之间的耦合值及权重,利用层次分析法(AHP)确定权重,然后参考夏铭[12]的研究,利用多层次灰色评价方法计算各因素的耦合值。
铁路工程人-管风险子因素对铁路工程质量风险的功效函数的表达式如下:

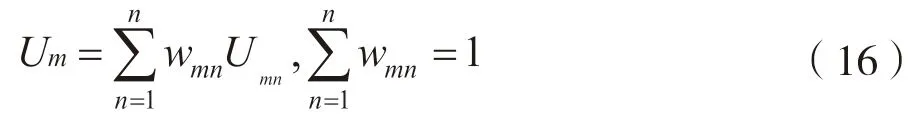
灰色评价模型的数字特征计算结果如表4所示。

表4 样本工程事件风险因素灰色评价模型的数字特征
根据对功效函数的分析,假设一个系统中子系统的个数为s,那么第m个与第m'个子系统两两耦合的耦合度模型可以表述如下:

根据功效系数和因果回路图依次计算人-管系统子因素两两耦合的耦合值,结果如表5 所示。

表5 样本工程事件中风险变量取值
将表5 中计算所得数据代入系统动力学模型进行仿真模拟,可以得到24 个月内人-管系统因素耦合风险水平总值L的变化趋势如图5 所示。从图5可以看出,在风险耦合作用下,风险的增长速度与水平值随时间增加而增加,在第24 个月,系统的风险总水平值达到71.183 9。

图5 样本工程事件人-管系统因素耦合风险水平总值的时间变化
根据海希里因的事故因果连锁理论,事故的发生过程如同推倒多米诺骨牌,抽出一张牌即可破除事故链从而达到防止事故发生的目的[20],因而在实际操作过程中完全避免某一风险因素是几乎不可能的,但降低风险因素之间的耦合值就如同拉开骨牌之间的距离,可以减少事故发生。为了确定风险因素两两耦合的耦合值发生变化对总风险水平的影响程度,将11 个耦合组合的耦合值各减少20%,再次模拟计算24 个月内的风险总水平值,观察风险总水平值变化情况,变化值越大则对应因素发生耦合对总风险影响越大。模拟结果如表6 所示。
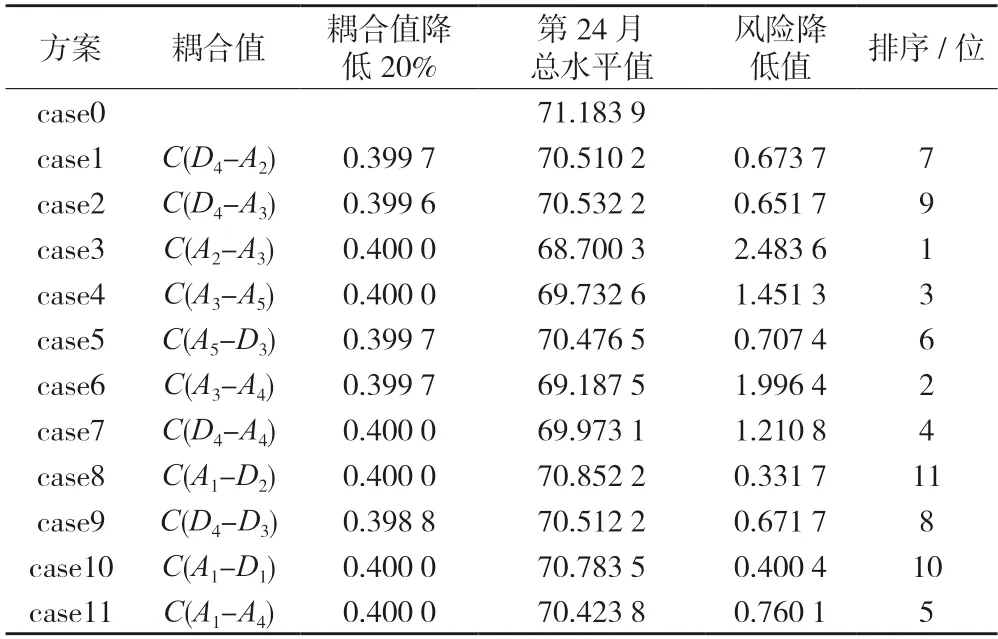
表6 样本工程事件风险总水平值变化情况
5 结论
铁路工程质量风险管理系统受人员、设备、材料、环境、管理等多个主要影响因素的耦合效应影响,本研究构建了N-K 模型与SD 模型相结合的新型风险因素耦合效应分析模型,梳理因素之间的耦合关系,量化风险要素耦合效应的危险程度。从实证计算结果可知,耦合值的大小基本与参与耦合的风险因素数量成正比,而质量风险事故发生概率与耦合值正相关,耦合值越大则发生质量风险事故的可能性就越高。在N-K 模型计算的T值中,有风险A和风险D参与的双因素和多因素耦合时T值均较高,其中在双因素耦合中,T25明显高于其他双因素耦合模式,说明风险B和风险D之间存在着较大的耦合性,一旦出现耦合则风险发生的概率较大。SD 模型仿真模拟结果表明,耦合值降低会使人-管系统风险水平总值降低,同时也会降低风险增加的速度,因此,识别关键风险耦合因素组合和降低风险因素之间的耦合值是控制风险增长速度的有效办法。
综合来看,在实际施工过程中,首先要加强对原材料和设备的管理,对二者进行严格检测,风险管理人员应结合工程项目的布置、施工现场条件、施工程序和施工工艺,控制设备及材料的选择、检验、使用和维护,降低两因素之间的耦合效应以保障工程质量。其次要从人为风险因素着手,重点防范人员错误行为与其他风险因素发生耦合,例如可以通过岗前教育、讲习会、座谈会等形式让作业人员学习正确的作业方法,规范人员日常操作,提高技术水平;加强作业人员教育培训,通过“时时讲、天天讲”提高人员的责任感,由内驱动作业人员牢牢树立质量安全意识;对有违纪吸烟、饮酒上岗等行为的人员进行教育和适当处罚并督促整改,从源头防范错误行为的发生。最后建立定期质量风险管理检查制度,发现质量隐患及时反馈,要求落实整改时间,并对整改情况进行复查来降低风险因素之间的耦合度,进而降低风险总水平值。

