基于加权核范数和L2,1范数的最优均值线性分类器

曾德宇 梁泽逍 吴宗泽

(广东工业大学自动化学院 广州 510006)

(广东工业大学粤港澳离散制造智能化联合实验室 广州 510006)

1 引言

基于学习算法(包括机器学习[1]和深度学习[2,3])的缺陷检测方法是近年来工业检测和智能制造领域的热门研究方向。相对于需要大量数据样本以及较长的训练时间的深度学习而言，机器学习算法在小规模数据集上更具备分类的优势[4]。因此工业上更多的是采用机器学习的方式进行缺陷的分类[5]，如SVM(Support Vector Machine)算法[6,7]、特征选择[8]等。尽管大多数传统方法能够处理许多分类任务，但它们依赖数据的真实性和不受干扰。这意味着带有噪声的数据会严重降低算法的性能[9]，这是工业现场中的常见情况。针对上述问题，近些年提出了一系列鲁棒方法的研究。与传统线性回归算法中的标准向量内积不同，Chen等人[10]提出了一种新的线性回归算法，其修剪内积不会受到任意损坏点的太大影响。同样的，L2,1范数作为一种比L1范数更好的鲁棒惩罚度量被广泛应用于线性判别分析(Linear Discriminant Analysis, LDA)[11]，Fisher线性判别分析(FLDA)和稀疏鉴别分析(Sparse Discriminant Analysis, SDA)[12]来提高方法的鲁棒性。Wright等人[9]提出了一种将测试样本分解为训练集和稀疏噪声的稀疏表示的方法，并利用其稀疏表示进行分类。此外，还提出了许多基于统计的鲁棒方法[13,14]。

数据恢复和矩阵补全方法被提出来处理推荐系统和图像处理问题，并成为近年来的研究热点[15–17]。Candes等人[18]首先提出了鲁棒主成分分析(RPCA)，它利用低秩和稀疏约束来压缩噪声数据的秩并分离噪声。相似地，L2,1范数[19]也被用于改进RPCA模型从结构化稀疏噪声中恢复数据[20]。Nie等人[21,22]提出结合Schatten-p范数和Lp范数最小化代替核范数以及L1范数最小化作为低秩和稀疏约束的更好凸宽松。He 等人[23]利用最大相关熵准则的鲁棒性，提出了一种基于最大相关熵准则的鲁棒主成分分析模型。为解决数据恢复中的最优均值问题，一种最优均值鲁棒主成分分析模型被提出用于自动去除最优均值[24,25]。

最近的一些研究发现，数据的无监督结构学习可以有效提高识别和分类算法的性能和鲁棒性[26–29]。Goldberg等人[30]提出了一种转导矩阵补全模型来同时处理多标签学习、转导和缺失数据补全。通过样本特征矩阵和样本标签矩阵联合低秩的新假设，具有缺失数据的多标签转导学习问题可以通过其增广矩阵补全问题来处理。Cabral等人[31]提出了一种应用Hinge loss作为惩罚来提高鲁棒性的转导矩阵完成的发展，并成功应用于多标签图像分类。Huang等人[32]提出了一种RLDA方法，将鉴别学习模型与鲁棒数据恢复模型相结合，而不是仅仅作为一种预处理算法。Zeng等人[33]改进了RLDA方法，提出了加入带有标签信息的核范数最小化模型以提高RLDA方法在少量有标记样本数据集上的分类效果。与在LDA之前简单地运行RPCA不同，RLDA不仅通过恢复的低秩数据来学习分类器，而且还使用分类器来改进数据恢复的结果[34]。

但是，上面的RLDA方法忽略了数据的最优均值。虽然中心化或归一化的过程总是在计算之前完成，但是数据本身所受到的稀疏干扰(或称为在数据中的非高斯分布噪声)会影响数据的均值使得所观测到数据的均值并非数据的最优均值(亦或者中心)。均值的偏移会使得数据在秩最小化过程中随着稀疏噪声从数据中抽取出来，数据均值也会产生变化[24]。秩最小化凸关系的核范数总是压缩数据的几个主要成分，从而消除了数据的一些局部信息。此外，几项工作表明，基于L2,1范数的目标函数对数据点中的异常值具有鲁棒性[11,19,20]，并且L2,1范数正则化选择具有联合稀疏性的所有数据点的特征。基于以上这些工作和假设，本文提出了一种新的鲁棒线性判别分析方法，称为最优均值鲁棒线性判别分析(Optimal Mean Robust Linear Discriminant Analysis, OMRLDA)。本文的主要贡献总结如下：

(1) 首次关注带有稀疏噪声数据的分类问题中的均值偏移问题，提出最优均值的鲁棒线性分类器模型；

(2) 在鲁棒分类器模型中，首次引入加权核范数用于秩最小化代替核范数从而避免对主要成分的压缩，首次引入结构化稀疏的L2.1范数更好地进行噪声的分离；

(3) 提出采用交替方向乘子法将复杂的优化目标分解成几个子问题分别优化；

(4) 在具有不同比例损坏的标准数据集上实验证明本文方法比其他先进的方法表现更好。

本文的其余部分结构如下。第2节给出了一些重要的符号并简要回顾了LDA和RLDA。第3节通过L2,1范数和加权核范数最小化介绍了OMRLDA的算法。第4节给出了实验结果，显示了本文方法的性能。第5节给出结论和展望。

2 相关工作概述

2.1 符号

对于矩阵A∈Rm×n, aij表示这个矩阵第i行第j列的元素。aj,ai分别表示矩阵A的第j列和第i行。

对于向量v∈Rn，其L0范数，L1范数和L2范数

2.2 LDA

2.3 RLDA

子松弛为其凸宽松。问题式(7) 可以通过使用增广拉格朗日乘数 (Augmented Lagrange Multiplier,ALM) 方法来有效求解[35]。

值得注意的是鲁棒回归不等同于使用首先由RPCA处理的干净数据训练线性回归。鲁棒回归可以以受监督的方式从输入数据X=D+E中恢复干净的部分。因此，鲁棒回归的无噪声分量D可以保留X与Y最大相关的子空间。

3 基于加权核范数和L2,1范数的最优均值线性分类器

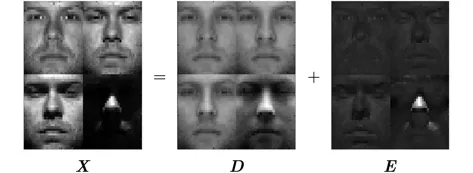
图1 改进模型

3.1 优化

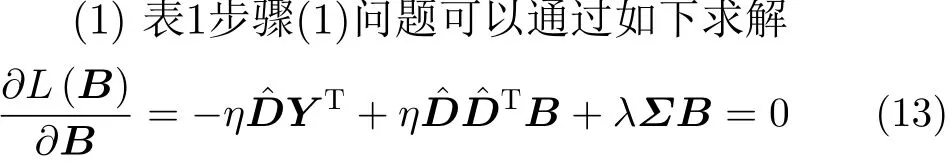
表1 基于交替方向乘子法求解问题式(12)

3.2 计算复杂度

为了估计本文提出的OMRLDA算法的复杂度，列出了算法的每次迭代运行条件，如表2所示。结果表明，该算法的总计算复杂度为O((dx+1)2n)或O(dxn2)。

表2 单次迭代计算复杂度分析

3.3 测试数据的鲁棒性

模型式(9)虽然能解决训练时候数据的噪声干扰问题，然后在测试时候，测试数据并非是干净的。于是，本文提出以下学习模型，将通过模型式(9)处理得到的干净数据D作为字典，学习测试数据Xte在字典D上的低秩表示Zt

同样地，模型式(22)可以写成其ALM形式并采用交替方向乘子法(ADMM)求解。

4 实验验证

在这部分，通过采用YaleB, AR与ORL共3个真实的分类数据集，其采样图片如图2、图3和图4所示。在数据集上加上0%～40%的噪声，采用5折交叉验证的方法，与k-NN, LR, SRC, SVM, RPCA+LR,RLDA[32]和BDLRR[39]7种方法进行比较。结果采用平均准确率±均方差的形式展示。

图2 YaleB 数据集的一些样本

图3 AR数据集的一些样本

图4 ORL数据集的一些样本

4.1 参数选择

每个实验的训练集是从每个数据集中随机选择的，剩下的样本用于测试。对于每个数据集选择50%的数据作为训练集，剩余的50%作为测试集，即训练集样本数和测试集样本数相同。本文实验通过

对于k-NN方法，参数k从1到10中选择。对于其他方法，参数从{10–5, 10–4, 10–3, 10–2,10–1, 1, 10,102, 103, 104, 105}中选择。

4.2 实验结果

实验结果如表3所示，其中，百分比表示噪声的比例，较大的值(%) 表示更好的性能，最佳结果以粗体显示。可以得出以下3个结论：随着数据损坏程度的增加，所有方法的准确性都会降低；RPCA不仅没有提高 LDA的准确性，反而降低了其性能；实验结果表明，OMRLDA在处理包含稀疏噪声的数据方面优于其他先进方法。

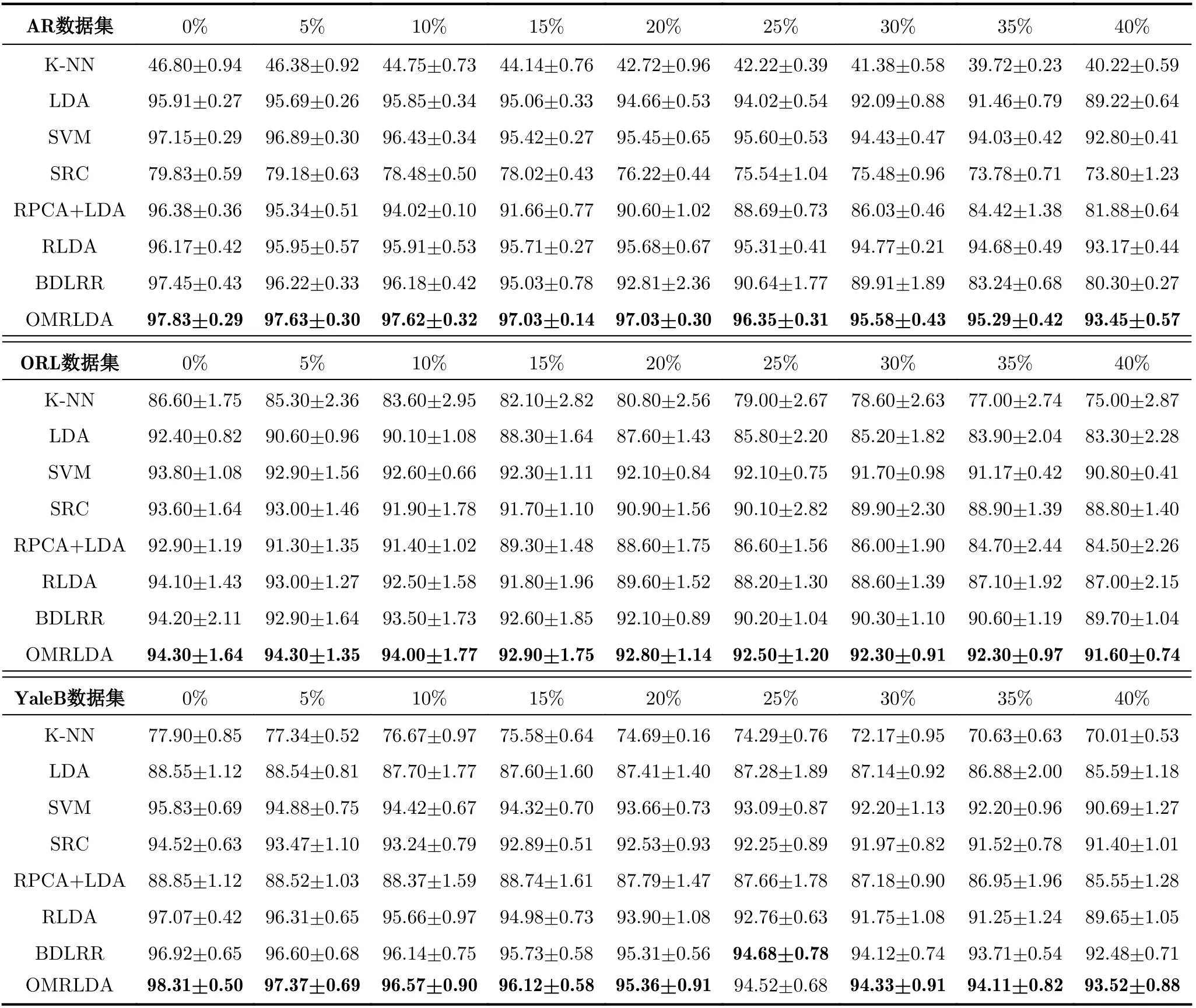
表3 各个算法在ORL数据集、AR 数据集和YaleB 数据集的识别率

4.3 不同参数的性能

本小节研究了两个超参数η和λ对本文算法性能的影响。实验是在具有25%随机稀疏噪声的 AR 数据集上进行的。图5为η和λ在具有25%随机稀疏噪声的AR数据集上的不同值的性能，可以看出，在λ ∈{ 10–1, 10–2, 10–3, 10–4,10–5}∩η ∈{1, 101, 102, 103,104, 105}，OMRLDA可以获得不错的性能。

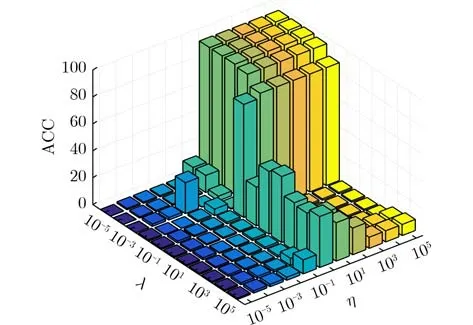
图5 η 和λ 的性能

5 结束语

在实际的工业检测和分类问题中，噪声和干扰是无法避免的问题。除了采用物理和人工方法尽可能免除前期噪声外，本文提出了一种新的OMRLDA模型，其在正则化和误差测量上具有L2,1范数最小化，旨在自动去除目标函数中的最优均值同时优化训练和测试时噪声对于学习算法的影响。应用ADMM方法对问题进行优化，给出每个子问题的解。实验结果表明本文的方法在一些最先进的方法中的优越性，例如SVM, SRC和RR。在未来的工作中，将研究其他一些非线性算法，例如逻辑回归和核方法，通过解决非线性分类方法和矩阵分解的结合模型，进一步提高算法的分类性能。