减摇鳍在零航速船舶减摇运动中的应用

许炀垲，梁玉珂，沈林维

（浙江大学海洋学院，浙江 舟山 316021）

0 引 言

随着海洋事业的发展，越来越多的舰船对低航速甚至零航速下作业呈现需求的趋势。普通减摇鳍因其升力机制影响无法在零航速下实现减摇，而不受船舶航速影响的减摇水舱存在占用船舶内部空间和排水量的劣势[1]，尤其是它的减摇效率存在不确定性。因此，如何减轻低航速下舰船的横摇运动是个亟待解决的问题。

2002年，Naiad和MARIN 首次联合提出了零航速减摇鳍，并通过试验发现该减摇系统的减摇效率达到63%～95%[2-3]。基于拍打翼的观察和研究，MARIN[4]提出了一种以弦长为转轴进行拍打的零航速减摇鳍，也称拍打鳍，并在与常规零航速减摇鳍模型的对比试验中发现，在恒定转矩下拍打鳍产生的冲量会高于常规鳍，所需的瞬时功率则低于常规鳍。Gaillarde[5]分析了零航速减摇鳍惯性力和粘性力的作用，以及鳍相对于船舶横摇的响应时间，发现减小鳍的展弦比有利于船舶作业。国内研究人员通过分析零航速减摇鳍的展弦比、翼梢形状等特征，针对其升力机制，提出了一种估计鳍基本尺度的方法[6]。

金鸿章等[7]对零航速减摇鳍进行了受力分析，将升力分解成形状力、旋涡力和附加质量力，发现鳍的升力与转动角速度、角加速度等因素相关。宋吉广[8]确定了零航速减摇鳍升力公式中的未知参数，其计算结果与试验值接近，为进一步研究零航速减摇鳍的升力机制提供了基础。叶青云[9]提出了计算零航速减摇鳍升力的经验公式，与CFD 方法得到的模拟值比较符合。Liang 等[10]基于径向基函数和回归神经网络进行了船模横摇试验和模拟，利用与波浪相关的相位匹配实现船舶减横摇，为零航速减摇鳍减摇方法提供了理论思路。

总之，国内外对零航速减摇鳍的研究已近20年，零航速减摇鳍几何模型建立方法已经基本成型；但在减摇机制上大部分是基于实际应用的控制策略研究[11]。本文将利用CFD 方法，在数值模拟减摇鳍简单运动的基础上，分析得到减摇鳍运动与船舶横摇运动之间的关系，最后利用减摇鳍的主动简谐运动，对零航速船模在4种规则波中的横摇运动进行直接数值模拟，获得减摇鳍的减摇效率。

1 控制方程

由于工程实际问题所涉及的流动复杂性，考虑到工程精度要求和计算发展现状，流动控制方程多会采用如下雷诺时均后的连续性方程和纳维-斯托克斯（RANS）方程：

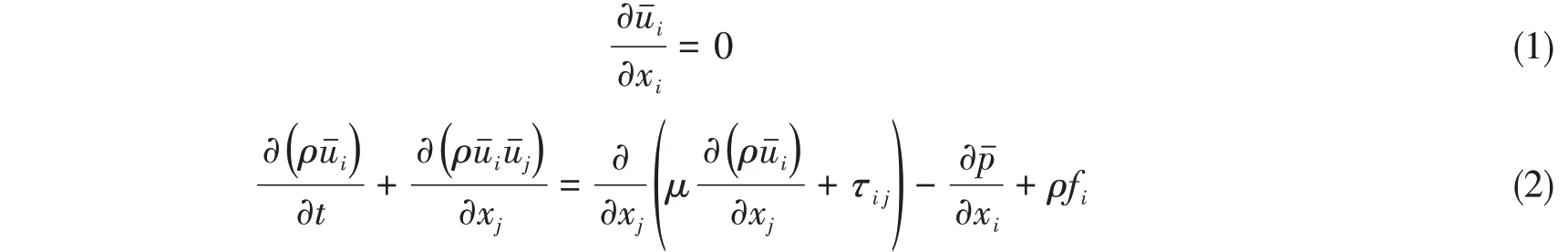
本文采用SSTk-ω湍流模型来计算雷诺应力。SSTk-ω湍流模型在处理近壁和远场流动时，分别采用类似标准的k-ω和k-ε湍流模型计算方式，从而较好地实现由内部低雷诺数到外部高雷诺数的过渡[12]。

2 运动减摇鳍的水动力模拟计算

零航速减摇鳍的运动可通过重叠网格技术实现。网格由背景区域和减摇鳍运动区域两部分组成，前者静止，后者随鳍作刚性运动，区域之间进行信息传递。为确保信息传递的连续和高效，鳍运动区域要求始终在背景区域内。本章对有航速和无航速两种情况下的鳍运动进行数值模拟和验证。

2.1 有航速的简谐运动

减摇鳍的具体模型及其运动形式如图1所示[13]：

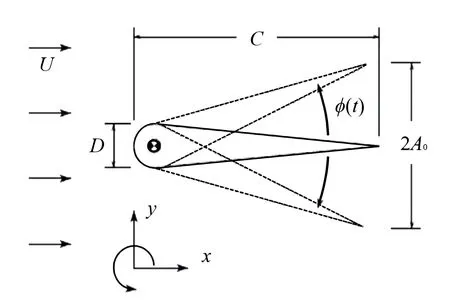
图1 翼型几何模型运动形式[13]Fig.1 Motion pattern[13]of airfoil model

均匀来流速度U=1.5 m/s,鳍围绕半圆形前缘的圆心进行简谐运动，旋转角度φ表示为

式中，φ0为鳍旋转的最大角度，sin（φ0）=12A0/11C，f为鳍旋转的频率。考察鳍模型的弦长C=1.2×10-2m，斯特劳哈尔数St=Df/U=0.22，AD=2A0/D=1.81，Re=UC/ν=440，ν为运动粘度系数，不考虑湍流的影响，采用二维模型。

图2 为计算区域和边界条件设置。左边为速度入口，右边为压力出口，顶部、底部及减摇鳍表面均设置为无滑移壁面。

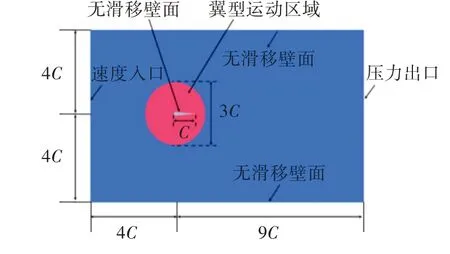
图2 计算域大小和边界条件Fig.2 Computational domain and boundary conditions

图3 为网格设置示意图，在鳍的运动区域附近设置两层网格加密区。第一层加密网格的尺寸为3.125×10-4m，第二层加密网格的尺寸为6.25×10-4m，最外层背景网格尺寸为1.25×10-3m，总网格数量为17万。取时间步长Δt=2.5×10-5s。

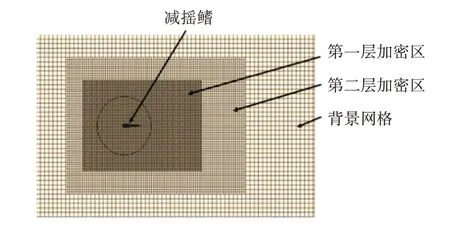
图3 网格加密情况Fig.3 Mesh encryption

将数值模拟获得的升阻力系数与Andersen等[13]文献中的试验值进行对比，结果如图4所示。二维模拟中，升力系数CL和阻力系数Cd的表达式分别为

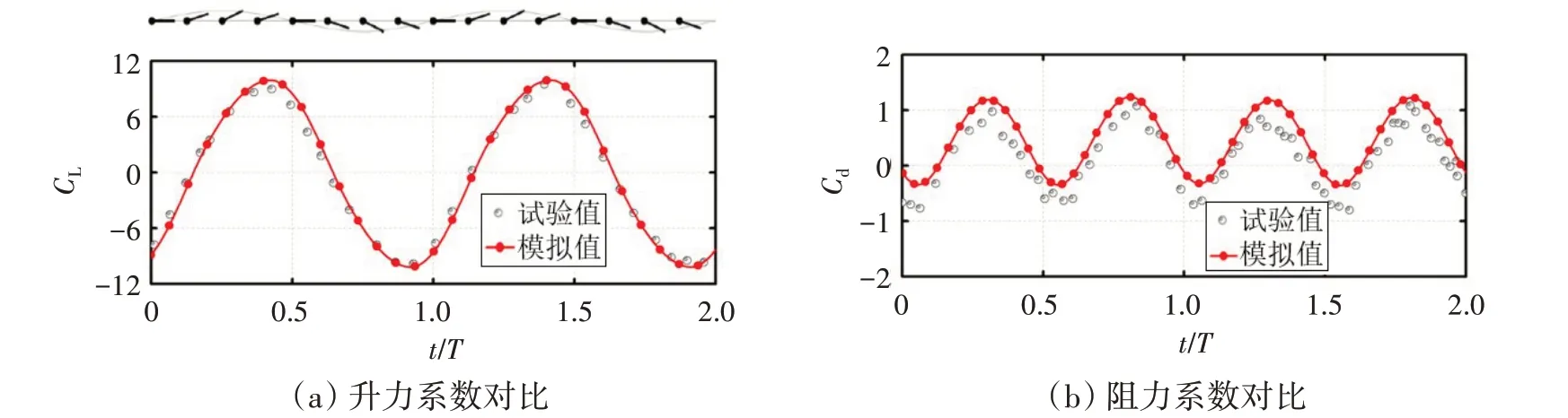
图4 升力系数和阻力系数模拟值和试验值的比较Fig.4 Comparison of simulated and tested values of lift and drag coefficients

式中，FL为鳍受到的升力，Fd为鳍受到的阻力。

可以发现，升力系数的模拟值与试验值非常接近，但阻力系数存在一定差异，这主要有两方面的原因。一方面，本计算模型是二维，而试验中采用的是三维模型；另一方面，升力系数主要由翼型上、下表面压力差所产生，而阻力系数受剪切应力的影响较大，后者对流动的分离及尾部流动更加敏感。

2.2 零航速简谐运动

采用茹可夫斯基翼型结构进行二维减摇鳍模拟，如图5所示，其中，d1是鳍轴和弦长中心之间的距离，C为弦长，S为展长，φ（t）为转动角度。本节考虑鳍弦长C=2.838 m，展长S为单位长度，d1=0.852 m，鳍作简谐运动如公式（3），φ0=π/6，f=1/8。

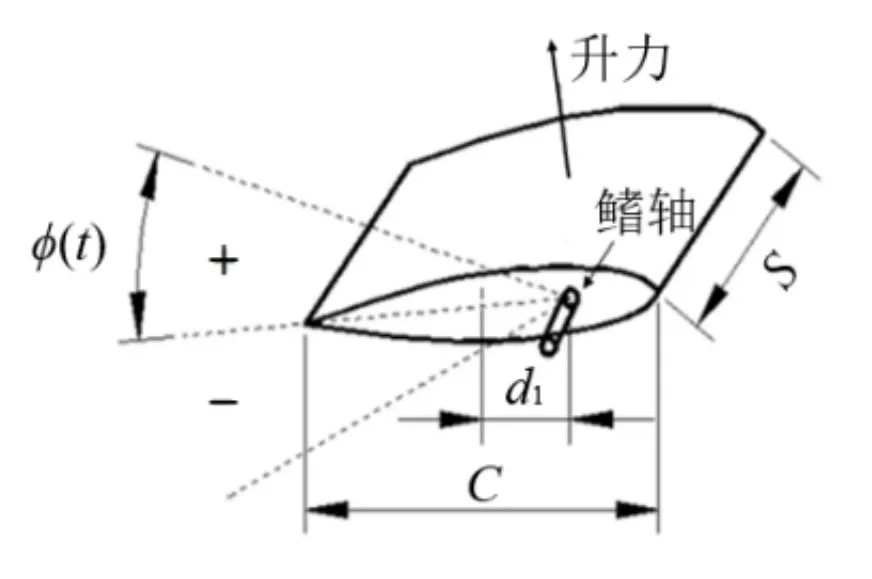
图5 翼型几何模型[8]Fig.5 Geometric model of airfoil

计算域及网格结构设置与有航速鳍的类似，在鳍运动区域周围有两层网格加密，第一层加密区的网格尺寸为0.05 m，第二层加密区的网格尺寸为0.1 m，背景区域的网格尺寸为0.2 m，总网格数量合计为10.6万。

利用尾鳍处最大速度Umax=0.934 m/s 来计算升力系数CL、力矩系数CM=3Fd/（4ρU2C）和Re，则Re=3×106，因此模拟采用SSTk-ω湍流模型。满足库朗数CFL=（U·Δt/Δx）＜1[14-15]，速度变量U取值Umax，Δx为最小网格尺寸0.05 m，计算合理的时间步长范围Δt＜0.54 s，确定时间步长为0.05 s。

对减摇鳍进行运动模拟，并将模拟结果与Wang 等[16]文献中的结果进行对比，如图6所示。

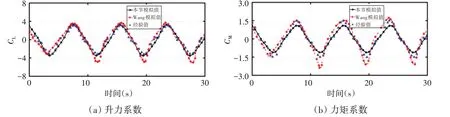
图6 模拟值和经验值的对比Fig.6 Comparison of simulated values and empirical values

观察图6可知，数值模拟的水动力系数与Wang等[16]文献中的模拟值和经验值非常接近，力矩系数则在总体趋势上比较一致，但在极值附近存在较大差异。主要原因是当减摇鳍在极值位置突然反向运动时，与周围流体形成巨大的速度差，产生流动分离和旋涡脱落等复杂现象，从而使鳍的形状力、旋涡力和附加质量力的计算变得比较困难[16]。另外，高雷诺数下的湍流模型给计算带来许多不确定因素[17]。

3 零航速船舶减横摇运动模拟

3.1 计算域及时间步长确定

对某船模的横摇运动进行模拟，其基本尺度如表1所示。

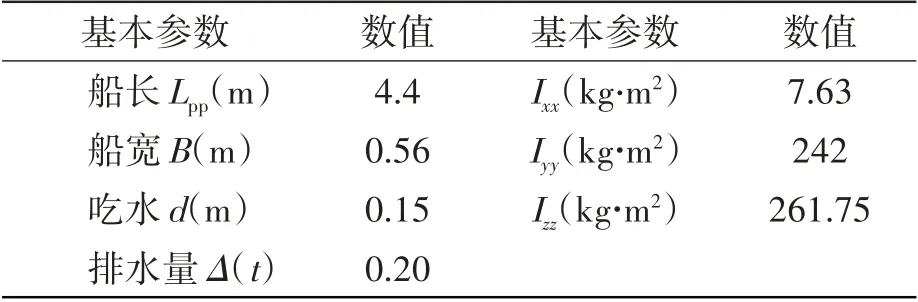
表1 船模的基本尺度Tab.1 Principal dimensions of ship model

计算域中，船模的船长方向与大地坐标系的Y轴平行，但仍与其随体坐标系中的X轴平行（如图7所示）。计算区域根据模型船的船长来设置，分别为-3＜（x/Lpp）＜1.5、-1＜（y/Lpp）和-2＜（z/Lpp）＜1，坐标原点设置在水面船体中心处。采用重叠网格对船舶横摇运动进行模拟，需要设置一个包括船体的小长方体，长度为1.5倍船长，宽度为0.6倍船长，高度为1倍船长。

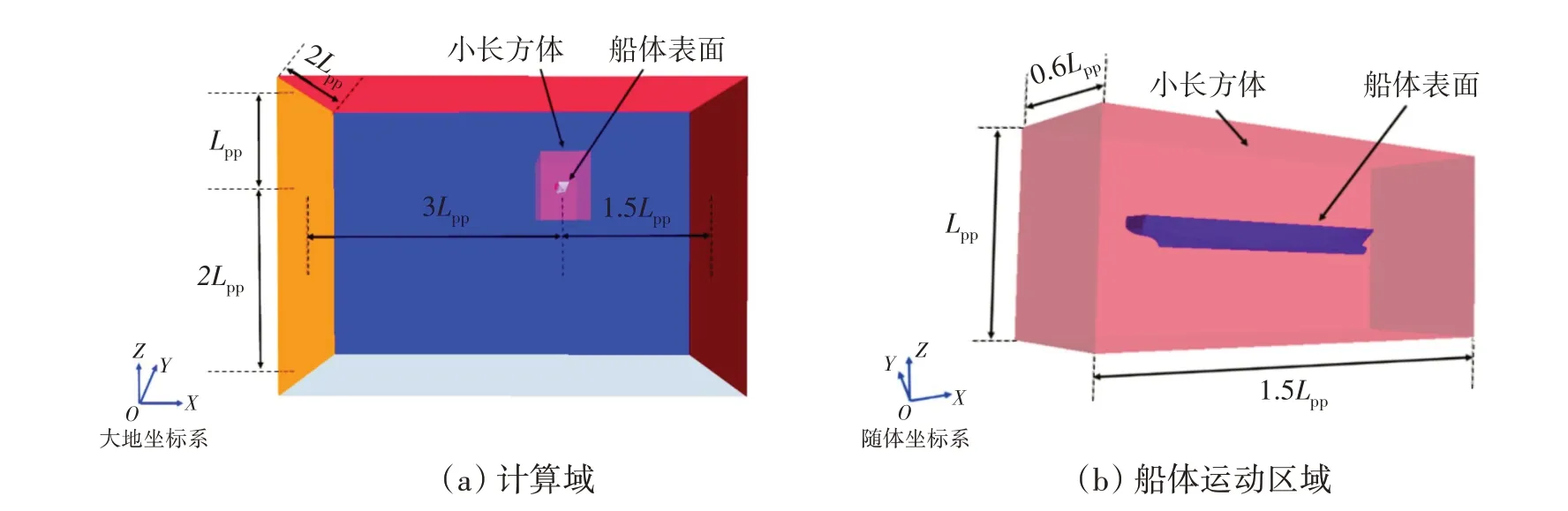
图7 计算域及船体运动区域Fig.7 Computational domain and ship motion region

计算域的边界条件设置如图8 所示：入口处对应入射波0.5H·sin（2πt/T1）的速度，其中，H为波高，T1为波浪周期；顶部速度为0；侧部为对称面；出口处设为压力出口，并采用阻尼消波的方式来防止波浪壁面反射；底部为非滑移壁面。

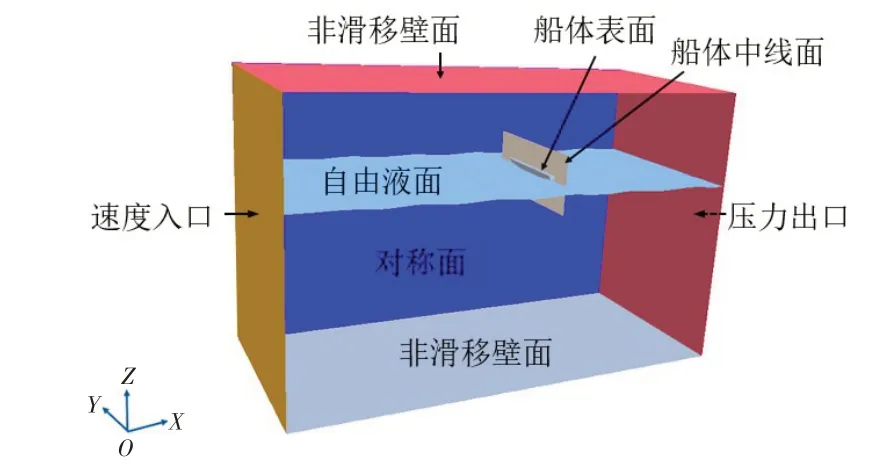
图8 横摇模拟计算域及边界条件Fig.8 Computational domain and boundary conditions in ship roll simulation

对船体近壁面、船体运动区域和自由液面附近的流场区域进行网格加密。图9为在中横剖面处，未安装减摇鳍的船舶网格分布图。背景区域的网格数量为70 万左右，船体运动区域的网格数量为117万左右，总网格数为187万左右。

图9 中横剖面处的网格分布图Fig.9 Grid distribution at the middle section

根据ITTC[18]对船舶耐波性计算案例的建议，本节对时间步长为0.005 s、0.002 5 s和0.00 125 s的横摇运动进行独立性验证。图10 显示的是船舶横摇稳定后，不同时间步长下船舶横摇角随时间变化的曲线图。可以发现，不同时间步长下横摇角、角速度和角加速度的幅值接近，说明所选择的时间步长对结果影响不大，计算结果收敛。综合考虑计算效率及波浪模拟的精度，后续计算的时间步长取为0.002 5 s。

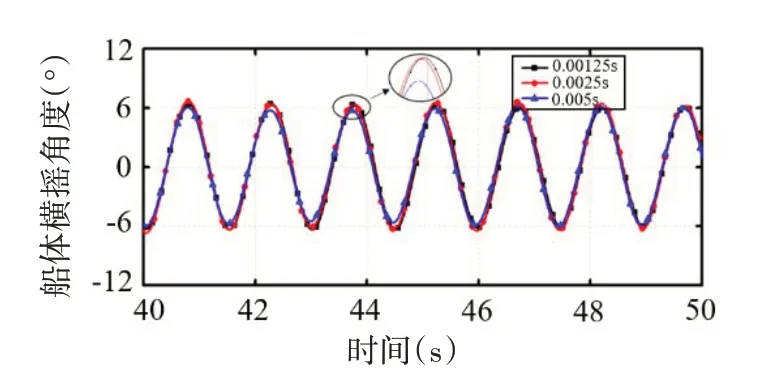
图10 船舶横摇运动时间步长独立性验证Fig.10 Independent verification of time step in ship rolling motion

3.2 船舶减横摇数值模拟

根据Dallinga 和Rapuc[4]的研究，当零航速减摇鳍的力矩和船舶横摇角速度存在相位差π 时，鳍的减摇效果最明显。国外研究人员曾做过有关鳍-船体适配性研究，试图探索减摇鳍和作六自由度运动船舶之间水动力的影响，发现减摇鳍性能的损失主要来自船体边界层的影响[9]；另外本文主要考虑零航速下的减摇鳍运动，静止船体对作简谐运动减摇鳍的水动力影响甚小。因此，假设零航速船体对减摇鳍运动水动力的影响可以忽略，那么确定鳍运动相位角的步骤为：对敞水条件下，作正弦运动的零航速减摇鳍进行数值模拟，获得鳍升力与鳍运动的相位差θ0，如图11所示；接着，数值模拟船舶在规则波作用下的横摇运动，使得鳍运动与船舶横摇角速度之间的相位差为θ0+π。

图11 减摇鳍转动角度与升力系数之间相位差Fig.11 Phase angle between fin stabilizer turning angle and lift coefficient

将一对零航速减摇鳍安装在船中舭部位置，鳍剖面为NACA 0020，弦长C=0.2 m，展长S=0.1 m，展弦比为0.5，鳍轴设置在距鳍前缘1/4位置处。减摇鳍的几何模型如图12所示：

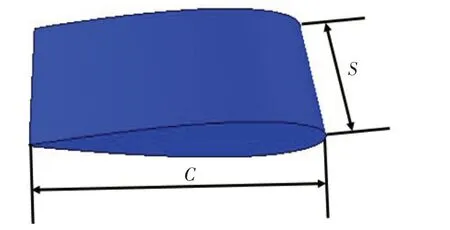
图12 鳍的几何模型Fig.12 Geometric model of fin

用无量纲的面积系数Cs来预估鳍和船体之间的几何大小关系，

式中，A1为安装在船体上所有减摇鳍的最大面积C×S之和，Lpp为船长，B为船宽。綦志刚[19]、Huang[20]和Ghassemi 等[21]的Cs分别为0.012、0.014 和0.01，本文采用的减摇鳍Cs=0.016，与其他文献的结果比较接近。根据船模对应实船航行时的要求，本计算取5 级海况下对应的模拟波高为0.08 m，并在4 个不同周期的规则波下进行减摇效率验证。

图13 为船舶横摇稳定后，CFD 模拟得到的无减摇鳍和安装减摇鳍的零航速船舶横摇角变化曲线比较。定义减摇效率η为

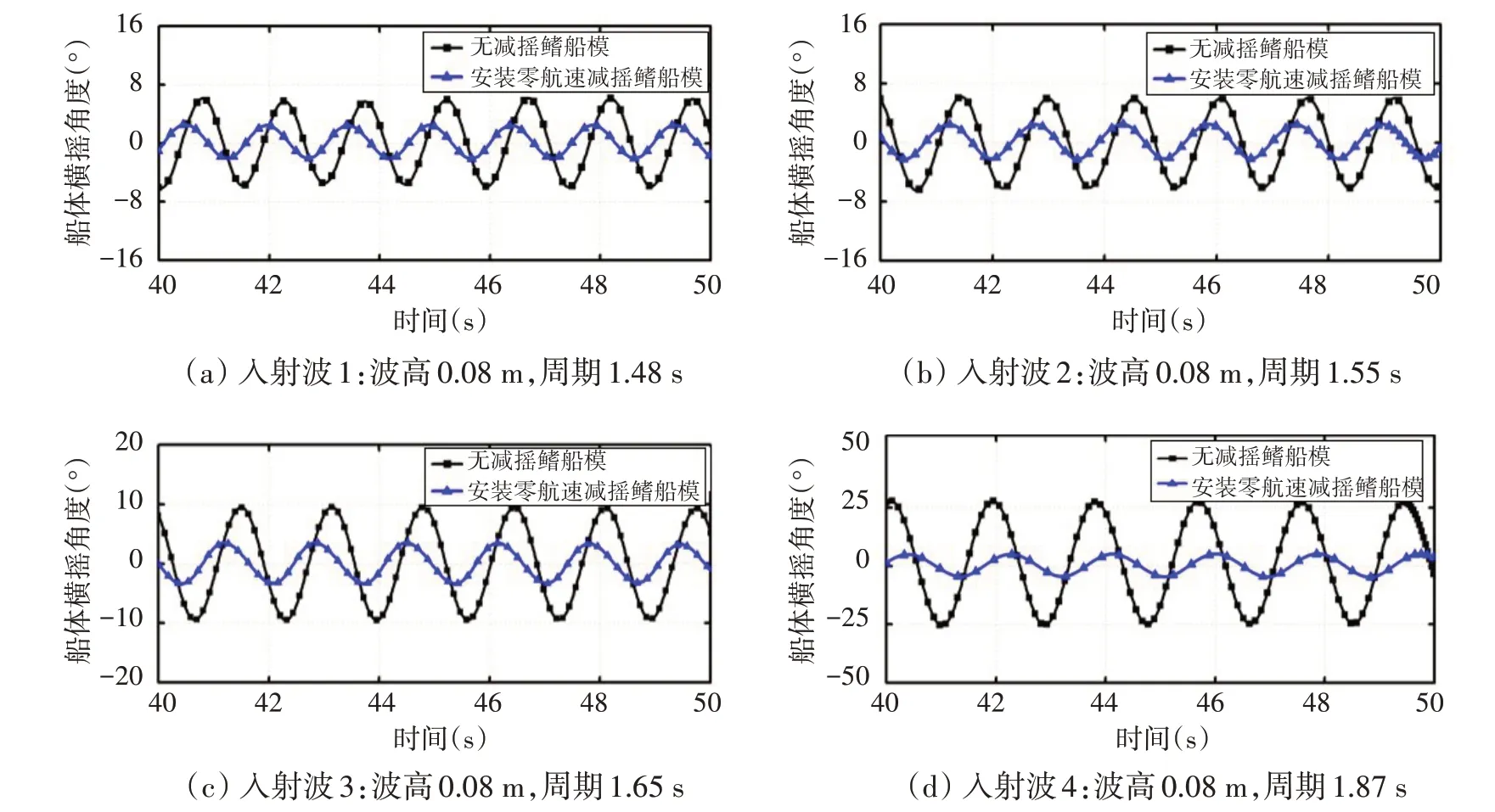
图13 无减摇鳍和安装减摇鳍的零航速船舶横摇角曲线Fig.13 Roll angle of ship at zero speed with and without fin stabilizer

式中，φ0和φ1分别为船舶横摇稳定时，未安装减摇鳍和安装零航速减摇鳍的船舶最大横摇角。则4个入射波条件下对应的鳍的减摇效率分别为61%、62%、63%和81%。

4 结 论

本文利用CFD软件，在数值模拟减摇鳍简单运动的基础上，分析得到减摇鳍运动与船舶横摇运动之间的关系，最后利用减摇鳍的主动简谐运动，对零航速船模在规则波中的横摇运动进行直接数值模拟，得出如下结论：

（1）在敞水条件下，对减摇鳍在有、无航速两种状态下作简谐运动时所受的流体动力进行数值计算，得到的结果与文献中的试验和数值计算结果比较吻合，为在复杂运动模式下的流体动力计算做好准备。

（2）利用零航速减摇鳍运动与船舶横摇运动之间的关系，对零航速船模在相同波高、4 个不同周期规则波下的横摇运动进行数值预报，发现减摇鳍的减摇效率在61%和81%之间，为进一步研究零航速船舶在不规则波下的减摇运动打下基础。